869d72036b8bcf8d623e5118f59788f8.ppt
- Количество слайдов: 42

Automated weather warning proposals based on post-processed numerical weather forecasts Guido Schröder, Bernhard Reichert, Dirk Heizenreder Deutscher Wetterdienst, Offenbach am Main, Germany 19 August 2014, WWOSC, Montreal, Canada
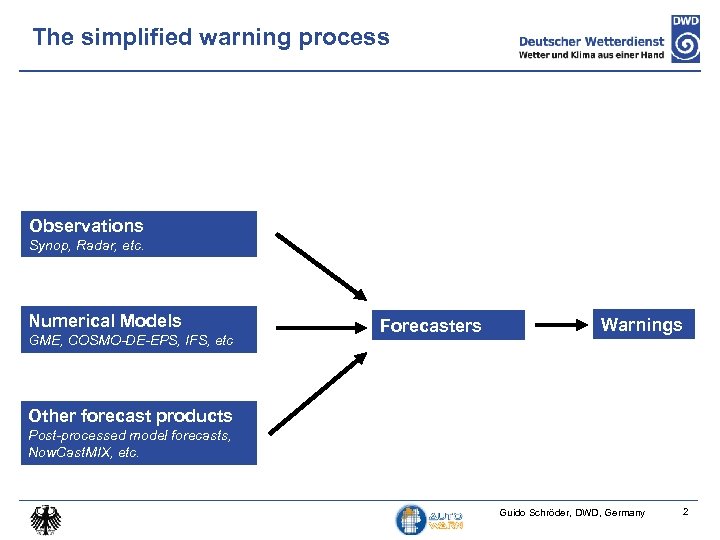
The simplified warning process Observations Synop, Radar, etc. Numerical Models GME, COSMO-DE-EPS, IFS, etc Forecasters Warnings Other forecast products Post-processed model forecasts, Now. Cast. MIX, etc. Guido Schröder, DWD, Germany 2

The simplified warning process with Auto. WARN Model. MIX Automated warnings Statistical Post-processing Observations Synop, Radar, etc. Numerical Models GME, COSMO-DE-EPS, IFS, etc. Forecasters integrate automated warnings Warnings Other forecast products Post-processed model forecasts, Now. Cast. MIX, etc. Guido Schröder, DWD, Germany 3

1) On the characteristics of weather warnings 2) Automatic generation of warning proposals 3) Verification with station observations 4) Summary and outlook Guido Schröder, DWD, Germany 4

1) On the characteristics of weather warnings 2) Automatic generation of warning proposals 3) Verification with station observations 4) Summary and outlook Guido Schröder, DWD, Germany 5
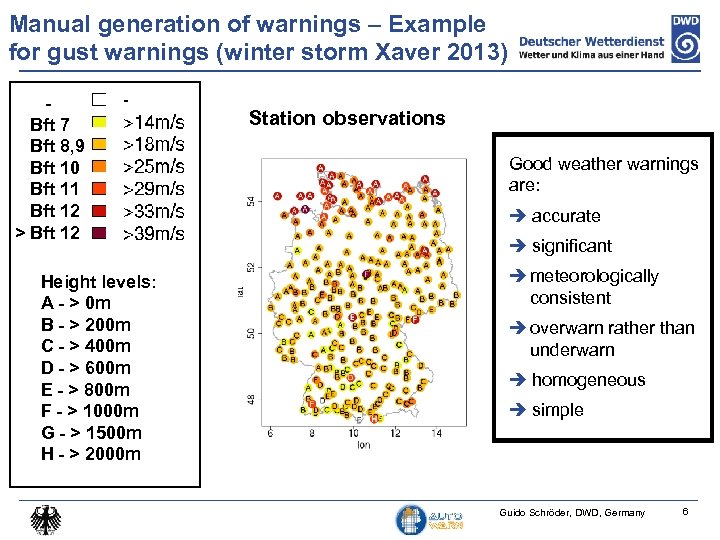
Manual generation of warnings – Example for gust warnings (winter storm Xaver 2013) Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Height levels: A - > 0 m B - > 200 m C - > 400 m D - > 600 m E - > 800 m F - > 1000 m G - > 1500 m H - > 2000 m Station observations Good weather warnings are: accurate significant meteorologically consistent overwarn rather than underwarn homogeneous simple Guido Schröder, DWD, Germany 6
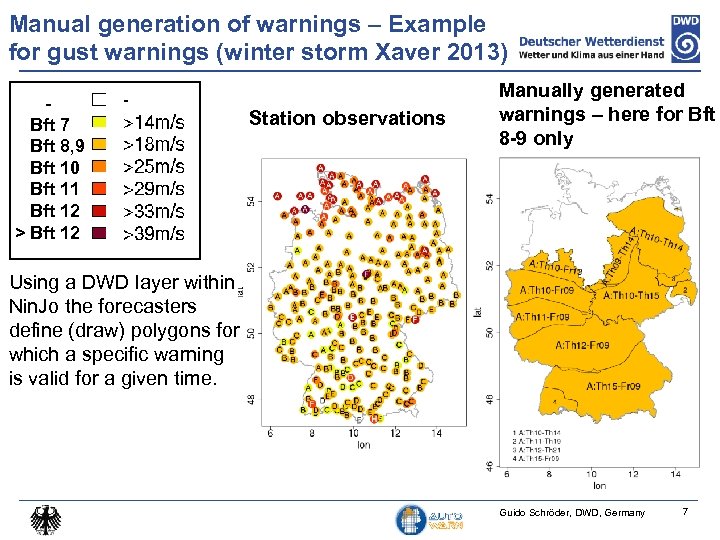
Manual generation of warnings – Example for gust warnings (winter storm Xaver 2013) Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Station observations Manually generated warnings – here for Bft 8 -9 only Using a DWD layer within Nin. Jo the forecasters define (draw) polygons for which a specific warning is valid for a given time. Guido Schröder, DWD, Germany 7
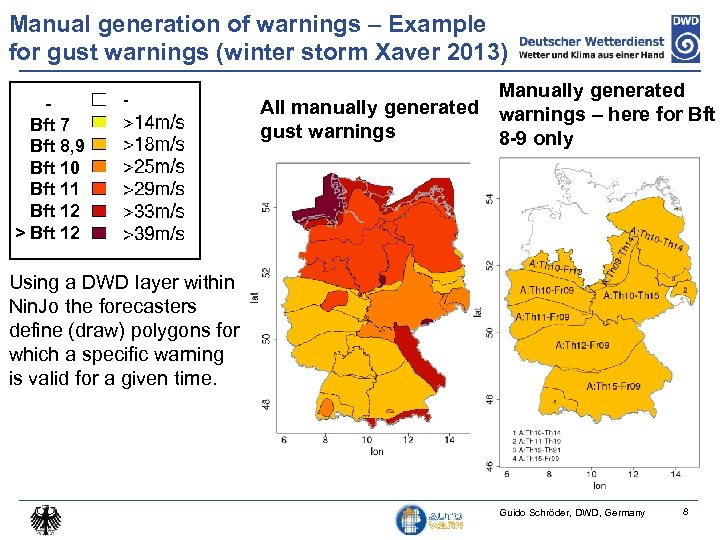
Manual generation of warnings – Example for gust warnings (winter storm Xaver 2013) Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Manually generated All manually generated warnings – here for Bft gust warnings 8 -9 only Using a DWD layer within Nin. Jo the forecasters define (draw) polygons for which a specific warning is valid for a given time. Guido Schröder, DWD, Germany 8
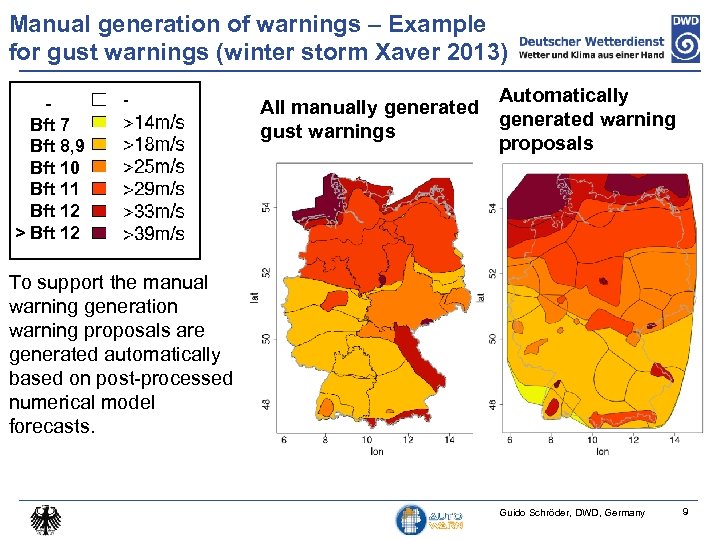
Manual generation of warnings – Example for gust warnings (winter storm Xaver 2013) Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Automatically All manually generated warning gust warnings proposals To support the manual warning generation warning proposals are generated automatically based on post-processed numerical model forecasts. Guido Schröder, DWD, Germany 9

1) On the characteristics of weather warnings 2) Automatic generation of warning proposals 3) Verification with station observations 4) Summary and outlook Guido Schröder, DWD, Germany 10
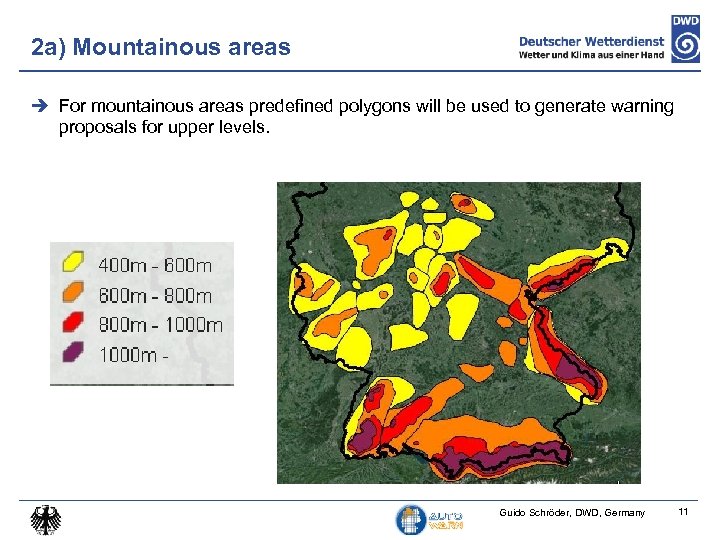
2 a) Mountainous areas For mountainous areas predefined polygons will be used to generate warning proposals for upper levels. Guido Schröder, DWD, Germany 11
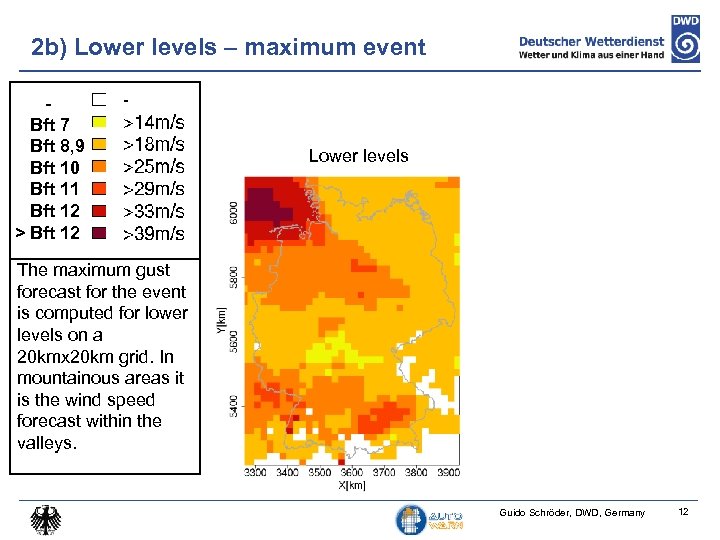
2 b) Lower levels – maximum event Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Lower levels The maximum gust forecast for the event is computed for lower levels on a 20 kmx 20 km grid. In mountainous areas it is the wind speed forecast within the valleys. Guido Schröder, DWD, Germany 12
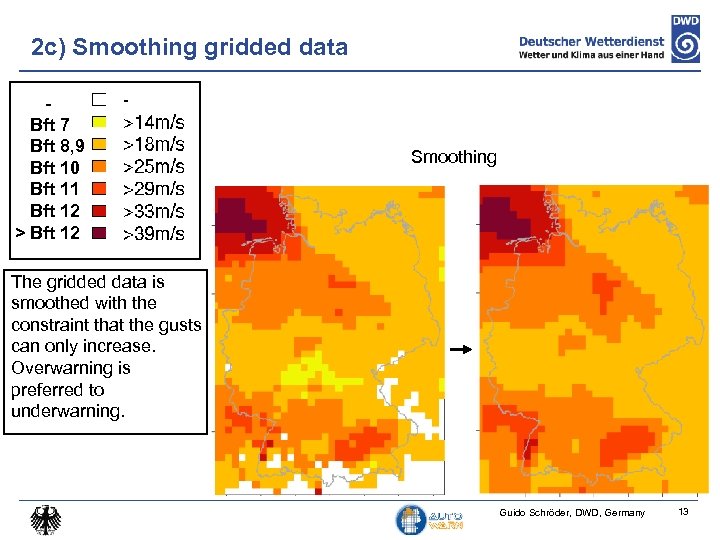
2 c) Smoothing gridded data Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Smoothing The gridded data is smoothed with the constraint that the gusts can only increase. Overwarning is preferred to underwarning. Guido Schröder, DWD, Germany 13
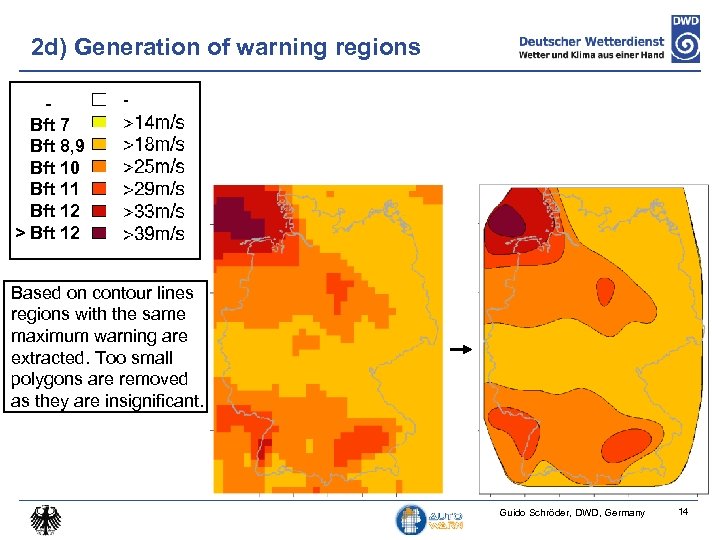
2 d) Generation of warning regions Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Based on contour lines regions with the same maximum warning are extracted. Too small polygons are removed as they are insignificant. Guido Schröder, DWD, Germany 14
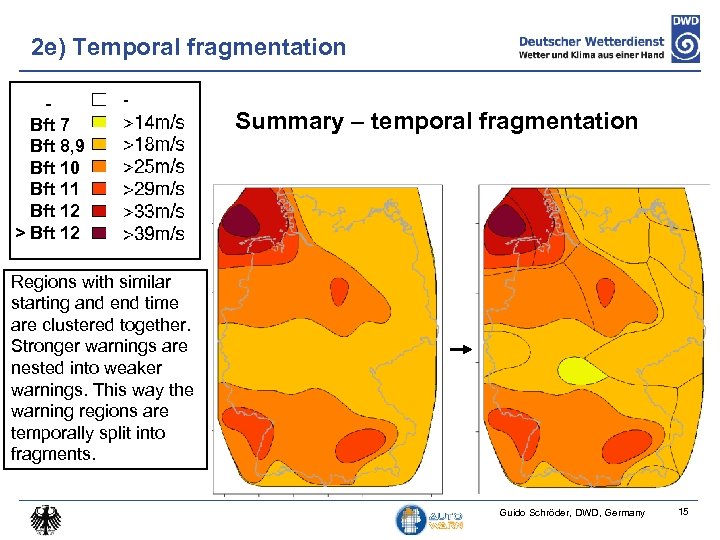
2 e) Temporal fragmentation Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Summary – temporal fragmentation Regions with similar starting and end time are clustered together. Stronger warnings are nested into weaker warnings. This way the warning regions are temporally split into fragments. Guido Schröder, DWD, Germany 15

1) On the characteristics of weather warnings 2) Automatic generation of warning proposals 3) Verification with station observations 4) Summary and outlook Guido Schröder, DWD, Germany 16
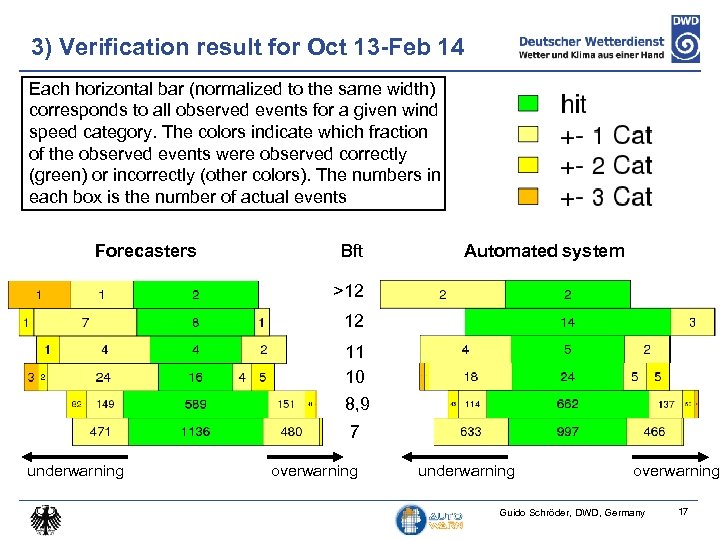
3) Verification result for Oct 13 -Feb 14 Each horizontal bar (normalized to the same width) corresponds to all observed events for a given wind speed category. The colors indicate which fraction of the observed events were observed correctly (green) or incorrectly (other colors). The numbers in each box is the number of actual events Forecasters Bft Automated system >12 12 11 10 8, 9 7 underwarning overwarning Guido Schröder, DWD, Germany 17

1) On the characteristics of weather warnings 2) Automatic generation of warning proposals 3) Verification with station observations 4) Summary and outlook Guido Schröder, DWD, Germany 18

4) Summary The increased amount of data in the warning process requires more and more automization The automated system tries to generate warning proposals the same way the forecaster would do it. That implies • Separate treatment of mountainous areas • Maximum of the event: It is more important to get the location right than the timing • Significance: Smoothing the gridded data The automated warnings give slightly better verification results than the manually generated warnings For low wind speeds (Bft 7) the automated system has the tendency to underwarn – the system needs to be optimized to generate automated warning at lower thresholds for Bft 7 Guido Schröder, DWD, Germany 19

4) Outlook For wind gusts the Auto. WARN system is already being tested Tools needs to be developed to better integrate the warning proposals into the actual warnings More research is needed in how to integrate several more numerical models (e. g. ICON, ICON-EPS, IFS-EPS) and data sources Probabilities for the events to occur need to be issued along with the warnings Guido Schröder, DWD, Germany 20

Appendix Guido Schröder, DWD, Germany 21

Strategic Goals of DWD for the Weather Warning Service DWD Strategy 2014 -2020: Development of a system for an optimal decision support in the warning process Automated support for the warning service and for the production of customer specific warn products Stepwise centralization of the warning service from current regional centers to the DWD headquarter in Offenbach Development of Auto. WARN: An automated decision support system with manual monitoring and decision capabilities for the forecaster Guido Schröder, DWD, Germany 22
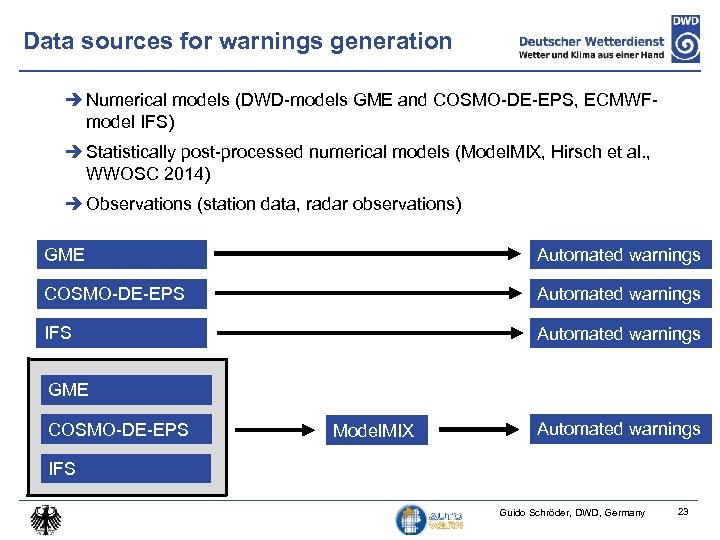
Data sources for warnings generation Numerical models (DWD-models GME and COSMO-DE-EPS, ECMWFmodel IFS) Statistically post-processed numerical models (Model. MIX, Hirsch et al. , WWOSC 2014) Observations (station data, radar observations) GME Automated warnings COSMO-DE-EPS Automated warnings IFS Automated warnings GME COSMO-DE-EPS Model. MIX Automated warnings IFS Guido Schröder, DWD, Germany 23
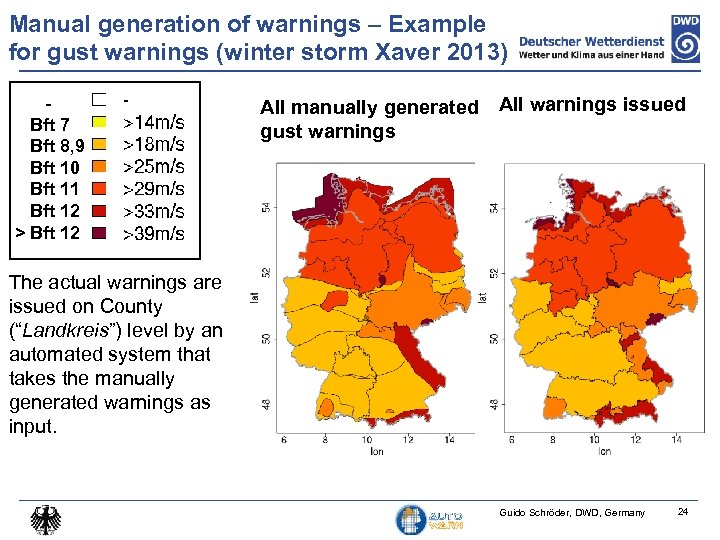
Manual generation of warnings – Example for gust warnings (winter storm Xaver 2013) Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 All manually generated All warnings issued gust warnings The actual warnings are issued on County (“Landkreis”) level by an automated system that takes the manually generated warnings as input. Guido Schröder, DWD, Germany 24
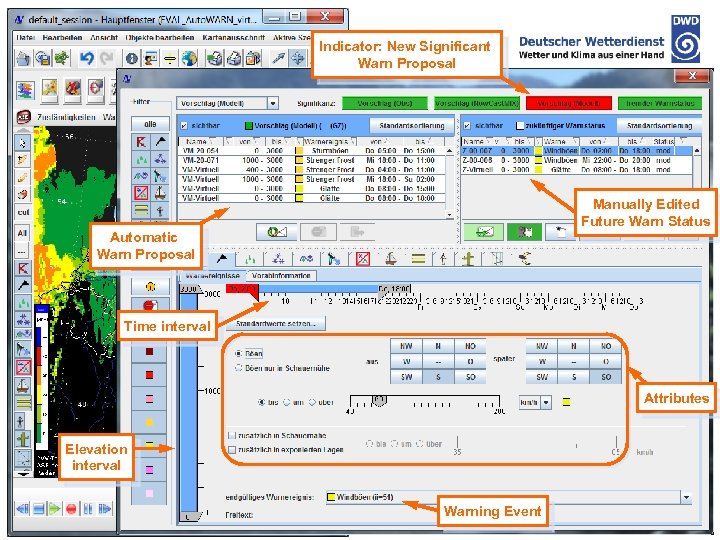
Indicator: New Significant Warn Proposal Manually Edited Future Warn Status Automatic Warn Proposal Time interval Attributes Elevation interval B. Reichert, FE ZE, DWD Warning Event
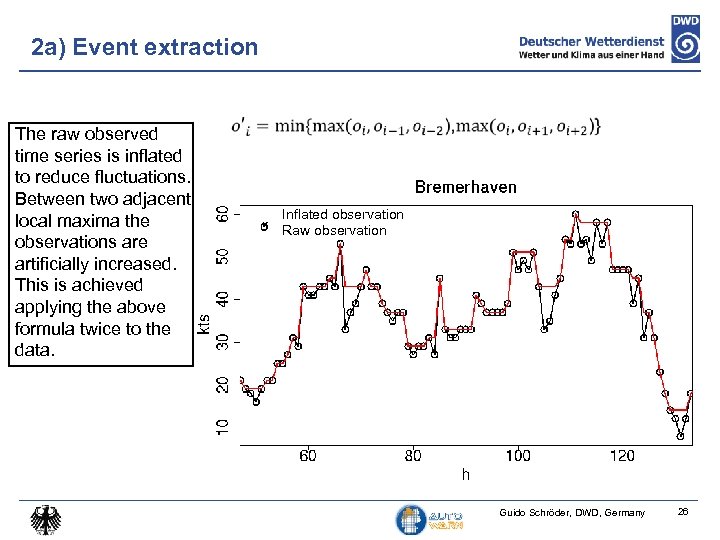
2 a) Event extraction The raw observed time series is inflated to reduce fluctuations. Between two adjacent local maxima the observations are artificially increased. This is achieved applying the above formula twice to the data. Inflated observation Raw observation Guido Schröder, DWD, Germany 26
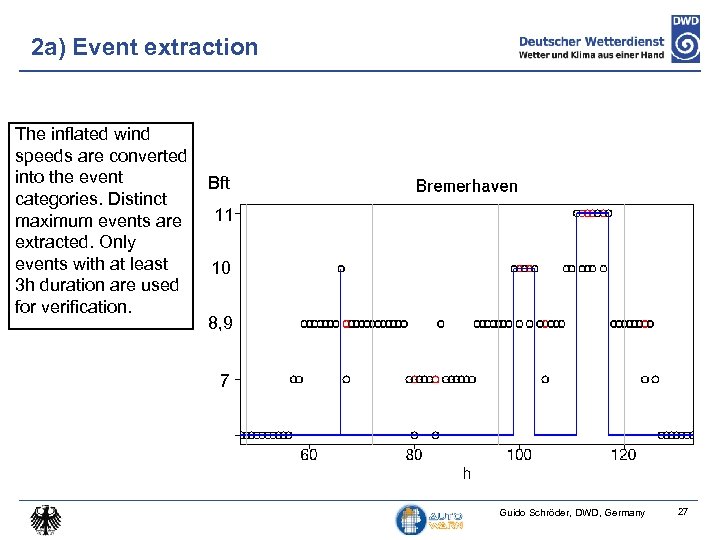
2 a) Event extraction The inflated wind speeds are converted into the event Bft categories. Distinct maximum events are 11 extracted. Only events with at least 10 3 h duration are used for verification. 8, 9 7 Guido Schröder, DWD, Germany 27
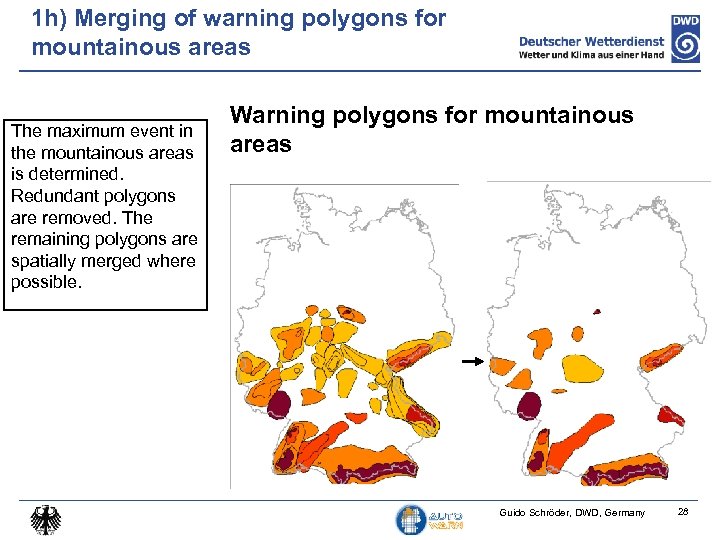
1 h) Merging of warning polygons for mountainous areas The maximum event in the mountainous areas is determined. Redundant polygons are removed. The remaining polygons are spatially merged where possible. Warning polygons for mountainous areas Guido Schröder, DWD, Germany 28

Appendix Smoothing Guido Schröder, FEZE-B, DWD 29

Filter for smoothing Higher order filters (Shapiro 1971, also Schlünzen et al. , 1996) 3 -Points 5 -Points 7 -Points Non-filtered value at grid point i Filtered value at grid point i
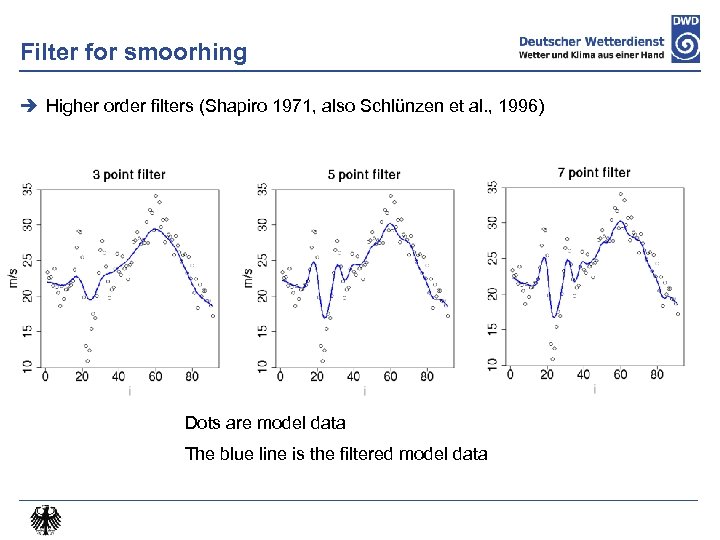
Filter for smoorhing Higher order filters (Shapiro 1971, also Schlünzen et al. , 1996) Dots are model data The blue line is the filtered model data

Multi-linear Regression for smoothing Assuming model values at , these can be approximated using a multilinear regression with the regression function where . Here where is generated as linear combination of with the coefficients The error is minimized. The base functions can be fields that describe the main structures in the data. It is impossible to attain a perfect fit everywhere – this is why a local regression is done – for each grid point with n surrounding grid points. For each grid point there are n values where k = 1, …, n. Of these a weighted average is computed while taking into account the error corresponding to the regression function. The smoothed value is then On this slide k and g are no exponents!
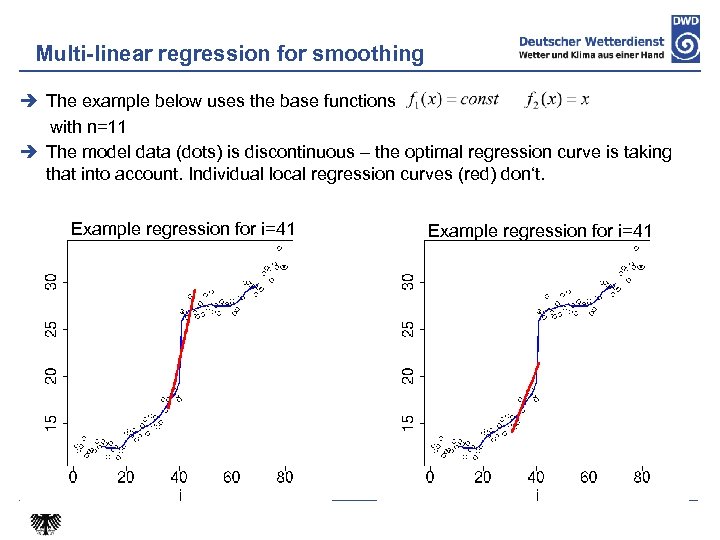
Multi-linear regression for smoothing The example below uses the base functions with n=11 The model data (dots) is discontinuous – the optimal regression curve is taking that into account. Individual local regression curves (red) don‘t. Example regression for i=41
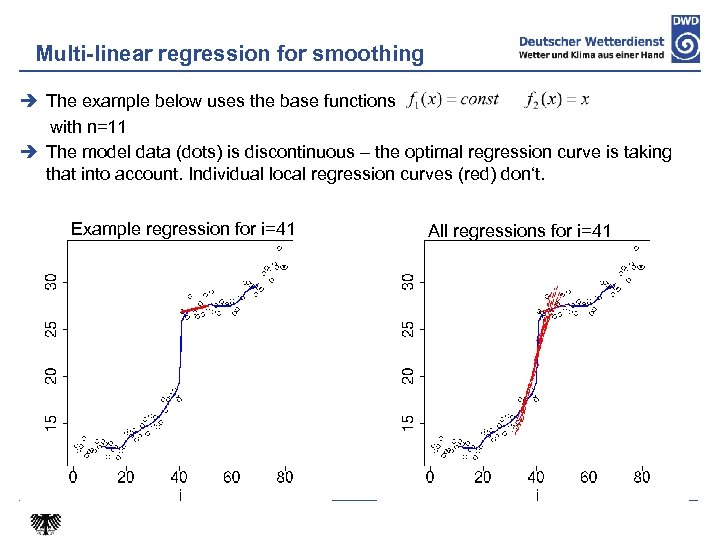
Multi-linear regression for smoothing The example below uses the base functions with n=11 The model data (dots) is discontinuous – the optimal regression curve is taking that into account. Individual local regression curves (red) don‘t. Example regression for i=41 All regressions for i=41
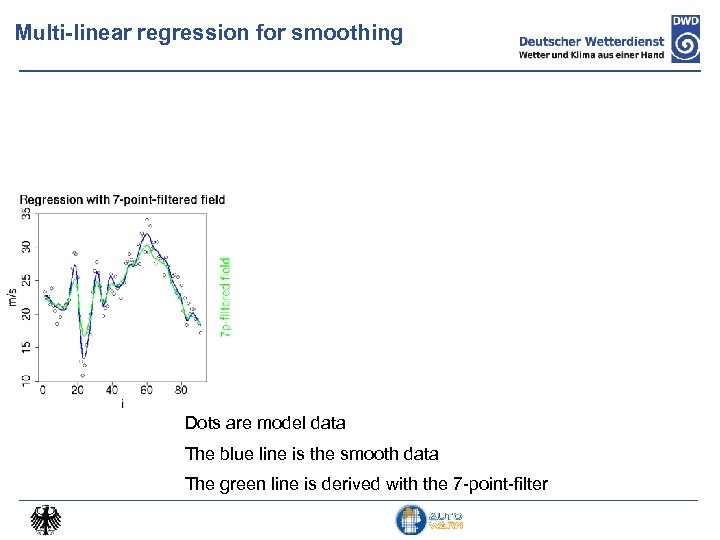
Multi-linear regression for smoothing Dots are model data The blue line is the smooth data The green line is derived with the 7 -point-filter

Quadratic programming for smoothing Multi-linear regression does not preserve maxima – which could mean that extreme warnings are smoothed away – which is not acceptable This problem can be solved by indroducing a constraint to the linear regression This is a quadratic programming problem and can be solved with standard solvers The above constraint ensures that all values can only increase. It is also possible to preserve only selected local maxima.
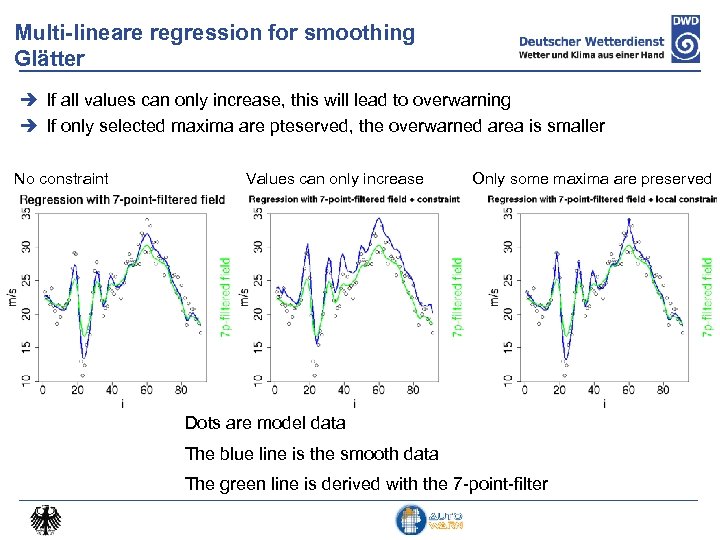
Multi-lineare regression for smoothing Glätter If all values can only increase, this will lead to overwarning If only selected maxima are pteserved, the overwarned area is smaller No constraint Values can only increase Only some maxima are preserved Dots are model data The blue line is the smooth data The green line is derived with the 7 -point-filter

Appendix temporal clustering Guido Schröder, FEZE-B, DWD 39
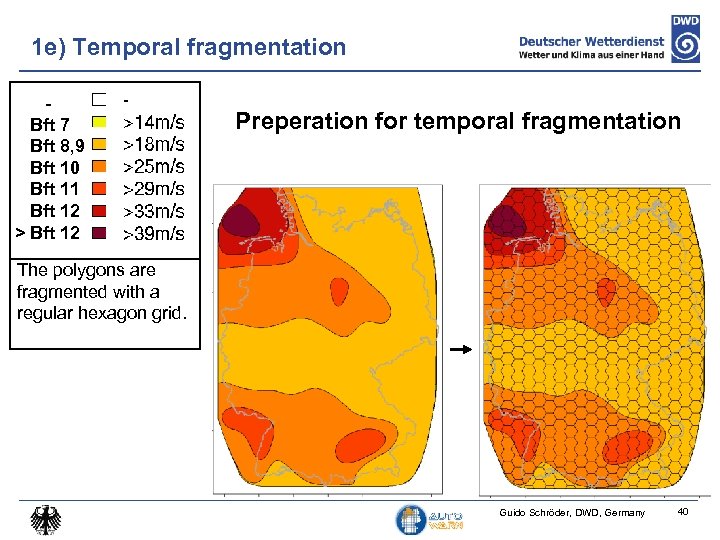
1 e) Temporal fragmentation Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Preperation for temporal fragmentation The polygons are fragmented with a regular hexagon grid. Guido Schröder, DWD, Germany 40
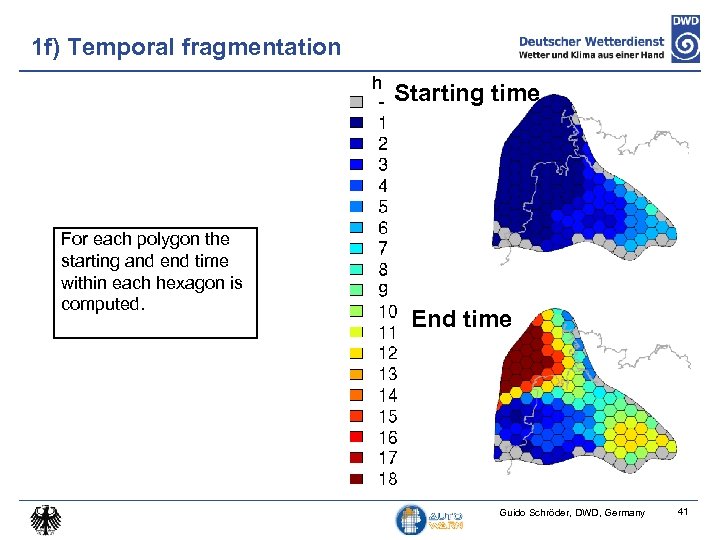
1 f) Temporal fragmentation h For each polygon the starting and end time within each hexagon is computed. Starting time End time Guido Schröder, DWD, Germany 41
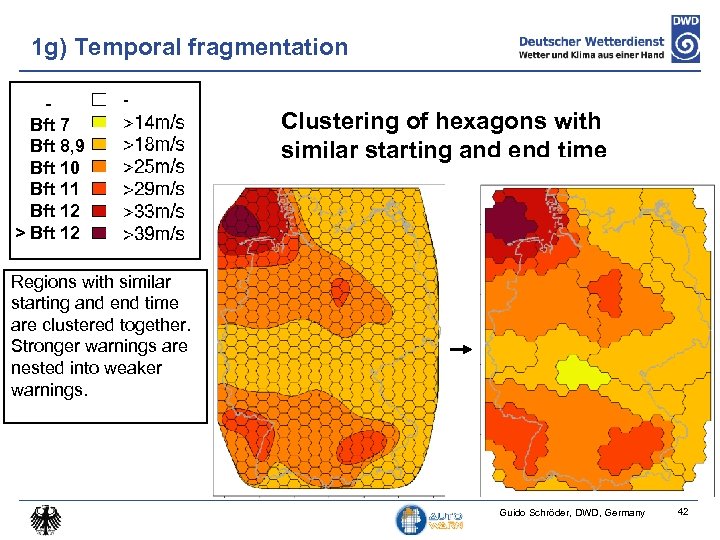
1 g) Temporal fragmentation Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Clustering of hexagons with similar starting and end time Regions with similar starting and end time are clustered together. Stronger warnings are nested into weaker warnings. Guido Schröder, DWD, Germany 42
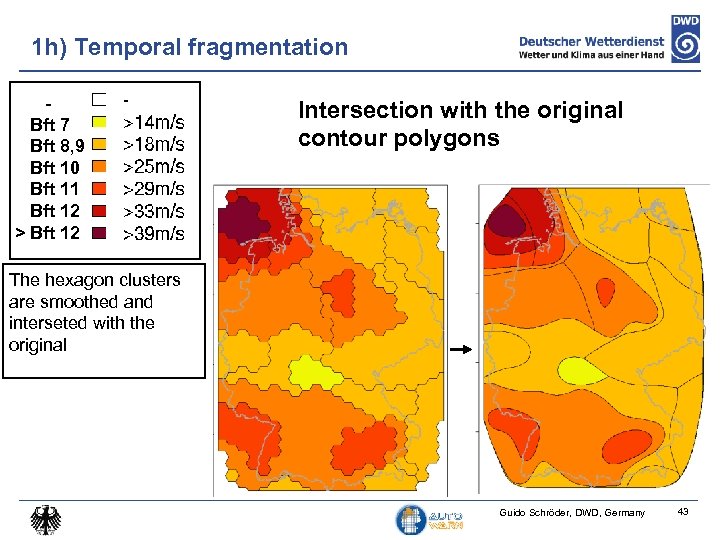
1 h) Temporal fragmentation Bft 7 Bft 8, 9 Bft 10 Bft 11 Bft 12 > Bft 12 Intersection with the original contour polygons The hexagon clusters are smoothed and interseted with the original Guido Schröder, DWD, Germany 43
869d72036b8bcf8d623e5118f59788f8.ppt