Automated Verification of Concurrent Linked Lists with Counters

Automated Verification of Concurrent Linked Lists with Counters Tuba Yavuz-Kahveci and Tevfik Bultan Department of Computer Science University of California, Santa Barbara {tuba, bultan}@cs. ucsb. edu http: //www. cs. ucsb. edu/~bultan/composite

General Problem n Concurrent programming is difficult and error prone – Sequential programming: states of the variables – Concurrent programming: states of the variables and the processes n Linked list manipulation is difficult and error prone – States of the heap: possibly infinite n We would like to guarantee properties of a concurrent linked list implementation

More Specific Problem n There has been work on verification of concurrent systems with integer variables (and linear constraints) – [Bultan, Gerber and Pugh, TOPLAS 99] – [Delzanno and Podelski STTT 01] – Use widening based on earlier work of [Cousot and Halbwachs POPL 77] on analyzing programs with integer variables n There has been work on verification of (concurrent) linked lists – [Yahav POPL’ 01] n What can we do for concurrent systems: – where both integer and heap variables influence the control flow, – or the properties we wish to verify involve both integer and heap variables?

Our Approach n Use symbolic verification techniques – Use polyhedra to represent the states of the integer variables – Use BDDs to represent the states of the boolean and enumerated variables – Use shape graphs to represent the states of the heap – Use composite representation to combine them n Use forward-fixpoint computations to compute reachable states – Truncated fixpoint computations can be used to detect errors – Over-approximation techniques can be used to prove properties • Polyhedra widening • Summarization in shape graphs

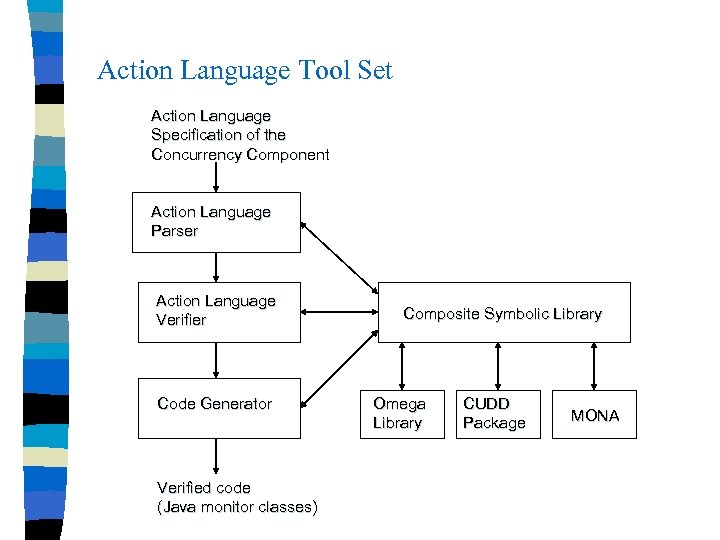Action Language Tool Set Action Language Specification of the Concurrency Component Action Language Parser Action Language Verifier Code Generator Verified code (Java monitor classes) Composite Symbolic Library Omega Library CUDD Package MONA

Outline n Specification of concurrent linked lists – Action Language n Symbolic verification – Composite representation n Approximation techniques – Summarization – Widening Counting abstraction n Experimental results n Related Work n Conclusions n

Action Language [Bultan ICSE 00] [Yavuz-Kahveci, Bultan ASE 01] n A state based language – Actions correspond to state changes n States correspond to valuations of variables – Integer (possibly unbounded), heap, boolean and enumerated variables – Parameterized constants are allowed n Transition relation is defined using actions – Atomic actions: Predicates on current and next state variables – Action composition: synchronous (&) or asynchronous (|) n Modular – Modules can have submodules n Properties to be verified – Invariant(p) : p always holds

Composite Formulas: State Formulas n We use state formulas to express the properties we need to check – No primed variables in state formulas – State formulas are boolean combination ( , , , , ) of integer, boolean and heap formulas num. Items>2 => top. next!=null integer formula heap formula

State formulas n Boolean formulas – Boolean variables and constants (true, false) – Relational operators: =, – Boolean connectives ( , , , , ) n Integer formulas (linear arithmetic) – – n Integer variables and constants Arithmetic operators: +, -, and * with a constant Relational operators: =, , > , <, , Boolean connectives ( , , , , ) Heap formulas – Heap variable, heap-variable. selector, heap constant null – Relational operators: =, – Boolean connectives ( , , , , )

Composite Formulas: Transition Formulas n We use transition formulas to express the actions – In transition formulas primed-variables denote the next-state values, unprimed-variables denote the current-sate values current state variables pc=checknull and num. Items=0 and top’=add and add’. next=null and num. Items’=1 and pc’=create and mutex’; next state variables

Transition Formulas n Transition formulas are in the form: boolean-formula integer-formula heap-transition-formula n Heap transition formulas are in the form: guard-formula update-formula n A guard formula is a conjunction of terms in the form: id 1 = id 2 id 1. f = id 2. f id 1 = null id 1. f = null n id 1 id 2 id 1. f id 2. f id 1 null id 1. f null An update formula is a conjunction of terms in the form: id’ 1 = id 2 id’ 1. f = id 2 id’ 1 = null id’ 1= new id’ 1 = id 2. f id’ 1. f = null id’ 1. f = new

Stack Example Variable declarations define the state space of the system module main() heap {next} top, add, get, new. Top; boolean mutex; integer num. Items; Predicates defining the initial states initial: top=null and mutex and num. Items=0; module push() Atomic actions: primed enumerated pc {create, checknull, update. Top}; variables denote next sate variables initial: pc=create and add=null; push 1: pc=create and mutex and !mutex’ and add’=new and pc’=checknull; push 2: pc=checknull and top=null and top’=add and add’. next=null and num. Items'=1 and pc’=create and mutex’; push 3: pc=checknull and top!=null and add’. next=top and pc’=update. Top; push 4: pc=update. Top and top’=add and num. Items’=num. Items+1 and mutex’ and pc’=create; push: push 1 | push 2 | push 3 | push 4; endmodule Transition relation of the push module is defined as asynchronous composition of its atomic actions

Stack (Cont’d) module pop() enumerated pc {copy. Top. Next, get. Top, update. Top}; initial: pc=copy. Top. Next and get=null and new. Top=null; pop 1: pc=copy. Top. Next and mutex and top!=null and new. Top’=top. next and !mutex’ and pc’=get. Top; pop 2: pc=get. Top and get’=top and pc’=update. Top; pop 3: pc=update. Top and top’=new. Top and mutex’ and num. Items’=num. Items-1 and pc’=copy. Top. Next; pop: pop 1 | pop 2 | pop 3; endmodule main: pop() | push(); spec: invariant([num. Items=0 => top=null]) spec: invariant([num. Items>2 => top->next!=null]) endmodule Invariants to be verified Transition relation of main defined as asynchronous composition of two pop and two push processes

Stack (with integer guards) module main() heap {next} top, add, get, new. Top; boolean mutex; integer num. Items; initial: top=null and mutex and num. Items=0; module push() enumerated pc {create, checknull, update. Top}; initial: pc=create and add=null; push 1: pc=create and mutex and !mutex’ and add’=new and pc’=checknull; push 2: pc=checknull and num. Items=0 and top’=add and add’. next=null and num. Items’=1 and pc’=create and mutex’; push 3: pc=checknull and num. Items>0 and add’. next=top and pc’=update. Top; push 4: pc=update. Top and top’=add and num. Items’=num. Items+1 and mutex’ and pc’=create; push: push 1 | push 2 | push 3 | push 4; endmodule

Outline n Specification of concurrent linked lists – Action Language n Symbolic verification – Composite representation n Approximation techniques – Summarization – Widening Counting abstraction n Experimental results n Related Work n Conclusions n

Symbolic Verification: Forward Fixpoint n Forward fixpoint for the reachable states can be computed by iteratively manipulating symbolic representations – We need forward-image (post-condition), union, and equivalence check computations Reachable. States(I: T: RS : = I; repeat { RSold : = RS; RS : = RSold } until (RSold = } Set of initial states, Transition relation) { forward. Image(RSold, T); RS)

Symbolic Verification: Symbolic Representations n Use a symbolic representation for the sets of states – A boolean logic formula (stored as a BDD) represents the sets of states of the boolean variables: pc=create mutex – An arithmetic constraint (stored as polyhedra) represents the sets of states of integer variables: num. Items>0 – Shape graphs are used to represent the sates of the heap variables and the heap add top

Composite Representation n Each variable type is mapped to a symbolic representation type – Boolean and enumerated types BDD representation – Integer variables Polyhedra – Heap variables Shape graphs Each conjunct in a transition formula operates on a single symbolic representation n Composite representation: A disjunctive representation to combine different symbolic representations n Union, equivalence check and forward-image computations are performed on this disjunctive representation n

Composite Representation n A composite representation A is a disjunction where – n is the number of composite atoms in A – t is the number of basic symbolic representations n Each composite atom is a conjunction – Each conjunct corresponds to a different symbolic representation

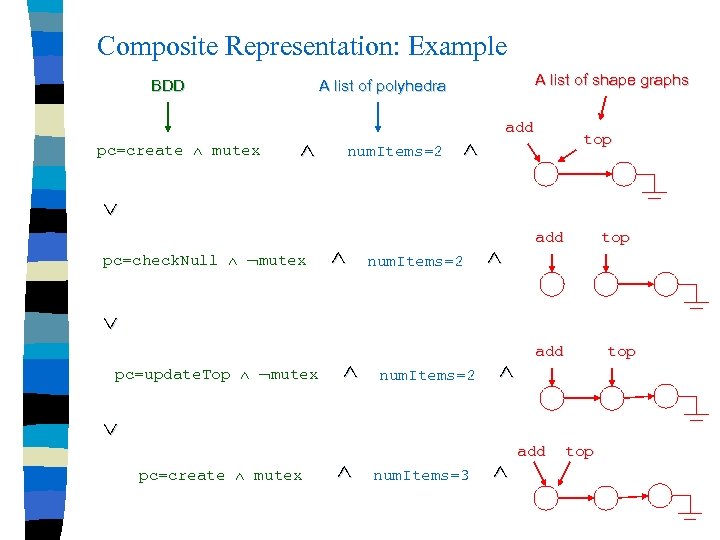Composite Representation: Example BDD pc=create mutex A list of shape graphs A list of polyhedra num. Items=2 add top pc=check. Null mutex num. Items=2 add top pc=update. Top mutex num. Items=2 add top pc=create mutex num. Items=3 add top

Composite Symbolic Library [Yavuz-Kahveci, Tuncer, Bultan TACAS 01], [Yavuz-Kahveci, Bultan STTT 02] n Our library implements this approach using an object-oriented design – A common interface is used for each symbolic representation – Easy to extend with new symbolic representations – Enables polymorphic verification – As a BDD library we use Colorado University Decision Diagram Package (CUDD) [Somenzi et al] – As an integer constraint manipulator we use Omega Library [Pugh et al] – For encoding the states of the heap variables and the heap we use shape graphs encoded as BDDs (using CUDD)

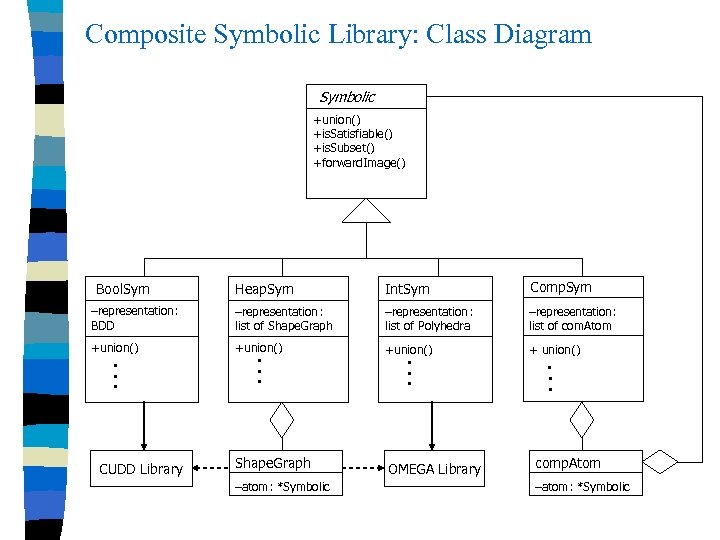Composite Symbolic Library: Class Diagram Symbolic +union() +is. Satisfiable() +is. Subset() +forward. Image() Heap. Sym Int. Sym Comp. Sym –representation: BDD –representation: list of Shape. Graph –representation: list of Polyhedra –representation: list of com. Atom +union() + union() Bool. Sym • • • CUDD Library • • • Shape. Graph –atom: *Symbolic • • • OMEGA Library • • • comp. Atom –atom: *Symbolic

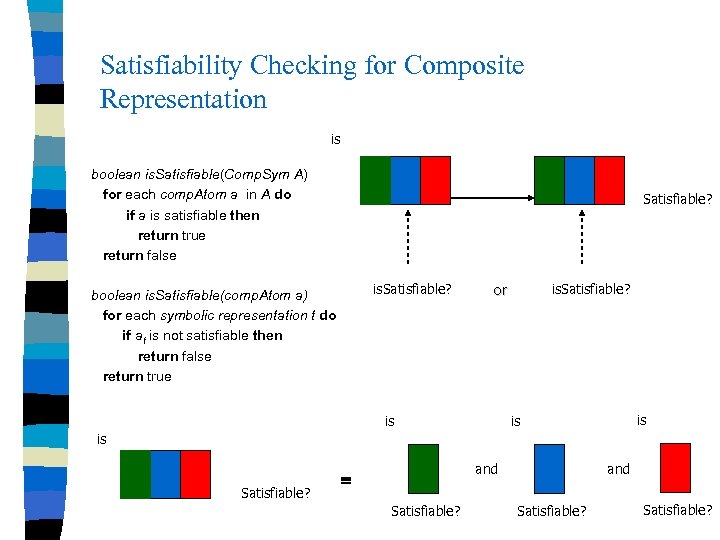Satisfiability Checking for Composite Representation is boolean is. Satisfiable(Comp. Sym A) for each comp. Atom a in A do if a is satisfiable then return true return false Satisfiable? is. Satisfiable? boolean is. Satisfiable(comp. Atom a) for each symbolic representation t do if at is not satisfiable then return false return true is. Satisfiable? or is is Satisfiable? and Satisfiable?

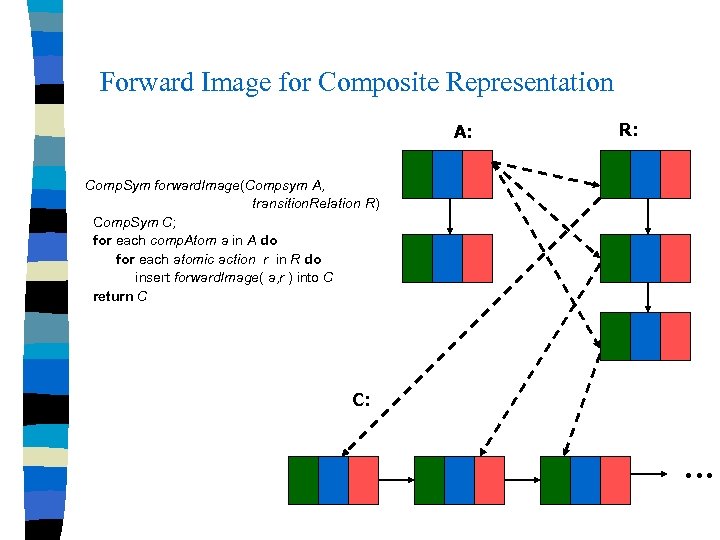Forward Image for Composite Representation A: R: Comp. Sym forward. Image(Compsym A, transition. Relation R) Comp. Sym C; for each comp. Atom a in A do for each atomic action r in R do insert forward. Image( a, r ) into C return C C: • • •

Forward Image for Composite Atom comp. Atom forward. Image(comp. Atom a, atomic action r) for each symbolic representation type t do replace at by forward. Image(at , rt ) return a r: a:

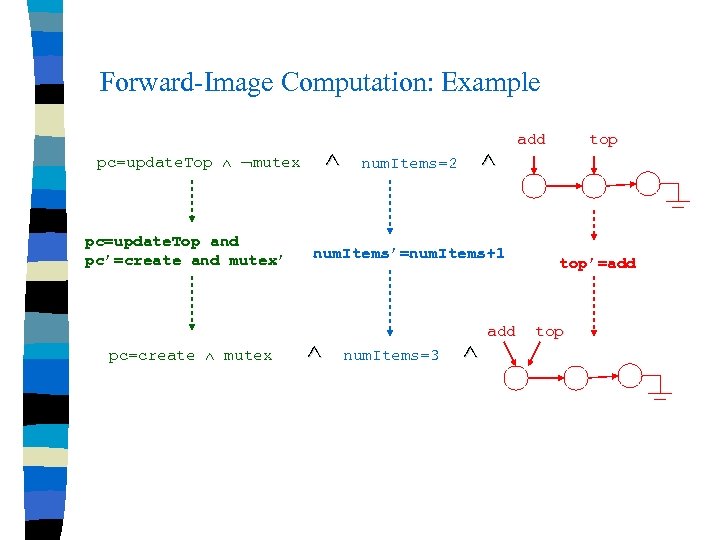Forward-Image Computation: Example pc=update. Top mutex pc=update. Top and pc’=create and mutex’ pc=create mutex num. Items=2 num. Items’=num. Items+1 num. Items=3 add top’=add top

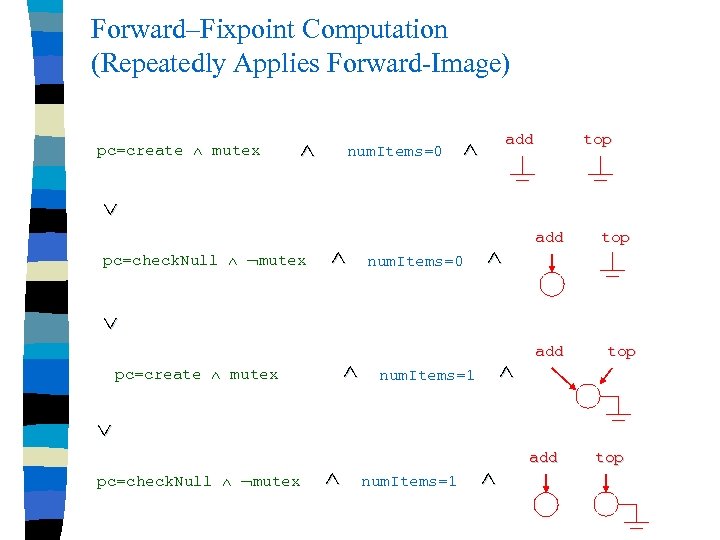Forward–Fixpoint Computation (Repeatedly Applies Forward-Image) pc=create mutex num. Items=0 add top pc=check. Null mutex num. Items=0 add top pc=create mutex num. Items=1 add top pc=check. Null mutex num. Items=1 add top

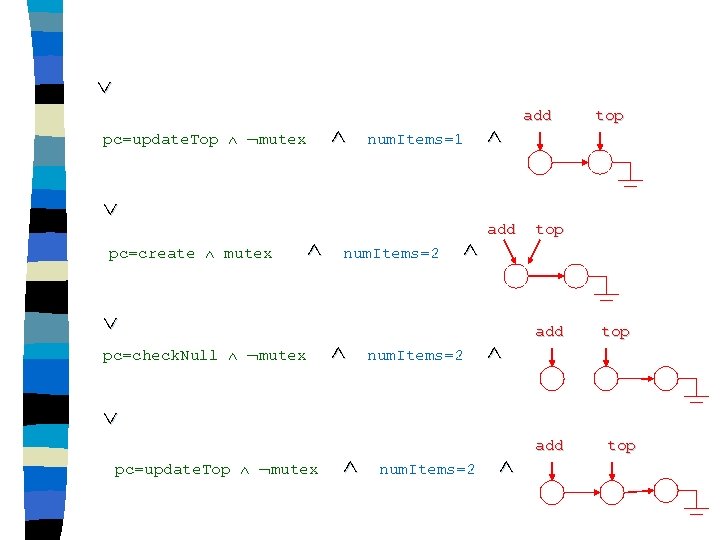pc=update. Top mutex num. Items=1 pc=create mutex pc=check. Null mutex num. Items=2 add top pc=update. Top mutex num. Items=2 add top

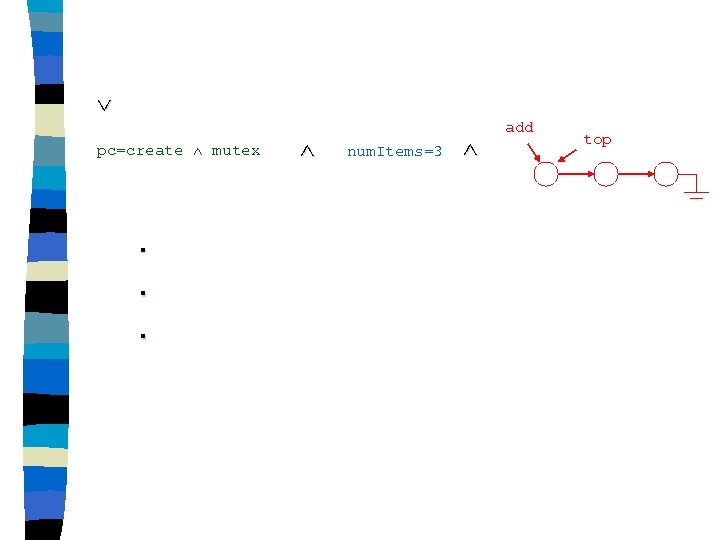pc=create mutex . . . num. Items=3 add top

Forward-Fixpoint does not Converge n We have two reasons for non-termination – integer variables can increase without a bound – the number of nodes in the shape graphs can increase without a bound The state space is infinite n Even if we ignore the heap variables, reachability is undecidable when we have unbounded integer variables n So, we use conservative approximations n

Outline n Specification of concurrent linked lists – Action Language n Symbolic verification – Composite representation n Approximation techniques – Summarization – Widening Counting Abstraction n Experimental results n Related Work n Conclusions n

Conservative Approximations n To verify or falsify a property p Compute a lower ( RS ) or an upper ( RS + ) approximation to the set of reachable states n There are three possibilities: n p RS “The property is satisfied” RS +

Conservative Approximations reachable sates which violate the property p RS “The property is false” p RS “I don’t know” RS RS +

Computing Upper and Lower Bounds for Reachable States n Truncated fixpoint computation – To compute a lower bound for a least-fixpoint computation – Stops after a fixed number of iterations n Widening – To compute an upper bound for the least-fixpoint computation – We use a generalization of the polyhedra widening operator by [Cousot and Halbwachs POPL’ 77] n Summarization – Generate heap nodes in the shape graphs which represent more than one concrete node – Materialization: we need to generate concrete nodes from the summary nodes when needed

Summarization n The nodes mapped to a summary node form a chain . . . No heap variable points to any concrete node that is mapped to a summary node n Each concrete node mapped to a summary node is only pointed by one pointer n During summarization, we also introduce an integer variable which counts the number of concrete nodes mapped to a summary node n

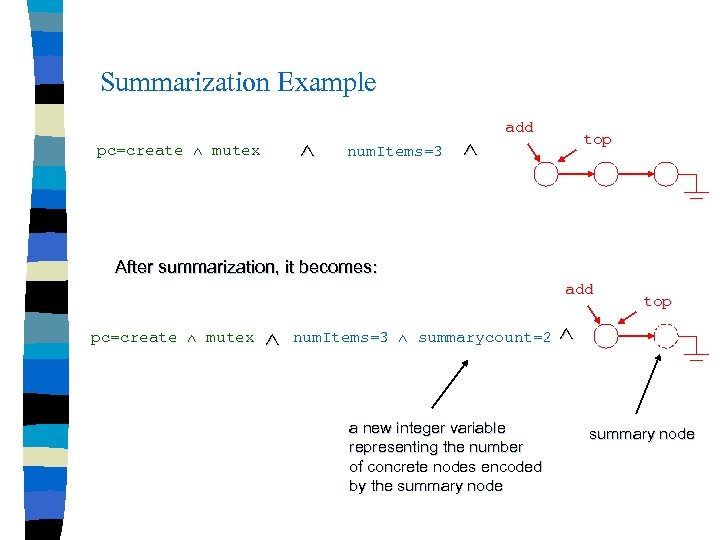Summarization Example pc=create mutex num. Items=3 add top After summarization, it becomes: add pc=create mutex num. Items=3 summarycount=2 a new integer variable representing the number of concrete nodes encoded by the summary node top summary node

Summarization guarantees that the number of different shape graphs that can be generated are finite n However, the summary-counts can still increase without a bound n We use polyhedral widening operation to force the fixpoint computation to convergence n

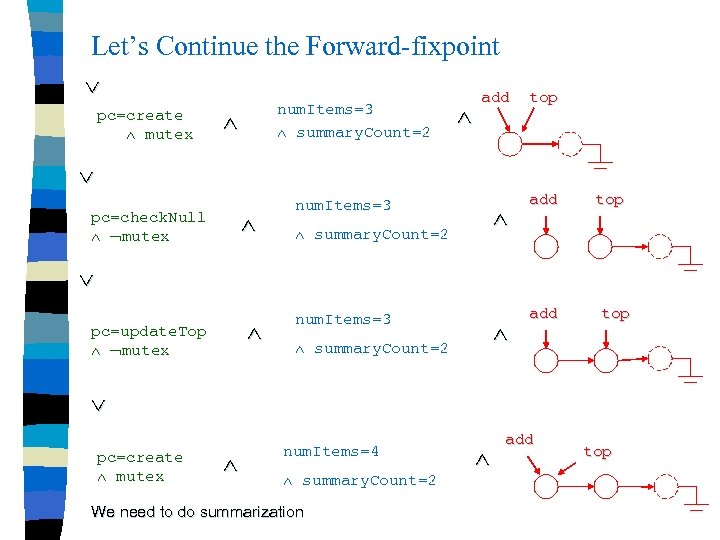Let’s Continue the Forward-fixpoint pc=create mutex num. Items=3 summary. Count=2 add top pc=check. Null mutex num. Items=3 summary. Count=2 add top pc=update. Top mutex num. Items=3 summary. Count=2 add top pc=create mutex num. Items=4 summary. Count=2 We need to do summarization add top

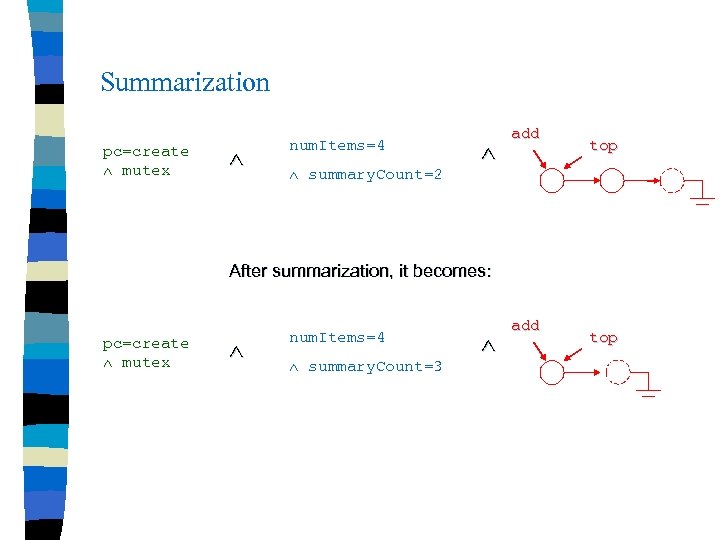Summarization pc=create mutex num. Items=4 summary. Count=2 add top After summarization, it becomes: pc=create mutex num. Items=4 summary. Count=3 add top

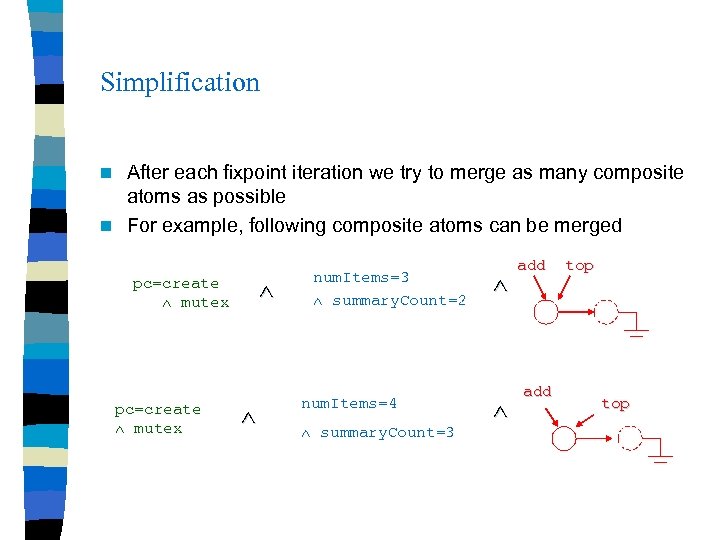Simplification After each fixpoint iteration we try to merge as many composite atoms as possible n For example, following composite atoms can be merged n pc=create mutex num. Items=3 summary. Count=2 num. Items=4 summary. Count=3 add top

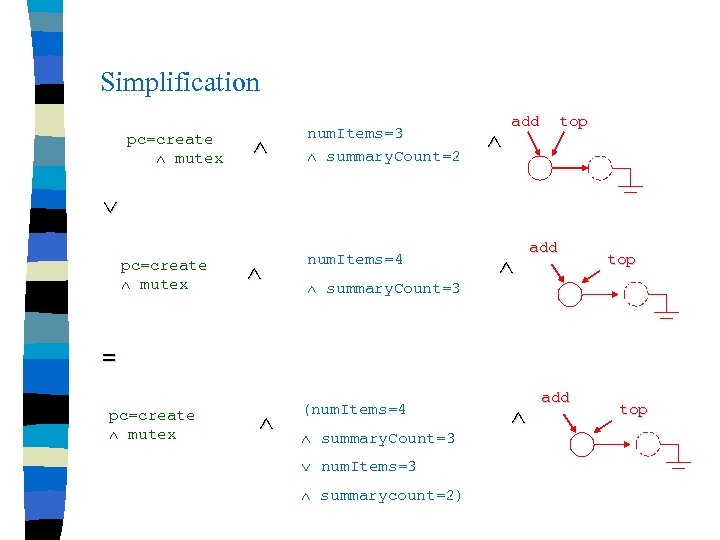Simplification pc=create mutex num. Items=3 summary. Count=2 add top pc=create mutex num. Items=4 summary. Count=3 add top = pc=create mutex (num. Items=4 summary. Count=3 num. Items=3 summarycount=2) add top

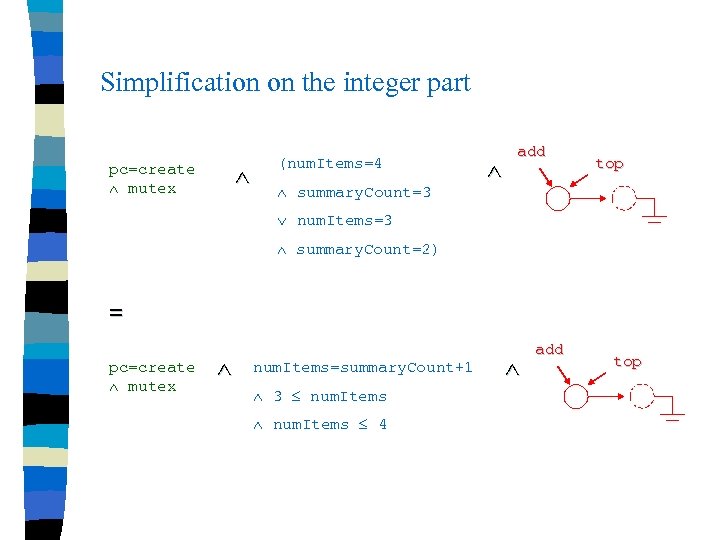Simplification on the integer part pc=create mutex (num. Items=4 summary. Count=3 add top num. Items=3 summary. Count=2) = pc=create mutex num. Items=summary. Count+1 3 num. Items 4 add top

Widening Forward-fixpoint computation still will not converge since num. Items and summary. Count keep increasing without a bound n We use the widening operation: n – Given two composite atoms c 1 and c 2 in consecutive fixpoint iterates, assume that c 1 = b 1 i 1 h 1 c 2 = b 2 i 2 h 2 where b 1 = b 2 and h 1 = h 2 and i 1 i 2 – Also assume that i 1 is a single polyhedron (i. e. a conjunction of arithmetic csontraints) and i 2 is also a single polyhedron

Widening n Then – i 1 i 2 is defined as: all the constraints in i 1 which are also satisfied by i 2 Replace i 2 with i 1 i 2 in c 2 n This gives a majorizing sequence to the forward-fixpoint computation n

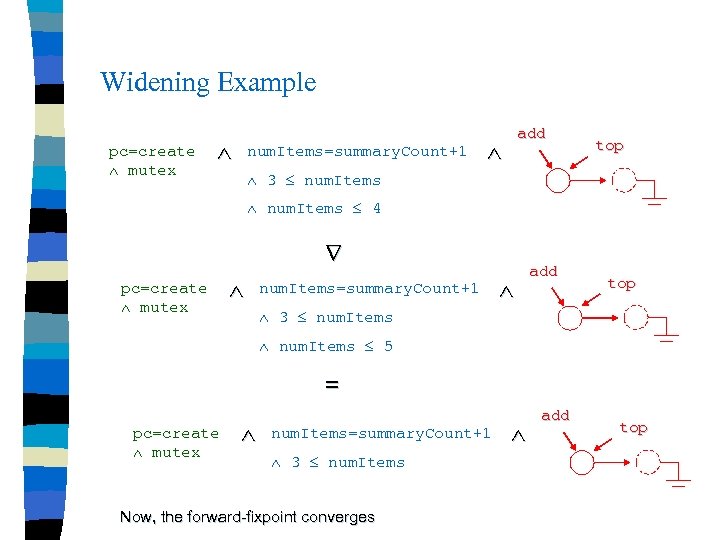Widening Example pc=create mutex num. Items=summary. Count+1 add top 3 num. Items 4 pc=create mutex num. Items=summary. Count+1 add top 3 num. Items 5 = pc=create mutex num. Items=summary. Count+1 3 num. Items Now, the forward-fixpoint converges add top

Dealing with Arbitrary Number of Processes n Use counting abstraction [Delzanno CAV’ 00] – Create an integer variable for each local state of a process – Each variable will count the number of processes in a particular state n Local states of the processes have to be finite – Shared variables of the monitor can be unbounded n Counting abstraction can be automated

Stack After Counting Abstraction Variables for counting the number of processes in each state module main() heap top, add, get, new. Top; Parameterized constant boolean mutex; representing the number of integer num. Items; processes integer Create. C, Checknull. C, Update. Top. C; parameterized integer num. Processes; initial: top=null and mutex and num. Items=0 and Initialize initial state counter Create. C=num. Processes and Checknull. C=0 and Update. Top. C=0; to the number of processes. restrict: num. Processes>0; Initialize other states to 0. module push() //enumerated pc {create, checknull, update. Top}; initial: add=null; push 1: Create. C>0 and mutex and !mutex' and add'=new and Create. C'=Create. C-1 and Checknull. C'=Checknull. C+1; push 2: Checknull. C>0 and top=null and top'=add and add'->next=null and num. Items'=1 and Checknull. C'=Checknull. C-1 and Create. C'=Create. C+1 and mutex'; push 3: Checknull. C>0 and top!=null and add'->next=top and Checknull. C'=Checknull. C-1 and Update. Top. C'=Update. Top. C+1; push 4: Update. Top. C>0 and top'=add and num. Items'=num. Items+1 and mutex' and Update. Top. C'=Update. Top. C-1 and Create. C'=Create. C+1; push: push 1 | push 2 | push 3 | push 4; When local state changes, endmodule decrement current local state counter and increment next local state counter

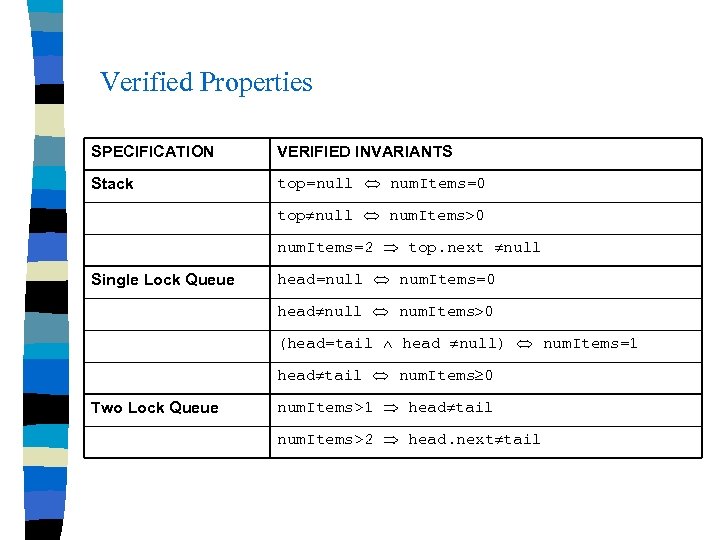Verified Properties SPECIFICATION VERIFIED INVARIANTS Stack top=null num. Items=0 top null num. Items 0 num. Items=2 top. next null Single Lock Queue head=null num. Items=0 head null num. Items 0 (head=tail head null) num. Items=1 head tail num. Items 0 Two Lock Queue num. Items>1 head tail num. Items>2 head. next tail

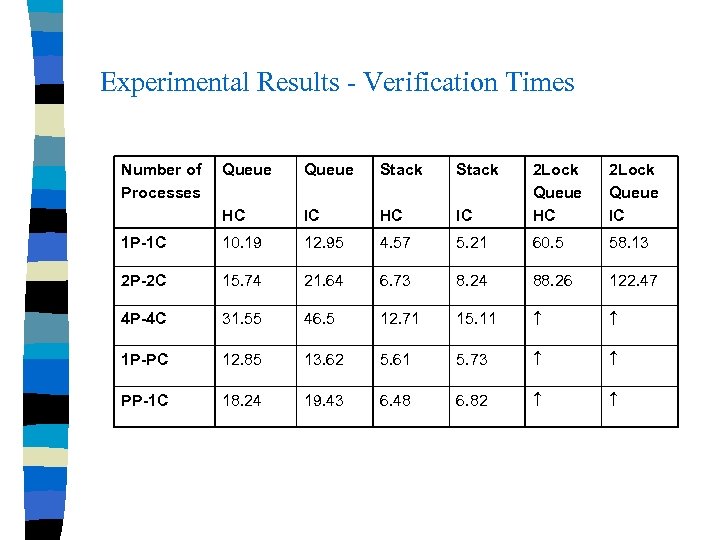Experimental Results - Verification Times Number of Processes Queue Stack IC 2 Lock Queue HC 2 Lock Queue IC HC 1 P-1 C 10. 19 12. 95 4. 57 5. 21 60. 5 58. 13 2 P-2 C 15. 74 21. 64 6. 73 8. 24 88. 26 122. 47 4 P-4 C 31. 55 46. 5 12. 71 15. 11 1 P-PC 12. 85 13. 62 5. 61 5. 73 PP-1 C 18. 24 19. 43 6. 48 6. 82

Related Work n There is a lot of work on Shape analysis, I will just mention the ones which directly influenced us: – [Sagiv, Reps, Wilhelm TOPLAS’ 98], [Dor, Rodeh, Sagiv SAS’ 00] Verification of concurrent linked lists with arbitrary number of processes in [Yahav POPL’ 01] n [Lev-Ami, Reps, Sagiv, Wilhelm ISSTA 00] use 3 -valued logic and instrumentation predicates to verify properties that cannot be expressed in our framework, however, our approach does not require instrumentation predicates n Deutch used integer constraint lattices to compute aliasing information using symbolic access paths [Deutch PLDI’ 94] n Use of BDDs goes back to symbolic model checking [Mc. Millan’ 93] and verification with arithmetic constraints goes back to [Cousot and Halbwachs’ 77] n

Conclusions and Future Work n One of the weakness of the summarization algorithm we used is the fact that it only works on singly linked lists – We need to find a more general summarizaton algorithm which counts the number of summary nodes Implementation is not efficient, we are working on improving the performance n Liveness properties? n – We would like to do full CTL model checking – Need to implement the backward image computation

APPENDIX

Action Language Verifier An infinite state symbolic model checker n Composite representation n – uses a disjunctive representation to combine different symbolic representations n Computes fixpoints by manipulating formulas in composite representation – Heuristics to ensure convergence • Widening & collapsing • Loop closure • Approximate reachable states

Readers Writers Monitor in Action Language module main() integer nr; boolean busy; restrict: nr>=0; initial: nr=0 and !busy; module Reader() boolean reading; initial: !reading; r. Enter: !reading and !busy and nr’=nr+1 and reading’; r. Exit: reading and !reading’ and nr’=nr-1; Reader: r. Enter | r. Exit; endmodule Writer() boolean writing; initial: !writing; w. Enter: !writing and nr=0 and !busy and busy’ and writing’; w. Exit: writing and !writing’ and !busy’; Writer: w. Enter | w. Exit; endmodule main: Reader() | Writer(); spec: invariant([busy => nr=0]) endmodule

Action Language Verifier An infinite state symbolic model checker n Uses composite symbolic representation to encode a system defined by (S, I, R) n – S: set of states, I: set if initial states, R: transition relation n Maps each variable type to a symbolic representation type – Maps boolean and enumerated types to BDD representation – Maps integer type to arithmetic constraint representation n Uses a disjunctive representation to combine symbolic representations – Each disjunct is a conjunction of formulas represented by different symbolic representations

Conjunctive Decomposition Each composite atom is a conjunction n Each conjunct corresponds to a different symbolic representation n – x: integer; y: boolean; h heap – x>0 and x’=x+1 and y´ y • Conjunct x>0 and x´ x+1 will be represented by arithmetic constraints • Conjunct y´ y will be represented by a BDD – Advantage: Image computations can be distributed over the conjunction (i. e. , over different symbolic representations).

BDDs n n n Efficient representation for boolean functions Disjunction, conjunction complexity: at most quadratic Negation complexity: constant Equivalence checking complexity: constant or linear Image computation complexity: can be exponential

Arithmetic Constraint-Based Verification n Can we use linear arithmetic constraints as a symbolic representation? – Required functionality • Disjunction, conjunction, negation, equivalence checking, existential variable elimination n Advantages: – Arithmetic constraints can represent infinite sets – Heuristics based on arithmetic constraints can be used to accelerate fixpoint computations • Widening, loop-closures

Linear Arithmetic Constraints Disjunction complexity: linear n Conjunction complexity: quadratic n Negation complexity: can be exponential n – Because of the disjunctive representation n Equivalence checking complexity: can be exponential – Uses existential variable elimination n Image computation complexity: can be exponential – Uses existential variable elimination

Linear Arithmetic Constraints Can be used to represent sets of valuations of unbounded integers n Linear integer arithmetic formulas can be stored as a set of polyhedra n where each ckl is a linear equality or inequality constraint and each is a polyhedron

A Linear Arithmetic Constraint Manipulator n Omega Library [Pugh et al. ] – Manipulates Presburger arithmetic formulas: First order theory of integers without multiplication – Equality and inequality constraints are not enough: Divisibility constraints are also needed (a variable is divisible by a constant) Existential variable elimination in Omega Library: Extension of Fourier-Motzkin variable elimination to integers n Eliminating one variable from a conjunction of constraints may double the number of constraints n Integer variables complicate the problem even further n

Fourier-Motzkin Variable Elimination n Given two constraints bz and az we have a abz b n We can eliminate z as: z. a abz b if and only if a b real shadow n Every upper and lower bound pair can generate a separate constraint, the number of constraints can double for each eliminated variable

Integers are More Complicated n If z is integer z. a abz b if a + (a - 1)(b - 1) b dark shadow n Remaining solutions can be characterized using periodicity constraints in the following form: z. + i = bz

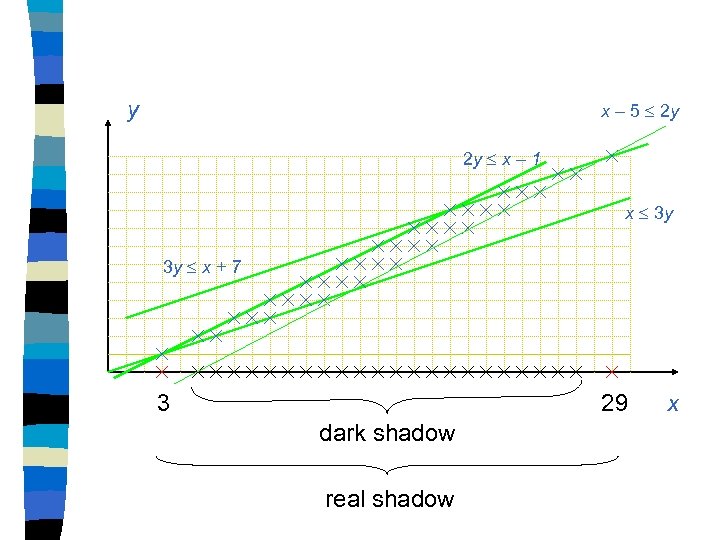
Consider the constraints: y. 0 3 y – x 7 1 x – 2 y 5 We get the following bounds for y: 2 x 6 y 3 x - 15 6 y 6 y 2 x + 14 6 y 3 x - 3 When we combine 2 lower bounds with 2 upper bounds we get four constraints: 0 14 , 3 x , x 29 , 0 12 Result is: 3 x 29

y x – 5 2 y 2 y x – 1 x 3 y 3 y x + 7 3 29 dark shadow real shadow x

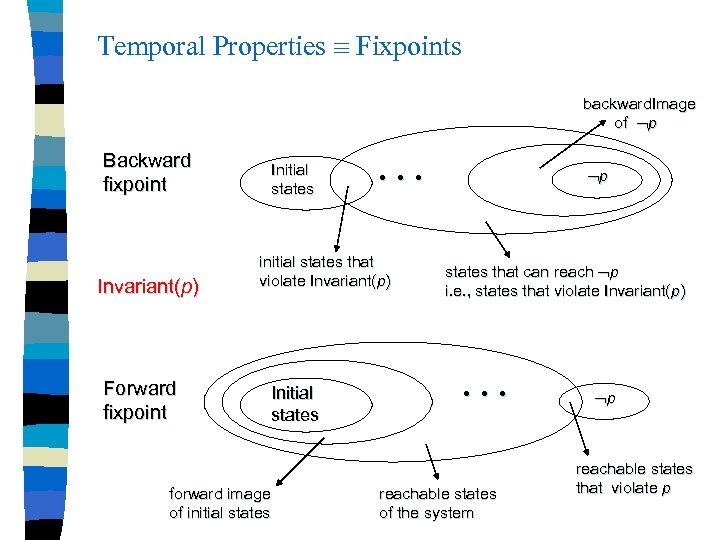Temporal Properties Fixpoints backward. Image of p Backward fixpoint Invariant(p) Initial states initial states that violate Invariant(p) Forward fixpoint forward image of initial states Initial states p • • • states that can reach p i. e. , states that violate Invariant(p) • • • reachable states of the system p reachable states that violate p

Simplification Example (y z´ = z + 1) ((y x) z´ = z + 1) (x z´ = z + 1) ((x y) z´ > z) ((x y) (z´ = z + 1 z´ > z)) ((x y) z´ z) ((x y) z´ > z)

Polymorphic Verifier Symbolic Tran. Sys: : check(Node *f) { • • • Symbolic s = check(f. left) case EX: s. backward. Image(trans. Relation) case EF: do snew = s sold = s snew. backward. Image(trans. Relation) s. union(snew) while not sold. is. Equal(s) • • • } Action Language Verifier is polymorphic When there are no integer variable it becomes a BDD based model checker