Automated Theorem Proving PVS Alexander Serebrenik 1

Automated Theorem Proving: PVS Alexander Serebrenik 1

Before We Start • PVS is installed at svstud. – no password for svstud? – contact Jan de Jong of the Notebook Service center: HG 8. 86, tel. 2979 • Install an X Windows client on your laptop – built-in for Linux – for Windows, e. g. , Exceed (via BCF) • On Wednesday we will meet in Auditorium 9 (laptop lecture hall). 2

Last Time • Foundations of Automated Theorem Proving – soundness and completeness – Gentzen’s sequent – system G for • propositional calculus • first order logics with equality 3

Today • PVS (Prototype Verification System) – Developed at SRI International – Open Source (GPL) since 1993 – Runs on Linux/Solaris/Mac – Uses Emacs as Interface – Supports System G reasoning… – and much, much more! 4

Applications of PVS • • Both academic and industrial: Verification of Javacard applets Hardware verification Protocol specification and verification Formal Mathematics Safety-critical systems. . . see http: //pvs. csl. sri. com/users. shtml 5

First Example (3 b) x. A(x) x. B(x) x(A(x) B(x)) ex 3 b: THEORY BEGIN T: TYPE x: VAR T A, B: [T -> bool] some type variable of this type predicate (function to booleans) statement: THEOREM ((FORALL x: A(x)) AND (FORALL x: B(x)) IMPLIES (FORALL x: (A(x) AND B(x)))) END ex 3 b 6

Sequent System G PVS A 1, …, An B 1, …, Bm [-1] A 1, …, [-n] An |-------{1} B 1, …, [m] Bm 7

Proof (1) |------{1} ((FORALL x: A(x)) AND (FORALL x: B(x)) IMPLIES (FORALL x: (A(x) AND B(x)))) Rule? (flatten) (skolem 1 “y 1”) [-1] (FORALL x: A(x)) [-2] B(x)) [-2] (FORALL x: B(x)) |------{1} (FORALL x: (A(x) AND B(x))) {1} (A(y 1) AND B(y 1)) Rule? (split) …yields 2 subgoals: The second statement. 1 : subgoal is [-1] (FORALL x: A(x)) [-2] (FORALL x: B(x)) postponed |------{1} A(y 1) 8 Rule? (skolem reference newname)

Proof (2) [-1] (FORALL x: A(x)) [-2] (FORALL x: B(x)) |------{1} A(y 1) Rule? (inst -1 “y 1”) Instantiating the top quantifier in -1 with the terms: y 1, This completes the proof of that The subgoal Instantiating the top quantifier statement. 1. we have in -2 with the terms: y 1, statement. 2 postponed. This (FORALL the proof of [-1] completesx: A(x)) statement. 2. x: B(x)) [-2] (FORALL |------Q. E. D. B(y 1) {1} Rule? (inst -2 “y 1”) (inst reference term) 9

PVS Proof Commands (flatten) formula to list of formulas ( : left), ( : right), ( : left), ( : right) (split) formula to a number of proof obligations (inst reference term) (skolem reference newname) replace variable by ( : right), ( : left) a term replace variable by ( : left), ( : right) a fresh variable (constant) 10

NB: Flatten and Split • PVS is smarter than just one step of System G • Flatten and split will apply the corresponding rules as long as they are applicable. |------{1}(A IMPLIES B) IMPLIES ((A IMPLIES NOT B) IMPLIES NOT A) flatten {-1} (A IMPLIES B) {-2} (A IMPLIES NOT B) {-3} A |------- 11

PVS System Tour • QQ: Watch the video. What steps did I perform? 12

PVS System Tour 1. Specify (any editor) 2. Parse (M-x parse, M-x pa) • • syntactic checks, e. g. , misspellings done by the system automatically when needed 3. Type check (M-x typecheck, M-x tc) • • semantic checks, e. g. , undeclared names builds Type Correctness Conditions • should be proved! 4. Prove (M-x prove, M-x pr) • that is what we have done before 13

QQ: First Steps with PVS • • Recall Exercise 1 b from the Instruction: (A B) ((A B) A) Write a PVS specification, corresponding to this exercise ex 1 b: THEORY BEGIN A, B: bool statement: THEOREM (A IMPLIES B) IMPLIES ((A IMPLIES NOT B) IMPLIES NOT A) END ex 1 b 14

Theory identifier PVS Language ex 3 b: THEORY BEGIN T: TYPE Type declaration Variable declaration x: VAR T A, B: [T -> bool] Constant declarations Formula declaration statement: THEOREM ((FORALL x: A(x)) AND (FORALL x: B(x)) IMPLIES (FORALL x: (A(x) AND B(x)))) END ex 3 b 15

“Theory Header” • Theory identifier ex 3 b: THEORY • List of formal parameters stacks [t: TYPE+] : THEORY groups [G : TYPE, e : G, o : [G, G->G], inv : [G->G] ] : THEORY 16

Types (1) • Uninterpreted types: – might be empty T: TYPE – non-empty T: TYPE+ • Interpreted types: T: TYPE = type expression • Subtypes: S: TYPE FROM T 17

Types (2) • Type expressions – builtins bool, int – enumerated {r, g, b} – functions [int, bool -> int] – tuples [int, int] – predicate-based (p) • shorthand for {x | p(x)} 18

Types: QQ • Functional is a function that takes functions as its argument and returns a real number. • Define the type of functionals for functions from T 1 to T 2 T 1, T 2: TYPE FT: TYPE = [[T 1 -> T 2] -> real] 19

Variable Declarations • either with VAR – x: VAR bool • or within a binding expression ( , , λ) – FORALL (x: int): (EXISTS (x: nat) p(x)) AND q(x)) 20

Constant Declarations • Constants: n: int, c: int = 3 – The underlying type should be non-empty • Functions are also constants: – f: [int -> int] = (lambda (x: int): x+1) – f(x: int): int = x + 1 • QQ: What does f(x: (p)): int = x+1 mean for a predicate p? – (p)shorthand for {x | p(x)} 21

Boolean Functions • a. k. a. predicates • Can be written as subsets: – odd: [nat -> bool] = {n: nat | EXISTS (m: nat): n = 2 * m + 1} instead of – odd: [nat -> bool] = (LAMBDA (n: nat): EXISTS (m: nat): n = 2 * m + 1) 22

Recursive Functions • No mutual recursion • Function should be total • Termination should be ensured: MEASURE fac(x: nat): RECURSIVE nat = IF x=0 THEN 1 ELSE x*fac(x-1) ENDIF MEASURE x 23

MEASURE • Can be followed by any function: – MEASURE lambda (n: nat): n – MEASURE N-I • QQ: Find an appropriate MEASURE for p(x: int): RECURSIVE int = (IF (x > 1 AND x < 1000) THEN p(x*x) ELSIF (x < -1 AND x > -1000) THEN p(-x*x) ELSE 0 ENDIF) 24

MEASURE: Solution p(x: int): RECURSIVE int = (IF (x > 1 AND x < 1000) THEN p(x*x) ELSIF (x < -1 AND x > -1000) THEN p(-x*x) ELSE 0 ENDIF) MEASURE pmeas(x: int): nat = (IF (x > 1 AND x < 1000) THEN 1000 -x ELSIF (x < -1 AND x > -1000) THEN 1000+x ELSE 0 ENDIF) 25

Formula Declarations • AXIOM is a formula that can be recalled at any moment of the proof. – use (lemma name <substitution>) • THEOREM (or LEMMA) is a formula one likes to prove. • May contain free variables: p(x) is equivalent to (FORALL x: p(x)) 26

AXIOMs in Practice pop_push: AXIOM pop(push(x, s)) = s pop 2 push 2: THEOREM pop(push(x, push(y, s)))) = s |------{1} pop(push(X, push(Y, S)))) = S Rule? (lemma pop_push) Applying pop_push this simplifies to: {-1} FORALL (s: stack, x: t): pop(push(x, s)) = s |------[1] pop(push(X, push(Y, S)))) = S 27

Functions Can Be Defined Using AXIOMs 1. f: [int -> int] = (lambda (x: int): x+1) 2. f: [int -> int] f: AXIOM f = (LAMBDA (x: int): x+1) NB! New declaration preserves consistency of theory, new axiom might not! 28

Between AXIOM and THEOREM groups [G : TYPE, e : G, o : [G, G->G], inv : [G->G] ] : THEORY BEGIN ASSUMING a, b, c : VAR G associativity : ASSUMPTION a o (b o c) = (a o b) o c unit : ASSUMPTION e o a = a AND a o e = a inverse : ASSUMPTION inv(a) o a = e AND a o inv(a) = e ENDASSUMING 29

ASSUMPTIONs • Appear only between ASSUMING and ENDASSUMING • Usually formulated in terms of parameters of theory • When theory is used, e. g. IMPORTING[int, 0, +, -] assumptions become proof obligations (TCCs). 30

Theory Is Used? • EXPORTING specifies names that should be visible to the IMPORTING theories – by default, all names are visible • IMPORTING makes visible names of another theory available for the current one. – IMPORTINGs are cumulative – Beware the name clashes 31

Summary So Far (1) • Lifecycle of a PVS specification: specify, parse, type check, prove. • Specification consists of the “header” followed by type, variable, constant and formula declarations. • Types: uninterpreted, interpreted. – Type expressions: builtins, enumerated, functions, tuples, predicate-based 32

Summary So Far (2) • Recursive functions should be provided by MEASURE. • Formula declarations: AXIOMs, ASSUMPTIONs and THEOREMs. – AXIOMs can be recalled using the lemma proof command. • Adding a new AXIOM does not guarantee consistency of theory. • Theories can EXPORT and IMPORT names. 33

Type Check • Executed upon M-x typecheck, or M-x tc. • Generate additional proof obligations (theorems) ensuring – type correctness; – termination; – non-emptiness of a type, if constants of this type are being declared. 34

Closer Look at Factorial % Subtype TCC for 1 Termination TCC x - fac(x - 1) • exfac typechecked in. FORALL (x: TCCs, fac_TCC 2: OBLIGATION fac_TCC 1: OBLIGATION 0. 27 s: 2 0 FORALL x 0 subsumed, 2 unproved, nat): NOT (x: = nat): NOT xx =- 01 >= 0; 0 IMPLIES – TCC = The x - 1 < x; type correctness condition IMPLIES argument of the • recursive call should be a M-x show-tccs number as well. natural fac(x: nat): RECURSIVE nat = IF x=0 THEN 1 ELSE x*fac(x-1) ENDIF MEASURE x 35

TCCs and Proofs • TCCs can be postponed but ultimately should be proved. • Failure to prove TCC might indicate that the statement is not valid! • Automated attempt to prove the TCCs: x typecheck-prove (M-x tcp) M- 36

Summary: Prove Commands control structure system G decision procedures definitions and lemmas miscellaneous fail, postpone, undo, … copy, hide-all-but, reveal, … split, flatten, inst, skolem, … assert, grind, … lemma, expand, … case, induct, replace, … 37

What If? • PVS crashes in the middle of a proof: (restore) • you do not know what to do: (help) or (help command) • you want to stop the proof attempt: (quit) • you want to go to next remaining goal: (postpone) • you want to revise your last step: (undo) 38

Manipulating Sequents • If some information is needed twice during the proof: (copy) • If some information is no longer needed: (delete) • If some information might be needed later but is cluttering now: (hide) • If some hidden information is needed: M-x show-hidden followed by (reveal reference) 39

Example sum: THEORY BEGIN n: VAR nat sum(n): RECURSIVE nat = (IF n=0 THEN 0 ELSE n+sum(n-1) ENDIF) MEASURE (LAMBDA n: n) closed_form: THEOREM sum(n) = (n * (n+1))/2 END sum 40

$closed_form : |------{1} FORALL (n: nat): sum(n) = (n * (n + 1)) /$

closed_form : |------{1} FORALL (n: nat): sum(n) = (n * (n + 1)) / 2 Rule? (induct "n") Inducting on n on formula 1, this yields closed_form. 1 : |------QQ: {1} sum(0) = (0 * (0 + 1)) / 2 2 subgoals: What are the two subgoals? Induction base Rule? (expand “sum") Expanding the definition of sum, this simplifies to: closed_form. 1 : |------{1} 0 = 0 / 2 Rule? (assert) Simplifying, rewriting, and recording with decision procedures. This completes the proof of closed_form. 1. 41

$closed_form. 2 : Induction step |------{1} FORALL j: sum(j) = (j * (j +$

closed_form. 2 : Induction step |------{1} FORALL j: sum(j) = (j * (j + 1)) / 2 IMPLIES sum(j + 1) = ((j + 1) * (j + 1)) / 2 Rule? (skosimp) Skolemizing skolem using standard names +to: skosimp = and flattening, this simplifies flatten closed_form. 2 : {-1} sum(j!1) = (j!1 * (j!1 + 1)) / 2 |------{1} sum(j!1 + 1) = ((j!1 + 1) * (j!1 + 1)) / 2 We would like to use expand but only in the succedent! Rule? (expand “sum” +) Expanding the definition of sum, this simplifies to: closed_form. 2 : [-1] sum(j!1) = (j!1 * (j!1 + 1)) / 2 |------{1} 1 + sum(j!1) + j!1 = (2 + j!1 + (j!1 * j!1 + 2 * j!1)) / 2 42

Expanding the definition of sum, this simplifies to: Induction step closed_form. 2 : [-1] sum(j!1) = (j!1 * (j!1 + 1)) / 2 |------{1} 1 + sum(j!1) + j!1 = (2 + j!1 + (j!1 * j!1 + 2 * j!1)) / 2 Rule? (assert) Simplifying, rewriting, and recording with decision procedures, This completes the proof of closed_form. 2. Q. E. D. 43

Proof Commands In the Example • (induct n) – induction on variable n • (expand “name” ref) – expand definition name in ref: – number – “-” all antecedents – “+” all succedents • (skosimp) – skolem with standard names and (flatten) • (assert) – prove or simplify using the builtin decision procedures 44

Replace {-1} X = Y |------{1} Y = X Replace the left-hand side of (-1) in (1) by the right-hand side of (-1). Rule? (replace -1 1) If you add rl: Replacing using formula -1, this simplifies to: (replace -1 1 rl) [-1] X = Y |------{1} TRUE the rewriting will go from right to left. 45

stacks [t: TYPE+] : THEORY BEGIN stack : TYPE+ s : VAR stack empty : stack nonemptystack? (s) : bool = s /= empty push : [t, stack -> (nonemptystack? )] pop : [(nonemptystack? ) -> stack] x, y : VAR t pop_push : AXIOM pop(push(x, s)) = s pop 2 push 2: THEOREM pop(push(x, push(y, s)))) = s END stacks QQ: To prove pop 2 push 2 you might like to use A. expand B. induct C. replace 46

More Proof Commands • case - distinguish between different cases. • propax – proves propositional axioms, i. e. , – false as an antecedent, – true or t=t as a succedent – common formula for antecedent and succedent • grind – “black magic” but often works: – – rewrite using lemmas simplify numerical expressions performs equality substitutions makes use, e. g. , of assert and replace • smash – propositional and ground simplification 47

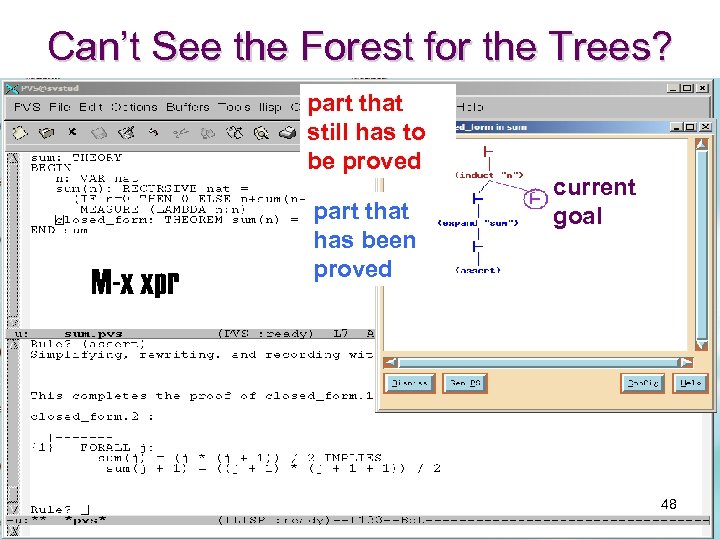
Can’t See the Forest for the Trees? part that still has to be proved M-x xpr part that has been proved current goal 48

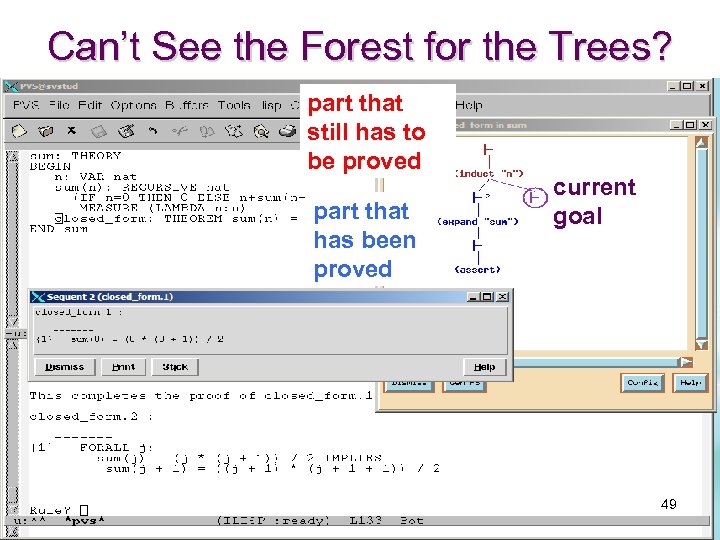
Can’t See the Forest for the Trees? part that still has to be proved part that has been proved current goal 49

And Even More • You can also create La. Te. X documentation: M-x latex-theory-view (M-x ltv) • PS proofs can be generated from the graphic user interface. • … or first in La. Te. X: M-x latex-proof 50

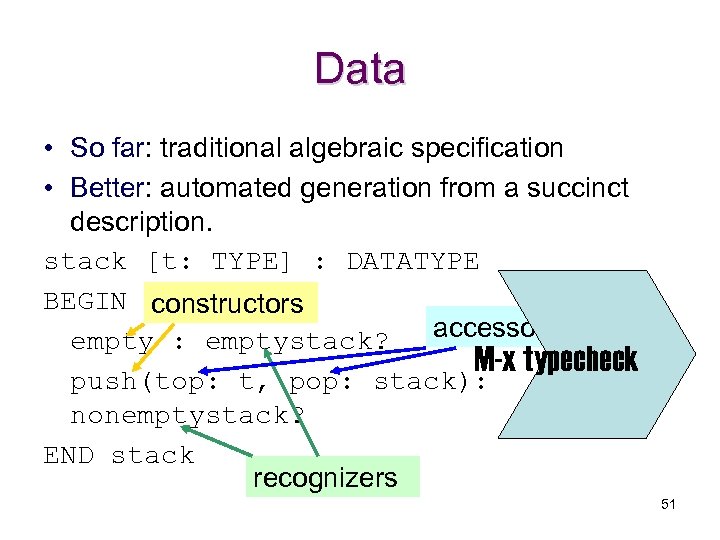
Data • So far: traditional algebraic specification • Better: automated generation from a succinct description. stack [t: TYPE] : DATATYPE BEGIN constructors accessors empty : emptystack? M-x typecheck push(top: t, pop: stack): nonemptystack? END stack recognizers 51

What Is Generated From a Datatype? • extensionality axioms for the constructors • accessor/constructor axioms – stack_pop_push: AXIOM (FORALL (v 1: t, v 2: stack) pop(push(v 1, v 2)) = v 2) • induction scheme • recursive combinator • look at stack_adt. pvs 52

Example: Recursive Combinator reduce_nat(emptystack? _fun: nat, nonemptystack? _fun: [[t, nat] -> nat]): [stack -> nat] = LAMBDA (stack_var: stack): CASES stack_var OF empty: emptystack? _fun, push(push 1_var, push 2_var): nonemptystack? _fun(push 1_var, reduce_nat(emptystack? _fun, nonemptystack? _fun)(push 2_var)) ENDCASES QQ: What does the following call calculate: reduce_nat(0, (LAMBDA (x: t, n: nat): n+1))? 53

Cases? • Pattern matching: CASES stack_var OF empty: …, push(push 1_var, push 2_var): …)) ENDCASES • Can contain ELSE covers all constructors not covered before. 54

Putting It All Together stack: DATATYPE BEGIN empty : emptystack? push(top: t, pop: stack): nonemptystack? END stack length: THEORY BEGIN t: TYPE IMPORTING stack_adt[t] length(s: stack): nat = reduce_nat(0, (LAMBDA(x: t, n: nat): n+1))(s) l 0: THEOREM (length(empty) = 0) END length 55

Many Data Types and Theories • can be consulted by M-x vpt – view prelude theory • are “built in” and described in the Prelude, include – logics, functions, numbers – relations, sets, sequences and lists – sum and quotient types – induction – μ-calculus and CTL 56

Summary: PVS • PVS System: Linux/Unix, Emacs + GUI • PVS Language: How to write a specification? – THEORY, TYPE, VAR, THEOREM, … – abstract data types • PVS Proof Checker: How do we prove? – flatten, split, inst, skolem, expand, lemma… • PVS Prelude: Built-in theories – there are even more theories in NASA libraries 57

Don’t Forget: Tomorrow • No password for svstud? – contact Jan de Jong of the Notebook Service center: HG 8. 86, tel. 2979 • Install an X Windows client on your laptop – built-in for Linux – for Windows, e. g. , Exceed (via BCF website) • We meet at 845 in Auditorium 9. 58