Automated Soundness Proofs for Dataflow Analyses and Transformations

Automated Soundness Proofs for Dataflow Analyses and Transformations via Local Rules Sorin Lerner* [graduating this year!] Todd Millstein** Erika Rice* Craig Chambers* * University of Washington ** UCLA

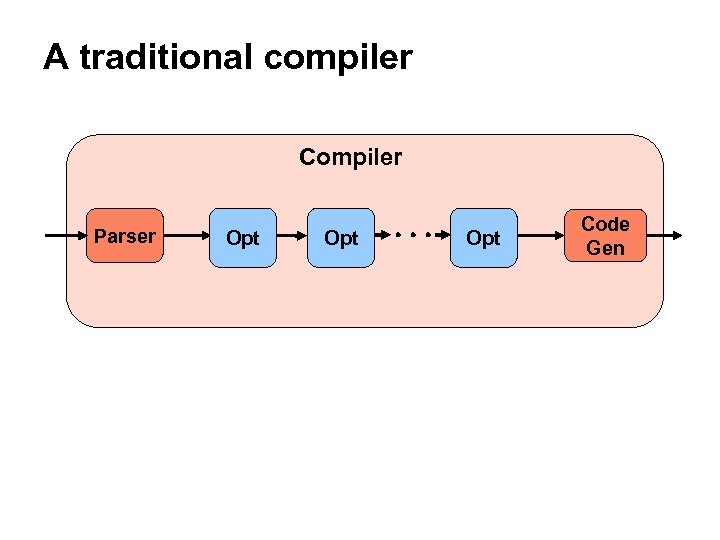A traditional compiler Compiler Parser Opt Opt Code Gen

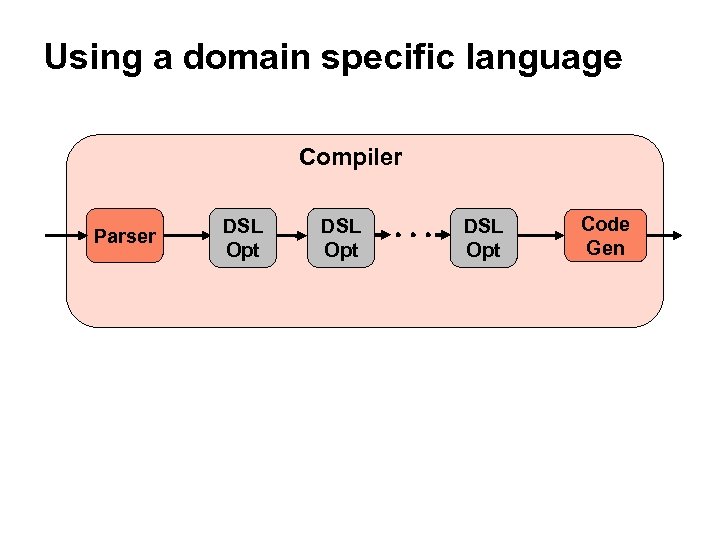Using a domain specific language Compiler Parser DSL Opt Code Gen

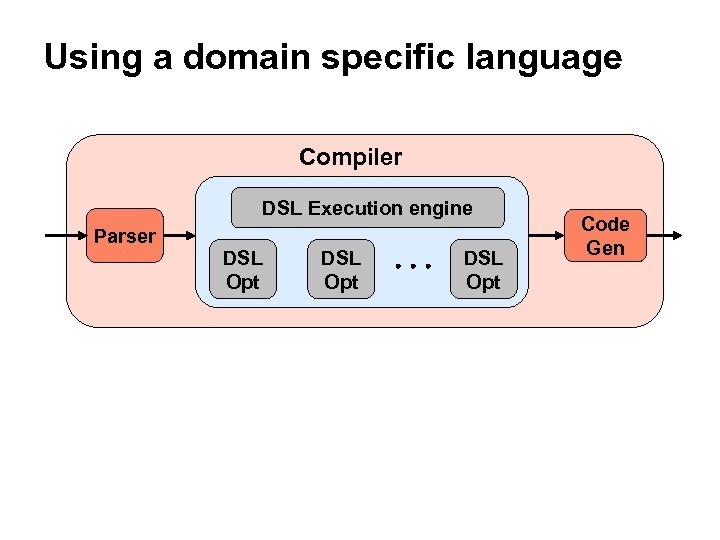Using a domain specific language Compiler DSL Execution engine Parser DSL Opt Code Gen

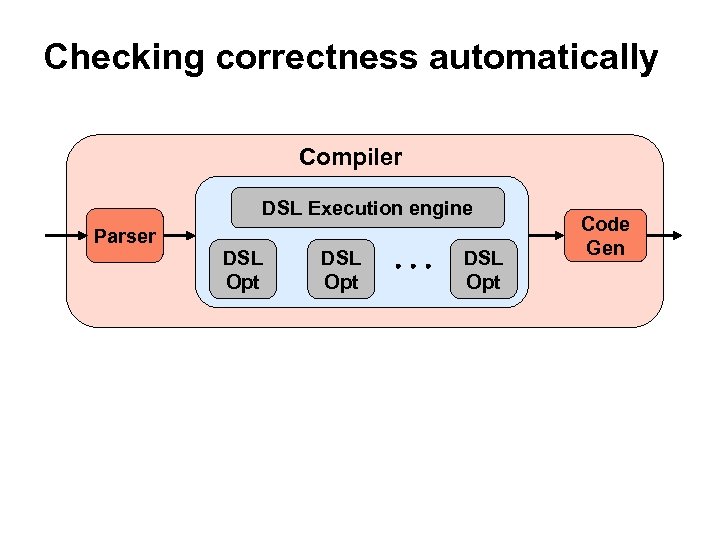Checking correctness automatically Compiler DSL Execution engine Parser DSL Opt Code Gen

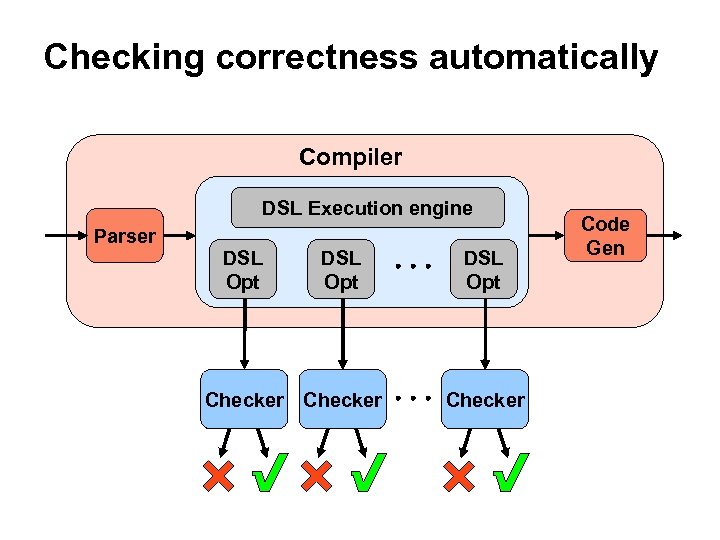Checking correctness automatically Compiler DSL Execution engine Parser DSL Opt Checker Code Gen

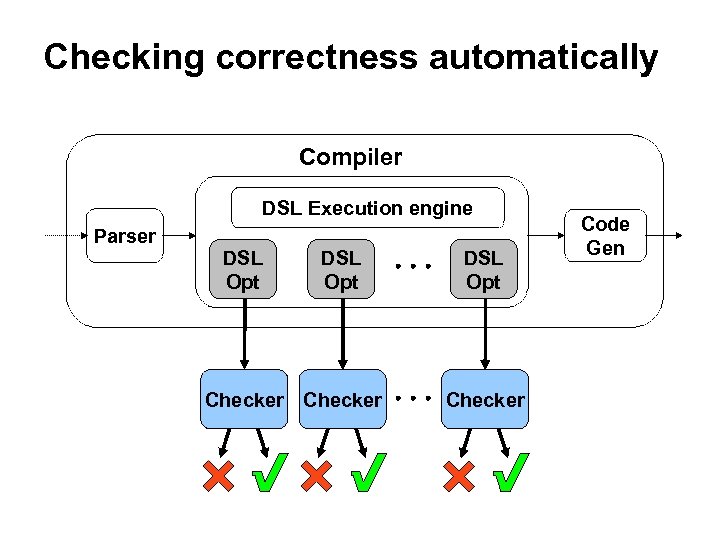Checking correctness automatically Compiler DSL Execution engine Parser DSL Opt Checker Code Gen

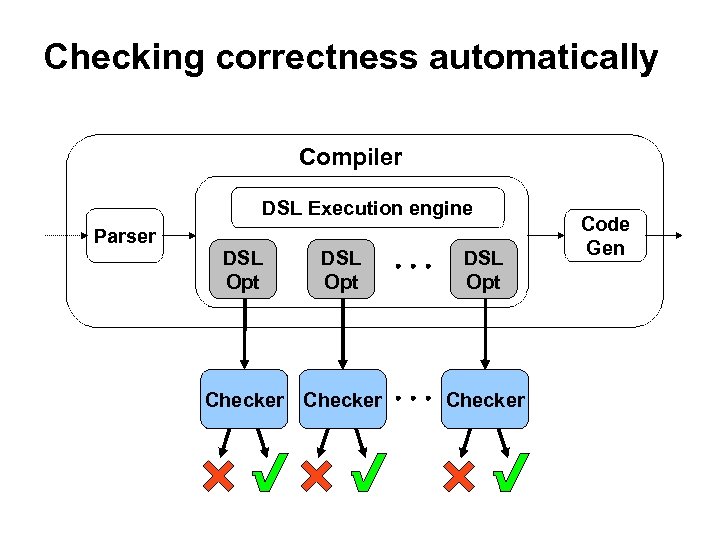Checking correctness automatically Compiler DSL Execution engine Parser DSL Opt Checker Code Gen

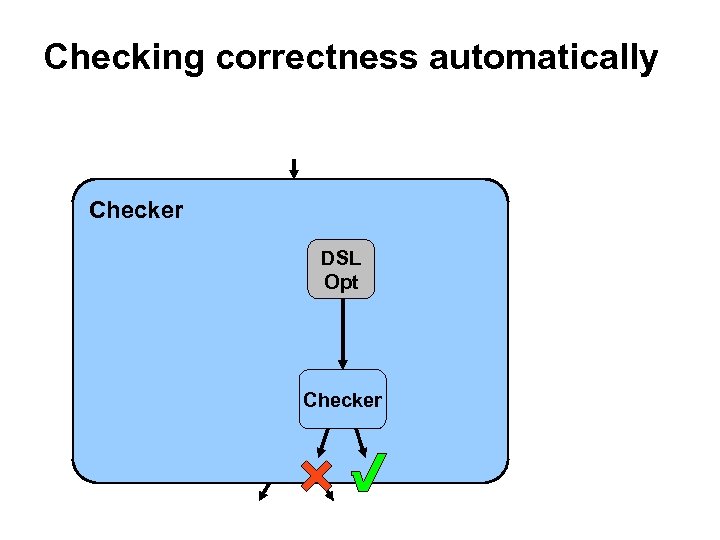Checking correctness automatically Checker DSL Opt Checker

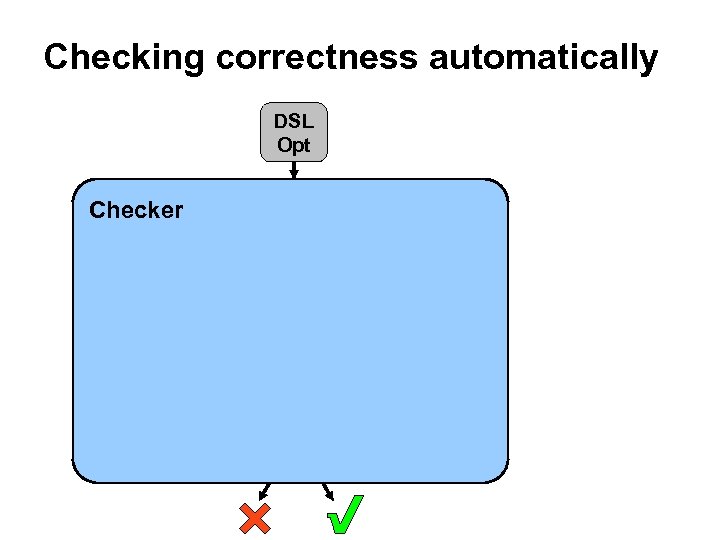Checking correctness automatically DSL Opt Checker VCGen Verification Condition (VC) Automatic Theorem Prover

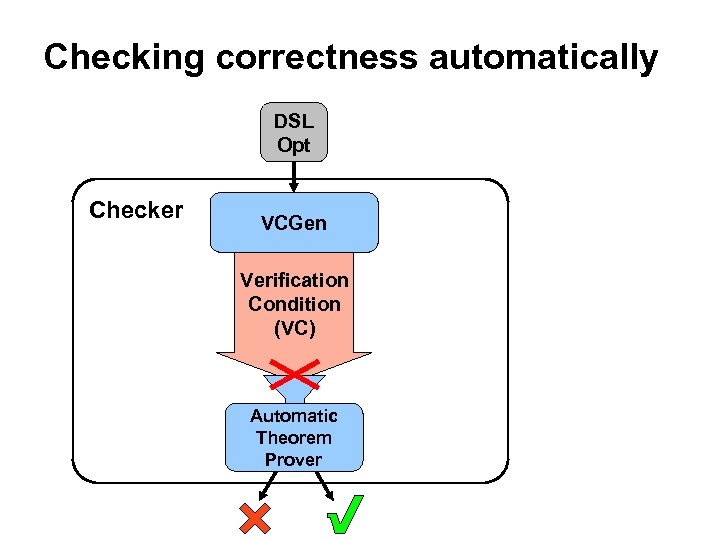Checking correctness automatically DSL Opt Checker VCGen Verification Condition (VC) Automatic Theorem Prover

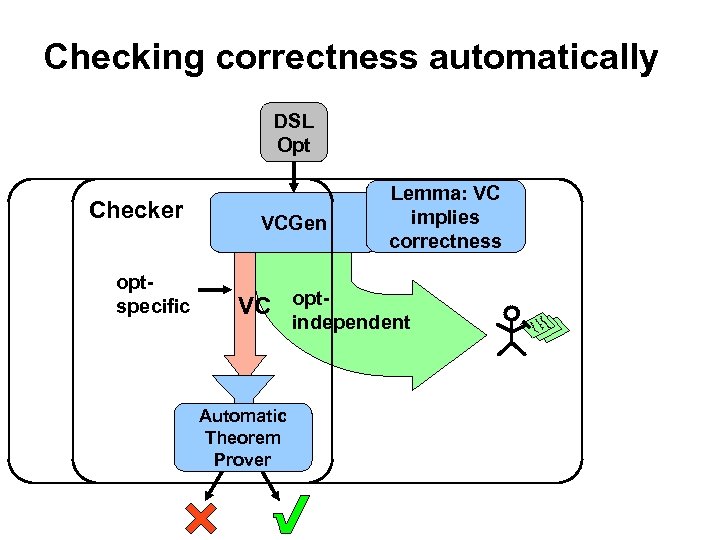Checking correctness automatically DSL Opt Checker optspecific VCGen VC opt- Lemma: VC implies correctness independent Automatic Theorem Prover

Cobalt [PLDI 03] • The Cobalt DSL is an instantiation of this architecture – An opt written in Cobalt is a rewrite rule triggered by a declarative global condition over the CFG • Expressed and automatically proved the correctness of a variety of intraprocedural optimizations, including: – const prop and folding, branch folding, CSE, PRE, DAE, partial DAE

In this talk: the Rhodium DSL • Increased expressiveness – New model for expressing opts: local propagation rules with explicit dataflow facts – Heap summaries – Infinite analysis domains – Flow-sensitive and -insensitive – Intraprocedural and interprocedural • Some Rhodium opts not expressible in Cobalt: – Arithmetic invariant detection, integer range analysis, loop-induction-variable strength reduction, Andersen's may-point-to analysis with allocation-site summaries

Outline • Overview • Rhodium by example • Checking correctness automatically • Future work, related work and conclusion

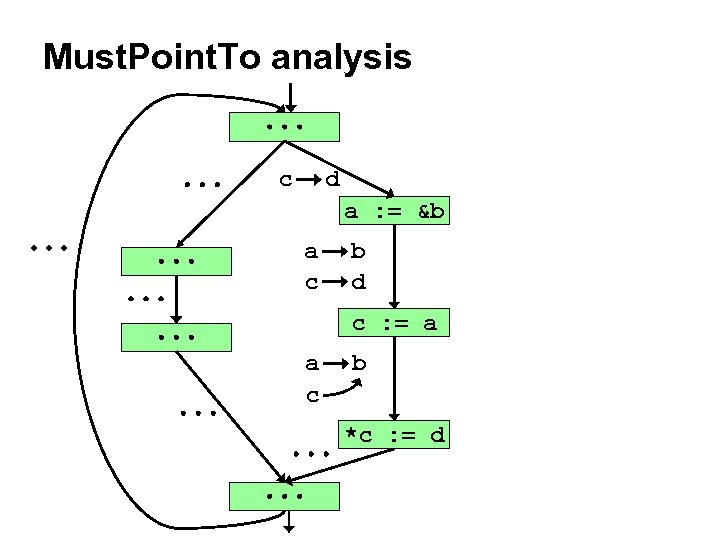Must. Point. To analysis c d a : = &b a c b d c : = a a c b *c : = d

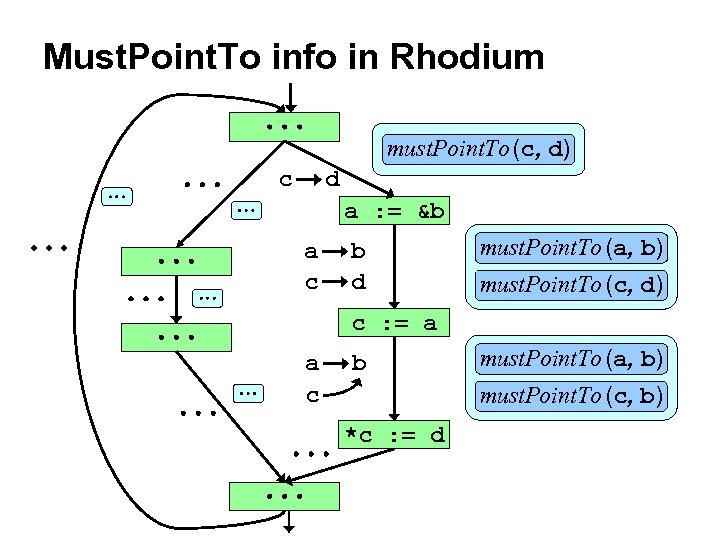Must. Point. To info in Rhodium must. Point. To (c, d) c d a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d

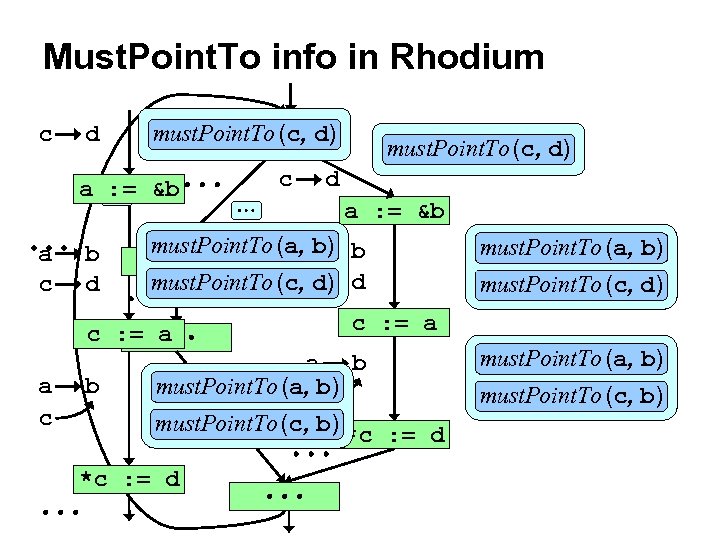Must. Point. To info in Rhodium c d must. Point. To (c, d) a : = &b a c b d a : = &b must. Point. To (a, a b b) must. Point. To (c, c d d) c : = a a c c must. Point. To (c, d) c : = a a b must. Point. To (a, cb) must. Point. To (c, b) *c : = d must. Point. To (a, b) must. Point. To (c, b)

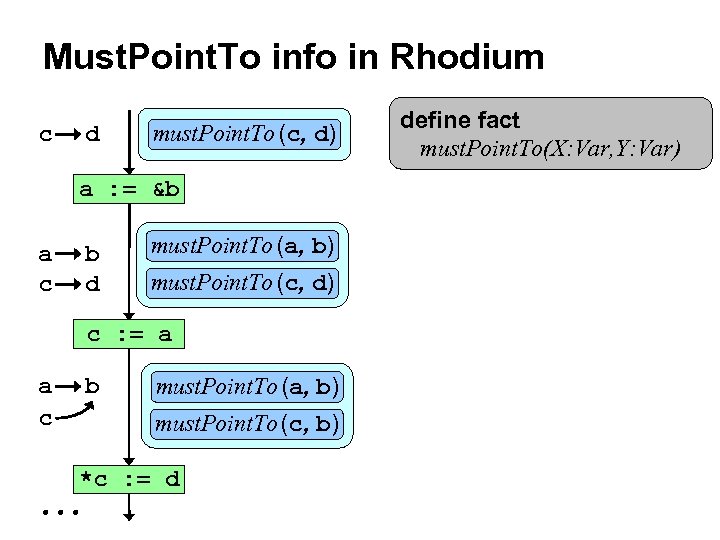Must. Point. To info in Rhodium c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var)

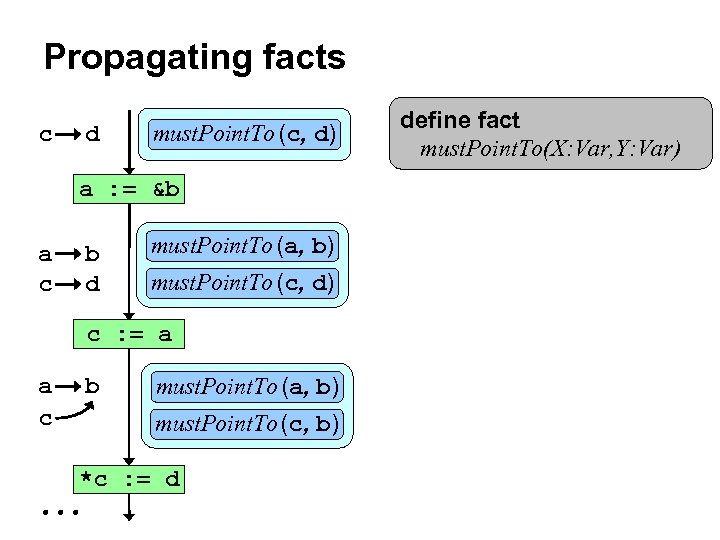Propagating facts c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var)

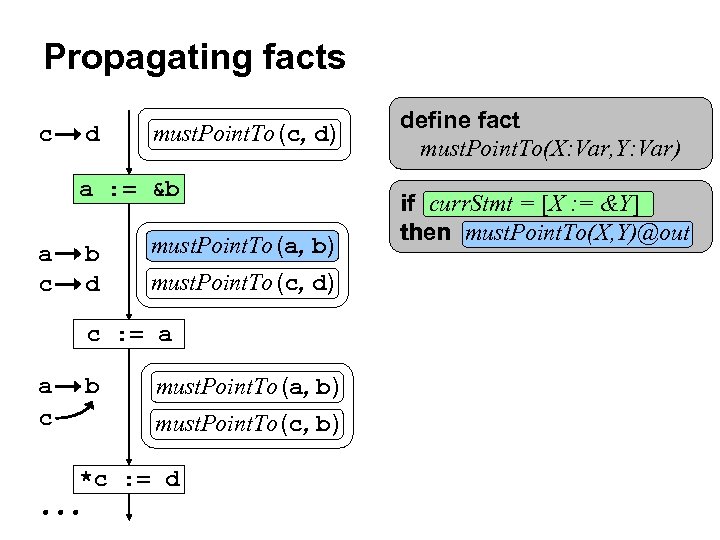Propagating facts c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var) if curr. Stmt = [X : = &Y] then must. Point. To(X, Y)@out

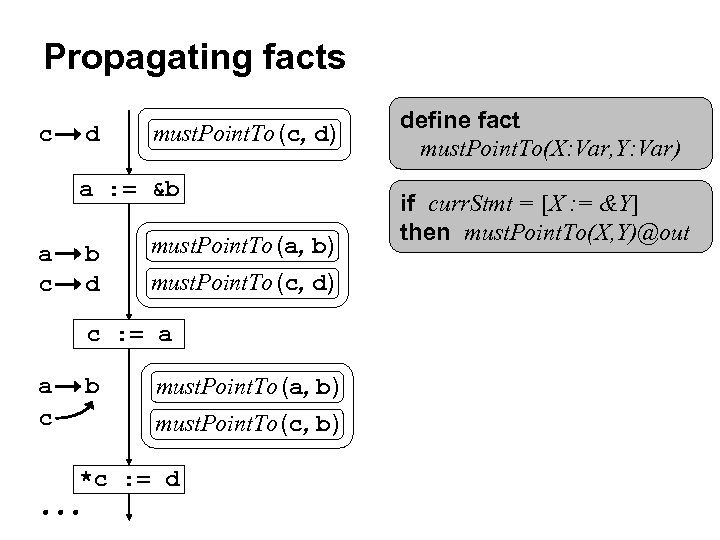Propagating facts c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var) if curr. Stmt = [X : = &Y] then must. Point. To(X, Y)@out

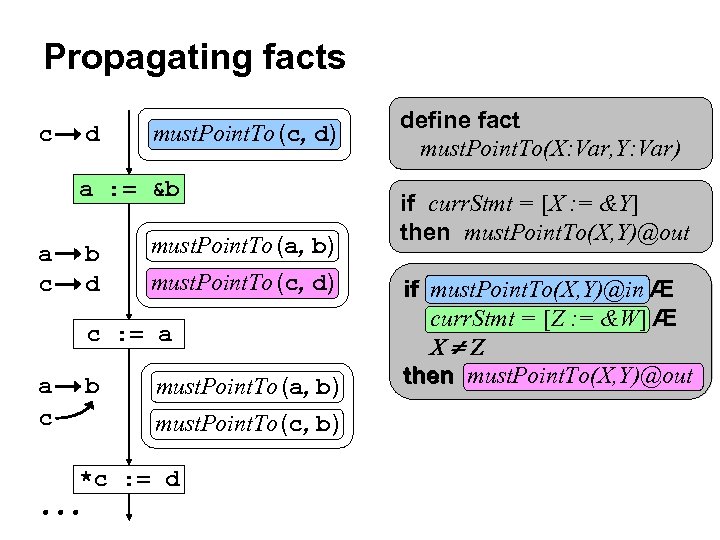Propagating facts c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var) if curr. Stmt = [X : = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = &W] Æ X Z then must. Point. To(X, Y)@out

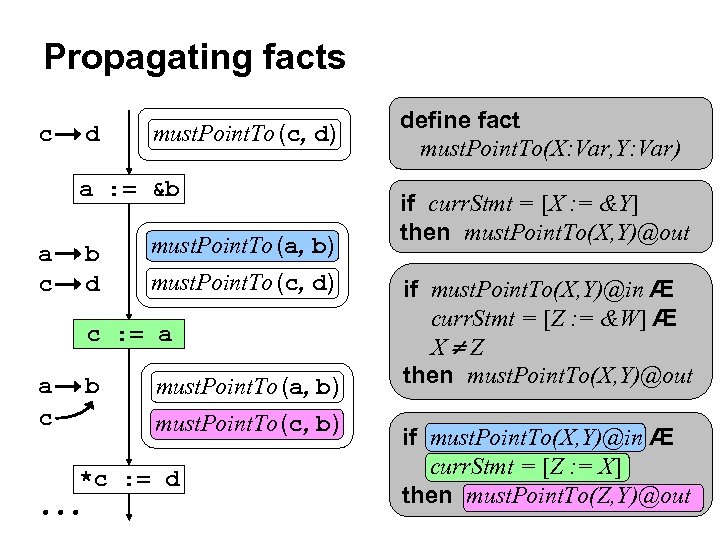Propagating facts c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var) if curr. Stmt = [X : = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = &W] Æ X Z then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = X] then must. Point. To(Z, Y)@out

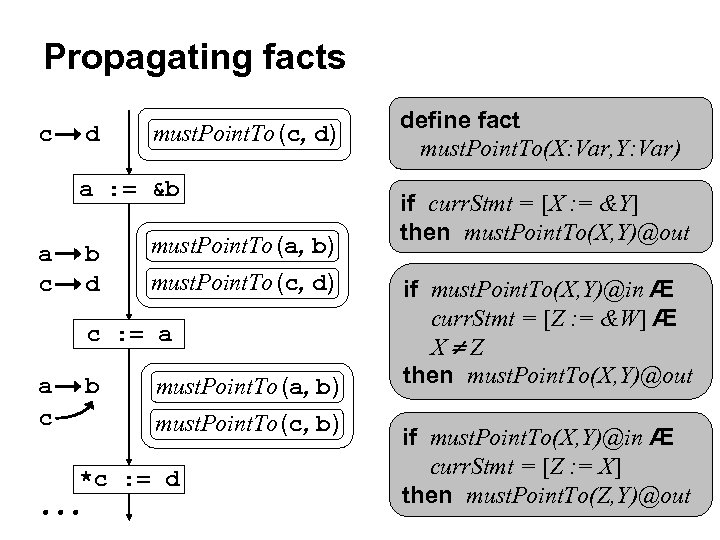Propagating facts c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var) if curr. Stmt = [X : = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = &W] Æ X Z then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = X] then must. Point. To(Z, Y)@out

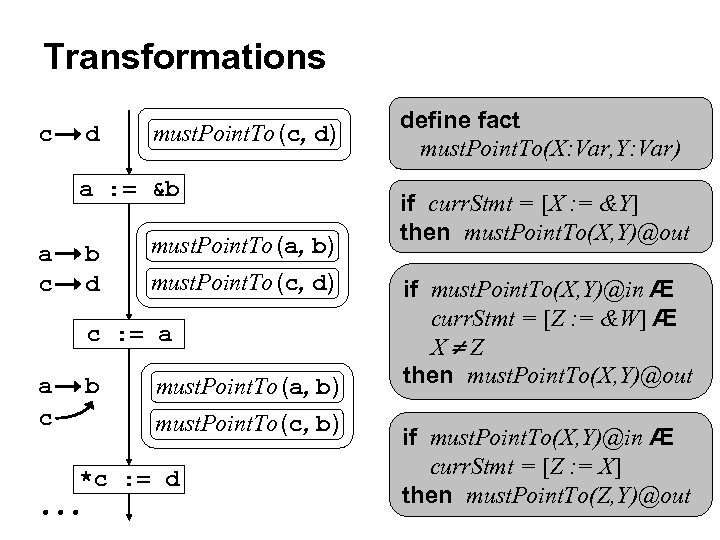Transformations c d must. Point. To (c, d) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d define fact must. Point. To(X: Var, Y: Var) if curr. Stmt = [X : = &Y] then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = &W] Æ X Z then must. Point. To(X, Y)@out if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = X] then must. Point. To(Z, Y)@out

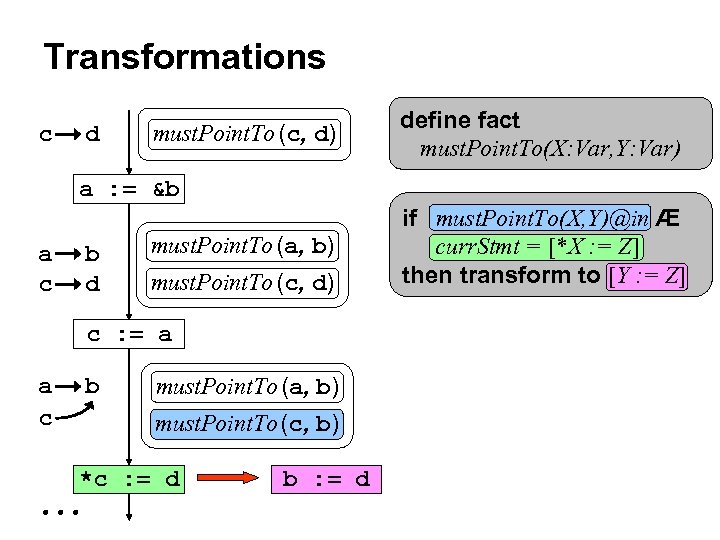Transformations c d must. Point. To (c, d) define fact must. Point. To(X: Var, Y: Var) a : = &b a c b d must. Point. To (a, b) must. Point. To (c, d) c : = a a c b must. Point. To (a, b) must. Point. To (c, b) *c : = d b : = d if must. Point. To(X, Y)@in Æ curr. Stmt = [*X : = Z] then transform to [Y : = Z]

Semantics of a Rhodium opt • Run all the propagations rules using optimistic iterative analysis starting with complete set of facts until the best fixed point is reached • Then run all transformation rules • For better precision, combine analyses and transformations using our previous composition framework [POPL 02]

More in Rhodium (see paper for details) • Mixing facts • Heap summaries • May. Point. To analysis via Must. Not. Point. To • Infinite domains • Flow-sensitive and -insensitive • Intraprocedural and interprocedural

Outline • Overview • Rhodium by example • Checking correctness automatically • Future work, related work and conclusion

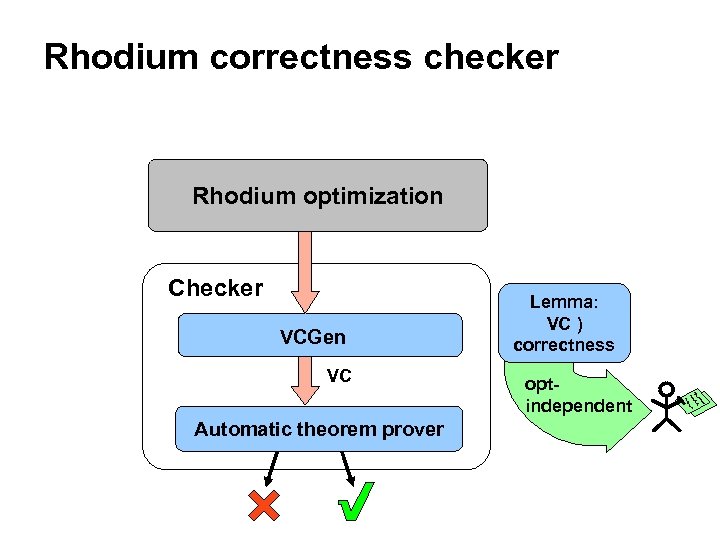Rhodium correctness checker Rhodium optimization Checker VCGen VC Automatic theorem prover Lemma: VC ) correctness optindependent

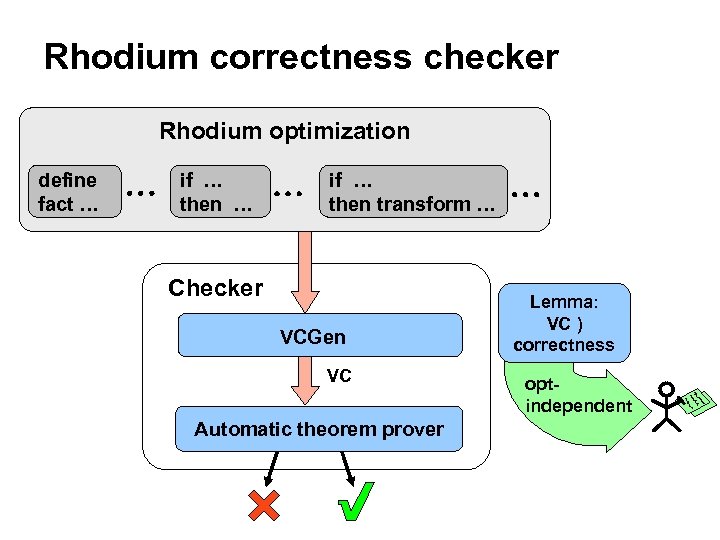Rhodium correctness checker Rhodium optimization define fact … if … then transform … Checker VCGen VC Automatic theorem prover Lemma: VC ) correctness optindependent

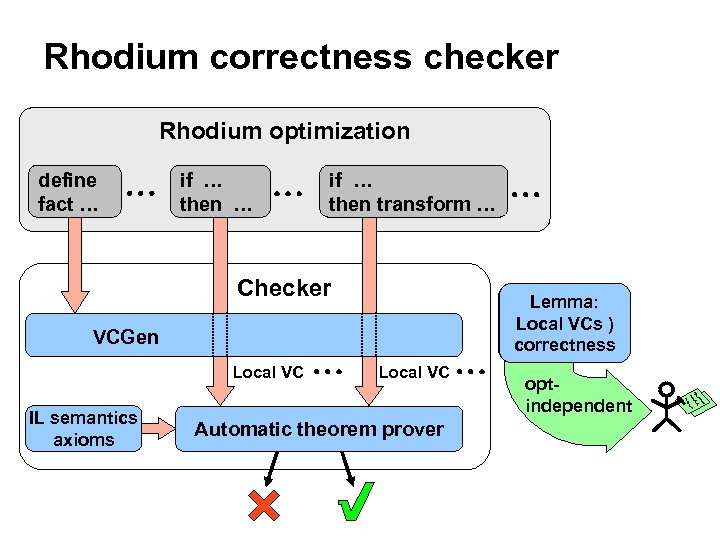Rhodium correctness checker Rhodium optimization define fact … if … then transform … Checker Lemma: Local VCs ) VC ) correctness VCGen Local VC IL semantics axioms Local VC Automatic theorem prover optindependent

Local correctness of prop. rules define fact must. Point. To(X: Var, Y: Var) if must. Point. To(X, Y)@in Æ curr. Stmt = [Z : = X] then must. Point. To(Z, Y)@out must. Point. To (X, Y) Z : = X must. Point. To (Z, Y)

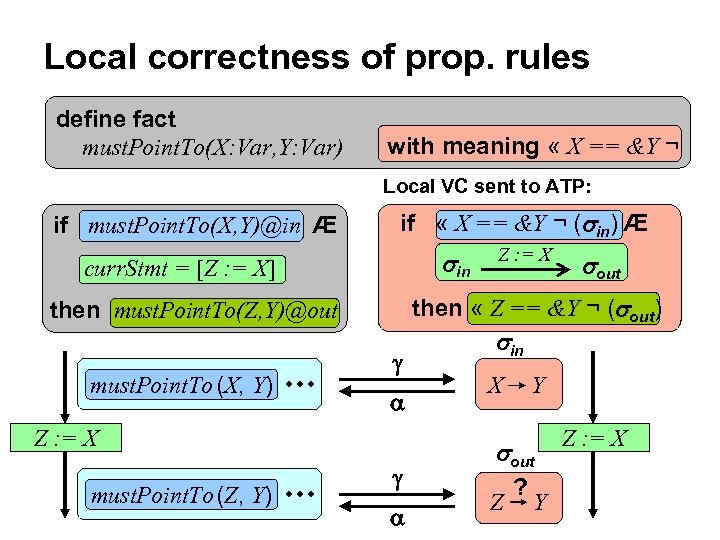Local correctness of prop. rules define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ Local VC sent to ATP: if must. Point. To(X, Y)@in Æ if « X == &Y ¬ ( in) Æ in curr. Stmt = [Z : = X] Z : = X must. Point. To (Z, Y) out then « Z == &Y ¬ ( out) then must. Point. To(Z, Y)@out must. Point. To (X, Y) Z : = X in X Y out Z ? Y Z : = X

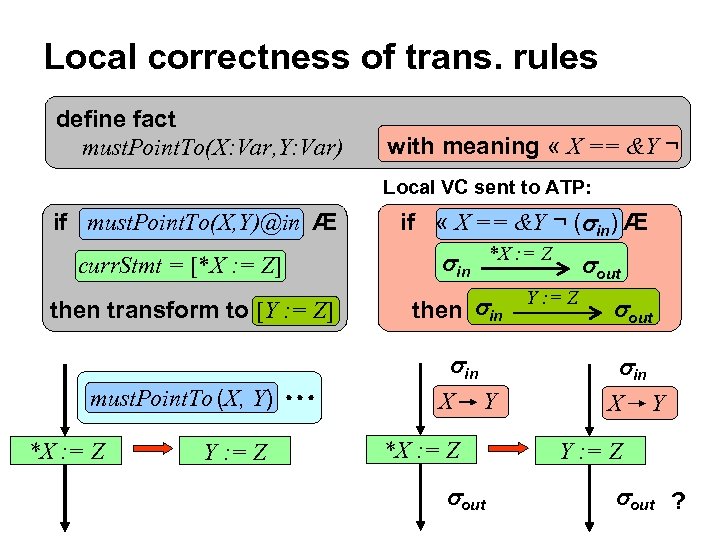Local correctness of trans. rules define fact must. Point. To(X: Var, Y: Var) with meaning « X == &Y ¬ Local VC sent to ATP: if must. Point. To(X, Y)@in Æ curr. Stmt = [*X : = Z] then transform to [Y : = Z] if « X == &Y ¬ ( in) Æ *X : = Z in Y : = Z then in must. Point. To (X, Y) *X : = Z Y : = Z out X out in Y *X : = Z out X Y Y : = Z out ?

More on correctness (see paper for details) • Heap summaries • Separating profitability from correctness • Theorem stating soundness of the framework for creating interprocedural and flow-insensitive analyses

Outline • Overview • Rhodium by example • Checking correctness automatically • Future work, related work and conclusion

Current and future work • Backward optimizations • Infer rules from just the dataflow fact declarations and their meanings • Debugging • Efficient execution engine

Some related work • Proving correctness by hand – Abstract interpretation [Cousot and Cousot 77, 79] – Partial equivalence relations [Benton 04] – Temporal logic [Lacey et al. 02] • Proving correctness with interactive theorem prover – Using Coq proof assistant [Cachera et al. 04] • Testing correctness one compilation at a time – Translation validation [Pnueli et al. 98, Necula 00] – Credible compilation [Rinard 99] • Execution engines – Incremental execution of transformations [Sittampalam et al. 04] – Running opts specified with temporal logic [Steffen 91]

Conclusion • Local rules in Rhodium are more expressive than Cobalt’s global condition • The correctness checker found subtle bugs in our Rhodium opts • Good step towards pushing more of the burden of writing compilers on to the computer