Automated Planning Source Ch 1 Appendix

Automated Planning Source: • Ch. 1 • Appendix B. 3 • Dana Nau’s slides • My own Dr. Héctor Muñoz-Avila

What is Planning? Classical Definition Planning: finding a sequence of actions to achieve a goal Domain Independent: symbolic descriptions of the problems and the domain. The plan generation algorithm remains the same Advantage: - opportunity to have clear semantics Disadvantage: - symbolic description requirement Domain Specific: The plan generation algorithm depends on the particular domain Advantage: - can be very efficient Disadvantage: - lack of clear semantics - knowledge-engineering for adaptation

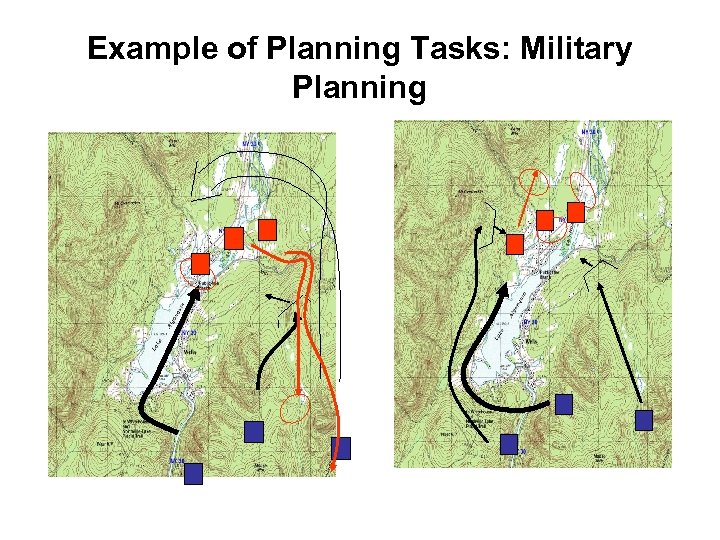Example of Planning Tasks: Military Planning

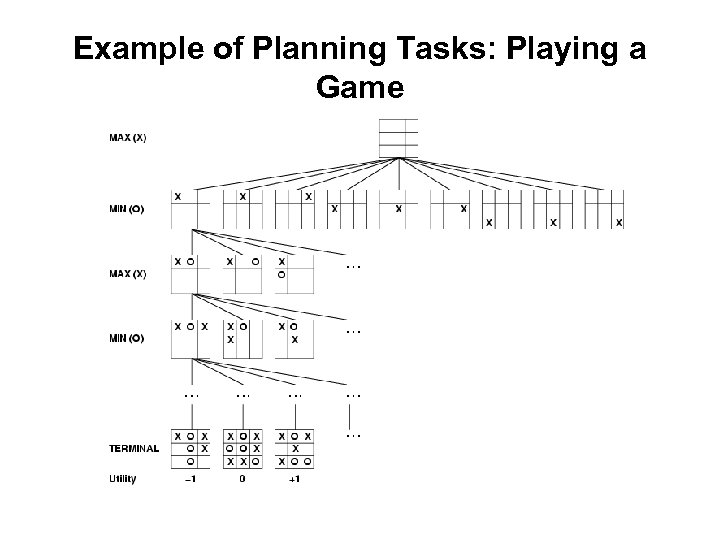Example of Planning Tasks: Playing a Game

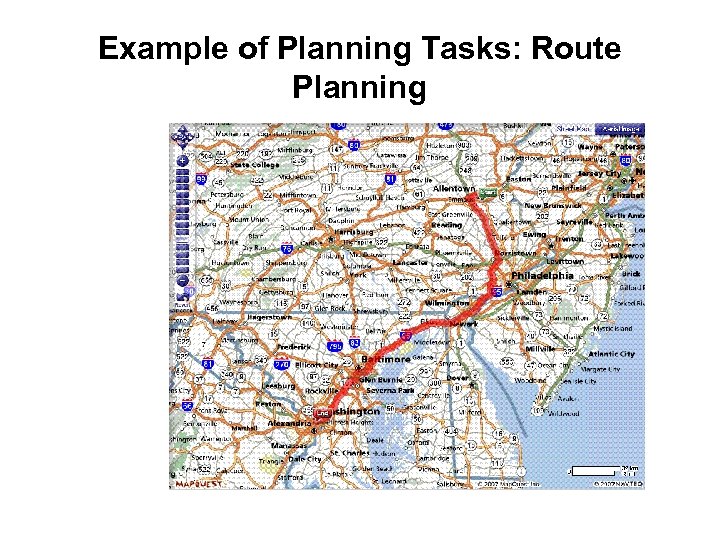Example of Planning Tasks: Route Planning

Classical Planning • Classical planning makes a number of assumptions: Ø Symbolic information (i. e. , non numerical) Ø Actions always succeed Ø The “Strips” assumption: only changes that takes place are those indicated by the operators Ø Next slide enumerates all assumptions • Despite these (admittedly unrealistic) assumptions some work-around can be made (and have been made!) to apply the principles of classical planning to games • “Hot” research topic: to removes some of these assumptions

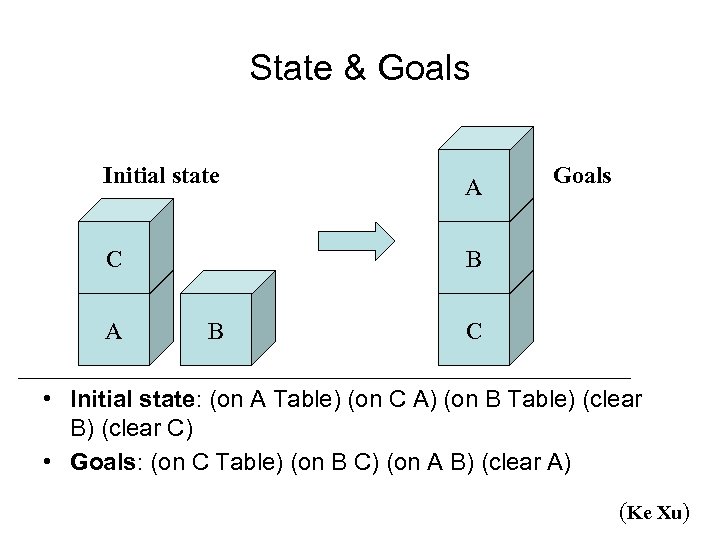State & Goals Initial state A C B A B Goals C • Initial state: (on A Table) (on C A) (on B Table) (clear B) (clear C) • Goals: (on C Table) (on B C) (on A B) (clear A) (Ke Xu)

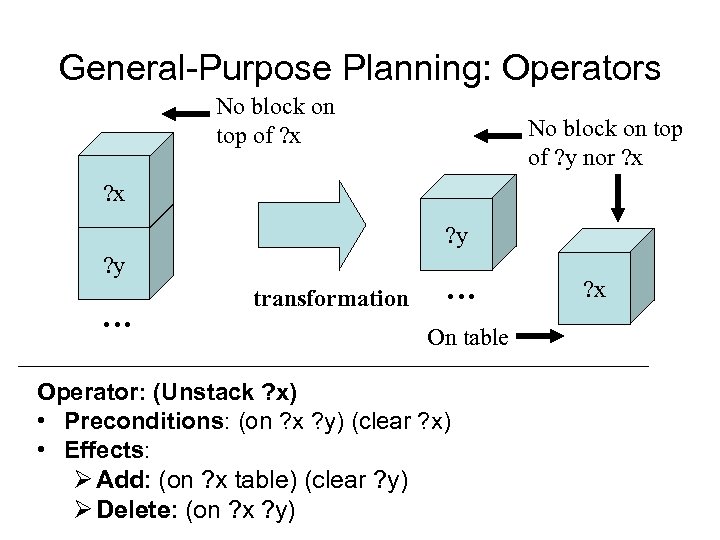General-Purpose Planning: Operators No block on top of ? x No block on top of ? y nor ? x ? y … transformation … On table Operator: (Unstack ? x) • Preconditions: (on ? x ? y) (clear ? x) • Effects: Ø Add: (on ? x table) (clear ? y) Ø Delete: (on ? x ? y) ? x

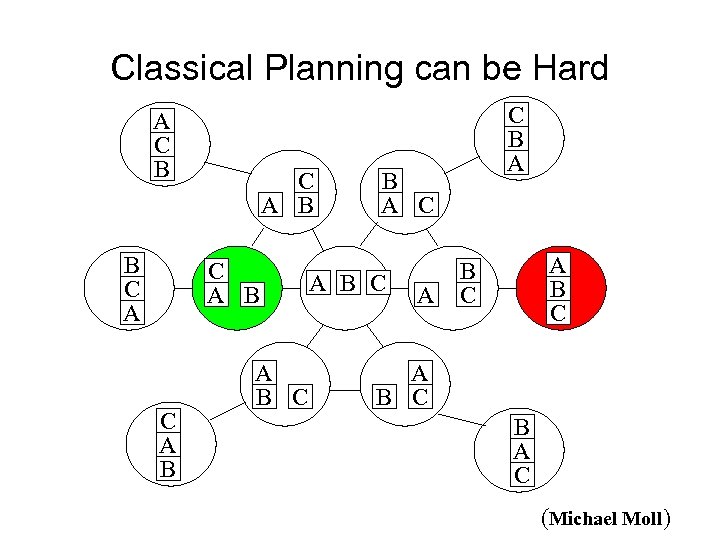Classical Planning can be Hard A C B B C A B A B C C B A C A B C A B C B A C (Michael Moll)

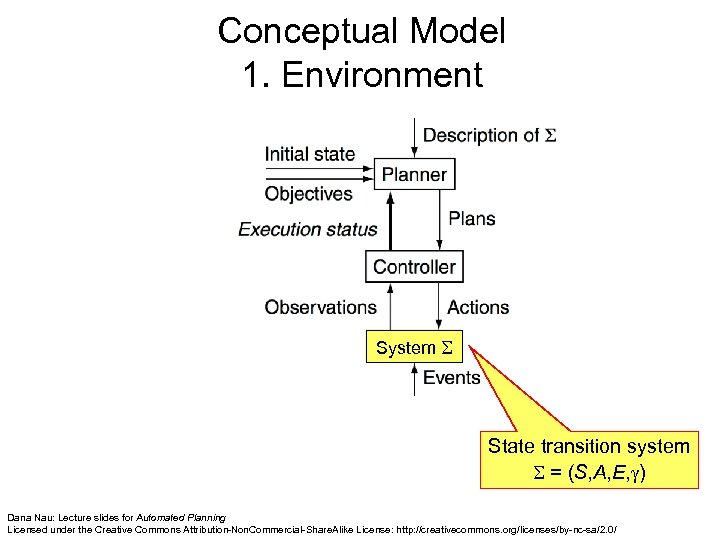Conceptual Model 1. Environment System State transition system = (S, A, E, ) Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

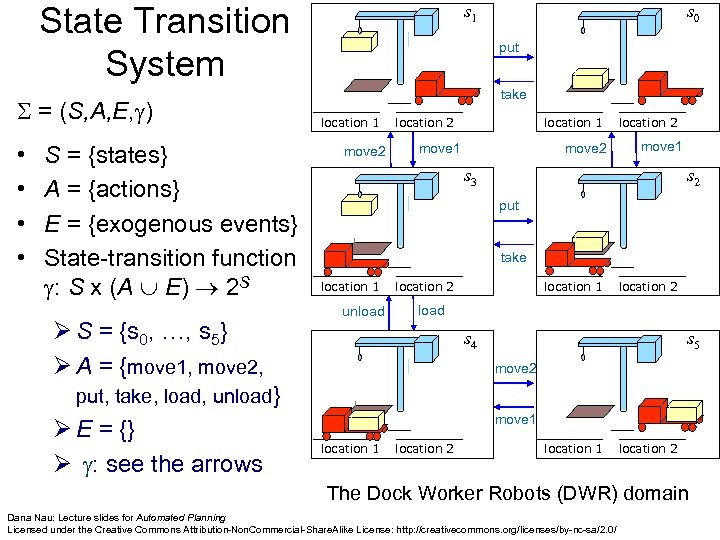State Transition System = (S, A, E, ) • • S = {states} A = {actions} E = {exogenous events} State-transition function : S x (A E) 2 S Ø S = {s 0, …, s 5} Ø A = {move 1, move 2, s 1 s 0 put take location 1 move 2 move 1 location 2 move 1 s 3 s 2 put take location 1 unload location 2 location 1 location 2 load s 4 s 5 move 2 put, take, load, unload} Ø E = {} Ø : see the arrows move 1 location 2 location 1 location 2 The Dock Worker Robots (DWR) domain Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

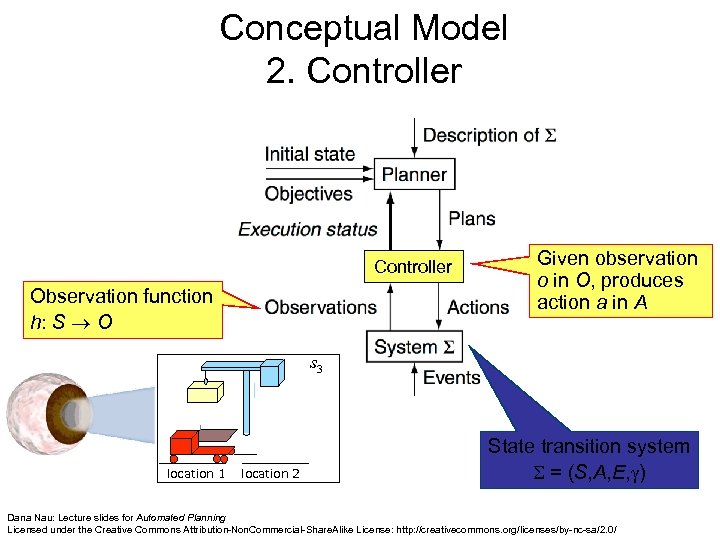Conceptual Model 2. Controller Observation function h: S O Given observation o in O, produces action a in A s 3 location 1 location 2 State transition system = (S, A, E, ) Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

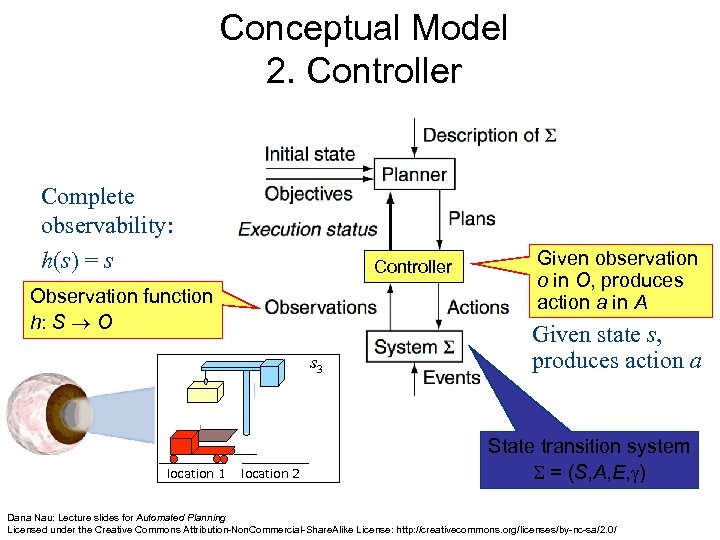Conceptual Model 2. Controller Complete observability: h(s) = s Controller Observation function h: S O s 3 location 1 location 2 Given observation o in O, produces action a in A Given state s, produces action a State transition system = (S, A, E, ) Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

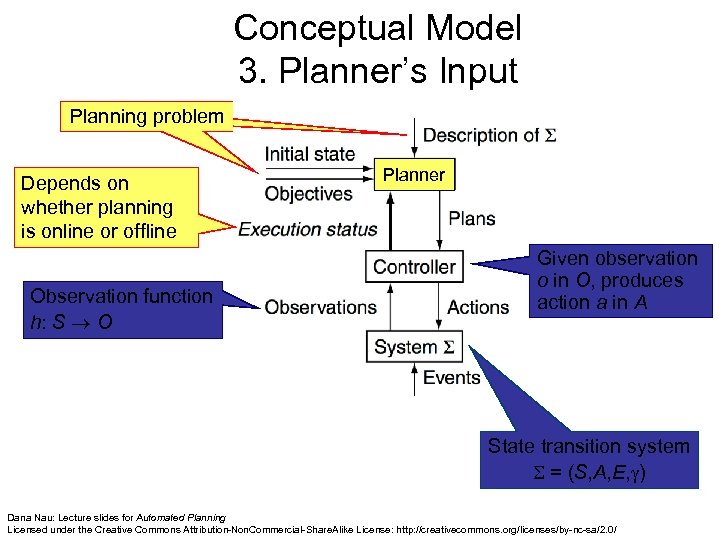Conceptual Model 3. Planner’s Input Planning problem Depends on whether planning is online or offline Observation function h: S O Planner Given observation o in O, produces action a in A State transition system = (S, A, E, ) Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

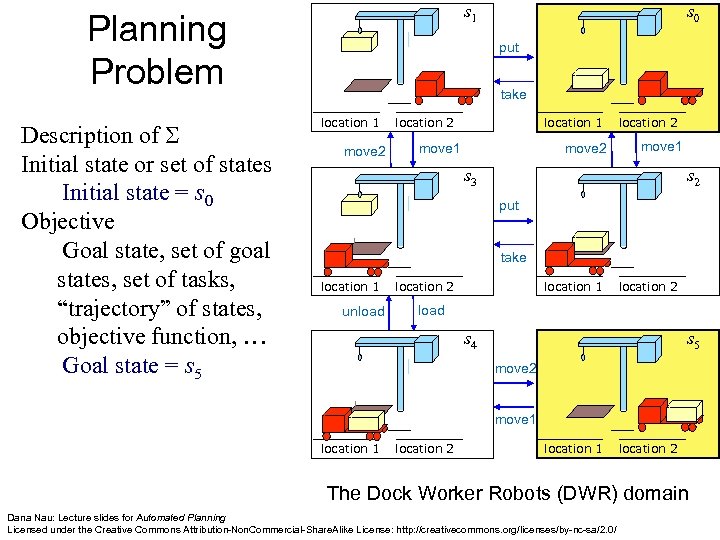s 1 Planning Problem Description of Initial state or set of states Initial state = s 0 Objective Goal state, set of goal states, set of tasks, “trajectory” of states, objective function, … Goal state = s 5 s 0 put take location 1 move 2 move 1 location 2 move 1 s 3 s 2 put take location 1 unload location 2 location 1 location 2 load s 4 s 5 move 2 move 1 location 2 location 1 location 2 The Dock Worker Robots (DWR) domain Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

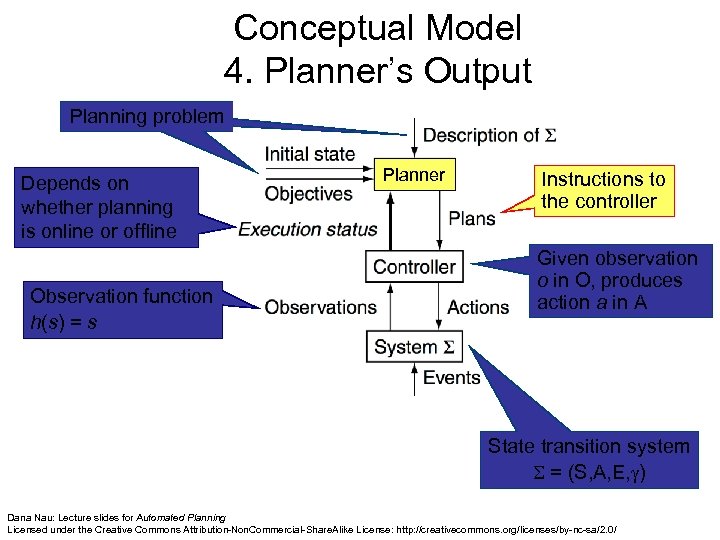Conceptual Model 4. Planner’s Output Planning problem Depends on whether planning is online or offline Observation function h(s) = s Planner Instructions to the controller Given observation o in O, produces action a in A State transition system = (S, A, E, ) Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

Classical Assumptions (I) • A 0: Finite system Ø finitely many states, actions, and events • A 1: Fully observable Ø the controller always knows what state is in • A 2: Deterministic Ø each action or event has only one possible outcome • A 3: Static Ø No exogenous events: no changes except those performed by the controller Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

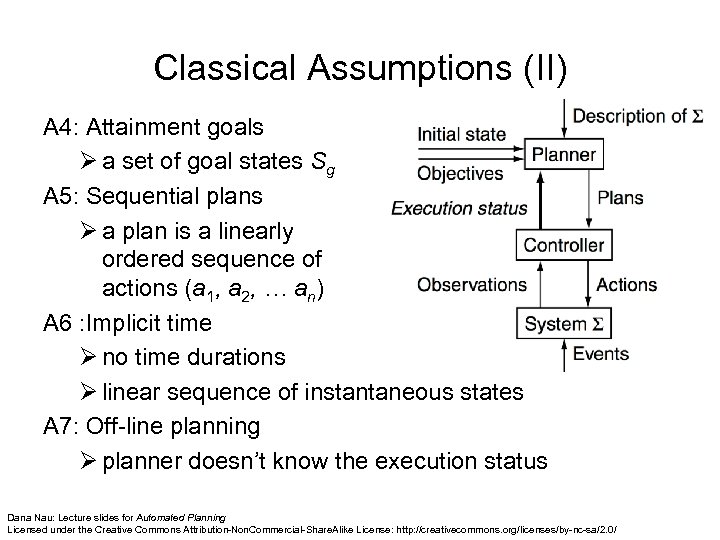Classical Assumptions (II) A 4: Attainment goals Ø a set of goal states Sg A 5: Sequential plans Ø a plan is a linearly ordered sequence of actions (a 1, a 2, … an) A 6 : Implicit time Ø no time durations Ø linear sequence of instantaneous states A 7: Off-line planning Ø planner doesn’t know the execution status Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/

This is Nice but How About Actual Deployed Applications? • We briefly discuss three deployed applications: Ø Fear: application of a “classical” planner Ø Bridge: application of a “new-classical” planner Ø MRB: planning + execution • We will discuss these again in detail later in the semester

Detailed Discussion of Topics • See web page

Math Background: Logic Source: Appendix B. 3

Introduction to Logic • A logic is a formal system of representing knowledge • A logic has: Ø Syntax – indicates the valid expressions Ø Semantics – provides meaning to the expressions Ø Inference mechanism – draw conclusions from a set of statements

Example: propositional Logic Definition. A propositonal formula is defined recursively as follows: • A symbol form a predefined list P is a proposition • If 1 and 2, are propositions then: Ø ( 1 2) are also propositions • If is a proposition then ¬( ) is a proposition Example. (a) (¬a ¬b c d) (¬c ¬d) (¬d) Semantics. Truth tables Inference mechanism. Modus ponens

Predicate Logic • Definition. A term is defined as follows: Ø A constant is a term Ø A variable is a term Ø If t 1, …, tn are terms and f is a function symbols then f(t 1, …, tn) is a term • Definition. If t 1, …, tn are terms and p is a symbol for an n-ary predicate then p(t 1, …, tn ) are predicates

Predicate Logic: Formulas Definition. An atomic formula is defined recursively as follows: • An atom is an atomic formula • If 1 and 2, are atomic formulas then: Ø ( 1 2) are also atomic formulas • If is a atomic formula then ¬( ) is an atomic formula • If is a atomic formula and x is a variable then: • x( ) is an atomic formula Example: x (likes(Mephistus, x) evil. Thing(x)) How do we say that Mephistus likes only evil things?

Predicate Logic: Semantics Ø ( 1 2) ج( ) Ø x( )

Predicate Logic: Literals and Clauses • Definition. A literal is an atomic formula consisting of a single atom and no quantifiers Ø likes(Mephistus, x) Ø ¬ evil. Thing(x) • Definition. A clause is a disjunction of literals Ø likes(Mephistus, x) ¬ evil. Thing(x)

Resolution: Inference Mechanism for Predicate Logic • Substitution, • Unification ØMost general unifier • Resolution: Given two clauses: • L = l 1 l 2 … ln • M = m 1 m 2 … mn If there is and li and mk such that: • li = a and mk = ¬a’ and • There is a most general unifier for a and a’ Then: ( L – li) ( M – mk) is a resolvent of L and M • Idea behind the resolution procedure