3abe8a6be9269688901d55baa047fd4e.ppt
- Количество слайдов: 30

Automated Planning and Decision Making Prof. Ronen Brafman Partial Order Planning Based on slides by: Carmel Domshlak Automated Planning and Decision Making 2007 1

Good article for this topic: § An Introduction to Least Commitment Planning – AI Magazine - Dan Weld Automated Planning and Decision Making 2

State Space Search § So far we have considered planning as search in state space ○ Forward - build a plan in the same order that it is executed ○ Backward - build a plan in the reverse order of its execution C C A B B Automated Planning and Decision Making A 3
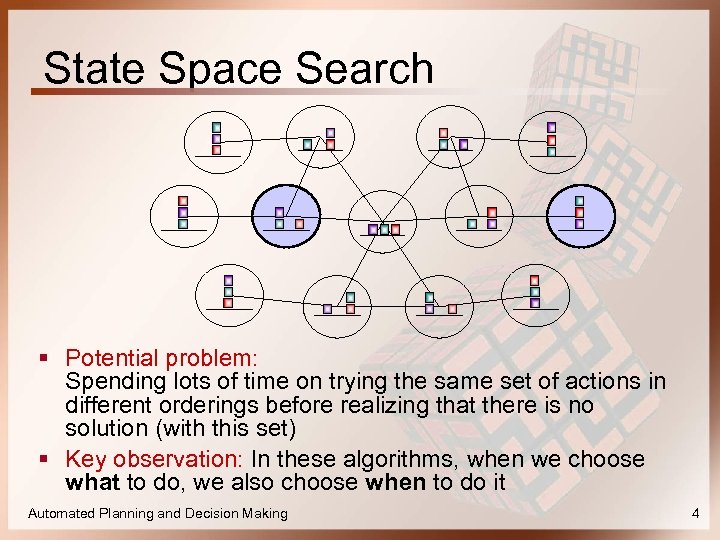
State Space Search § Potential problem: Spending lots of time on trying the same set of actions in different orderings before realizing that there is no solution (with this set) § Key observation: In these algorithms, when we choose what to do, we also choose when to do it Automated Planning and Decision Making 4
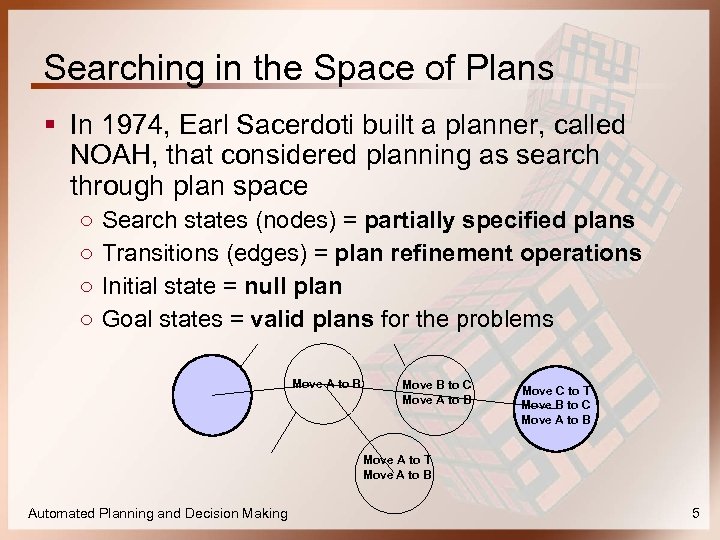
Searching in the Space of Plans § In 1974, Earl Sacerdoti built a planner, called NOAH, that considered planning as search through plan space ○ ○ Search states (nodes) = partially specified plans Transitions (edges) = plan refinement operations Initial state = null plan Goal states = valid plans for the problems Move A to B Move B to C Move A to B Move C to T Move B to C Move A to B Move A to T Move A to B Automated Planning and Decision Making 5

State Space vs. Plan Space Search through plan space -- then what is a plan? § Answer I: Totally ordered sequences of actions (or metaactions) ○ But then search through state space is isomorphic to search through plan space! ○ So what is the point of introducing “search through plan space”? ? § Answer II: Opens the road to more interesting plan representations and more interesting operators on plans, in particular, partially ordered sequence of actions Automated Planning and Decision Making 6

Least Commitment Planning § Think how you might solve a planning problem of going for a vacation in Italy ○ Need to purchase plane tickets ○ Need to buy the “Lonely Planet” guide to Italy BUT there is no need to decide (yet) which purchase should be done first Least Commitment Planning § Represent plans in a flexible way that enables deferring decisions § At the planning phase, only the essential ordering decisions are recorded Automated Planning and Decision Making 7

Partial-Order Plans § Given a Strips task Π = (P, A, I, G) we search through a space of hypothetical partial-order plans § A plan (= search node) is a triplet: <A, O, L> in which ○ A is a set of actions from A, possibly with (labeled) repetitions ○ O is a set of ordering constraints over A ○ L is a set of causal links (a bit later) § Example: A = {a 1, a 2, a 3}, O = {a 1 < a 3, a 2 < a 3} § Observe: Planner must (eventually) ensure the consistency of O. Automated Planning and Decision Making 8

Causal Links A key aspect of least commitment planning: keep track of past decisions and the reasons for those decisions § If you purchase plane tickets early to board the plane, make sure they’re with you when you get to the airport § If another goal causes you to drop the tickets (e. g. , having your hands free to open the taxi door), then you should be sure to pick them up again. § A good way to reason about and ensure non-interference between different actions introduced into the plan is to record dependencies between actions explicitly § Causal links ap q ac records our decision to use ap to produce the precondition q of ac Automated Planning and Decision Making 9

Threats § Causal links are used to detect when a newly introduced action interferes with past decisions. § Such an action is called a threat § Suppose that ○ ap q ac is a causal link in L (of some plan<A, O, L>) ○ at is yet another action in A § We say that at threatens ap q ac if ○ O U {ap < at < ac} is consistent, and ○ q ∈ del(at) Automated Planning and Decision Making 10

Eliminating Threats § When a plan contains a threat, then it is possible that the plan would not work as anticipated. ○ Which means what? § Solution: identify threats and take evasive countermeasures ○ promotion by O U= {at > ac} ○ demotion by O U= {at < ap} ○. . . Automated Planning and Decision Making 11

Planning Problems as Null Plans Uniformity is the key to simplicity § Can use the same structure to represent both the planning problem and complete plans § Planning problem as a null plan <A, O, L> where ○ A = {a 0, a 1}, O = {a 0 < a 1}, L = {} ○ pre(a 0) = {}, del(a 0) = {}, add(a 0) = I ○ pre(a 1) = G, del(a 1) = {}, add(a 1) = {} *start* (on c a) (clear b) (clear c) (on a table)(on b table) (on a b) (on b c) *end* Automated Planning and Decision Making 12

The POP Algorithm Schematic description Regressive algorithm that searches plan space § Starts with the null plan § Makes non-deterministic plan refinement choices until ○ all preconditions of all actions in the plan have been supported by causal links, and ○ all threats against any causal link have been removed Automated Planning and Decision Making 13

The POP Algorithm Input and Output § Recursive calls to POP with POP(<A, O, L>, agenda, A) where ○ <A, O, L> is a plan structure ○ agenda is a list of “open goals” that need to be supported by causal links ○ A is the action set of our Strips problem § Initial call is with ○ null plan <{a 0, a∞}, {a 0 < a∞}, {}> ○ agenda = {(g, a∞) | g ∈ pre(a∞) ≡ G} If <A, O, L> is outputted by POP, then any total ordering of actions A consistent with O is a valid plan for our problem. Automated Planning and Decision Making 14

The POP Algorithm POP(<A, O, L>, agenda, A) § Termination: if agenda = Ø then return <A, O, L> § Goal selection: choose (q, aneed ) ∈ agenda § Action selection… Automated Planning and Decision Making 15

The POP Algorithm § Action selection: ○ choose action aadd (either from A, or from A) such that • q ∈ add(aadd), and • O U {aadd < aneed} is consistent ○ if no such action then return FALSE ○ otherwise • L U= {aadd q aneed} and O U= {aadd < aneed} • if aadd is a new action instance then A U= {aadd}, and O U= {a 0 < aadd < a 1} § Update goal set: ○ agenda = {(q, aneed)} ○ if aadd was a new action instance then agenda U= {(r , aadd) | r ∈ pre(aadd)} Automated Planning and Decision Making 16

The POP Algorithm POP(<A, O, L>, agenda, A) § Termination: if agenda = Ø then return <A, O, L> § Goal selection: choose (q, aneed ) ∈ agenda § Action selection: choose and process aadd. . . § Update goal set: add preconditions of aadd to the agenda. . . § Causal link protection: foreach causal link {ap q ac} ∈ L, and at threatens it ○ choose either O U= {at > ac}, or O U= {at < ap} ○ if neither constraint is consistent, then return FALSE § Recursive invocation: POP(<A, O, L>, agenda, A) Automated Planning and Decision Making 17

The POP Algorithm In one slide. . . POP(<A, O, L>, agenda, A) § Termination: if agenda = Ø then return <A, O, L> § Goal selection: choose (q, aneed ) ∈ agenda § Action selection: ○ choose action aadd (either from A, or from A) such that • q ∈ add(aadd), and • O U {aadd < aneed} is consistent ○ if no such action then return FALSE ○ otherwise • L U= {aadd q aneed} and O U= {aadd < aneed} • if aadd is a new action instance then A U= {aadd}, and O U= {a 0 < aadd < a 1} § Update goal set: ○ agenda = {(q, aneed)} ○ if aadd was a new action instance then agenda U= {(r , aadd) | r ∈ pre(aadd)} § Causal link protection: foreach causal link {ap ○ ○ § q ac} ∈ L, and at threatens it choose either O U= {at > ac}, or O U= {at < ap} if neither constraint is consistent, then return FALSE Recursive invocation: POP(<A, O, L>, agenda, A) Automated Planning and Decision Making 18

Choice Points Three choice points § Goal selection § Action selection § Causal link protection How crucial these choices are? § Affect soundness? § Affect completeness? § Affect efficiency? Automated Planning and Decision Making 19

Example - Step 1 C A B Initial call to POP with § Null Plan (see the right figure) § agenda = {(on. AB, a∞) , (on. BC, a∞)} First choice is goal selection § Affects efficiency, but not completeness! Automated Planning and Decision Making 20

Example - Step 2 Suppose (on. BC, a∞) is selected (i. e. , aneed = a∞) § Need to choose an action aadd that will provide on. BC ○ This is a real non-deterministic choice! Suppose that an oracle suggests making aadd a new instance of the action move-B-from-Table-to-C ○ a causal link aadd on. BC a∞ is added to L ○ agenda is properly updated (how exactly? ) ○ no threats to resolve. . . recursive call Automated Planning and Decision Making 21

Example - Step 2 Suppose that an oracle suggests making aadd a new instance of the action move-B-from-Table-to-C ○ a causal link aadd on. BC a∞ is added to L ○ agenda is properly updated (how exactly? ) ○ no threats to resolve. . . recursive call *start* (on c a) (clear b) (clear c) (on a table) (on b table) (clear b) (clear c) (on b table) (move b from table to c) (clear table) ¬(on b table) ¬(clear c) (on b c) (on a b) (on b c) *end* Automated Planning and Decision Making 22

Example - Step 3 Suppose (clear. B, move-B-from-Table-to-C) is selected § Oracle suggests to reuse an existing action instance a 0 ○ add a causal link a 0 clear. B move-B-from-Table-to-C ○ agenda is properly updated (how exactly? ) ○ no threats to resolve. . . recursive call *start* (on c a) (clear b) (clear c) (on a table) (on b table) (clear b) (clear c) (on b table) (move b from table to c) (clear table) ¬(on b table) ¬(clear c) (on b c) (on a b) (on b c) Automated Planning and Decision Making *end* 23

Example - Step 4 a § § § Suppose (on. AB, a∞) is selected Oracle suggests making aadd be a new instance of the action move-A-from. Table-to-B, and we do that. . . BUT this time we have a threat! ○ move-A-from-Table-to-B and move-B-from-Table-to-C have no constraints on their relative ordering ○ move-A-from-Table-to-B deletes clear. B that is required by move-B-from-Table-to-C *start* (on c a) (clear b) (clear c) (on a table) (on b table) (clear b) (clear a) (on a table) (clear b) (clear c) (on b table) (move a from table to b) (move b from table to c) (on a b) (clear table) ¬(on a table) ¬(clear b) (clear table) ¬(on b table) ¬(clear c) (on b c) (on a b) (on b c) *end* Automated Planning and Decision Making 24

Example - Step 4 b Try to protect the causal link a 0 clear. B move-B-from-Table-to-C § In general, there are two options — promotion and demotion — and this is a true non-deterministic choice! § In our example, demotion is inconsistent (why? ), but promotion is OK *start* (on c a) (clear b) (clear c) (on a table) (on b table) (clear b) (clear c) (on b table) (clear b) (clear a) (on a table) (move b from table to c) (move a from table to b) (clear table) ¬(on b table) ¬(clear c) (on b c) (on a b) (clear table) ¬(on a table) ¬(clear b) (on a b) (on b c) *end* Automated Planning and Decision Making 25
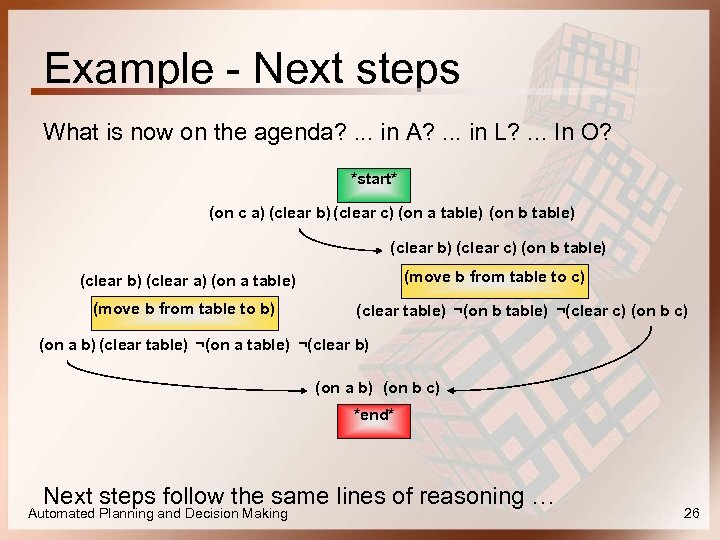
Example - Next steps What is now on the agenda? . . . in A? . . . in L? . . . In O? *start* (on c a) (clear b) (clear c) (on a table) (on b table) (clear b) (clear c) (on b table) (move b from table to c) (clear b) (clear a) (on a table) (move b from table to b) (clear table) ¬(on b table) ¬(clear c) (on b c) (on a b) (clear table) ¬(on a table) ¬(clear b) (on a b) (on b c) *end* Next steps follow the same lines of reasoning … Automated Planning and Decision Making 26
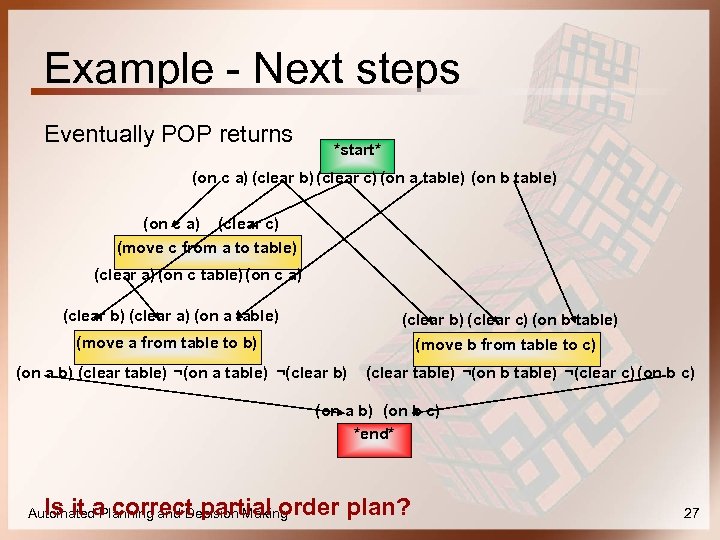
Example - Next steps Eventually POP returns *start* (on c a) (clear b) (clear c) (on a table) (on b table) (on c a) (clear c) (move c from a to table) (clear a) (on c table) (on c a) (clear b) (clear a) (on a table) (clear b) (clear c) (on b table) (move a from table to b) (move b from table to c) (on a b) (clear table) ¬(on a table) ¬(clear b) (clear table) ¬(on b table) ¬(clear c) (on b c) (on a b) (on b c) *end* Is it a correct partial order plan? Automated Planning and Decision Making 27

Advantages § Natural extension to planning with partially instantiated actions ○. . . add action instance move(A, x, B) ○. . . postpone unifying ? x with a concrete object until necessary § Natural extensions to more complex action formalisms ○. . . action durations ○. . . delayed effects ○. . . § Least commitment may lead to shorter search times ○ Mainly due to smaller branching factor § Another way of viewing it: constraint-based planning Automated Planning and Decision Making 28

Disadvantages § Significantly more complex algorithm ○. . . higher per-node cost § Hard to determine what is true in a state ○. . . harder to devise informed heuristics (for all three types of choices) ○. . . how to prune infinitely long paths? ? Automated Planning and Decision Making 29

Literature 1. D. Weld, An Introduction to Least Commitment Planning, AI Magazine, 1994. 2. J. S. Penberthy and D. Weld, UCPOP: A sound, complete, partial order planner for ADL, KR, 1992. 3. . for many more, see, e. g. , bibliography in (1) Automated Planning and Decision Making 30
3abe8a6be9269688901d55baa047fd4e.ppt