Aulas Multimídias Santa Cecília Profº Israel Lopes

Aulas Multimídias – Santa Cecília Profº Israel Lopes

C ítu ap 7: lo tas Re pl co are an pág s( 7). 8

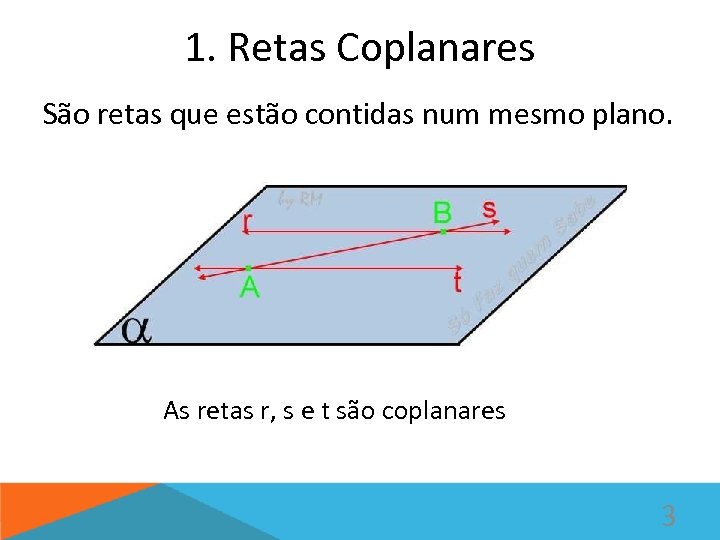1. Retas Coplanares São retas que estão contidas num mesmo plano. As retas r, s e t são coplanares 3

2. Posições relativas de duas retas 1. Concorrentes: possuem um ponto em comum Obs. : t x s 2. Paralelas: não têm nenhum ponto em comum Obs. : r // s 4

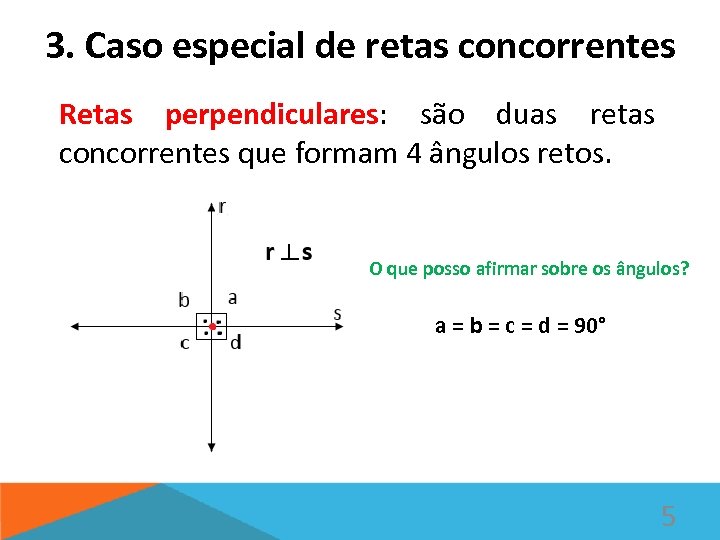3. Caso especial de retas concorrentes Retas perpendiculares: são duas retas concorrentes que formam 4 ângulos retos. O que posso afirmar sobre os ângulos? a = b = c = d = 90° 5

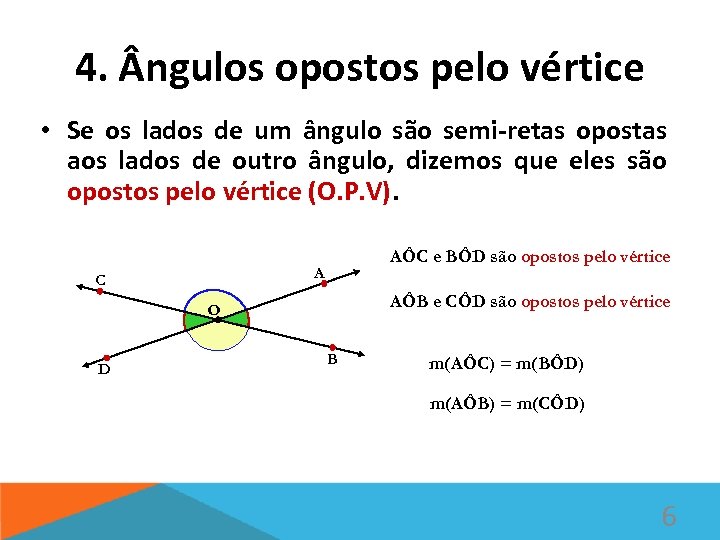4. ngulos opostos pelo vértice • Se os lados de um ângulo são semi-retas opostas aos lados de outro ângulo, dizemos que eles são opostos pelo vértice (O. P. V). AÔC e BÔD são opostos pelo vértice A C AÔB e CÔD são opostos pelo vértice O D B m(AÔC) = m(BÔD) m(AÔB) = m(CÔD) 6

Exemplo: Determine a medida de cada ângulo descrito a seguir: 1) Determinando o valor de x: 6 x + 5° = 8 x – 10° - 2 x = -15° - X = -7, 5° x(-1) X = 7, 5° 2) Determinando o valor do ângulo: 6 x + 5° Substituo x por 7, 5° 6. 7, 5° + 5° = 50° 3) Portanto, cada ângulo OPV mede 50°. 7

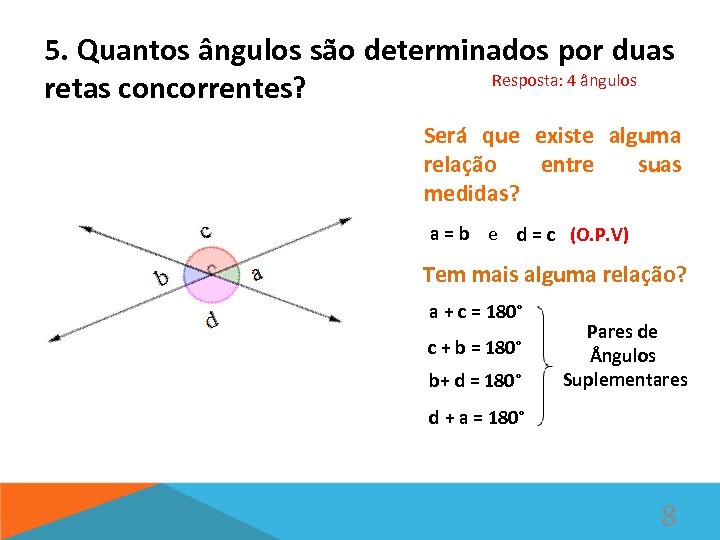5. Quantos ângulos são determinados por duas Resposta: 4 ângulos retas concorrentes? Será que existe alguma relação entre suas medidas? a = b e d = c (O. P. V) Tem mais alguma relação? a + c = 180° c + b = 180° b+ d = 180° Pares de ngulos Suplementares d + a = 180° 8

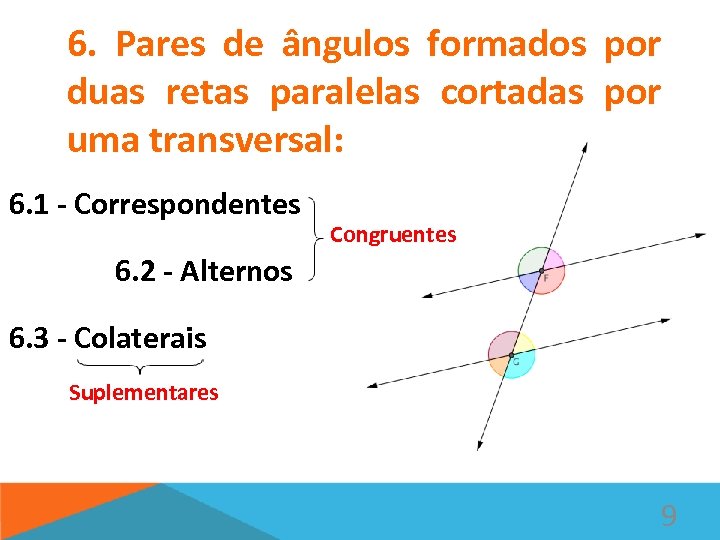6. Pares de ângulos formados por duas retas paralelas cortadas por uma transversal: 6. 1 - Correspondentes Congruentes 6. 2 - Alternos 6. 3 - Colaterais Suplementares 9

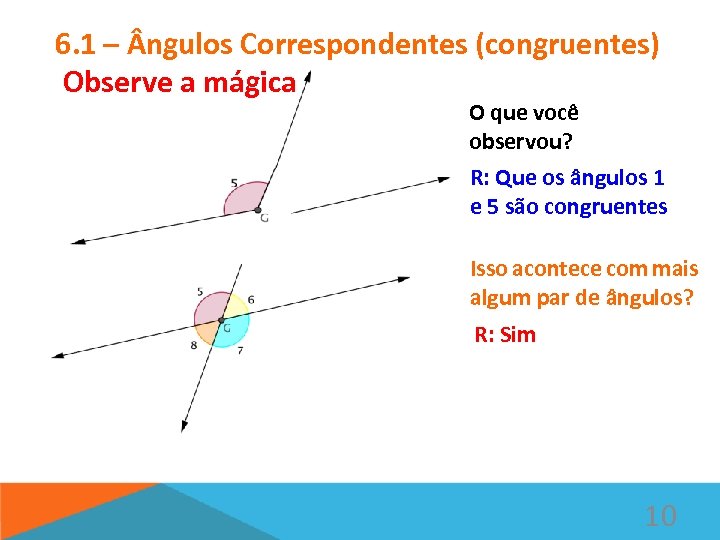6. 1 – ngulos Correspondentes (congruentes) Observe a mágica O que você observou? R: Que os ângulos 1 e 5 são congruentes Isso acontece com mais algum par de ângulos? R: Sim 10

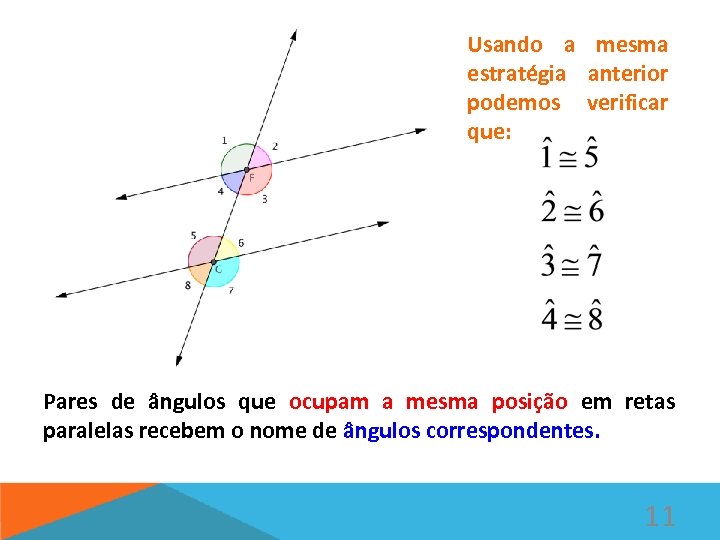Usando a mesma estratégia anterior podemos verificar que: Pares de ângulos que ocupam a mesma posição em retas paralelas recebem o nome de ângulos correspondentes. 11

6. 2 – ngulos Alternos (Congruentes) São ângulos que estão em lados contrários na reta transversal. • Alternos Internos 4 e 6 3 e 5 Internos: estão entre as paralelas. Externos: paralelas. estão • Alternos Externos 1 e 7 2 e 8 fora das 12

6. 3 – ngulos Colaterais (Suplementares) Porque estão em um mesmo lado da reta transversal. Os ângulos colaterais podem ser internos e externos. • Internos: Estão entre as paralelas. • Externos: Estão fora das paralelas. 13

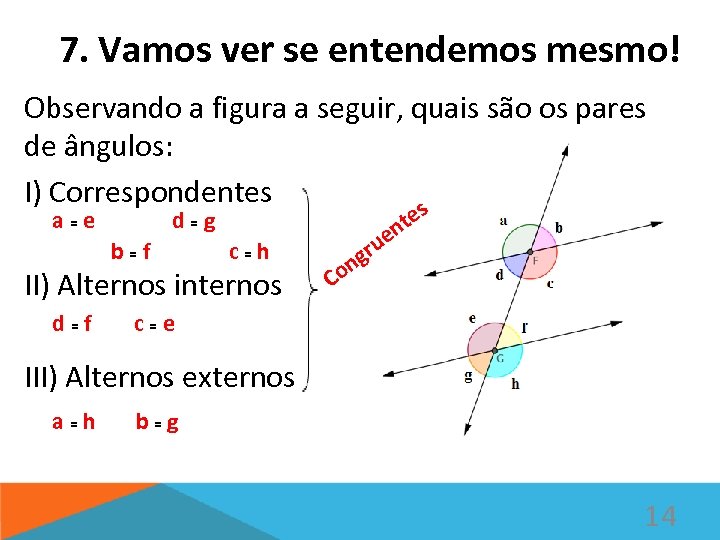7. Vamos ver se entendemos mesmo! Observando a figura a seguir, quais são os pares de ângulos: I) Correspondentes s a=e d=g b=f II) Alternos internos d=f e ru ng o c=h te n C c=e III) Alternos externos a=h b=g 14

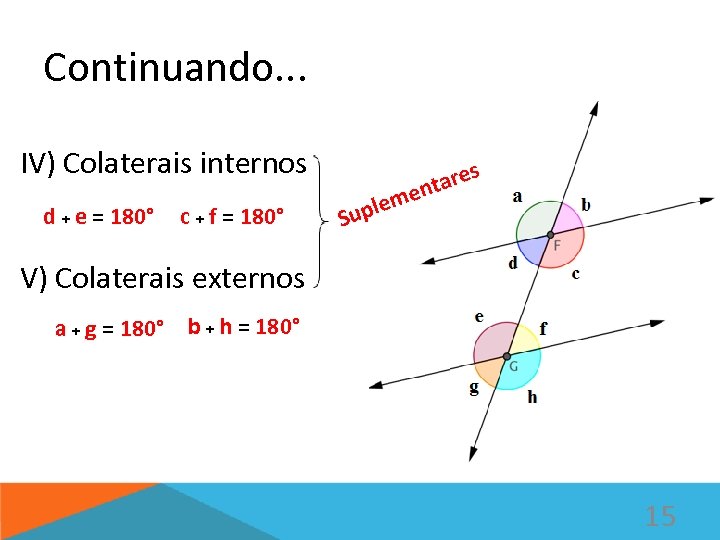Continuando. . . IV) Colaterais internos d + e = 180° c + f = 180° ares ent m le Sup V) Colaterais externos a + g = 180° b + h = 180° 15

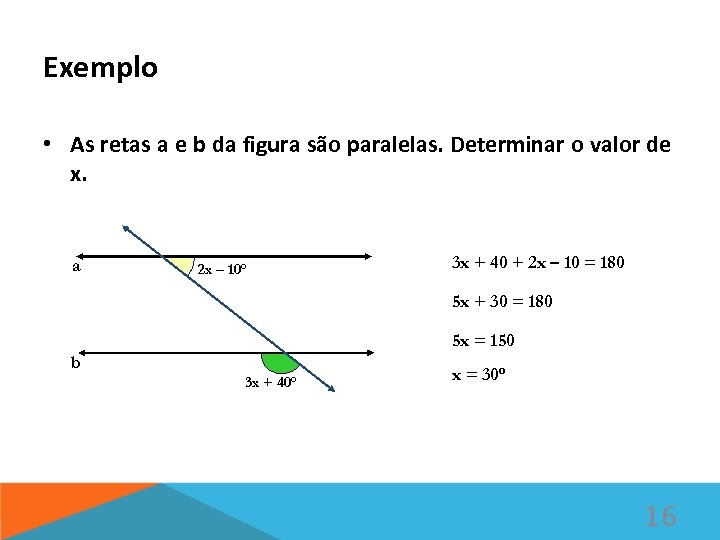Exemplo • As retas a e b da figura são paralelas. Determinar o valor de x. a 2 x – 10º 3 x + 40 + 2 x – 10 = 180 5 x + 30 = 180 5 x = 150 b 3 x + 40º x = 30º 16

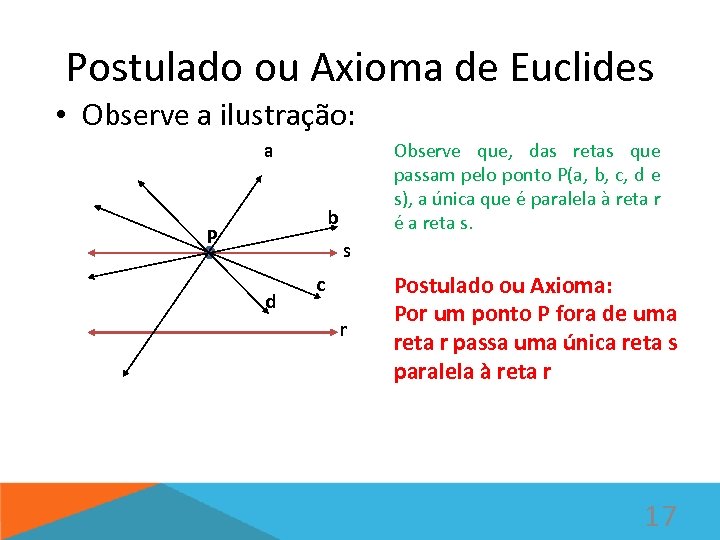Postulado ou Axioma de Euclides • Observe a ilustração: a Observe que, das retas que passam pelo ponto P(a, b, c, d e s), a única que é paralela à reta r é a reta s. b P s d c r Postulado ou Axioma: Por um ponto P fora de uma reta r passa uma única reta s paralela à reta r 17

Créditos Imagem 1: Richard Megna / Fundamental Photographs / Universal Images Group https: //quest. eb. com/#/search/angulos/1/157_2927159/REFLECTION-OF-LASER -BEAMS-BY-PLANE-MIRROR-Angle-Of-Incidence Rede de Ensino Pitágoras Israel Lopes