244508103304b27e0776b3c45bc64ba3.ppt
- Количество слайдов: 27
 Attempts to find an optimum solution penalty value for certain classes of NP-Hard problems George M. White SITE University of Ottawa white@site. uottawa. ca CORS - Ottawa
Attempts to find an optimum solution penalty value for certain classes of NP-Hard problems George M. White SITE University of Ottawa white@site. uottawa. ca CORS - Ottawa
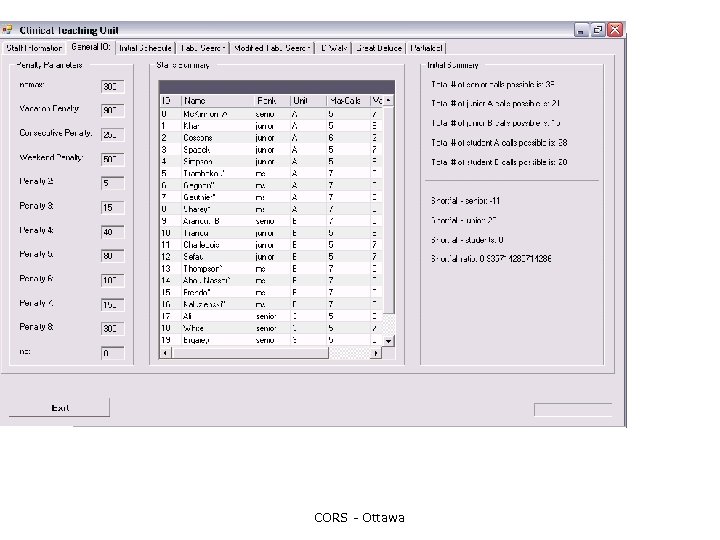
 Examples of very difficult problems medical personnel in hospitals ¡ contact centre personnel ¡ judicial staff assignments ¡ examination scheduling ¡ portfolio management ¡ CORS - Ottawa
Examples of very difficult problems medical personnel in hospitals ¡ contact centre personnel ¡ judicial staff assignments ¡ examination scheduling ¡ portfolio management ¡ CORS - Ottawa
 CORS - Ottawa
CORS - Ottawa
 CORS - Ottawa
CORS - Ottawa
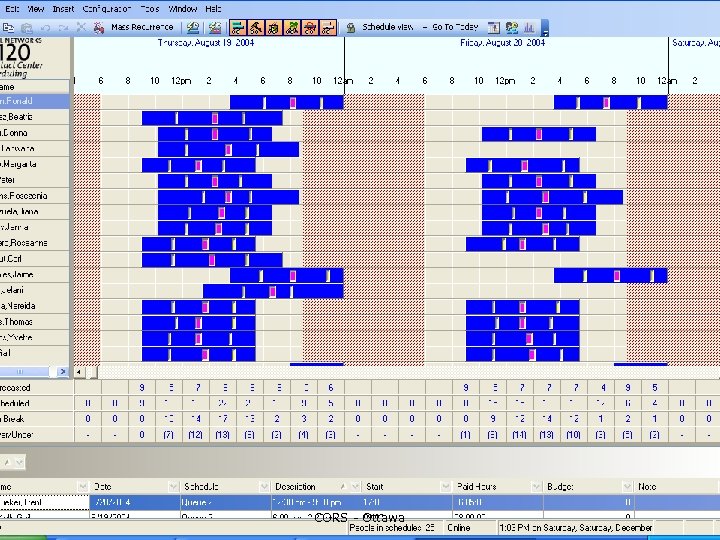
 Examples These are all examples of NP-hard assignment/scheduling problems. They are characterized by having a series of non-linear constraints ¡ We wish to find solutions such that all constraints are satisfied ¡ If this is not possible, we wish to find solutions such that a maximum number of constraints are satisfied. ¡ CORS - Ottawa
Examples These are all examples of NP-hard assignment/scheduling problems. They are characterized by having a series of non-linear constraints ¡ We wish to find solutions such that all constraints are satisfied ¡ If this is not possible, we wish to find solutions such that a maximum number of constraints are satisfied. ¡ CORS - Ottawa
 CORS - Ottawa
CORS - Ottawa
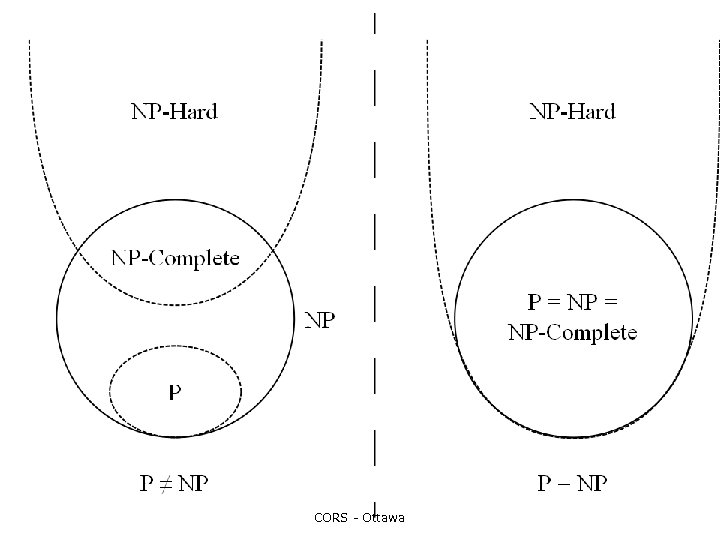
 Optimization ¡ There is often more than one possible solution. In this case we want the one that is best (i. e. we want to optimize some property of the schedule) l l total wages paid overall satisfaction personnel coverage separation CORS - Ottawa
Optimization ¡ There is often more than one possible solution. In this case we want the one that is best (i. e. we want to optimize some property of the schedule) l l total wages paid overall satisfaction personnel coverage separation CORS - Ottawa
 Optimization ¡ This implies that we must optimize some cost function(to the best value permitted by the constraints and the time available). l l unidimensional optimization multidimensional optimization CORS - Ottawa
Optimization ¡ This implies that we must optimize some cost function(to the best value permitted by the constraints and the time available). l l unidimensional optimization multidimensional optimization CORS - Ottawa
 Optimization ¡ This also means that we will have to use an approximation algorithm to find good solutions. Exact solutions require too much time for real life problems. l l l l tabu search particle swarm optimization simulated annealing great deluge partialcol IDWalk etc CORS - Ottawa
Optimization ¡ This also means that we will have to use an approximation algorithm to find good solutions. Exact solutions require too much time for real life problems. l l l l tabu search particle swarm optimization simulated annealing great deluge partialcol IDWalk etc CORS - Ottawa
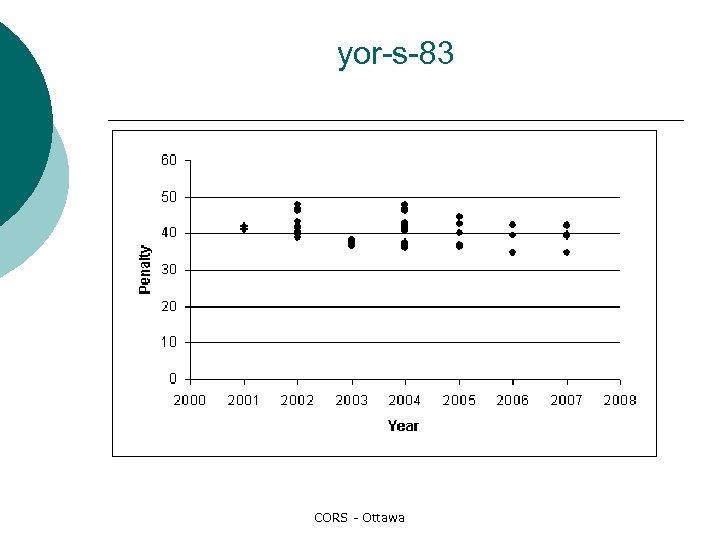 yor-s-83 CORS - Ottawa
yor-s-83 CORS - Ottawa
 yor-s-83 CORS - Ottawa
yor-s-83 CORS - Ottawa
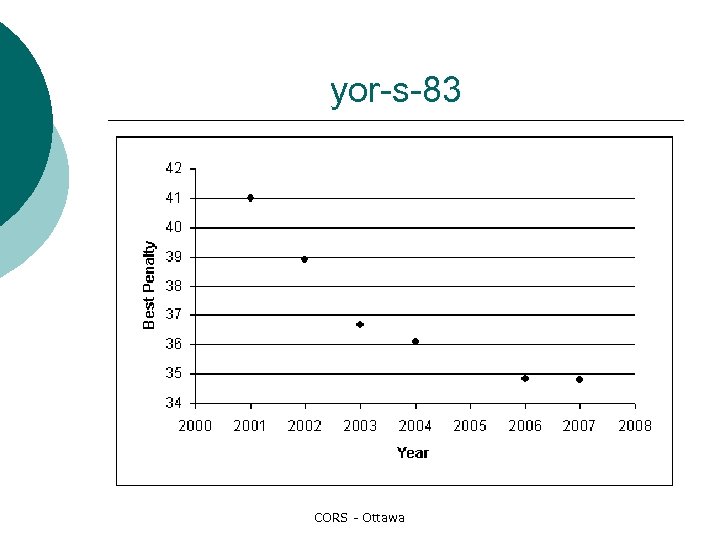
 The shape of the curve ¡ at some time in the future it seems reasonable to assume that the best penalty values will reach a limit, i. e. CORS - Ottawa
The shape of the curve ¡ at some time in the future it seems reasonable to assume that the best penalty values will reach a limit, i. e. CORS - Ottawa
 ¡ the form of d. P/dt is unknown but it is reasonable to assume that it is some function of the current penalty CORS - Ottawa
¡ the form of d. P/dt is unknown but it is reasonable to assume that it is some function of the current penalty CORS - Ottawa
 ¡ expanding this as a Maclauren series yields or CORS - Ottawa
¡ expanding this as a Maclauren series yields or CORS - Ottawa
 ¡ we want to simplify this equation as much as possible (but no further) so we try d. P/dt = a 0 ¡ this doesn’t work CORS - Ottawa
¡ we want to simplify this equation as much as possible (but no further) so we try d. P/dt = a 0 ¡ this doesn’t work CORS - Ottawa
 d. P/dt = ao + a 1 P this doesn’t work ¡ try CORS - Ottawa
d. P/dt = ao + a 1 P this doesn’t work ¡ try CORS - Ottawa
 ¡ the next simplest form is it turns out that this is a plausible form CORS - Ottawa
¡ the next simplest form is it turns out that this is a plausible form CORS - Ottawa
 ¡ at the limiting value CORS - Ottawa
¡ at the limiting value CORS - Ottawa
 and the equation is written ¡ this often appears in the literature with symbol substitution CORS - Ottawa
and the equation is written ¡ this often appears in the literature with symbol substitution CORS - Ottawa
 ¡ The solution for this equation is where P 0 = P(0) CORS - Ottawa
¡ The solution for this equation is where P 0 = P(0) CORS - Ottawa
 ¡ The limiting value of P(t) is CORS - Ottawa
¡ The limiting value of P(t) is CORS - Ottawa
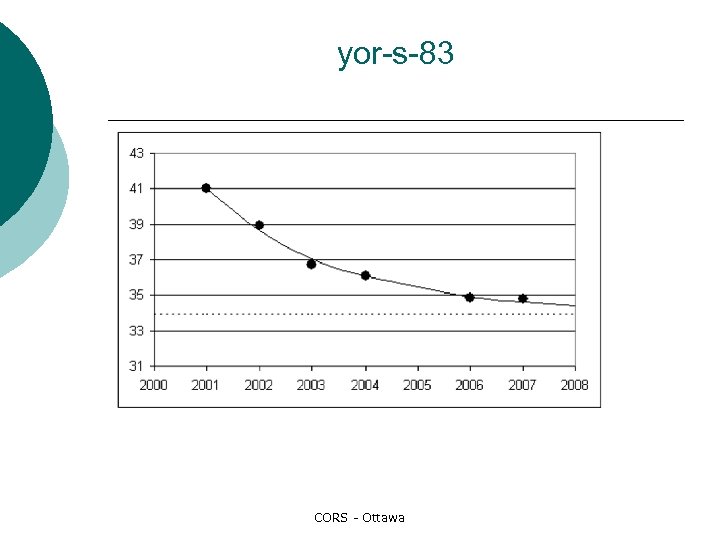
 ¡ To estimate the limiting penalty of a data set 1. 2. 3. Collect the data representing the “current champion” over time. Fit a curve to this data. Calculate the limiting value of this curve. CORS - Ottawa
¡ To estimate the limiting penalty of a data set 1. 2. 3. Collect the data representing the “current champion” over time. Fit a curve to this data. Calculate the limiting value of this curve. CORS - Ottawa
 Problems ¡ Lack of data: The largest number of points for any of the data sets is 6. Number of parameters: 3 parameters ¡ Uncertain and irregular spacing in data: ¡ Curious data points: ¡ The first (1996) data points: ¡ CORS - Ottawa
Problems ¡ Lack of data: The largest number of points for any of the data sets is 6. Number of parameters: 3 parameters ¡ Uncertain and irregular spacing in data: ¡ Curious data points: ¡ The first (1996) data points: ¡ CORS - Ottawa
 Problems ¡ Therefore, the numerical results must be regarded as preliminary estimates, subject to review as more data becomes available. CORS - Ottawa
Problems ¡ Therefore, the numerical results must be regarded as preliminary estimates, subject to review as more data becomes available. CORS - Ottawa
 yor-s-83 CORS - Ottawa
yor-s-83 CORS - Ottawa
 Similar behaviour has been observed for other data sets of the same type. Work continues on other sets of data from other real-world problems. CORS - Ottawa
Similar behaviour has been observed for other data sets of the same type. Work continues on other sets of data from other real-world problems. CORS - Ottawa
 Thank you George White white@site. uottawa. ca CORS - Ottawa
Thank you George White white@site. uottawa. ca CORS - Ottawa


