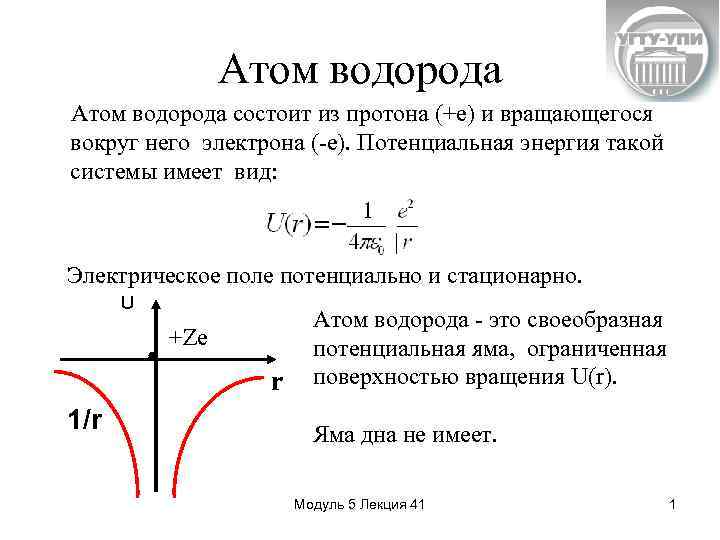
Атом водорода состоит из протона е и вращающегося

Атом водорода состоит из протона (+е) и вращающегося вокруг него электрона (-е). Потенциальная энергия такой системы имеет вид: Электрическое поле потенциально и стационарно. U +Ze r 1/r Атом водорода - это своеобразная потенциальная яма, ограниченная поверхностью вращения U(r). Яма дна не имеет. Модуль 5 Лекция 41 1

Так как движение электрона в атоме водорода происходит в пространстве, то нельзя рассматривать одномерный случай. Уравнение Шредингера имеет вид: 2 Движение электрона происходит в центральном сферическом поле, поэтому целесообразно перейти к сферическим координатам, т. е. от Ψ(x, y, z)→Ψ(r, , φ) z A(x, y, z) 0 x y Решение уравнения Шредингера ищут в виде произведения трех независимых функций: Ψ(r, , φ)= R(r)· ( )·Ф( ) Полное решение очень сложное. Ограничимся простейшим сферически симметричным, зависящим только от r - расстоянием электрона от протона. Модуль 5 Лекция 41 2

E, эв Атом водорода по квантовой механике r 0 n↑↑ Е→ 0 n=3 Е 3=-1. 51 э. В n=2 Е 2= -3. 4 э. В n=1 E 1= -13. 6 эв Энергетический спектр дискретный, сходящийся. Е <0 Модуль 5 Лекция 41 3

Квантовые числа n= 1, 2, 34, …. . – главное квантовое число квантует (определяет) энергию l = 0, 1, 2, 3. . . (n-1) – орбитальное (побочное, азимутальное), квантовое число определяет возможные значения момента импульса электрона относительно ядра. Всего n значений. Дж·с - орбитальный момент импульса l=0 l=1 l=2 l=3 l=4 s- электрон p- электрон d - электрон f - электрон g - электрон - единица квантования Модуль 5 Лекция 41 4

Pm(магн) e - единица квантования магнитного момента I L(мех) m =0, +1, +2…+ m < Всего 2 l+1 значений Магнитное орбитальное квантовое число осуществляет пространственное квантование. Оно квантует величину проекции момента импульса на некоторое выбранное преимущественное направление. Модуль 5 Лекция 41 5

Относительно преимущественного направления в пространстве (обычно направления электрического или магнитного полей) возможны лишь такие ориентации векторов механического и магнитного орбитальных моментов, чтобы их проекции на это направление принимали целочисленное значение и Зная n, l, m , можно определить квантовое состояние электрона – его энергию, импульс, момент импульса, проекцию момента импульса и другие характеристики. Модуль 5 Лекция 41 6

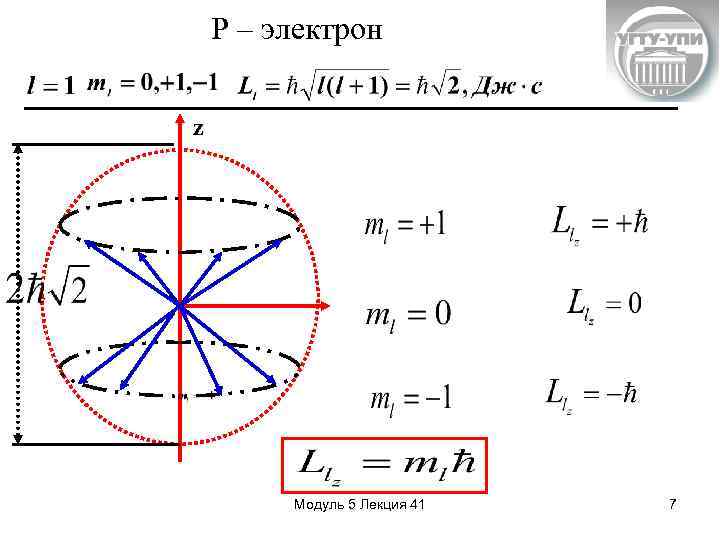Р – электрон z Модуль 5 Лекция 41 7

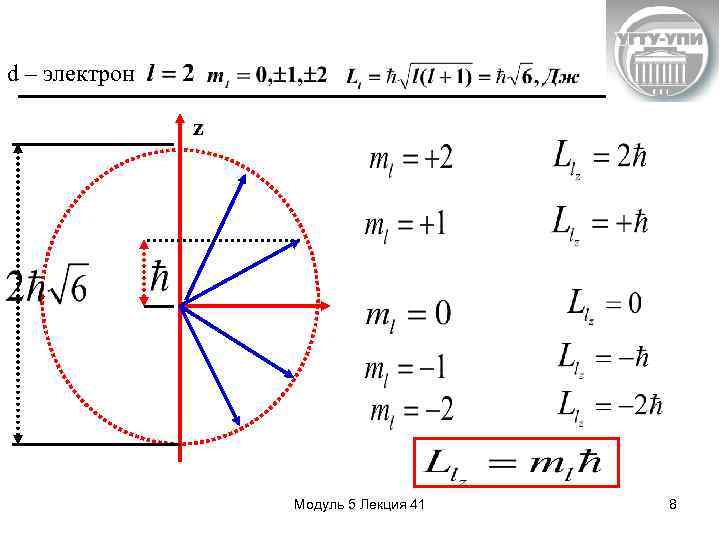d – электрон z Модуль 5 Лекция 41 8

Если известна энергия атома, то мы еще не знаем, в каком состоянии находится электрон. Пусть n=2 E=E 2 n=2 =0 m =0 =1 m =+1 =1 m =-1 4 состояния Кратность вырождения g= n 2 Модуль 5 Лекция 41 9

Различные квантовые состояния электрона в атоме, которым соответствует одна и та же энергия, называются вырожденными, а число состояний с данной энергией кратностью вырождения. Модуль 5 Лекция 41 10