10_atom_vodoroda.ppt
- Количество слайдов: 42
 Атом водорода Семинар 10
Атом водорода Семинар 10
 Раздел 1 МОДЕЛЬ АТОМА ВОДОРОДА
Раздел 1 МОДЕЛЬ АТОМА ВОДОРОДА
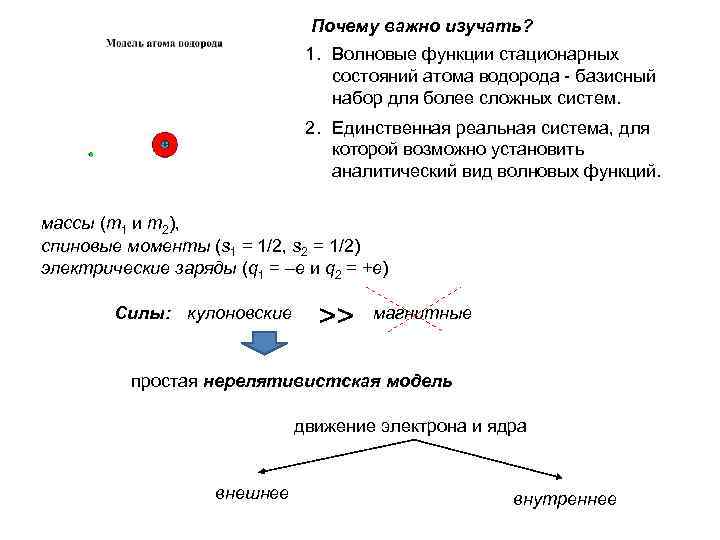 Почему важно изучать? 1. Волновые функции стационарных состояний атома водорода - базисный набор для более сложных систем. 2. Единственная реальная система, для которой возможно установить аналитический вид волновых функций. массы (m 1 и m 2), спиновые моменты (s 1 = 1/2, s 2 = 1/2) электрические заряды (q 1 = –е и q 2 = +е) Силы: кулоновские >> магнитные простая нерелятивистская модель движение электрона и ядра внешнее внутреннее
Почему важно изучать? 1. Волновые функции стационарных состояний атома водорода - базисный набор для более сложных систем. 2. Единственная реальная система, для которой возможно установить аналитический вид волновых функций. массы (m 1 и m 2), спиновые моменты (s 1 = 1/2, s 2 = 1/2) электрические заряды (q 1 = –е и q 2 = +е) Силы: кулоновские >> магнитные простая нерелятивистская модель движение электрона и ядра внешнее внутреннее
 Для начала ограничимся рассмотрением только внешних (пространственных) движений частиц состояния атома водорода удобно представить в пространственном базисе: | = C 1| 1 + C 2| 2 + • • • = Ci| i (x 1, y 1, z 1, x 2, y 2, z 2) i положения обеих частиц в пространстве относительно фиксированной лабораторной системы координат Удобнее — волновая функция Ф(x 1, y 1, z 1, x 2, y 2, z 2; t) = Ф(x 1, y 1, z 1, x 2, y 2, z 2) exp(i t), где = Е/ пространственная часть Найти из НФ = ЕФ энергия
Для начала ограничимся рассмотрением только внешних (пространственных) движений частиц состояния атома водорода удобно представить в пространственном базисе: | = C 1| 1 + C 2| 2 + • • • = Ci| i (x 1, y 1, z 1, x 2, y 2, z 2) i положения обеих частиц в пространстве относительно фиксированной лабораторной системы координат Удобнее — волновая функция Ф(x 1, y 1, z 1, x 2, y 2, z 2; t) = Ф(x 1, y 1, z 1, x 2, y 2, z 2) exp(i t), где = Е/ пространственная часть Найти из НФ = ЕФ энергия
 Оператор Гамильтона двухчастичной системы "набла-квадрат" Уравнение на собственные значения ("стационарное уравнение Шредингера") Решениями этого уравнения являются волновые функции, описывающие все возможные стационарные состояния атома водорода и их энергии
Оператор Гамильтона двухчастичной системы "набла-квадрат" Уравнение на собственные значения ("стационарное уравнение Шредингера") Решениями этого уравнения являются волновые функции, описывающие все возможные стационарные состояния атома водорода и их энергии
 Если атом изолирован от окружающих тел, то движения частиц в нем можно разделить на два невзаимодействующих типа: 1) глобальное движение атома как материальной точки (центра масс) в лабораторной системе координат (X, Y, Z). 2) локальные движения частиц во внутренней системе координат (x, y, z), начало которой расположено в центре масс. Независимость внешнего и внутреннего движений позволяет представить шестимерную волновую функцию в виде произведения двух трехмерных функций: Ф (x 1, y 1, z 1, x 2, y 2, z 2) = Ф' (X, Y, Z) Ф'' (x, y, z) где M = m 1 + m 2 ("свободная частица" или "частица в трехмерном потенциальном ящике")
Если атом изолирован от окружающих тел, то движения частиц в нем можно разделить на два невзаимодействующих типа: 1) глобальное движение атома как материальной точки (центра масс) в лабораторной системе координат (X, Y, Z). 2) локальные движения частиц во внутренней системе координат (x, y, z), начало которой расположено в центре масс. Независимость внешнего и внутреннего движений позволяет представить шестимерную волновую функцию в виде произведения двух трехмерных функций: Ф (x 1, y 1, z 1, x 2, y 2, z 2) = Ф' (X, Y, Z) Ф'' (x, y, z) где M = m 1 + m 2 ("свободная частица" или "частица в трехмерном потенциальном ящике")
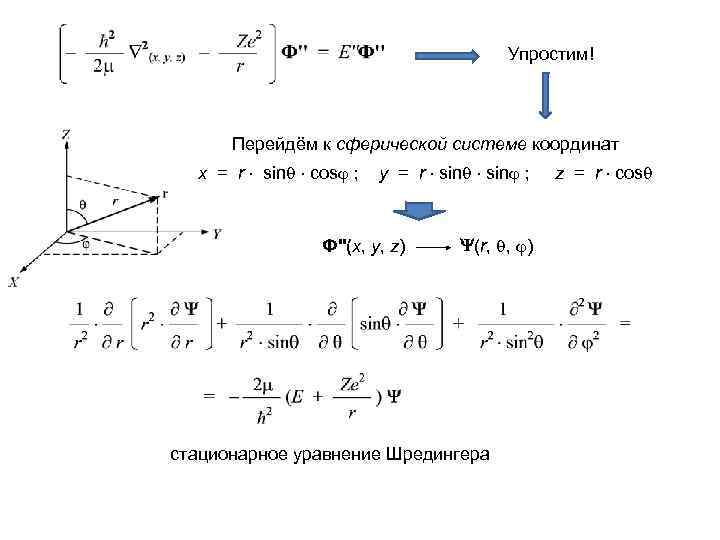 Упростим! Перейдём к сферической системе координат x = r sin cos ; y = r sin ; Ф''(x, y, z) (r, , ) стационарное уравнение Шредингера z = r cos
Упростим! Перейдём к сферической системе координат x = r sin cos ; y = r sin ; Ф''(x, y, z) (r, , ) стационарное уравнение Шредингера z = r cos
 Сделанная замена переменных позволяет представить трехмерную функцию в виде произведения трех одномерных функций-сомножителей: (r, , ) = R(r) ( ) дискретный набор решений при = 0, 1, 4, 9, 16, 25, … и = 0, 2, 6, 12, 20, 30, 42, … Упростим! = l(l + 1) , = m m , где l = 0, 1, 2, . . . где m = 0, 1, 2, . . .
Сделанная замена переменных позволяет представить трехмерную функцию в виде произведения трех одномерных функций-сомножителей: (r, , ) = R(r) ( ) дискретный набор решений при = 0, 1, 4, 9, 16, 25, … и = 0, 2, 6, 12, 20, 30, 42, … Упростим! = l(l + 1) , = m m , где l = 0, 1, 2, . . . где m = 0, 1, 2, . . .
 Дискретность в решениях R-, - и -уравнений, вызываемая приведенными ограничениями для параметров и , приводит, в свою очередь, к дискретности допустимых значений энергии атома, связанной с его внутренним движением: Целые числа, входящие в приведенные формулы, называются квантовыми числами атома водорода: n — главное, l — орбитальное, m — магнитное. n = 1, 2, 3, . . . l = 0, 1, 2, . . . m = 0, 1, 2, . . . Они выступают в роли параметров, нумерующих возможные решения уравнения Шредингера: (r, , ) = R(r) • ( ) = (n, l, m) = R(n, l) • (l, m) • (m) = = R(n, l) • Y(l, m) Произведения (l, m) • (m) = Y(l, m) называются шаровыми функциями.
Дискретность в решениях R-, - и -уравнений, вызываемая приведенными ограничениями для параметров и , приводит, в свою очередь, к дискретности допустимых значений энергии атома, связанной с его внутренним движением: Целые числа, входящие в приведенные формулы, называются квантовыми числами атома водорода: n — главное, l — орбитальное, m — магнитное. n = 1, 2, 3, . . . l = 0, 1, 2, . . . m = 0, 1, 2, . . . Они выступают в роли параметров, нумерующих возможные решения уравнения Шредингера: (r, , ) = R(r) • ( ) = (n, l, m) = R(n, l) • (l, m) • (m) = = R(n, l) • Y(l, m) Произведения (l, m) • (m) = Y(l, m) называются шаровыми функциями.
 Приведем явный вид R- , - и -функций (в сферических координатах). Нормировочный множитель присоединенный полином Лежандра
Приведем явный вид R- , - и -функций (в сферических координатах). Нормировочный множитель присоединенный полином Лежандра
 Для R-уравнения решения имеют вид: присоединенный полином Лаггера Нормировочный множитель = (Z/ao) r новая шкала расстояний ао = 4 oh 2/ e 2 0, 053 нм o = 8, 84 10– 12 ф/м "атомных единиц длины" диэлектрическая постоянная
Для R-уравнения решения имеют вид: присоединенный полином Лаггера Нормировочный множитель = (Z/ao) r новая шкала расстояний ао = 4 oh 2/ e 2 0, 053 нм o = 8, 84 10– 12 ф/м "атомных единиц длины" диэлектрическая постоянная
 Конкретные выражения для волновых функций с небольшими номерами. Rn, l-функции (нормировочные множители опущены): - функции (нормировочные множители опущены): Ф-функции (нормировочные множители опущены):
Конкретные выражения для волновых функций с небольшими номерами. Rn, l-функции (нормировочные множители опущены): - функции (нормировочные множители опущены): Ф-функции (нормировочные множители опущены):
 Располагая таблицами таких функций, можно легко построить явный вид волновой функции для любого стационарного состояния атома водорода. Пусть состояние характеризуется квантовыми числами {n, l, m} = {2, 1, – 1}. Тогда волновая функция будет иметь вид (нормировочный множитель опущен): Полный вид волновой функции получим при умножении этой пространственной части на временной экспоненциальный множитель: (2, 1, – 1), t = (2, 1, – 1) exp[i(E 2/h)t] , где Е 2 — энергия, соответствующая значению n = 2. n, l, m водородные атомные орбитали или Н-АО комплексные атомные орбитали (КАО)
Располагая таблицами таких функций, можно легко построить явный вид волновой функции для любого стационарного состояния атома водорода. Пусть состояние характеризуется квантовыми числами {n, l, m} = {2, 1, – 1}. Тогда волновая функция будет иметь вид (нормировочный множитель опущен): Полный вид волновой функции получим при умножении этой пространственной части на временной экспоненциальный множитель: (2, 1, – 1), t = (2, 1, – 1) exp[i(E 2/h)t] , где Е 2 — энергия, соответствующая значению n = 2. n, l, m водородные атомные орбитали или Н-АО комплексные атомные орбитали (КАО)
 Более удобная номенклатура Значение l Символ 0 1 2 3 4 s p d f g … 5 h … 100 = 1 so 200 = 2 so 210 = 2 po 21– 1 = 2 p– 1 211 = 2 p 1 300 = 3 so 310 = 3 po 31– 1 = 3 p– 1 311 = 3 p 1 320 = 3 do 321 = 3 d 1 32– 1 = 3 d– 1 . . . и т. д. Ещё удобнее пользоваться действительными функциями! Получим линейные комбинации волновых функций: (n, l, m) + (n, l, –m) = R ( e im + e –im ) = R • cos (m ) = +( n, l, |m|) (n, l, m) – (n, l, –m) = R ( e im – e –im ) = R • sin (m ) = –( n, l, |m|) Действительные атомные орбитали (ДАО)
Более удобная номенклатура Значение l Символ 0 1 2 3 4 s p d f g … 5 h … 100 = 1 so 200 = 2 so 210 = 2 po 21– 1 = 2 p– 1 211 = 2 p 1 300 = 3 so 310 = 3 po 31– 1 = 3 p– 1 311 = 3 p 1 320 = 3 do 321 = 3 d 1 32– 1 = 3 d– 1 . . . и т. д. Ещё удобнее пользоваться действительными функциями! Получим линейные комбинации волновых функций: (n, l, m) + (n, l, –m) = R ( e im + e –im ) = R • cos (m ) = +( n, l, |m|) (n, l, m) – (n, l, –m) = R ( e im – e –im ) = R • sin (m ) = –( n, l, |m|) Действительные атомные орбитали (ДАО)
 В обозначениях ДАО нижний индекс заменяется на буквенный. Например: (2 р1 + 2 р– 1) ~ 2 px (2 р1 – 2 р– 1) ~ 2 py (3 d 1 + 3 d– 1) ~ 3 dxz (3 d 1 – 3 d– 1) ~ 3 dyz (3 d 2 + 3 d– 2) ~ 3 d(x 2– y 2) (3 d 2 – 3 d– 2) ~ 3 dxy 2 р0 ~ 2 pz 3 d 0 ~ 3 dz 2 КАО и ДАО полностью эквивалентны в математическом отношении и представляют собой два базисных набора в одном и том же пространстве состояний ДАО удобны в том отношении, что их можно изображать графически, анализировать различные пространственные характеристики и симметрию.
В обозначениях ДАО нижний индекс заменяется на буквенный. Например: (2 р1 + 2 р– 1) ~ 2 px (2 р1 – 2 р– 1) ~ 2 py (3 d 1 + 3 d– 1) ~ 3 dxz (3 d 1 – 3 d– 1) ~ 3 dyz (3 d 2 + 3 d– 2) ~ 3 d(x 2– y 2) (3 d 2 – 3 d– 2) ~ 3 dxy 2 р0 ~ 2 pz 3 d 0 ~ 3 dz 2 КАО и ДАО полностью эквивалентны в математическом отношении и представляют собой два базисных набора в одном и том же пространстве состояний ДАО удобны в том отношении, что их можно изображать графически, анализировать различные пространственные характеристики и симметрию.
 Раздел 2 ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ АТОМА ВОДОРОДА
Раздел 2 ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ АТОМА ВОДОРОДА
 ВОЛНОВАЯ ФУНКЦИЯ Физические характеристики атома водорода динамические пространственные
ВОЛНОВАЯ ФУНКЦИЯ Физические характеристики атома водорода динамические пространственные
 Динамические наблюдаемые А (r, , ) = А (r, , ) квантовомеханический оператор Количество независимых наблюдаемых Числовые значения динамических наблюдаемых (собственные значения ) число механических степеней свободы атома фундаментальный набор для атома водорода включает три наблюдаемых: энергия — Е, величина (модуль) вектора орбитального момента — | L |, проекция вектора орбитального момента на ось z — Lz.
Динамические наблюдаемые А (r, , ) = А (r, , ) квантовомеханический оператор Количество независимых наблюдаемых Числовые значения динамических наблюдаемых (собственные значения ) число механических степеней свободы атома фундаментальный набор для атома водорода включает три наблюдаемых: энергия — Е, величина (модуль) вектора орбитального момента — | L |, проекция вектора орбитального момента на ось z — Lz.
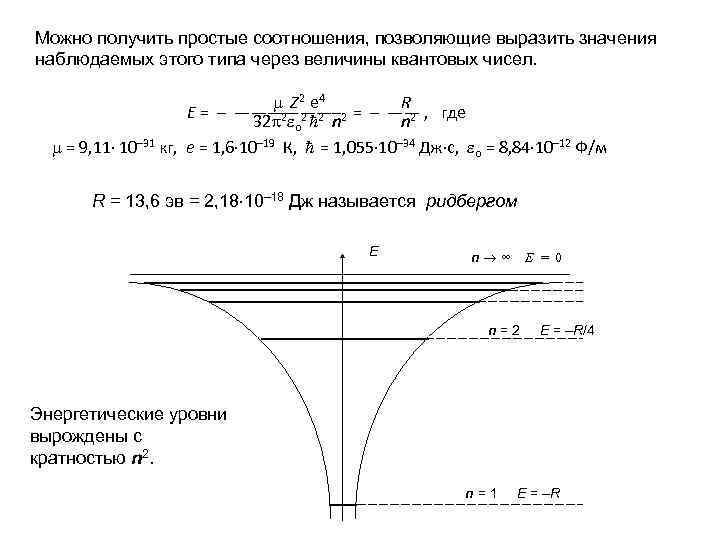 Можно получить простые соотношения, позволяющие выразить значения наблюдаемых этого типа через величины квантовых чисел. Z 2 e 4 R Е = – ——————– 2 = – —— , где 32 2 о 2 2 n n 2 = 9, 11 10– 31 кг, е = 1, 6 10– 19 К, = 1, 055 10– 34 Дж с, о = 8, 84 10– 12 Ф/м R = 13, 6 эв = 2, 18 10– 18 Дж называется ридбергом E n ∞ E = 0 n=2 E = –R/4 Энергетические уровни вырождены с кратностью n 2. n=1 E = –R
Можно получить простые соотношения, позволяющие выразить значения наблюдаемых этого типа через величины квантовых чисел. Z 2 e 4 R Е = – ——————– 2 = – —— , где 32 2 о 2 2 n n 2 = 9, 11 10– 31 кг, е = 1, 6 10– 19 К, = 1, 055 10– 34 Дж с, о = 8, 84 10– 12 Ф/м R = 13, 6 эв = 2, 18 10– 18 Дж называется ридбергом E n ∞ E = 0 n=2 E = –R/4 Энергетические уровни вырождены с кратностью n 2. n=1 E = –R
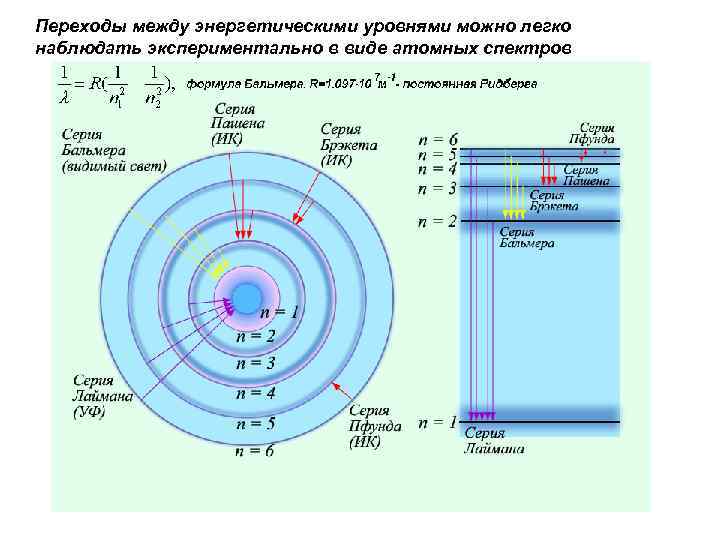 Переходы между энергетическими уровнями можно легко наблюдать экспериментально в виде атомных спектров
Переходы между энергетическими уровнями можно легко наблюдать экспериментально в виде атомных спектров
 Модуль вектора орбитального момента может быть вычислен по формуле: | L | = l(l+1) = 0, 2 , 6 , 12 и т. д. для каждого энергетического уровня вектор L может иметь только (n – 1) значение модуля | L | Модуль вектора L связан с пространственным распределением плотности электронного облака и числом узловых поверхностей, разделяющим облако на отдельные фрагменты. Величина проекции вектора L на ось z, характеризующая пространственную ориентацию этого вектора, задается магнитным квантовым числом: Lz = m = 0, , 2 , 3 . . . l
Модуль вектора орбитального момента может быть вычислен по формуле: | L | = l(l+1) = 0, 2 , 6 , 12 и т. д. для каждого энергетического уровня вектор L может иметь только (n – 1) значение модуля | L | Модуль вектора L связан с пространственным распределением плотности электронного облака и числом узловых поверхностей, разделяющим облако на отдельные фрагменты. Величина проекции вектора L на ось z, характеризующая пространственную ориентацию этого вектора, задается магнитным квантовым числом: Lz = m = 0, , 2 , 3 . . . l
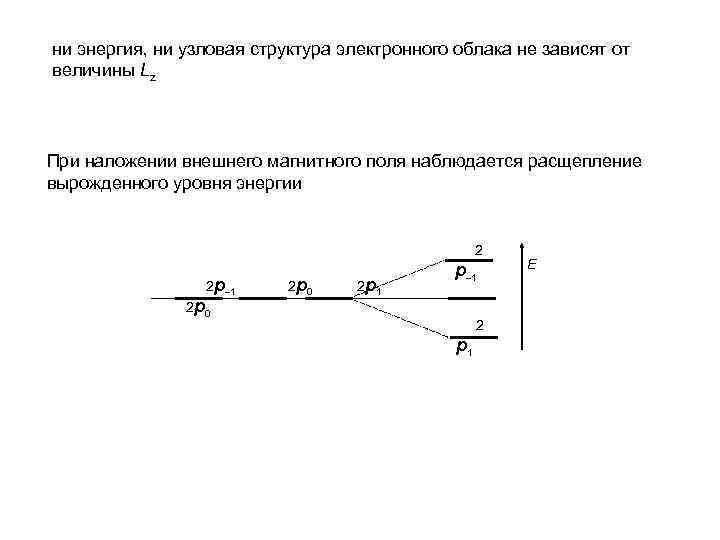 ни энергия, ни узловая структура электронного облака не зависят от величины Lz При наложении внешнего магнитного поля наблюдается расщепление вырожденного уровня энергии 2 2 р– 1 2 р 0 2 р 1 р– 1 2 р1 Е
ни энергия, ни узловая структура электронного облака не зависят от величины Lz При наложении внешнего магнитного поля наблюдается расщепление вырожденного уровня энергии 2 2 р– 1 2 р 0 2 р 1 р– 1 2 р1 Е
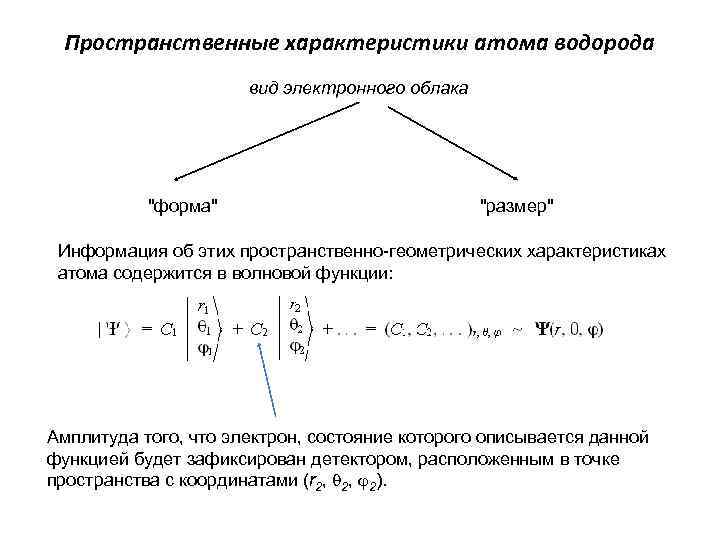 Пространственные характеристики атома водорода вид электронного облака "форма" "размер" Информация об этих пространственно-геометрических характеристиках атома содержится в волновой функции: Амплитуда того, что электрон, состояние которого описывается данной функцией будет зафиксирован детектором, расположенным в точке пространства с координатами (r 2, 2).
Пространственные характеристики атома водорода вид электронного облака "форма" "размер" Информация об этих пространственно-геометрических характеристиках атома содержится в волновой функции: Амплитуда того, что электрон, состояние которого описывается данной функцией будет зафиксирован детектором, расположенным в точке пространства с координатами (r 2, 2).
 Пространственную зависимость плотности электронного облака описывает квадрат волновой функции: P(r, , ) = | (r, , )|2 Для стационарного состояния характеристики электронного облака будут постоянны во времени. плотность электронного облака Радиальная зависимость Угловая зависимость
Пространственную зависимость плотности электронного облака описывает квадрат волновой функции: P(r, , ) = | (r, , )|2 Для стационарного состояния характеристики электронного облака будут постоянны во времени. плотность электронного облака Радиальная зависимость Угловая зависимость
 Радиальная зависимость показывает характер изменения плотности электронного облака при перемещении вдоль радиуса r при постоянных значениях углов и . Радиальная зависимость через радиальный множитель R(r) "функция радиального распределения" (ФРР) В общем случае, радиальные части волновых функций для различных стационарных состояний атома водорода можно охарактеризовать числом узлов, которое определяется формулой: Nрад = n – l – 1.
Радиальная зависимость показывает характер изменения плотности электронного облака при перемещении вдоль радиуса r при постоянных значениях углов и . Радиальная зависимость через радиальный множитель R(r) "функция радиального распределения" (ФРР) В общем случае, радиальные части волновых функций для различных стационарных состояний атома водорода можно охарактеризовать числом узлов, которое определяется формулой: Nрад = n – l – 1.
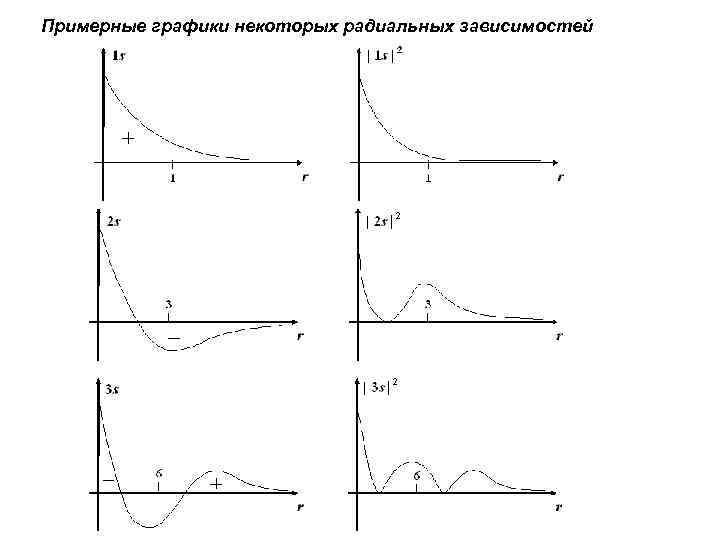 Примерные графики некоторых радиальных зависимостей
Примерные графики некоторых радиальных зависимостей
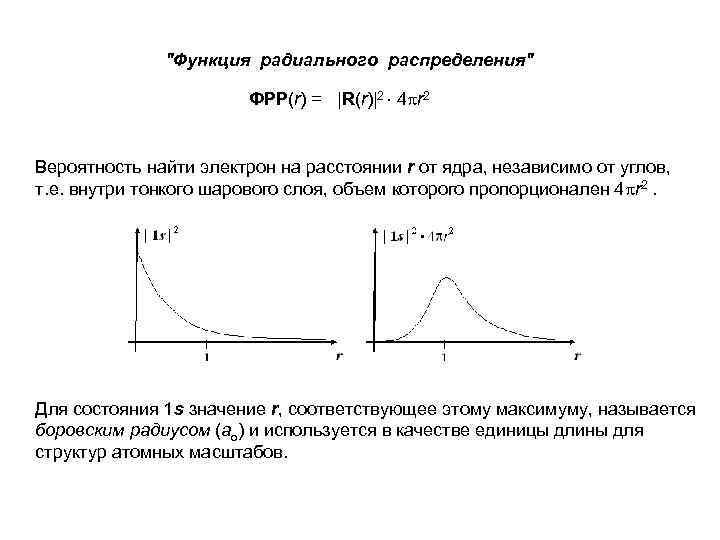 "Функция радиального распределения" ФРР(r) = |R(r)|2 4 r 2 Вероятность найти электрон на расстоянии r от ядра, независимо от углов, т. е. внутри тонкого шарового слоя, объем которого пропорционален 4 r 2. Для состояния 1 s значение r, соответствующее этому максимуму, называется боровским радиусом (ао) и используется в качестве единицы длины для структур атомных масштабов.
"Функция радиального распределения" ФРР(r) = |R(r)|2 4 r 2 Вероятность найти электрон на расстоянии r от ядра, независимо от углов, т. е. внутри тонкого шарового слоя, объем которого пропорционален 4 r 2. Для состояния 1 s значение r, соответствующее этому максимуму, называется боровским радиусом (ао) и используется в качестве единицы длины для структур атомных масштабов.
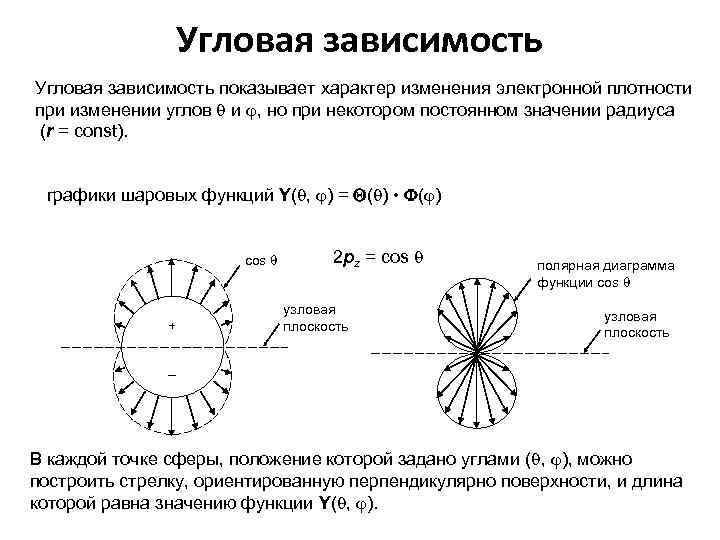 Угловая зависимость показывает характер изменения электронной плотности при изменении углов и , но при некотором постоянном значении радиуса (r = const). графики шаровых функций Y( , ) = ( ) • ( ) cos + 2 рz = cos узловая плоскость полярная диаграмма функции cos узловая плоскость – В каждой точке сферы, положение которой задано углами ( , ), можно построить стрелку, ориентированную перпендикулярно поверхности, и длина которой равна значению функции Y( , ).
Угловая зависимость показывает характер изменения электронной плотности при изменении углов и , но при некотором постоянном значении радиуса (r = const). графики шаровых функций Y( , ) = ( ) • ( ) cos + 2 рz = cos узловая плоскость полярная диаграмма функции cos узловая плоскость – В каждой точке сферы, положение которой задано углами ( , ), можно построить стрелку, ориентированную перпендикулярно поверхности, и длина которой равна значению функции Y( , ).
 В ряде случаев можно ограничиться указанием только узловой структуры функции, не обращая внимания на длины стрелок. узловые поверхности + + s-АО – + – p-АО d-АО Из рисунка видно, что число узловых поверхностей углового типа растет пропорционально орбитальному квантовому числу: Nугл = l.
В ряде случаев можно ограничиться указанием только узловой структуры функции, не обращая внимания на длины стрелок. узловые поверхности + + s-АО – + – p-АО d-АО Из рисунка видно, что число узловых поверхностей углового типа растет пропорционально орбитальному квантовому числу: Nугл = l.
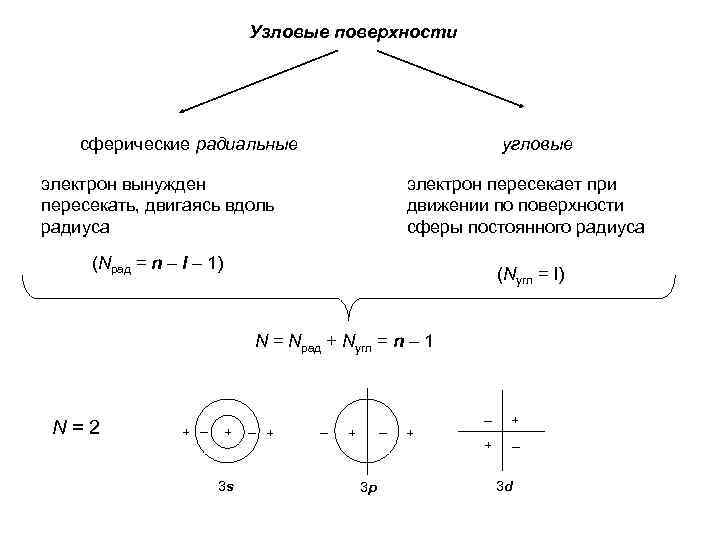 Узловые поверхности сферические радиальные угловые электрон вынужден пересекать, двигаясь вдоль радиуса электрон пересекает при движении по поверхности сферы постоянного радиуса (Nрад = n – l – 1) (Nугл = l) N = Nрад + Nугл = n – 1 N=2 + – + 3 s – + – – + 3 p + – + + – 3 d
Узловые поверхности сферические радиальные угловые электрон вынужден пересекать, двигаясь вдоль радиуса электрон пересекает при движении по поверхности сферы постоянного радиуса (Nрад = n – l – 1) (Nугл = l) N = Nрад + Nугл = n – 1 N=2 + – + 3 s – + – – + 3 p + – + + – 3 d
 Еще один способ описания пространственных характеристик электронного облака заключается в построении т. н. "изовероятных поверхностей" (ИВП). Каждая ИВП представляет собой график функции | (r, , )|2 = const независимо от углов и радиуса при const = 0 узловые поверхности Вместо совокупности ИВП часто используют только одну из них — такую, внутри которой заключена определенная доля (например, 90 или 95 %) всей электронной плотности облака.
Еще один способ описания пространственных характеристик электронного облака заключается в построении т. н. "изовероятных поверхностей" (ИВП). Каждая ИВП представляет собой график функции | (r, , )|2 = const независимо от углов и радиуса при const = 0 узловые поверхности Вместо совокупности ИВП часто используют только одну из них — такую, внутри которой заключена определенная доля (например, 90 или 95 %) всей электронной плотности облака.
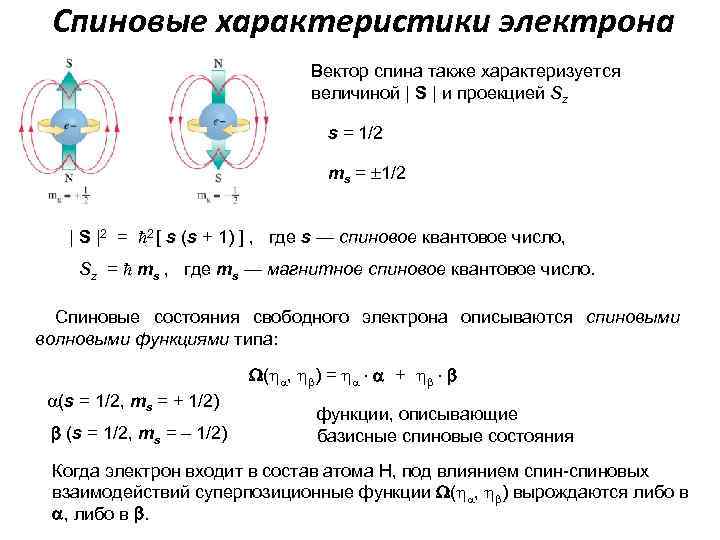 Спиновые характеристики электрона Вектор спина также характеризуется величиной | S | и проекцией Sz s = 1/2 ms = 1/2 | S |2 = 2 [ s (s + 1) ] , где s — спиновое квантовое число, Sz = ms , где ms — магнитное спиновое квантовое число. Спиновые состояния свободного электрона описываются спиновыми волновыми функциями типа: (s = 1/2, ms = + 1/2) (s = 1/2, ms = – 1/2) ( , ) = + функции, описывающие базисные спиновые состояния Когда электрон входит в состав атома Н, под влиянием спин-спиновых взаимодействий суперпозиционные функции ( , ) вырождаются либо в , либо в .
Спиновые характеристики электрона Вектор спина также характеризуется величиной | S | и проекцией Sz s = 1/2 ms = 1/2 | S |2 = 2 [ s (s + 1) ] , где s — спиновое квантовое число, Sz = ms , где ms — магнитное спиновое квантовое число. Спиновые состояния свободного электрона описываются спиновыми волновыми функциями типа: (s = 1/2, ms = + 1/2) (s = 1/2, ms = – 1/2) ( , ) = + функции, описывающие базисные спиновые состояния Когда электрон входит в состав атома Н, под влиянием спин-спиновых взаимодействий суперпозиционные функции ( , ) вырождаются либо в , либо в .
 В нерелятивистском приближении: Полная волновая функция (r, , , ) = (r, , ) • ( ) атомные спин-орбитали (АСО) = 1/2 АСО определяется набором из пяти квантовых чисел { n, l, ml, s, ms } {n, l, ms} Такой набор полностью определяет как волновую функцию, так и четыре наблюдаемые, составляющие фундаментальный набор: энергию, длину и проекцию вектора орбитального момента, проекцию вектора спина: { E |L| Lz Sz } ~ {n l ml ms }
В нерелятивистском приближении: Полная волновая функция (r, , , ) = (r, , ) • ( ) атомные спин-орбитали (АСО) = 1/2 АСО определяется набором из пяти квантовых чисел { n, l, ml, s, ms } {n, l, ms} Такой набор полностью определяет как волновую функцию, так и четыре наблюдаемые, составляющие фундаментальный набор: энергию, длину и проекцию вектора орбитального момента, проекцию вектора спина: { E |L| Lz Sz } ~ {n l ml ms }
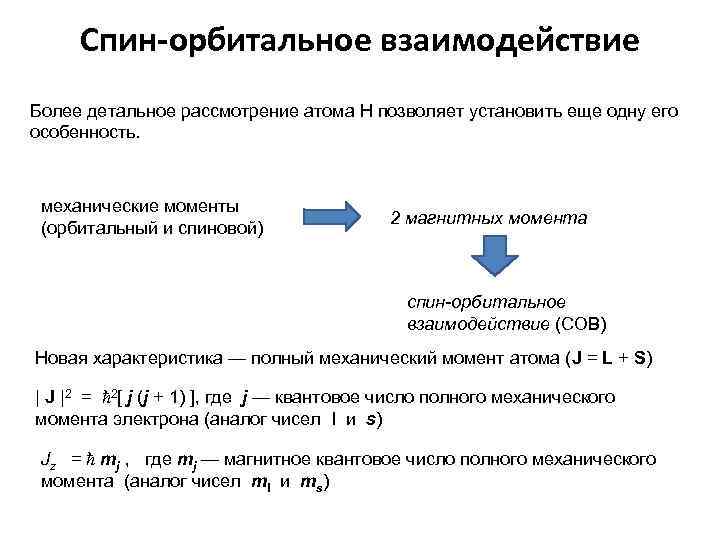 Спин-орбитальное взаимодействие Более детальное рассмотрение атома Н позволяет установить еще одну его особенность. механические моменты (орбитальный и спиновой) 2 магнитных момента спин-орбитальное взаимодействие (СОВ) Новая характеристика — полный механический момент атома (J = L + S) | J |2 = 2[ j (j + 1) ], где j — квантовое число полного механического момента электрона (аналог чисел l и s) Jz = mj , где mj — магнитное квантовое число полного механического момента (аналог чисел ml и ms)
Спин-орбитальное взаимодействие Более детальное рассмотрение атома Н позволяет установить еще одну его особенность. механические моменты (орбитальный и спиновой) 2 магнитных момента спин-орбитальное взаимодействие (СОВ) Новая характеристика — полный механический момент атома (J = L + S) | J |2 = 2[ j (j + 1) ], где j — квантовое число полного механического момента электрона (аналог чисел l и s) Jz = mj , где mj — магнитное квантовое число полного механического момента (аналог чисел ml и ms)
 Квантовое число j может быть рассчитано по такому правилу: максимальное значение числа j равно сумме чисел (l + s) минимальное — равно модулю разности между ними | l – s | Остальные значения располагаются между этими двумя крайними значениями с шагом 1 Для каждого значения числа j имеется (2 j + 1) значение числа mj = j, (j – 1), . . , (–j + 1), –j.
Квантовое число j может быть рассчитано по такому правилу: максимальное значение числа j равно сумме чисел (l + s) минимальное — равно модулю разности между ними | l – s | Остальные значения располагаются между этими двумя крайними значениями с шагом 1 Для каждого значения числа j имеется (2 j + 1) значение числа mj = j, (j – 1), . . , (–j + 1), –j.
 Например, пусть имеется электрон в состоянии 3 d. l = 2 и s = 1/2 число j может иметь всего два допустимых значения: j = 2 + 1/2 = 5/2 и j = 2 – 1/2 = 3/2. сложение векторов L и S может привести только к двум результирующим векторам J: | J | = [ 5/2 (5/2 + 1)]1/2 = (35)1/2/2 Вектор такой длины может иметь 2(5/2) + 1 = 6 проекций mj = 5/2, 3/2, 1/2, – 3/2, – 5/2 | J | = [ 3/2 (3/2 + 1)]1/2 = (15)1/2/2 Вектор такой длины может иметь 2(3/2) + 1 = 4 проекции mj = 3/2, 1/2, – 3/2
Например, пусть имеется электрон в состоянии 3 d. l = 2 и s = 1/2 число j может иметь всего два допустимых значения: j = 2 + 1/2 = 5/2 и j = 2 – 1/2 = 3/2. сложение векторов L и S может привести только к двум результирующим векторам J: | J | = [ 5/2 (5/2 + 1)]1/2 = (35)1/2/2 Вектор такой длины может иметь 2(5/2) + 1 = 6 проекций mj = 5/2, 3/2, 1/2, – 3/2, – 5/2 | J | = [ 3/2 (3/2 + 1)]1/2 = (15)1/2/2 Вектор такой длины может иметь 2(3/2) + 1 = 4 проекции mj = 3/2, 1/2, – 3/2
 Таким образом, набор пяти наблюдаемых (и нумерующих их квантовых чисел), определяющих стационарное состояние электрона, при учете СОВ заменяется другим набором:
Таким образом, набор пяти наблюдаемых (и нумерующих их квантовых чисел), определяющих стационарное состояние электрона, при учете СОВ заменяется другим набором:
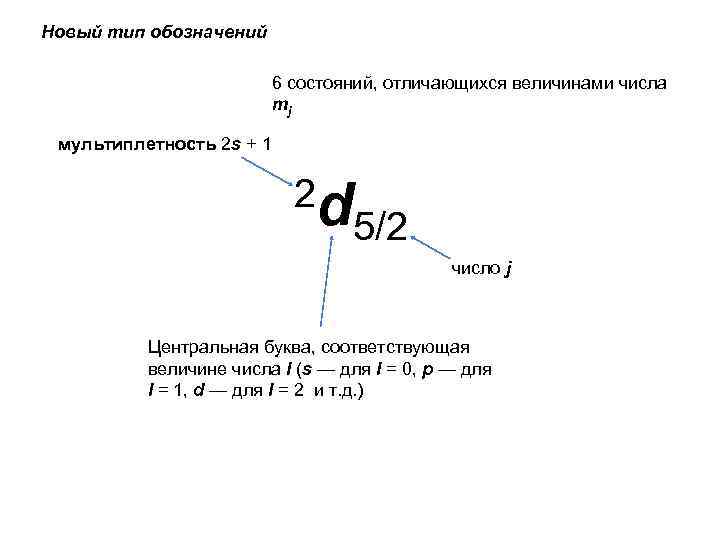 Новый тип обозначений 6 состояний, отличающихся величинами числа mj мультиплетность 2 s + 1 2 d 5/2 число j Центральная буква, соответствующая величине числа l (s — для l = 0, р — для l = 1, d — для l = 2 и т. д. )
Новый тип обозначений 6 состояний, отличающихся величинами числа mj мультиплетность 2 s + 1 2 d 5/2 число j Центральная буква, соответствующая величине числа l (s — для l = 0, р — для l = 1, d — для l = 2 и т. д. )
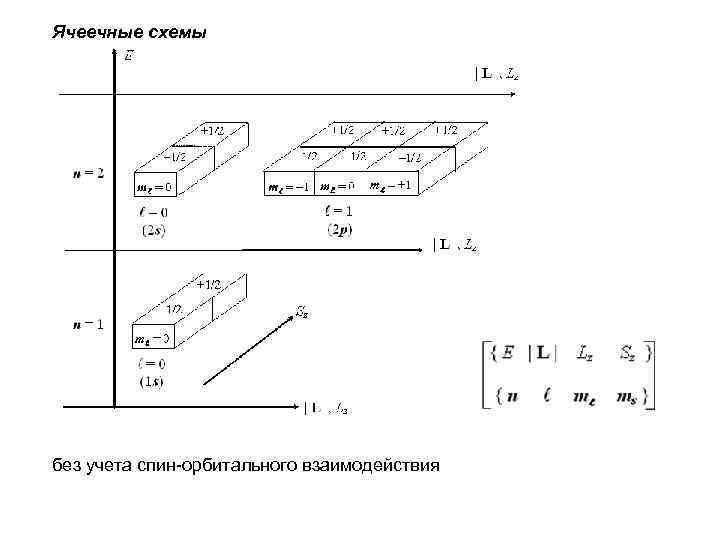 Ячеечные схемы без учета спин-орбитального взаимодействия
Ячеечные схемы без учета спин-орбитального взаимодействия
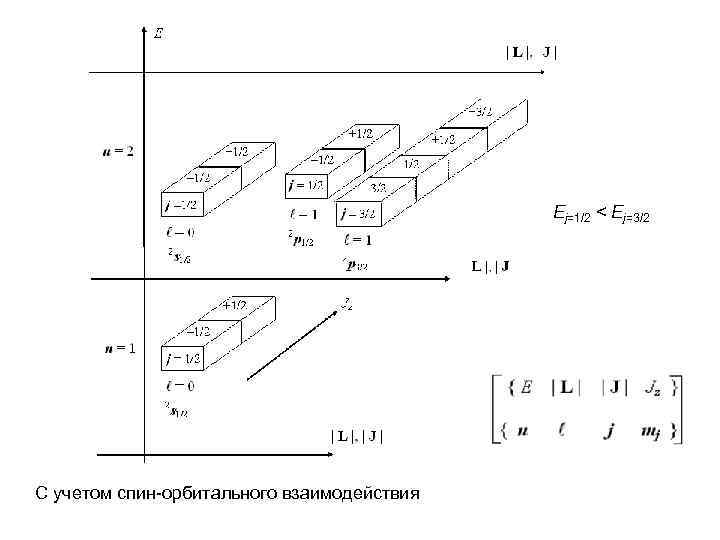 Ej=1/2 < Ej=3/2 С учетом спин-орбитального взаимодействия
Ej=1/2 < Ej=3/2 С учетом спин-орбитального взаимодействия
 Энергетическая диаграмма атома водорода порядка 10– 5 э. В
Энергетическая диаграмма атома водорода порядка 10– 5 э. В
 С некоторыми оговорками (в рамках т. н. "одноэлектронного приближения") обе эти схемы могут применяться для описания многоэлектронных атомов. Электроны распределяются по ячейкам-состояниям, в соответствии с определенными правилами (типа правил Клечковского, принципа Паули и т. д. ).
С некоторыми оговорками (в рамках т. н. "одноэлектронного приближения") обе эти схемы могут применяться для описания многоэлектронных атомов. Электроны распределяются по ячейкам-состояниям, в соответствии с определенными правилами (типа правил Клечковского, принципа Паули и т. д. ).


