Атом водорода Описание атома водорода играет в квантовой

Атом водорода Описание атома водорода играет в квантовой химии фундаментальную роль 1) атом водорода — это единственная реальная система, для которой возможно установить точный аналитический вид волновых функций 2) волновые функции стационарных состояний атома водорода образуют базисный набор, который можно использовать для анализа волновых функций более сложных систем — многоэлектронных атомов и молекул Водородоподобные атомы (ядро + 1 электрон) He+ Li 2+ Be 3+ …

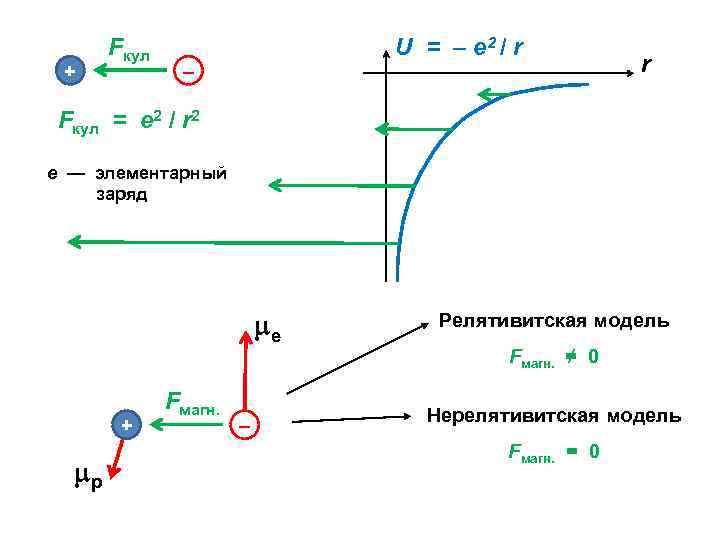+ Fкул U = – e 2 / r – r Fкул = e 2 / r 2 е — элементарный заряд е + р Fмагн. – Релятивитская модель Fмагн. ≠ 0 Нерелятивитская модель Fмагн. = 0

Задача: найти все стационарные состояния и описать их векторами состояния (волновыми функциями): | Ψ 1 | Ψ 2 … Разложение вектора по базису: | Ψ = С 1 | 1 + С 2 | 2 + … Точки в 6 -мерном конфигурационном пространстве | i = | x 1, y 1, z 1, x 2, y 2, z 2 i Координатное представление

Вектор состояния | Ψ = С 1 | 1 + С 2 | 2 + … Волновая функция Ф(x 1, y 1, z 1, x 2, y 2, z 2; t) = = Ф(x 1, y 1, z 1, x 2, y 2, z 2) exp(iωt), где ω = Е/ Н Ф = ЕФ

Н = Т 1 + Т 2 + U 12 , Т 1 = – ( 2/2 m 1) 2(x 1, y 1, z 1) Т 2 = – ( 2/2 m 2) 2(x 2, y 2, z 2) U 12 = – (Ze 2)/r 2 2 = = —– + —– x 2 y 2 z 2 «набла в квадрате» оператор Лапласа

2 2 Ze 2 – —— (1) – —— (2) – —— Ф = ЕФ 2 m 1 2 m 2 r 1) ГЛОБАЛЬНОЕ движение атома как материальной точки (центра масс) в лабораторной системе координат (X, Y, Z). 2) ЛОКАЛЬНЫЕ движения частиц во внутренней системе координат (x, y, z), начало которой расположено в центре масс. Ф (x 1, y 1, z 1, x 2, y 2, z 2) = = Ф' (X, Y, Z) • Ф'' (x, y, z)

Внешнее уравнение 2 2 – —— X, Y, Z Ф' = ЕФ' 2 M Частица с массой M = m 1 + m 2 в трехмерном потенциальном ящике ny 2 2 2 nx 2 nz 2 Е = EX + EY + EZ = —— —– + —– Ly 2 2 m Lx 2 Lz 2 Ф'(X, Y, Z) = (X) (Y) (Z) = = nx ny nz 8 sin —— x sin —— y sin —— z — V Lx Ly Lz

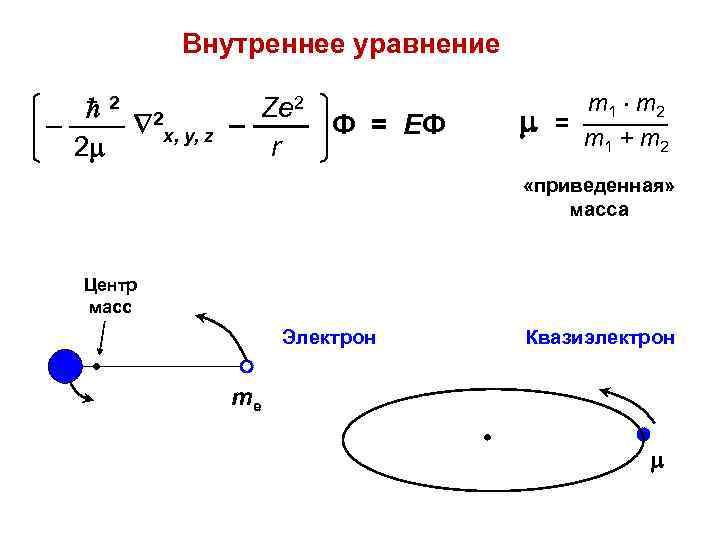Внутреннее уравнение 2 2 Ze 2 – —— x, y, z – —— Ф = ЕФ 2 r m 1 m 2 = ———– m 1 + m 2 «приведенная» масса Центр масс Электрон Квазиэлектрон me

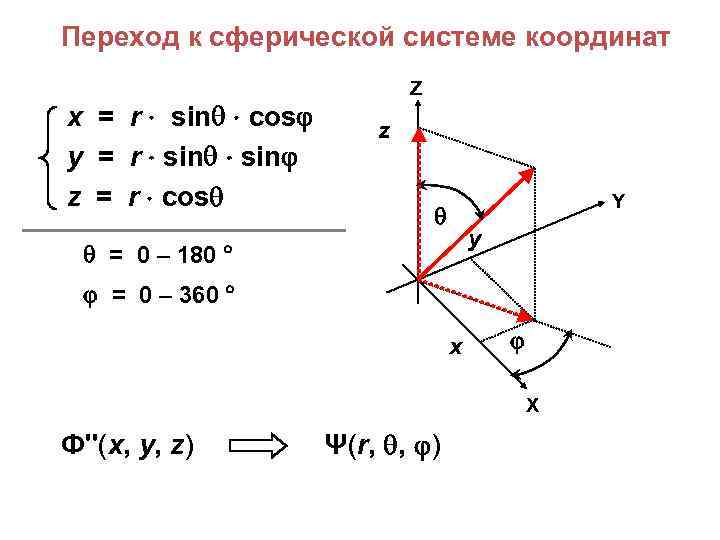Переход к сферической системе координат x = r sin cos y = r sin z = r cos Z z Y y = 0 – 180 = 0 – 360 x X Ф''(x, y, z) Ψ(r, , )

Ψ(r, θ, Φ) = d 2Φ —— + α Φ = 0 dφ2 1 d —— —– sinθ dθ = R(r) Θ(θ) Φ(φ) dΘ α Θ sin —– – ——— + β Θ = 0 dθ sin 2θ Ze 2 β 2 d. R 2μ 1 d – — — r 2 —– – — R + —– E + —— R = 0 r r 2 2 dr r 2 dr

Условие разрешимости системы = 0, 1, 4, 9, 16, 25, 36, … = 0, 2, 6, 12, 20, 30, 42, … Вспомогательные соотношения = m m, где m = 0, 1, 2, . . . = ( + 1), где = 0, 1, 2, . . . m — магнитное квантовое число — орбитальное квантовое число n — главное квантовое число (номер решения)

Ψ(r, , ) = R(r) • Θ( ) • Φ( ) Ψ(n, , m) = R(n, ) • Θ( , m) • Φ(m) Ψ(r, , ) = R(r) • Y( , ) Ψ(n, , m) = R(n, ) • Y( , m) «шаровые» функции Ф-функции Фm = 1 im e 2 { m = 0, 1, 2, … }

Θ-функции Θ |m| = { ≥ |m|} |m| 2 + 1 ( – | m |)! ————— P (cos θ) ( + | m |)! 2 Нормировочный множитель Присоединенный полином Лежандра степени и порядка |m| Θ 0, 0 = 1 Θ 2, 0 = (3 cos 2 θ – 1) Θ 1, 0 = cos θ Θ 2, |1| = sin θ cos θ Θ 1, |1| = sin θ Θ 2, |2| = sin 2 θ

R-функции {n > } 3 Rn = 2 + 1 2ρ 2 Z (n – – 1)! –ρ/n —– ————– e — L (2ρ/n) n nao 2 n[(n + )!]3 n+ Нормировочный множитель ρ = (Z/ao) r R 10 = e R 21 = e –ρ/2 ао = 4 o 2/ e 2 0, 053 нм –ρ/3 –ρ –ρ/2 Присоединенный полином Лаггера R 30 = e (2 – ρ) ρ (27 – 18ρ + 2ρ2) –ρ/3 R 31 = e –ρ/3 R 32 = e (6ρ – ρ2) ρ2

{ ≥ |m|} Полный набор стационарных состояний n = 1 = 0 m = 0 n = 2 = 0 m = 0 = 1 m = – 1 = 2 {n > } n = 3 0 +1 m = – 2 – 1 0 +1 +2

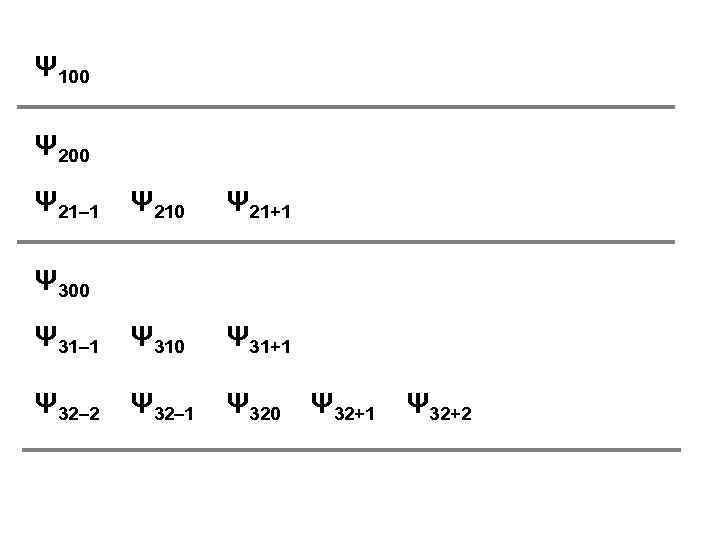Ψ 100 Ψ 21– 1 Ψ 210 Ψ 21+1 Ψ 31– 1 Ψ 310 Ψ 31+1 Ψ 32– 2 Ψ 32– 1 Ψ 320 Ψ 300 Ψ 32+1 Ψ 32+2

n Номенклатура Значение Символ m 0 1 2 3 4 5 … s p d f g h … Ψ 100 = 1 so Ψ 200 = 2 so Ψ 210 = 2 po Ψ 21– 1 = 2 p– 1 Ψ 211 = 2 p 1 Ψ 300 = 3 so Ψ 310 = 3 po Ψ 31– 1 = 3 p– 1 Ψ 311 = 3 p 1 Ψ 320 = 3 do Ψ 32– 1 = 3 d– 1 Ψ 321 = 3 d 1 Ψ 322 = 3 d 2 Ψ 32– 2 = 3 d– 2

Суперпозиционные состояния Ψn = C–m Ψn , –m + … + C+m Ψn , +m Квантовые числа n и определяют пространство состояний { Ψn } с размерностью 2 + 1 Все состояния в таком пространстве характеризуются одним и тем же значением энергии и момента импульса: E = const | L | = const При этом, однако ориентация вектора момента может быть любой: Lz = ? ? ? В пустом пространстве все направления равноправны

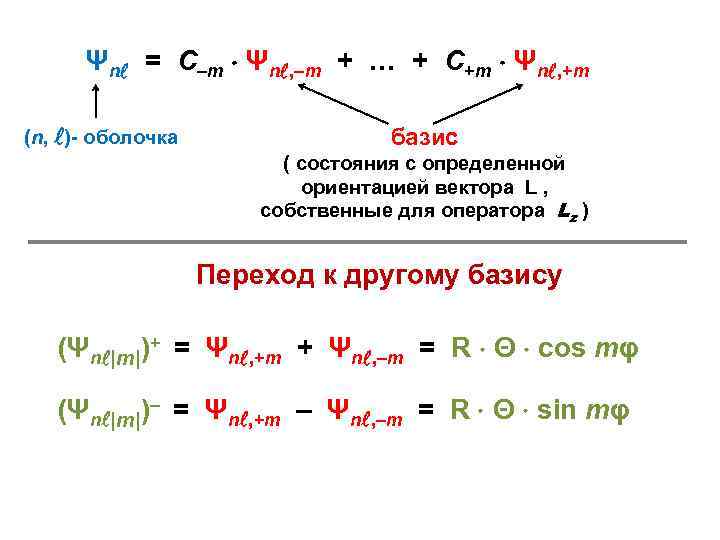Ψn = C–m Ψn , –m + … + C+m Ψn , +m (n, )- оболочка базис ( состояния с определенной ориентацией вектора L , собственные для оператора Lz ) Переход к другому базису (Ψn |m|)+ = Ψn , +m + Ψn , –m = R Θ cos mφ (Ψn |m|)– = Ψn , +m – Ψn , –m = R Θ sin mφ

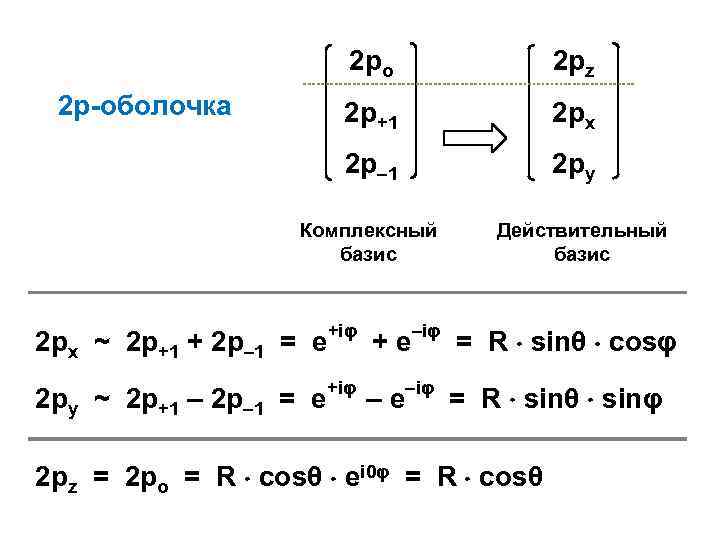2 ро 2 р+1 2 рx 2 р– 1 2 p-оболочка 2 рz 2 рy Комплексный базис Действительный базис 2 рx ~ 2 p+1 + 2 p– 1 = e+iφ + e–iφ = R sinθ cosφ 2 рy ~ 2 p+1 – 2 p– 1 = e+iφ – e–iφ = R sinθ sinφ 2 рz = 2 po = R cosθ ei 0φ = R cosθ

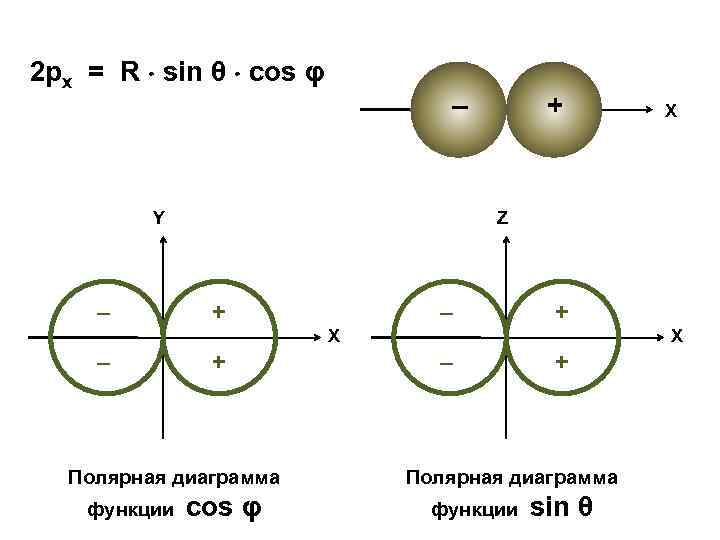2 рx = R sin θ cos φ – Y – + Z + – + X – + Полярная диаграмма функции X cos φ X – + Полярная диаграмма функции sin θ

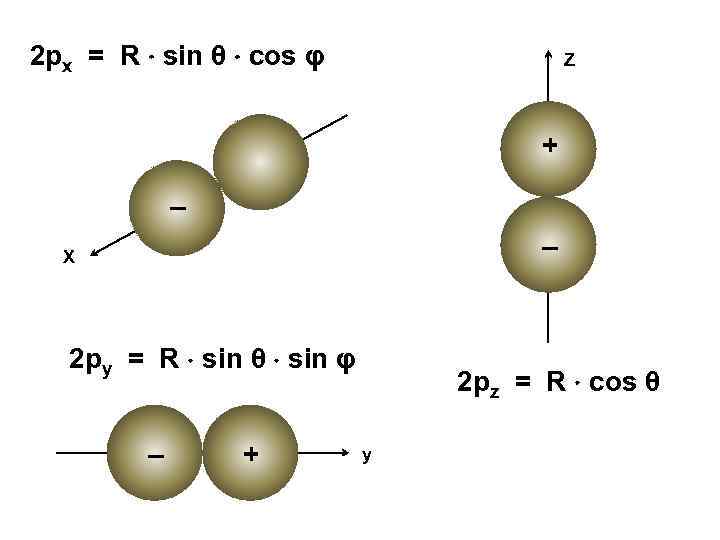2 рx = R sin θ cos φ Z + + – – X 2 рy = R sin θ sin φ – + 2 рz = R cos θ y

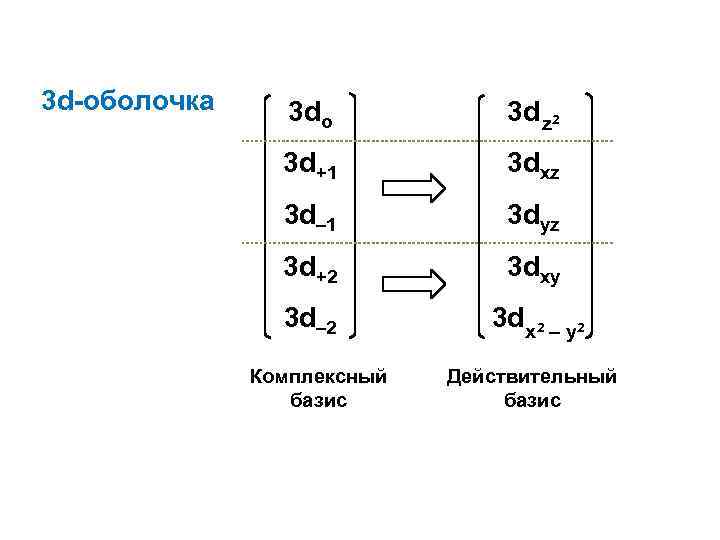3 d-оболочка 3 dо 3 d z 2 3 d+1 3 dxz 3 d– 1 3 dyz 3 d+2 3 dxy 3 d– 2 3 d x 2 – y 2 Комплексный базис Действительный базис

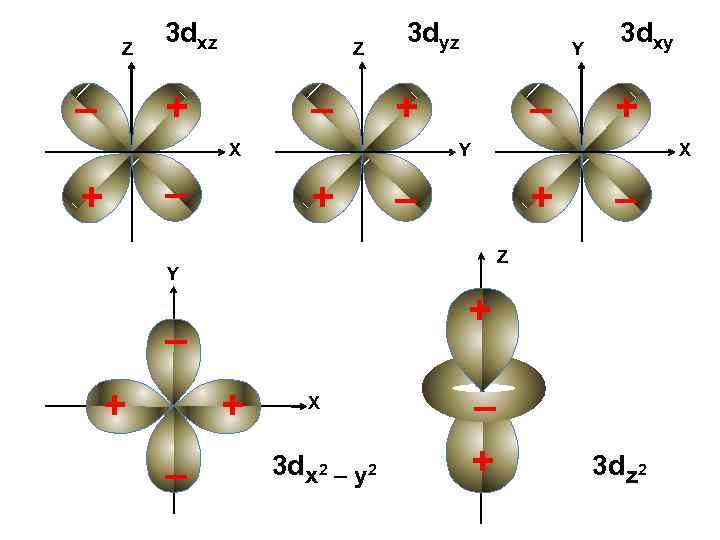Z – 3 dxz Z + – 3 dyz + X + – Y – + X – + – Z + – + Y Y + 3 dxy X 3 d x 2 – y 2 – + 3 d z 2

Нестационарные суперпозиционные состояния Различные значения орбитального квантового числа ( ≠ const ) Ψn = С 1(2 s) + С 2(2 р+1) Различные значения главного квантового числа ( n ≠ const ) Ψ = С 1(1 s) + С 2(2 р+1) Нестационарные состояния быстро релаксируют к одному из стационарных ( ≈ 10– 8 с)

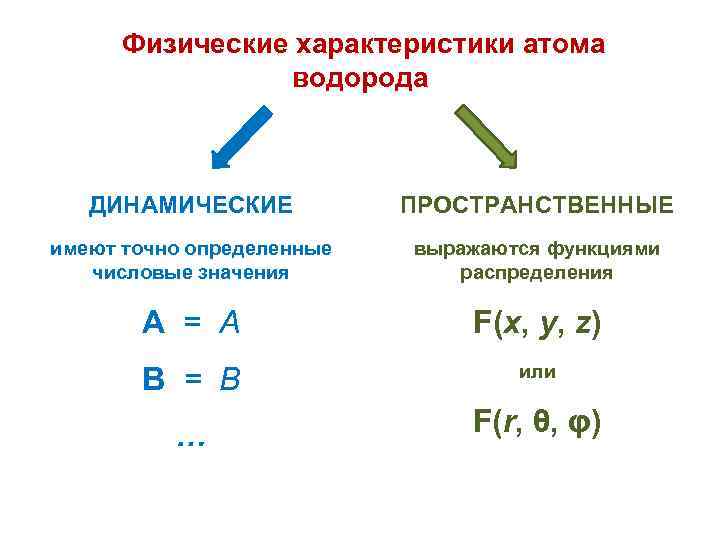Физические характеристики атома водорода ДИНАМИЧЕСКИЕ ПРОСТРАНСТВЕННЫЕ имеют точно определенные числовые значения выражаются функциями распределения А = А F(x, y, z) В = В или … F(r, θ, φ)

Динамические наблюдаемые А Ψ(r, θ, φ) = А Ψ(r, θ, φ) Волновые функции стационарных состояний являются собственными для операторов динамических наблюдаемых HΨ = E Ψ L 2 Ψ = | L | 2 Ψ L z Ψ = Lz Ψ ( E — энергия ) ( | L | — модуль вектора орбитального момента ) ( Lz — проекция вектора орбитального момента )

Энергия (полная) E = T + U Z 2 e 4 R Еn = – ——————– = – —— 32 2 о 2 2 n 2 R — ридберг (единица энергии) = е = 1, 6 10– 19 Кл = 1, 055 10– 34 Дж с R = 13, 6 эв = 2, 18 10– 18 = 9, 11 10– 31 кг Дж о = 8, 84 10– 12 Ф/м Нуль на шкале энергии соответствует бесконечно большому расстоянию между ядром и электроном, поэтому энергии всех связанных состояний отрицательны

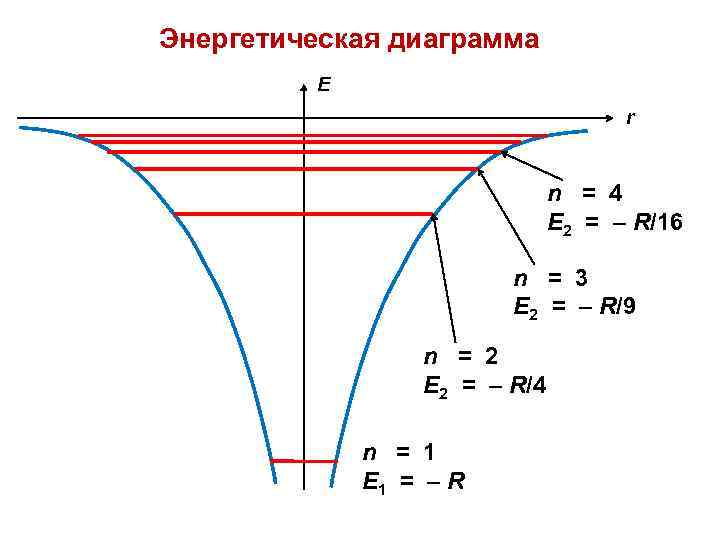Энергетическая диаграмма Е r n = 4 E 2 = – R/16 n = 3 E 2 = – R/9 n = 2 E 2 = – R/4 n = 1 E 1 = – R

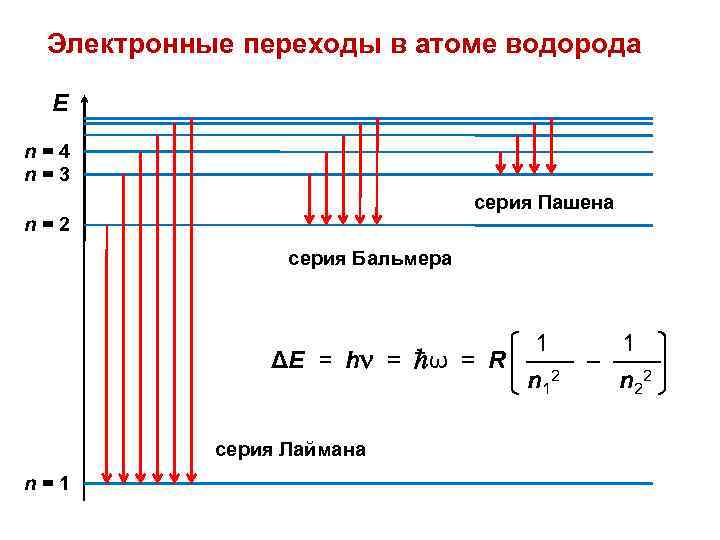Электронные переходы в атоме водорода Е n=4 n=3 серия Пашена n=2 серия Бальмера 1 1 ΔE = h = ω = R —— – —— n 12 n 22 серия Лаймана n=1

Вырожденность уровней энергии Е Е 3 = – R/9 Е 2 = – R/4 3 s 3 p+1 3 p 0 3 p– 1 2 s 3 d+2 3 d+1 3 d 0 3 d– 1 3 d– 2 2 p+1 2 p 0 2 p– 1 Степень вырождения = n 2 Е 1 = – R 1 s

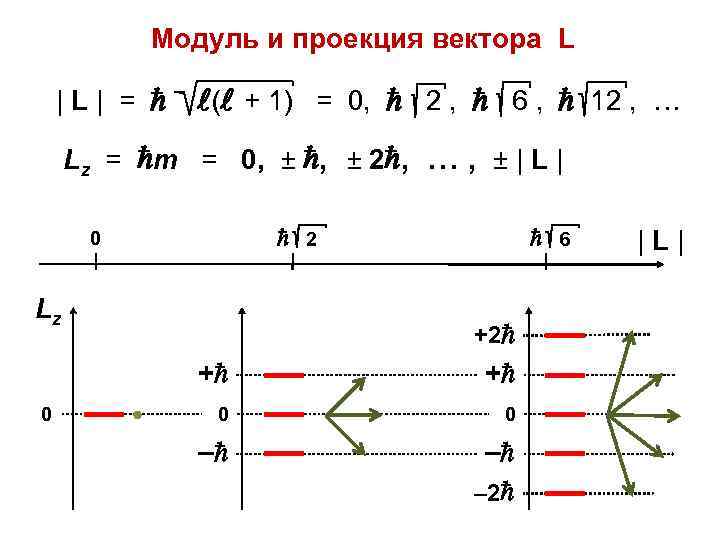Модуль и проекция вектора L |L| = ( + 1) = 0, 2 , 6 , 12 , … Lz = m = 0, ± 2 , … , ± | L | 2 0 Lz 6 +2 + 0 + 0 0 – – – 2 |L|

Пространственные наблюдаемые Ψ(r, θ, φ) — не является собственной для операторов координат R, Θ и Φ Ψ(r, θ, φ) = С 1 | C 1 |2 r 1 θ 1 φ1 = P(r 1, θ 1, φ1) | C 2 |2 = P(r 2, θ 2, φ2) …………. + С 2 r 2 θ 2 φ2 + …. Вероятностная функция распределения «электронное облако»

Вероятностная функция распределения «электронное облако»

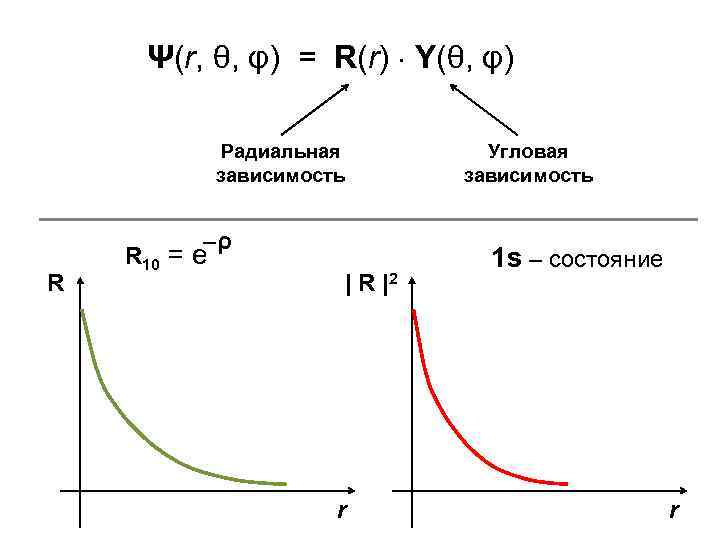Ψ(r, θ, φ) = R(r) Y(θ, φ) Радиальная зависимость –ρ R R 10 = e | R |2 r Угловая зависимость 1 s – состояние r

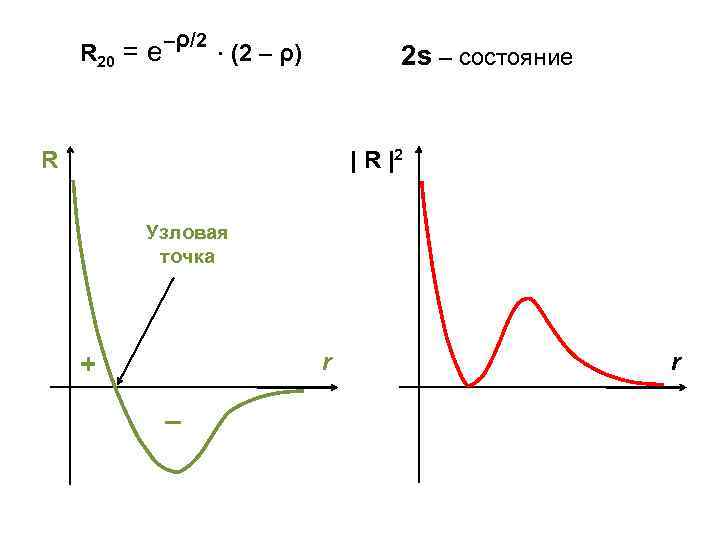R 20 = e –ρ/2 (2 – ρ) 2 s – состояние R |2 Узловая точка r + – r

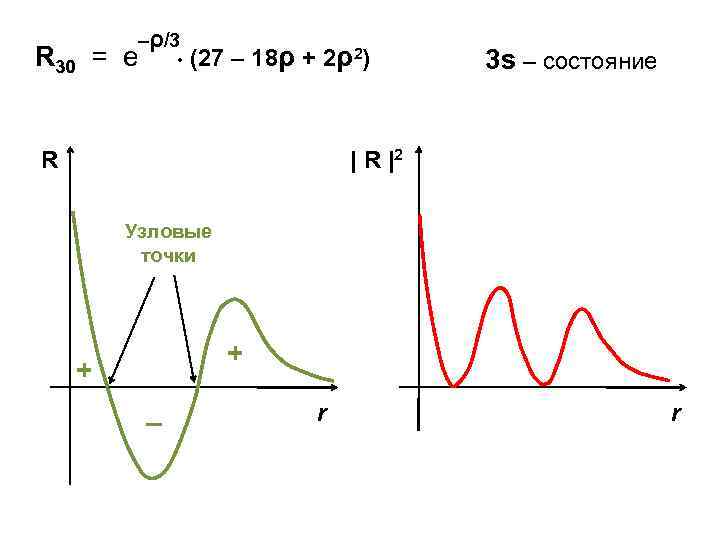–ρ/3 R 30 = e (27 – 18ρ + 2ρ2) R 3 s – состояние | R |2 Узловые точки + + – r r

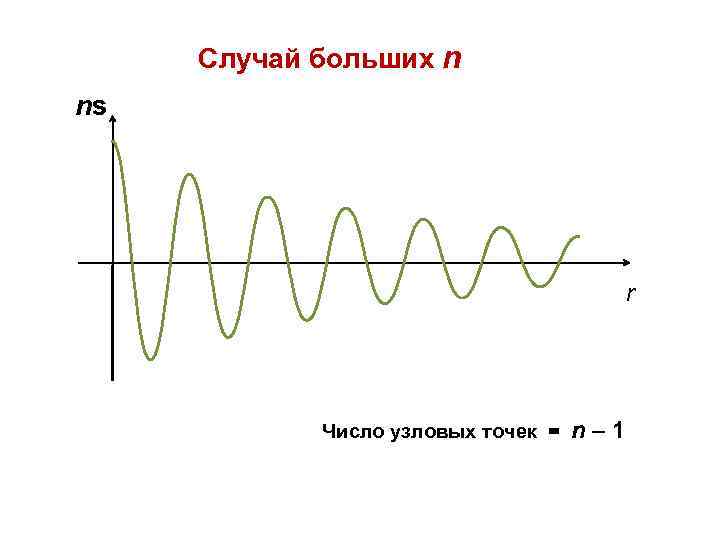Случай больших n ns r Число узловых точек = n– 1

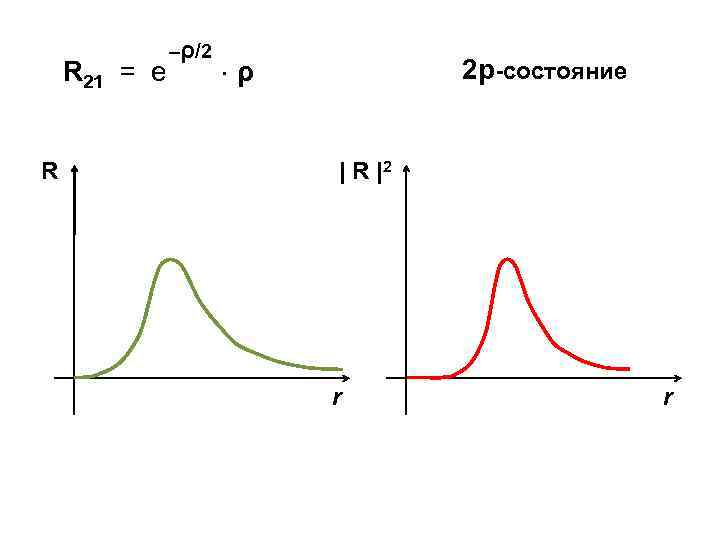R 21 = e R –ρ/2 ρ 2 р-состояние | R |2 r r

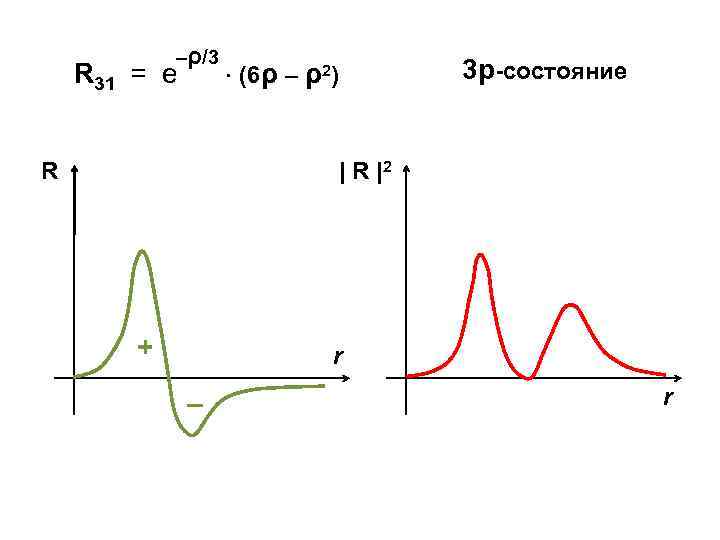–ρ/3 R 31 = e R 3 р-состояние (6ρ – ρ2) | R |2 + r – r

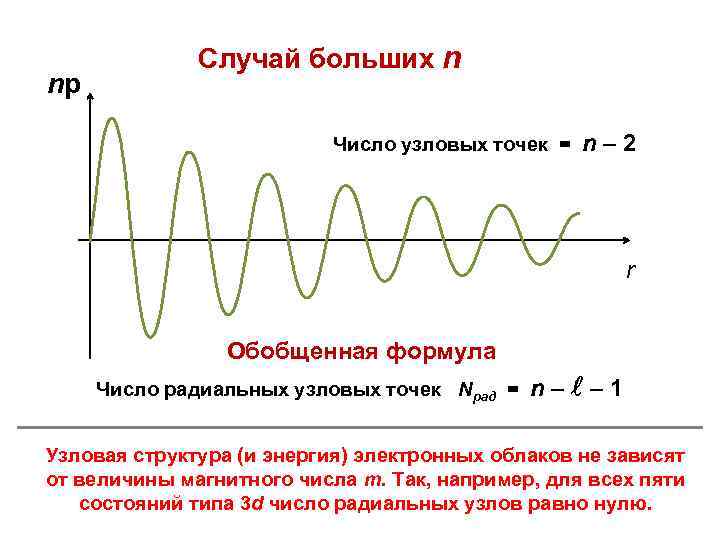nр Случай больших n Число узловых точек = n– 2 r Обобщенная формула Число радиальных узловых точек Nрад = n– – 1 Узловая структура (и энергия) электронных облаков не зависят от величины магнитного числа m. Так, например, для всех пяти состояний типа 3 d число радиальных узлов равно нулю.

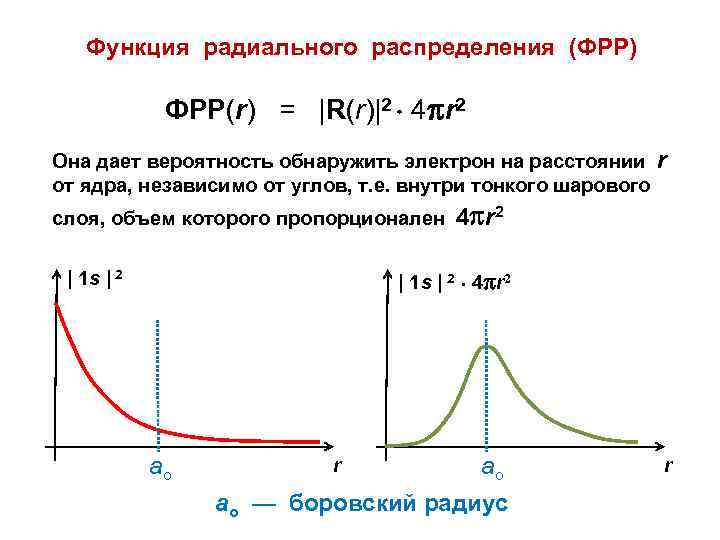Функция радиального распределения (ФРР) ФРР(r) = |R(r)|2 4 r 2 Она дает вероятность обнаружить электрон на расстоянии от ядра, независимо от углов, т. е. внутри тонкого шарового слоя, объем которого пропорционален r 4 r 2 | 1 s | 2 • 4 r 2 | 1 s | 2 ао r ао ао — боровский радиус r

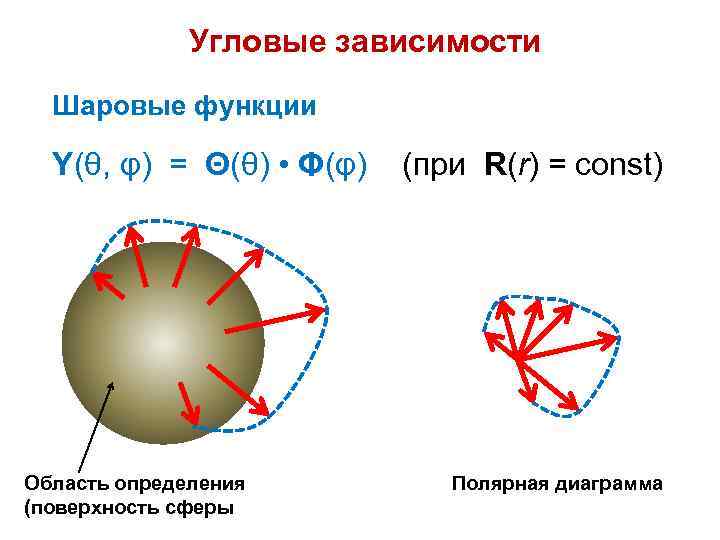Угловые зависимости Шаровые функции Y(θ, φ) = Θ(θ) • Φ(φ) Область определения (поверхность сферы (при R(r) = const) Полярная диаграмма

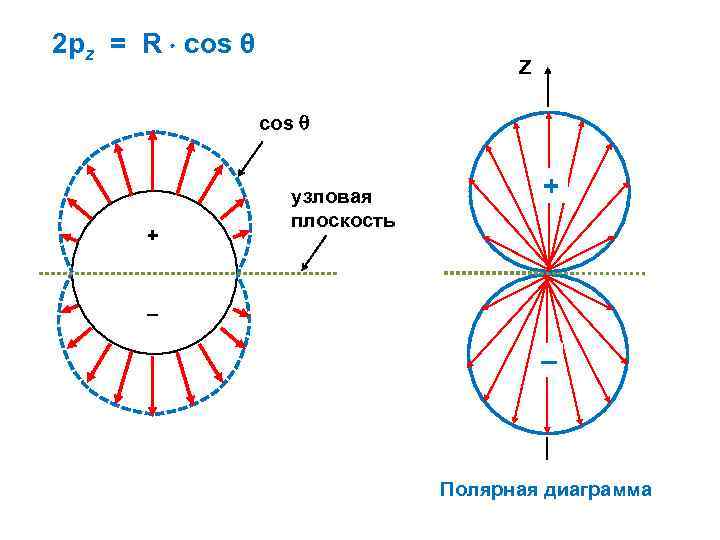2 рz = R cos θ Z cos + узловая плоскость + – – Полярная диаграмма

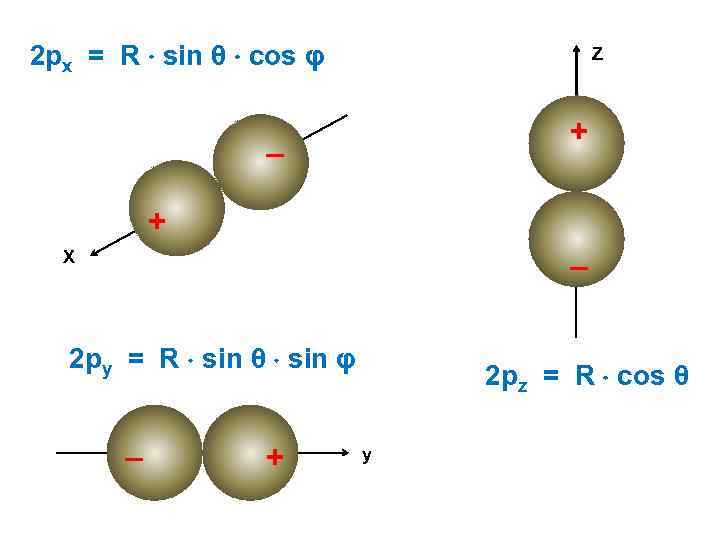2 рx = R sin θ cos φ Z + – + X – 2 рy = R sin θ sin φ – + 2 рz = R cos θ y

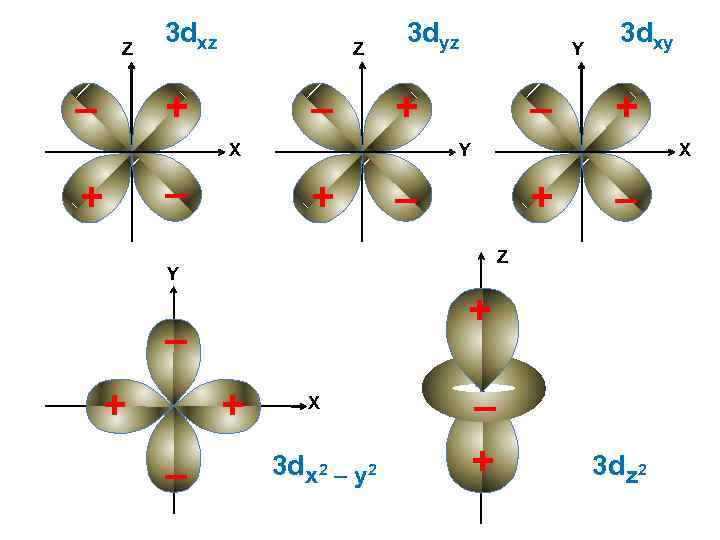Z – 3 dxz Z + – 3 dyz + X + – Y – + X – + – Z + – + Y Y + 3 dxy X 3 d x 2 – y 2 – + 3 d z 2

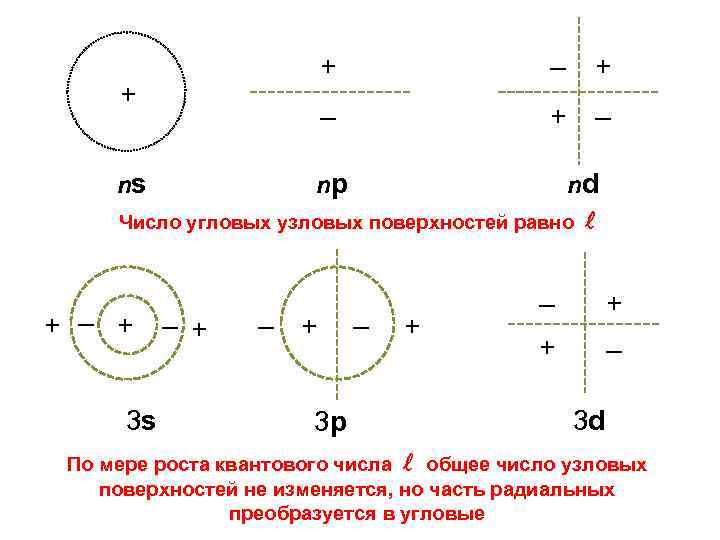+ ns + – + – nd Число угловых узловых поверхностей равно + – + 3 s np – + 3 p – + + – 3 d По мере роста квантового числа общее число узловых поверхностей не изменяется, но часть радиальных преобразуется в угловые

Изовероятные поверхности (ИВП) | Ψ(r, , ) |2 = const r = f ( , ) Для того, чтобы получить представление о распределении плотности электронного облака, необходимо располагать большим набором ИВП с разными значениями вероятности 2 рх Х ИВП – 90 % ИВП – 95 %

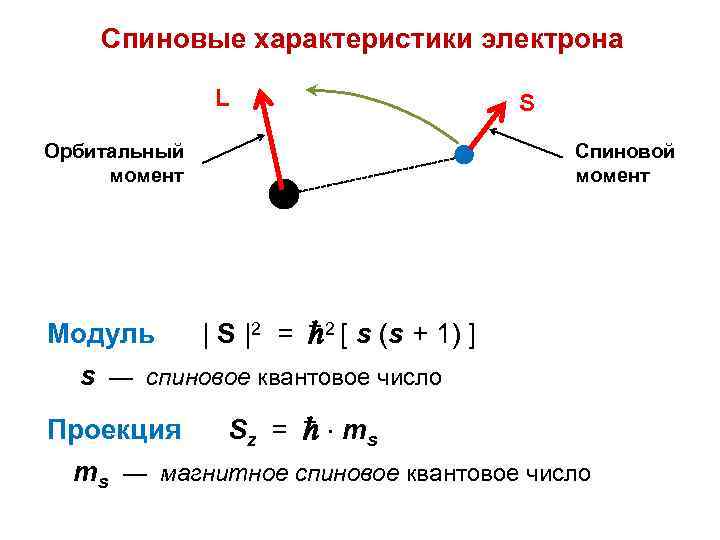Спиновые характеристики электрона L Орбитальный момент S Спиновой момент Модуль | S |2 = 2 [ s (s + 1) ] s — спиновое квантовое число Проекция S z = ms ms — магнитное спиновое квантовое число

s = 1/2 ms = ( +1/2; – 1/2 ) Спиновые состояния электрона -состояние m. S = – 1/2 m. S = +1/2 SZ = – /2 (SZ) SZ = + /2 Ψ(r, θ, φ) Ψ(r, θ, φ, ) = Ψ(r, θ, φ) ( ) Пространственный множитель Спиновой множитель

Квантовые числа { n, , m , s, ms } { n, , m } {s, ms } Ψ(r, θ, φ, ) = Ψ(r, θ, φ) ( ) Атомная спин-орбиталь (АСО) Атомная орбиталь (АО) s = const | S | = const Наблюдаемые { n, , m , s, ms } { E, | L |, LZ, | S |, SZ } { n, , m , m s } { E, | L |, LZ, SZ }

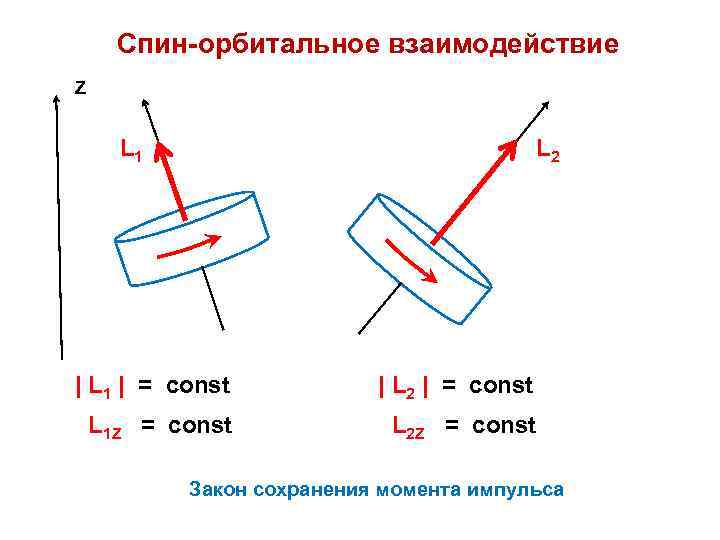Спин-орбитальное взаимодействие Z L 1 L 2 | L 1 | = const | L 2 | = const L 1 Z = const L 2 Z = const Закон сохранения момента импульса

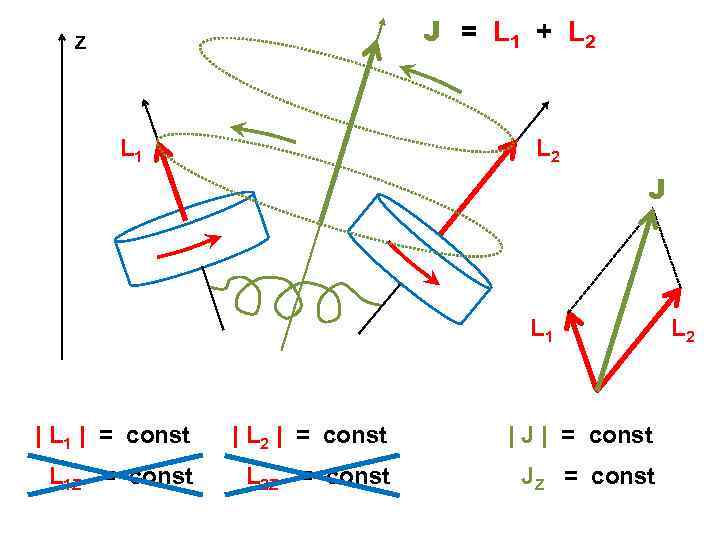J = L 1 + L 2 Z L 1 L 2 J L 1 | = const | L 2 | = const | J | = const L 1 Z = const L 2 Z = const JZ = const L 2

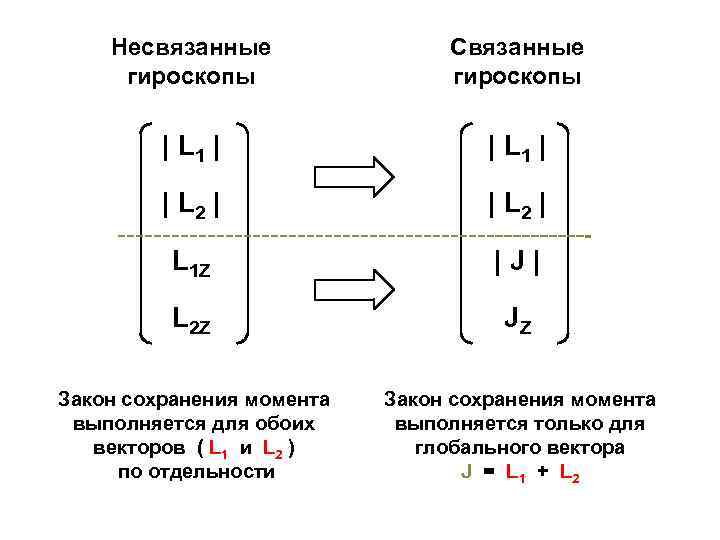Несвязанные гироскопы Cвязанные гироскопы | L 1 | | L 2 | L 1 Z |J| L 2 Z JZ Закон сохранения момента выполняется для обоих векторов ( L 1 и L 2 ) по отдельности Закон сохранения момента выполняется только для глобального вектора J = L 1 + L 2

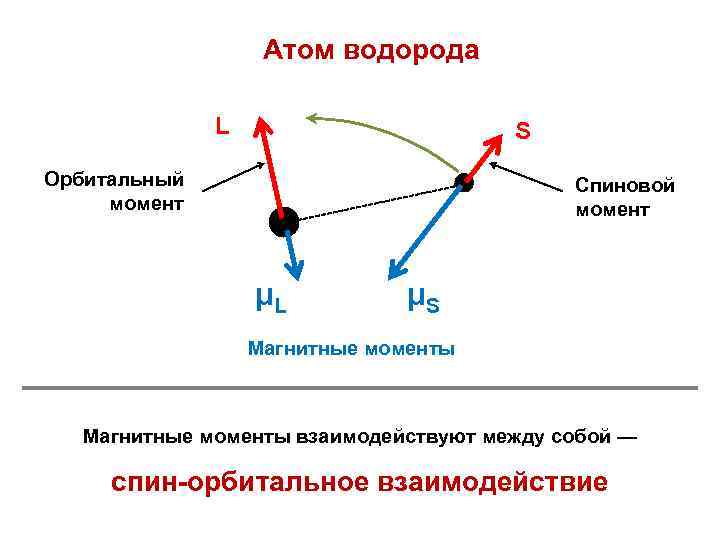Атом водорода L S Орбитальный момент Спиновой момент μL μS Магнитные моменты взаимодействуют между собой — спин-орбитальное взаимодействие

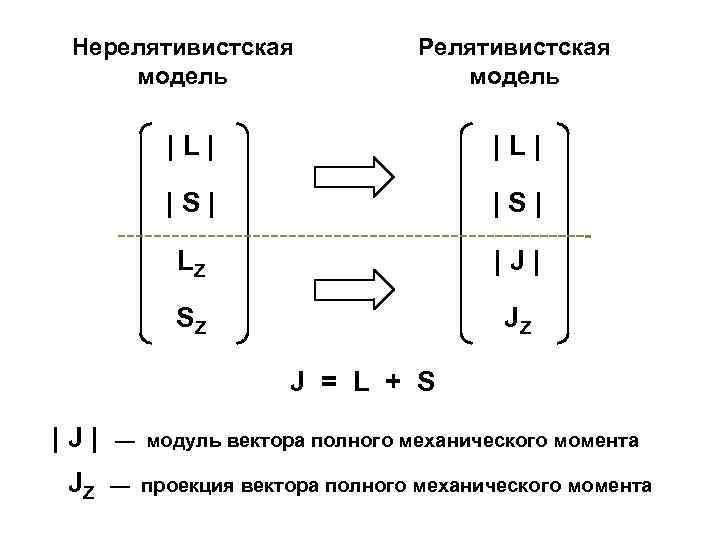Нерелятивистская модель Релятивистская модель |L| |S| LZ |J| SZ JZ J = L + S |J| — модуль вектора полного механического момента JZ — проекция вектора полного механического момента

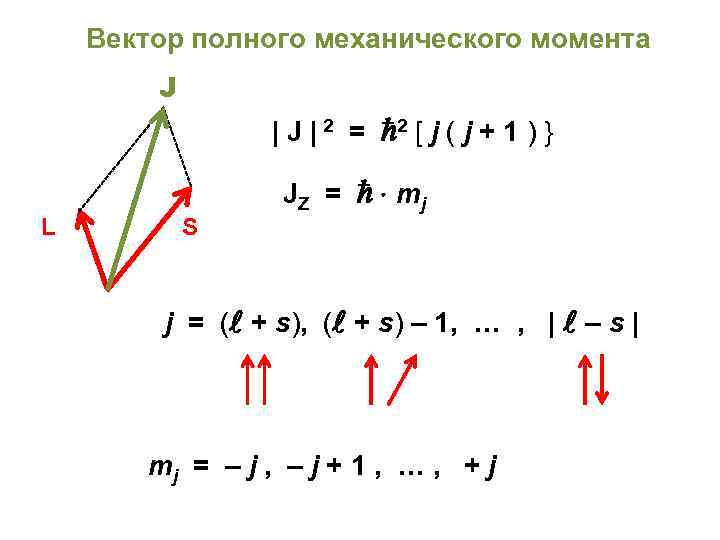Вектор полного механического момента J | 2 = 2 [ j ( j + 1 ) } L S JZ = mj j = ( + s), ( + s) – 1, … , | – s | mj = – j , – j + 1 , … , + j

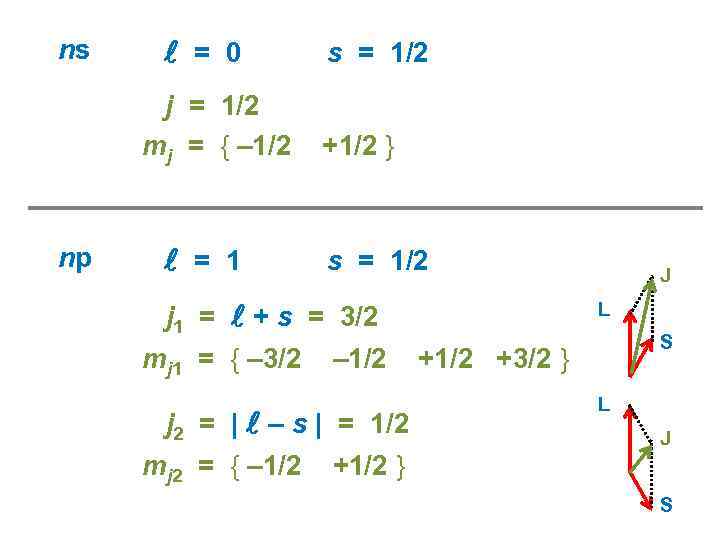ns = 0 j = 1/2 mj = { – 1/2 np = 1 s = 1/2 +1/2 } s = 1/2 j 1 = + s = 3/2 mj 1 = { – 3/2 – 1/2 j 2 = | – s | = 1/2 mj 2 = { – 1/2 +1/2 } J L S +1/2 +3/2 } L J S

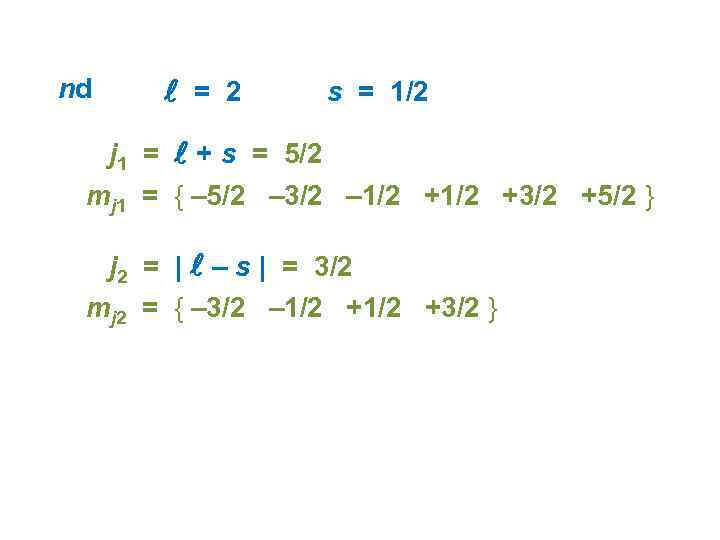nd = 2 s = 1/2 j 1 = + s = 5/2 mj 1 = { – 5/2 – 3/2 – 1/2 +3/2 +5/2 } j 2 = | – s | = 3/2 mj 2 = { – 3/2 – 1/2 +3/2 }

Нерелятивистские состояния { n, , m , s, ms } { E, | L |, LZ, | S |, SZ } { n, , m , m s } { E, | L |, LZ, SZ } Релятивистские состояния { n, , s, j, mj } { E, | L |, | S |, | J |, JZ } Нерелятивистская номенклатура n { n, , mj } { E, | L |, | J |, JZ } Релятивистская номенклатура 2 s+1 m j, j

m = – 1 2 so 1 so 0 +1 2 p– 1 2 po 2 p+1 ms = +1/2 2 p– 1 2 po 2 p+1 ms = – 1/2 0 +1 m = – 1 mj = – 3/2 2 s 2 s 2 p 1/2 3/2 – 1/2 +3/2 2 p 1/2 2 p mj = – 1/2 +1/2 3/2 j = 1/2

m = – 2 – 1 0 +1 +2 3 d– 1 3 po 3 d+1 3 d+2 ms = +1/2 3 d– 1 3 do 3 d+1 3 d+2 ms = – 1/2 – 1 0 +1 +2 m = – 2 mj = – 5/2 2 d 5/2 – 3/2 2 d 2 d mj = – 1/2 +3/2 +5/2 2 d 5/2 2 d 3/2 – 3/2 – 1/2 +3/2 5/2 j = 3/2

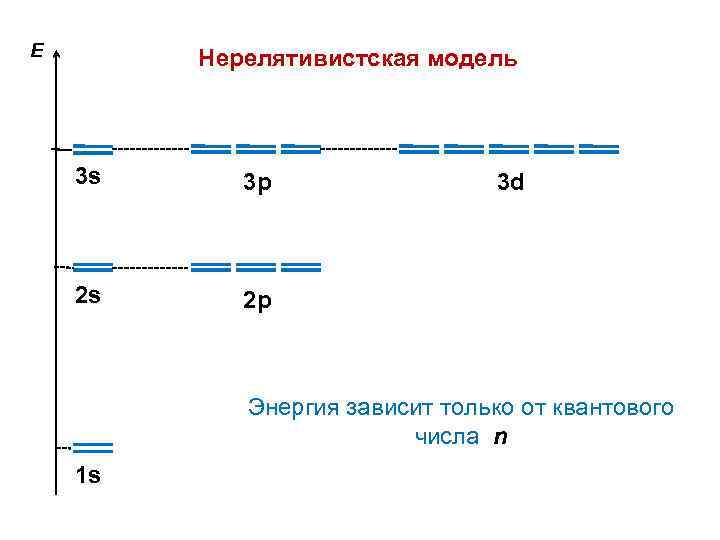E Нерелятивистская модель 3 s 3 p 2 s 2 p 3 d Энергия зависит только от квантового числа n 1 s

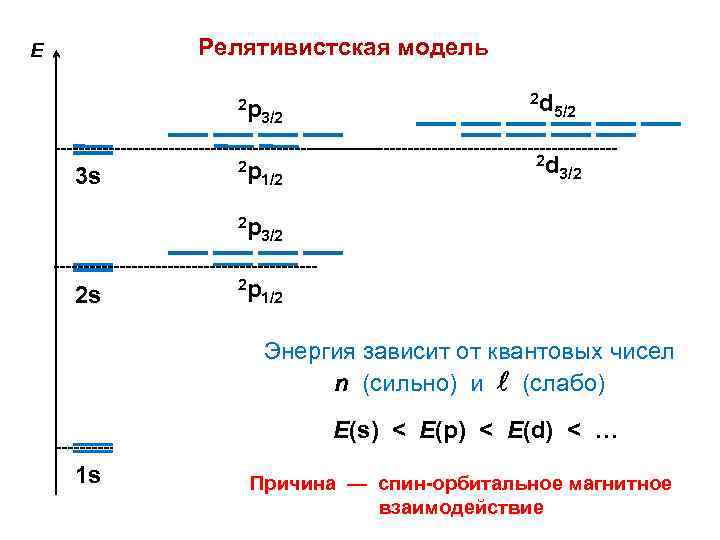Релятивистская модель E 2 p 3/2 2 s 1/2 2 p 3 s 2 p 5/2 2 d 3/2 2 p 2 d 1/2 3/2 Энергия зависит от квантовых чисел n (сильно) и (слабо) Е(s) < E(p) < E(d) < … 1 s Причина — спин-орбитальное магнитное взаимодействие

Домашнее задание Задача 6. 1. Описать графически радиальные и угловые зависимости волновой функции и плотности электронного облака для заданного стационарного состояния { n, , ms } атома Н: определить число радиальных и угловых узловых поверхностей Nрадиальн. = ? ? ? , Nуглов. = ? ? ? нарисовать примерный вид графиков радиальной и угловой зависимостей волновой функции и ее квадрата. Радиальные Угловые

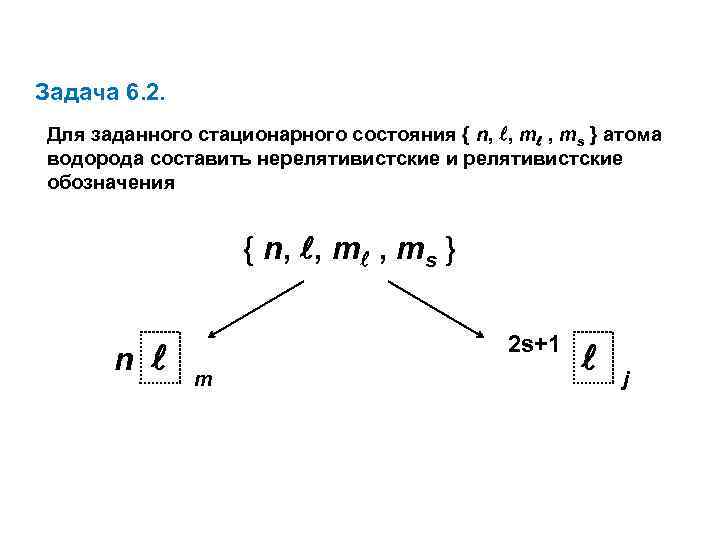Задача 6. 2. Для заданного стационарного состояния { n, , ms } атома водорода составить нерелятивистские и релятивистские обозначения { n, , ms } n 2 s+1 m j

Задача 6. 3. Для заданного стационарного состояния { n, , ms } атома водорода вычислить значения наблюдаемых: энергии (в Дж) Е = ? ? ? модулей и проекций векторов орбитального, спинового и полного механического моментов (в Дж с) | L | = ? ? ? LZ = ? ? ? | S | = ? ? ? SZ = ? ? ? | J 1 | = ? ? ? J 1 Z = ? ? ? ( 2 j 1 + 1 штука ) | J 2 | = ? ? ? J 2 Z = ? ? ? ( 2 j 2 + 1 штука ) j 1 = + s j 2 = | – s |