Atom-centered Density Matrix Propagation ADMP Theory and Applications

Atom-centered Density Matrix Propagation (ADMP): Theory and Applications Srinivasan S. Iyengar Department of Chemistry and Department of Physics, Indiana University

Iyengar Group, Indiana University Outline Ø Brief discussion of ab initio molecular dynamics Ø Atom-centered (ADMP) Density Matrix Propagation • Nut-n-bolts issues Ø Some Results: • Novel findings for protonated water clusters • QM/MM generalizations: ion channels • Gas phase reaction dynamics

Iyengar Group, Indiana University Molecular dynamics on a single potential surface Ø Parameterized force fields (e. g. AMBER, CHARMM) • • • Energy, forces: parameters obtained from experiment Molecular motion: Newton’s laws Works for large systems – But hard to parameterize bond-breaking/formation (chemical reactions) – Issues with polarization/charge transfer/dynamical effects Ø Born-Oppenheimer (BO) Dynamics • • • Ø Solve electronic Schrödinger eqn (DFT/HF/post-HF) for each nuclear structure Nuclei propagated using gradients of energy (forces) Works for bond-breaking but computationally expensive Large reactive, polarizable systems: Something like BO, but preferably less expensive.

Iyengar Group, Indiana University Extended Lagrangian dynamics Ø Circumvent Computational Bottleneck of BO • • Ø Avoid repeated SCF: electronic structure, not converged, but propagated “Simultaneous” propagation of electronic structure and nuclei: adjustment of time-scales Car-Parrinello (CP) method • • Orbitals expanded in plane waves Occupied orbital coefficients propagated – O(N 3) computational scaling (traditionally) – O(N) with more recent Wannier representations (? ) Ø Atom-centered Density Matrix Propagation (ADMP) • • Atom-centered Gaussian basis functions Electronic Density Matrix propagated – Asymptotic linear-scaling with system size • • Allows the use of accurate hybrid density functionals suitable for clusters References… CP: R. Car, M. Parrinello, Phys. Rev. Lett. 55 (22), 2471 (1985). ADMP: Schlegel, et al. JCP, 114, 9758 (2001). Iyengar, et al. JCP, 115, 10291 (2001). Iyengar et al. Israel J. Chem. 7, 191, (2002). Schlegel et al. JCP 114, 8694 (2002). Iyengar and Frisch JCP 121, 5061 (2004).

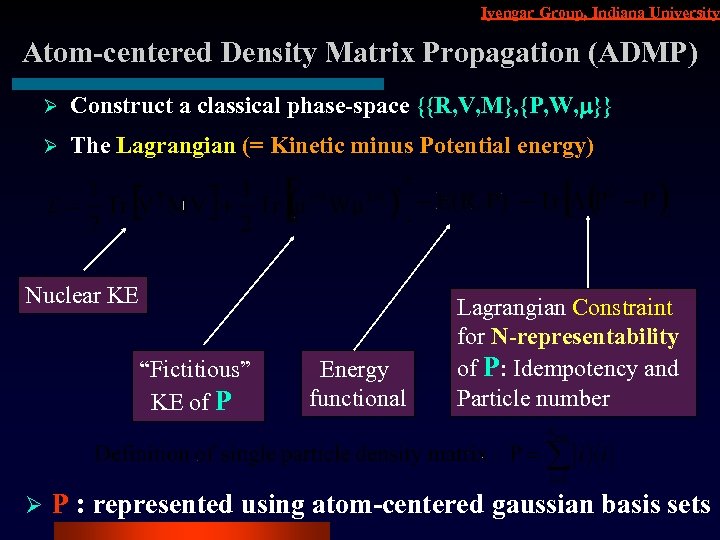Iyengar Group, Indiana University Atom-centered Density Matrix Propagation (ADMP) Ø Construct a classical phase-space {{R, V, M}, {P, W, m}} Ø The Lagrangian (= Kinetic minus Potential energy) Nuclear KE “Fictitious” KE of P Ø Energy functional Lagrangian Constraint for N-representability of P: Idempotency and Particle number P : represented using atom-centered gaussian basis sets

Iyengar Group, Indiana University Euler-Lagrange equations of motion for ADMP Ø Equations of motion for density matrix and nuclei acceleration of density matrix, P “Fictitious” mass of P Force on P Classical dynamics in {{R, V, M}, {P, W, m}} phase space Ø Next few slide: Forces, propagation equations, formal error analysis Ø

Iyengar Group, Indiana University Nuclear Forces: What Really makes it work Hellman-Feynman contributions Contributions due to [F, P] 0. Part of non-Hellman-Feynman Pulay’s moving basis terms S=UTU, Cholesky or Löwdin

Iyengar Group, Indiana University Density Matrix Forces: Ø Use Mc. Weeny Purified DM (3 P 2 -2 P 3) in energy expression to obtain

Iyengar Group, Indiana University m effects an adjustment of time-scales: Direction of Increasing Frequency of m : P changes slower with time: characteristic frequency adjusted Ø But Careful - too large m: non-physical Ø Appropriate m: approximate BO dynamics Ø Consequence Bounds for m: From a Hamiltonian formalism Ø m: also related to deviations from the BO surface Ø

Iyengar Group, Indiana University “Physical” interpretation of m : Bounds Ø Commutator of the electronic Hamiltonian and density matrix: bounded by magnitude of m Ø Magnitude of m : represents deviation from BO surface Ø m acts as an “adiabatic control parameter” Reference… Iyengar et al. Israel J. Chem. 7, 191, (2002).

Iyengar Group, Indiana University Bounds on the magnitude of m : Ø The Lagrangian Ø The Conjugate Hamiltonian (Legendre Transform) Controlling m: Deviations from BO surface and adiabaticity Reference… Iyengar et al. JCP. 115, 10291 (2001).

Iyengar Group, Indiana University Comparison with BO dynamics Ø Born-Oppenheimer dynamics: • Converged electronic Ø ADMP: • states. • • Approx. 8 -12 SCF cycles / nuclear config. d. E/d. R not same in both methods • • Electronic state propagated classically : no convergence reqd. 1 SCF cycle : for Fock matrix -> d. E/d. P Current: 3 -4 times faster. References… Iyengar et al. Israel J. Chem. 7, 191, (2002). Schlegel et al. JCP 114, 8694 (2002). Iyengar and Frisch JCP 121, 5061 (2004).

Iyengar Group, Indiana University Propagation of P: time-reversible propagation Ø Velocity Verlet propagation of P Ø Propagation of W Ø Classical dynamics in {{R, V}, {P, W}} phase space Ø Li and Li+1 obtained iteratively: – Conditions: Pi+1 2 = Pi+1 and Wi. Pi + Pi. Wi = Wi (next two slides)

Iyengar Group, Indiana University Idempotency (N-Representibility of DM): Ø Given Pi 2 = Pi, need Li to find idempotent Pi+1 Ø Solve iteratively: Pi+12 = Pi+1 Ø Given Pi, Pi+1, Wi+1/2, need Li+1 to find Wi+1 Ø Solve iteratively: Wi+1 Pi+1 + Pi+1 Wi+1 = Wi+1

Iyengar Group, Indiana University Idempotency: To obtain Pi+1 Given Pi 2 = Pi, need to find indempotent Pi+1 Ø Guess: Ø Or guess: Ø Iterate Pi+1 to satisfy Pi+12 = Pi+1 Ø Ø Rational for choice Pi. TPi + Qi. TQi above:

Iyengar Group, Indiana University Idempotency: To obtain Wi+1 Given Wi. Pi + Pi. Wi = Wi, find appropriate Wi+1 Ø Guess: Ø Ø Iterate Wi+1 to satisfy Wi+1 Pi+1 + Pi+1 Wi+1 = Wi+1

Iyengar Group, Indiana University How it all works … Ø Initial config. : R(0). Converged SCF: P(0) Ø Initial velocities V(0) and W(0) : flexible Ø P(Dt), W(Dt) : from analytical gradients and idempotency Ø Similarly for R(Dt) Ø And the loop continues…

Iyengar Group, Indiana University Protonated Water Clusters Ø Important systems for: • • Ø Ion transport in biological and condensed systems Enzyme kinetics Acidic water clusters: Atmospheric interest Electrochemistry Experimental work: • • • Mass Spec. : Castleman IR: M. A. Johnson, Mike Duncan, M. Okumura Sum Frequency Generation (SFG) : Y. R. Shen, M. J. Schultz and coworkers Lots of theory too: Jordan, Mc. Coy, Bowman, Klein, Singer (not exhaustive by any means. . ) Ø Variety of medium-sized protonated clusters using ADMP Ø References… ADMP treatment of protonated water clusters: Iyengar, et al. JCP, 123, 084309 (2005). Iyengar et al. Int. J. Mass Spec. 241, 197 (2005). Iyengar JCP 123, 084310, (2005).

Protonated Water Clusters: Iyengar Group, Indiana University Hopping via the Grotthuss mechanism True for 20, 30, 40, 50 and larger clusters…

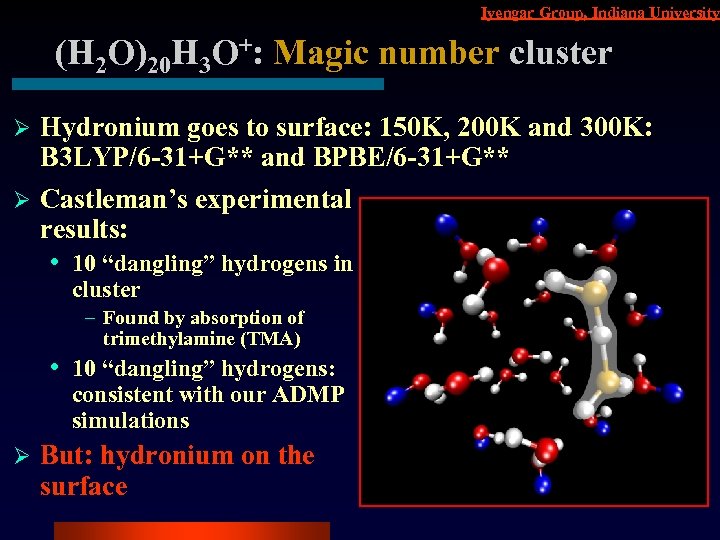Iyengar Group, Indiana University (H 2 O)20 H 3 O+: Magic number cluster Hydronium goes to surface: 150 K, 200 K and 300 K: B 3 LYP/6 -31+G** and BPBE/6 -31+G** Ø Castleman’s experimental results: Ø • • Ø 10 “dangling” hydrogens in cluster – Found by absorption of trimethylamine (TMA) 10 “dangling” hydrogens: consistent with our ADMP simulations But: hydronium on the surface

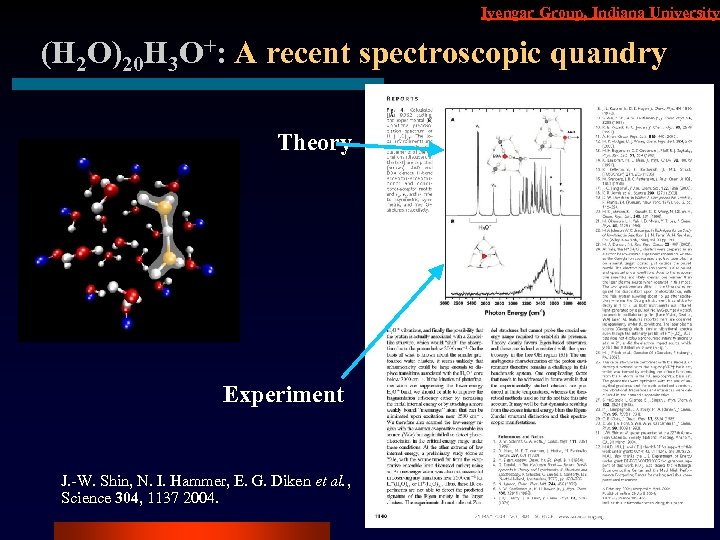Iyengar Group, Indiana University (H 2 O)20 H 3 O+: A recent spectroscopic quandry Theory Experiment J. -W. Shin, N. I. Hammer, E. G. Diken et al. , Science 304, 1137 2004.

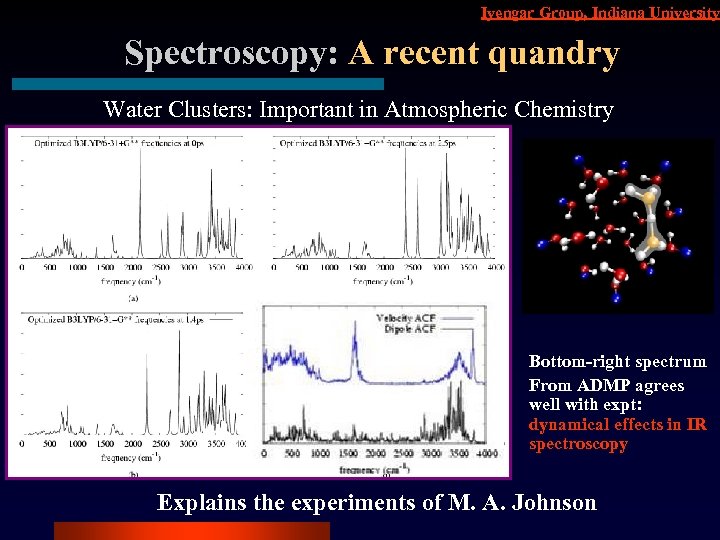Iyengar Group, Indiana University Spectroscopy: A recent quandry Water Clusters: Important in Atmospheric Chemistry Bottom-right spectrum From ADMP agrees well with expt: dynamical effects in IR spectroscopy Explains the experiments of M. A. Johnson

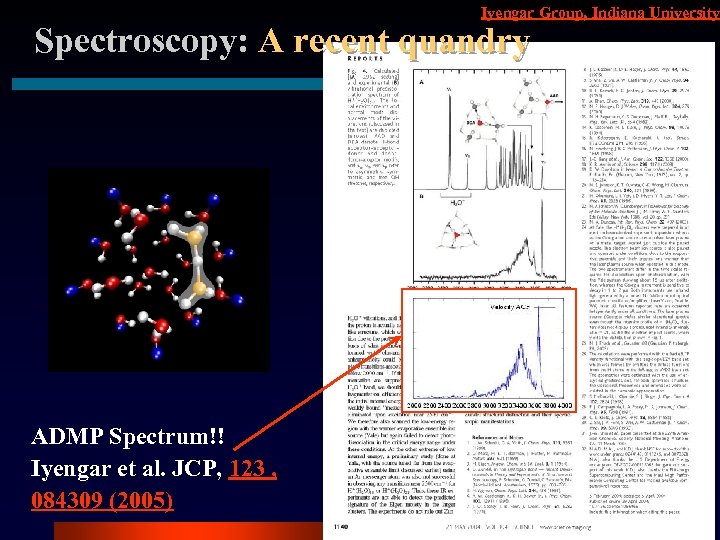Iyengar Group, Indiana University Spectroscopy: A recent quandry ADMP Spectrum!! Iyengar et al. JCP, 123 , 084309 (2005)

Iyengar Group, Indiana University (H 2 O)20 H 3 O+: Magic number cluster Hydronium goes to surface: 150 K, 200 K and 300 K: B 3 LYP/6 -31+G** and BPBE/6 -31+G** Ø Castleman’s experimental results: Ø • • Ø 10 “dangling” hydrogens in cluster – Found by absorption of trimethylamine (TMA) 10 “dangling” hydrogens: consistent with our ADMP simulations But: hydronium on the surface

Iyengar Group, Indiana University Larger Clusters and water/vacuum interfaces: Similar results

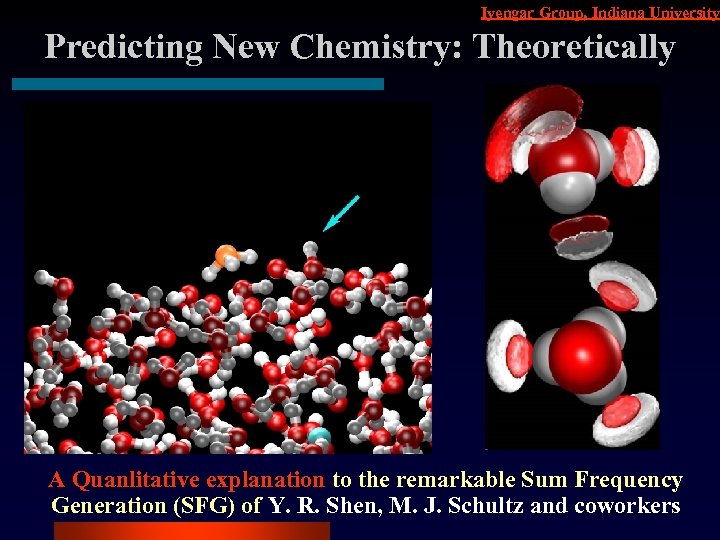Iyengar Group, Indiana University Predicting New Chemistry: Theoretically A Quanlitative explanation to the remarkable Sum Frequency Generation (SFG) of Y. R. Shen, M. J. Schultz and coworkers

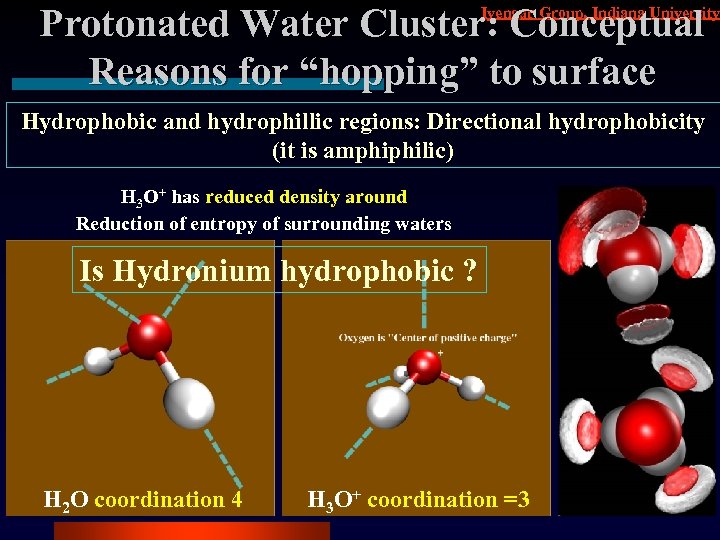Protonated Water Cluster: Conceptual Reasons for “hopping” to surface Iyengar Group, Indiana University Hydrophobic and hydrophillic regions: Directional hydrophobicity (it is amphiphilic) H 3 O+ has reduced density around Reduction of entropy of surrounding waters Is Hydronium hydrophobic ? H 2 O coordination 4 H 3 O+ coordination =3

Iyengar Group, Indiana University Experimental results suggest this as well Ø Y. R. Shen: Sum Frequency Generation (SFG) • • • IR for water/vapor interface shows dangling O-H bonds intensity substantially diminishes as acid conc. is increased Consistent with our results – Hydronium on surface: lone pair outwards, instead of dangling O-H • Ø acid concentration is higher on the surface Schultz and coworkers: acidic moieties alter the structure of water/vapor interfaces References… P. B. Miranda and Y. R. Shen, J. Phys. Chem. B, 103, 3292 -3307 (1999). M. J. Schultz, C. Schnitzer, D. Simonelli and S. Baldelli, Int. Rev. Phys. Chem. 19, 123 -153 (2000)

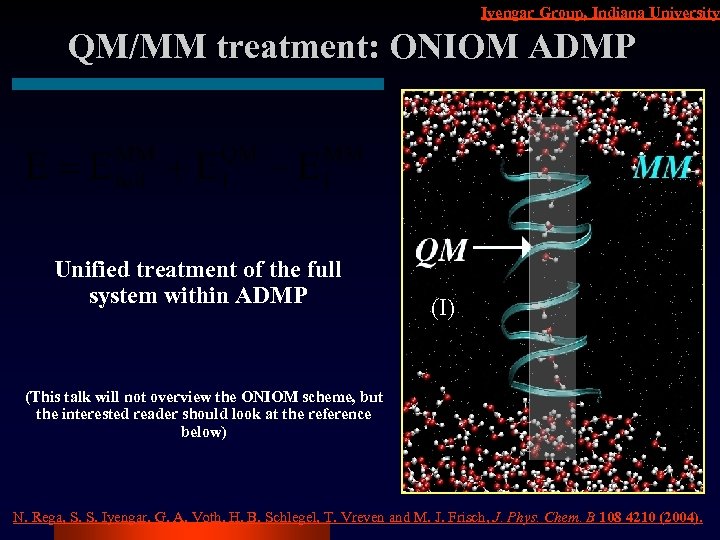Iyengar Group, Indiana University QM/MM treatment: ONIOM ADMP Unified treatment of the full system within ADMP (I) (This talk will not overview the ONIOM scheme, but the interested reader should look at the reference below) N. Rega, S. S. Iyengar, G. A. Voth, H. B. Schlegel, T. Vreven and M. J. Frisch, J. Phys. Chem. B 108 4210 (2004).

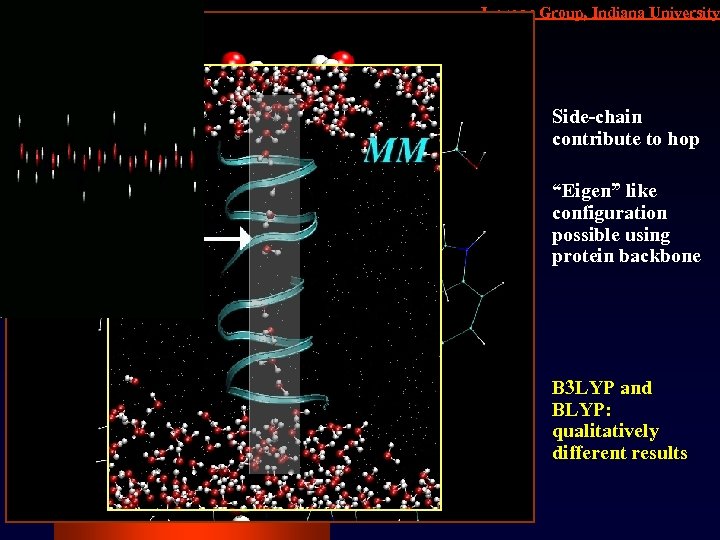Iyengar Group, Indiana University Side-chain contribute to hop “Eigen” like configuration possible using protein backbone B 3 LYP and BLYP: qualitatively different results

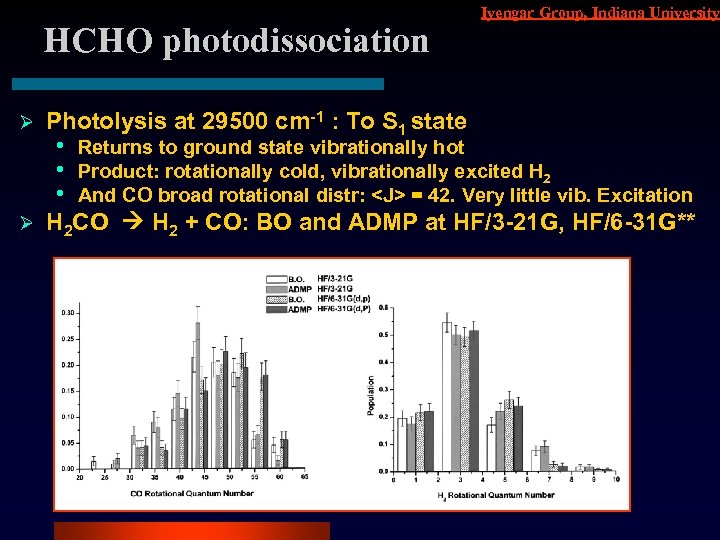HCHO photodissociation Ø Ø Iyengar Group, Indiana University Photolysis at 29500 cm-1 : To S 1 state • • • Returns to ground state vibrationally hot Product: rotationally cold, vibrationally excited H 2 And CO broad rotational distr: = 42. Very little vib. Excitation H 2 CO H 2 + CO: BO and ADMP at HF/3 -21 G, HF/6 -31 G**

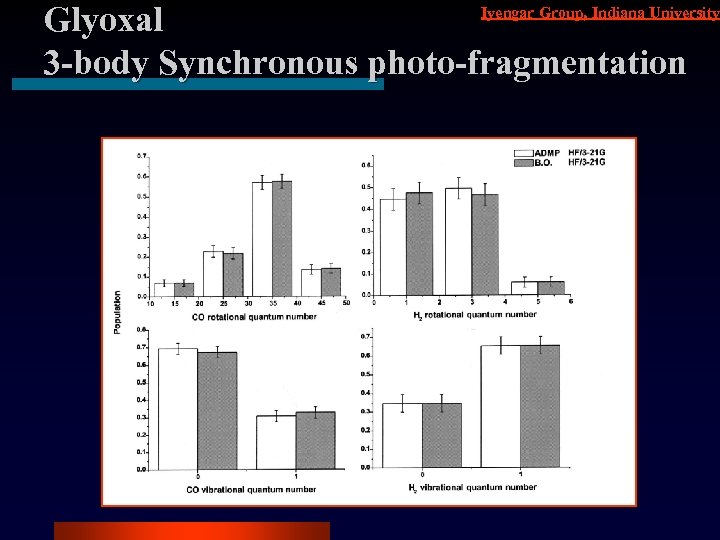Iyengar Group, Indiana University Glyoxal 3 -body Synchronous photo-fragmentation

Iyengar Group, Indiana University Conclusions Ø ADMP: powerful approach to ab initio molecular dynamics • Linear scaling with system size • Hybrid (more accurate) density functionals • Smaller values for fictitious mass allow – treatment of systems with hydrogens is easy (no deuteriums required) – greater adiabatic control (closer to BO surface) Ø Examples bear out the accuracy of the method

Iyengar Group, Indiana University Acknowledgment Ø The work has enormously benefited from my former advisors and collaborators: – – Ø Greg Voth Berny Schlegel Gus Scuseria Mike Frisch At IU, people contributing to this work are: – – Jacek Jakowski (post-doc) Isaiah Sumner (grad student) Xiaohu Li (grad student) Virginia E. Teige (Freshman)