At the end of this lecture you should

At the end of this lecture you should • Understand that a wave is a means of transferring energy by means of an oscillation or vibration • Have a qualitative and quantitative understanding of what a periodic function is • Understand what is meant by transverse wave and longitudinal wave • Understand what is meant by a mechanical wave and by an electromagnetic wave • Be able to give examples of some physical quantities which propagate as waves • Be able to give one mathematical expression for a wave traveling in one dimension • Be able to define the terms wavelength, period, frequency, crest, trough, amplitude and velocity for a wave and be comfortable using the equation v=f • Understand what is meant by the phase of a wave and what a phase shift or phase constant is.

Waves : Basic concepts What is a progressive or travelling wave? Such a wave transfers energy without …………… Examples of progressive waves ……………… .

Transverse waves In a transverse wave, the direction of vibration of each particle (or field) is perpendicular to the direction of the motion of the wave. Examples of transverse waves:

Longitudinal waves In a longitudinal wave… Example of longitudinal waves:

Mechanical and electromagnetic waves A mechanical wave requires… Eg An EM wave…. . . . Eg

Mathematical representation of a progressive wave The simplest wave is sinusoidal Let x be the distance measured in the direction of travel and y the particle displacement. Suppose that at x = 0 , y = 0.

An equation representing such a wave at some instant of time is: A is the amplitude and λ is the wavelength Y X

How do we represent a moving wave mathematically? Consider: a graph of f(x) against x a graph of f(x – a) against x a graph of f(x – vt) against x

Mathematical representation of progressive wave The period T of the wave is the time for one wavelength of the wave to pass a given point. Then: The frequency of a wave is the number of complete waves passing a given point in a second

Example 1 What is the frequency of visible light of wavelength 0. 500 μm

There are several ways to express this wave equation e. g. substitute for v using we obtain: It is convenient to define the wave-number k and angular frequency ω as

Hence we can express the wave-function as If we want the wave to travel in the negative x direction the x and t coefficients must have the same sign e. g.

If we “look” at one point along the wave then x becomes a constant and we have: This shows that a particle at that point in the wave is moving with SHM Important: The wave moves with constant velocity , but all the particles in the wave are moving with SHM. The period of the SHM is the same as the period of the wave.

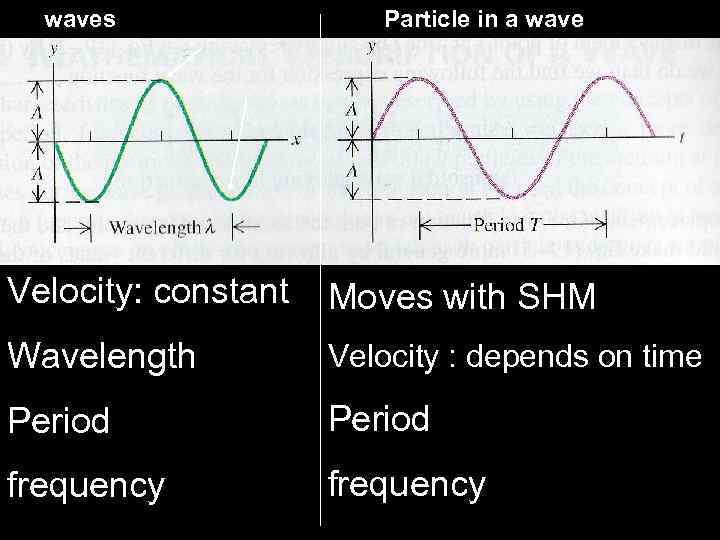waves Particle in a wave Velocity: constant Moves with SHM Wavelength Velocity : depends on time Period frequency

Example 2 A sinusoidal transverse wave on a stretched string has an amplitude of 2. 00 m, a wavelength of 4. 00 m, and a period of 8. 00 s. It is moving in the positive x direction. Assume y = 0 at t = 0 and at x = 0. Sketch a graph of this wave at t = 0, showing the vertical displacement y against distance x in direction of motion. Show one complete wavelength.

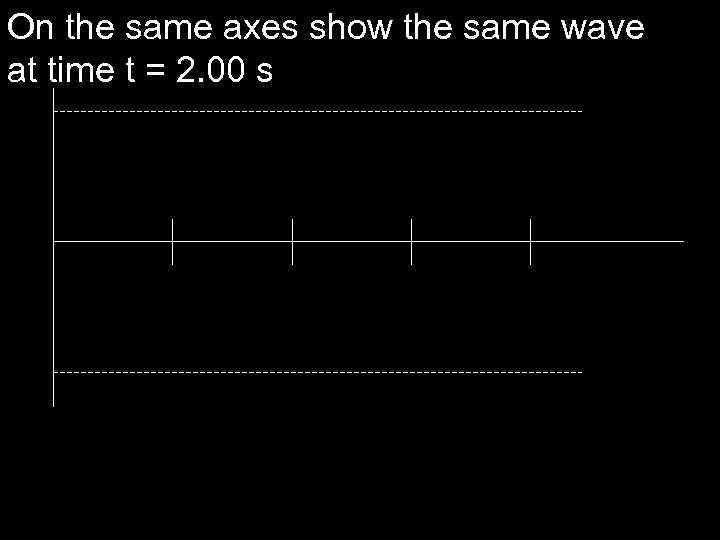On the same axes show the same wave at time t = 2. 00 s

Example 3 For the same transverse wave as in example 2, plot a graph of displacement against time for a point 2. 00 m in the direction of motion. Show one complete cycle (period).

Example 4 • For the same transverse wave find a) the speed of the wave b) the maximum speed of a particle in the string c) the maximum acceleration of a particle in the string Reminder: A = 2. 00 m, λ = 4. 00 m, T =8. 00 s

Phase For a wave function y(x, t) = Asin(kx – ωt), the part (kx – ωt) is called the phase. If another wave has the function y(x, t) = Asin(kx – ωt + φ), we call φ the phase shift or phase difference.

Two waves are in phase if their crests and/or troughs always arrive a point together. This is an example of constructive interference. Note: for a wave moving from a less dense to a more dense medium, the reflected wave undergoes a phase change of 180˚ at the boundary (due to Newton’s third law). Conversely, for a wave moving from a more dense medium to a less dense medium, there is no phase change in the reflected wave.

Test three • Based on CW 5 -6 and materials on errors from PSC classes • Please go to the same test place as for test two. Please arrive there at 1. 55 pm. The test will last 70 minutes.

Office hours & Project marks • Sign up – now – for appointments with teachers on Tuesday, Thursday and Friday this week. Sign up sheets outside physics office. • Group leaders need to submit a folder of any photos and a maximum of one video taken during the project work. Please pass on your flash drive to your PSC teacher for copying by Friday, December 2 nd 2011. • All project marks will be given to students in January 2012. The marking will take time; e. g. it involves Steve marking 311 learner diaries and 63 project reports.

READING • • Adams and Allday: 6. 1 At the end of this lecture you should Understand that a wave is a means of transferring energy by means of an oscillation or vibration Have a qualitative and quantitative understanding of what a periodic function is Understand what is meant by transverse wave and longitudinal wave Understand what is meant by a mechanical wave and meant by an electromagnetic wave Be able to give examples of some physical quantities which propagate as waves Be able to give one mathematical expression for a wave traveling in one dimension Be able to define the terms wavelength, period, frequency, crest, trough, amplitude and velocity for a wave and be comfortable using the equation v=f Understand what is meant by the phase of a wave and what a phase shift or phase constant is.