Association rules The goal of mining association

Association rules • The goal of mining association rules is to generate all possible rules that exceed some minimum user-specified support and confidence thresholds. • The problem is thus decomposed into two subproblems:

Association rules 1. Generate all items sets that have a support that exceeds the support threshold. These sets are called large or frequent itemsets, because they have large support (not because of their cardinality). 2. For each large itemset, generate all the rules that have a minimum confidence: for a large itemset X and Y X, let Z = X – Y. If support(X)/support(Z) > Confidence threshold, then Z Y. Z Y

Association rules • Generating rules by using large (frequent) itemsets is straightforward. However, if the cardinality of the itemsets is very high, the process becomes very computation-intensive: for m items, the number of distinct itemsets is 2 m (power set). • Basic algorithms for finding association rules try to reduce the combinatorial search space

Association rules: a Basic algorithm 1. Test the support for itemsets of size 1, called 1 itemsets. Discard those that do not meet Minimum Required Support (MRS). 2. Extend the 1 -itemsets by appending one item each time, to generate all candidate 2 -itemsets, test MRS and discard those that do not meet it. 3. Continue until no itemsets can be found. 4. Use itemsets found to generate rules (check confidence).

Association rules • The naive version of this algorithm is a combinatorial nightmare! • Many versions and variants of this algorithm • They use different strategies • Their resulting sets of rules are all the same: Any algorithm for association rules should find the same set of rules although their computational efficiencies and memory requirements may be different. • We will see the Apriori Algorithm

Association rules: The Apriori Algorithm • The key idea: The apriori property: any subsets of a frequent itemset are also frequent itemsets x ABC AB Begin with itemsets of size 1 A ABD x AC B AD x x ACD x BC C x BCD BD x CD D

Stage 1. The Apriori Algorithm: Generating large itemsets • Find large (frequent, i. e. , that meet MRS) itemsets of size 1: F 1 • From k = 2 – Ck = candidates of size k: those itemsets of size k that could be frequent, given Fk-1 – Fk = those itemsets that are actually large, Fk Ck. They meet MRS

Example T TID Minimum support allowed = 50% itemset: count 1. scan T C 1: {a}: 2, {b}: 3, {c}: 3, {d}: 1, {e}: 3 F 1: {a, b}, {a, c}, {a, e}, {b, c}, {b, e}, {c, e} 1 a, c, d 2 b, c, e 3 a, b, c, e 4 b, e {a}: 2, {b}: 3, {c}: 3, {e}: 3 C 2: Items Sets with d are discarded 2. scan T C 2: {a, b}: 1, {a, c}: 2, {a, e}: 1, {b, c}: 2, {b, e}: 3, {c, e}: 2 F 2: {a, c}: 2, {b, e}: 3, {c, e}: 2 C 3: {b, c, e} It is the only candidate because all its subsets are large! 3. scan T C 3: {b, c, e}: 2 F 3: {b, c, e}: 2

Stage 1. The Apriori Algorithm: Generating large (frequent) itemsets Algorithm Apriori(T, minsup) //T Set of n transactions //minsup = minimum support allowed C 1 get. C 1(T); //Get 1 -itemsets and their counts F 1 {f | f C 1, f. count / n minsup}; //Check support FOR (k = 2; Fk-1 ; k++) DO Ck candidate_gen(Fk-1); //Get k-itemsets using Fk-1 FOR each transaction t T DO FOR each candidate c Ck DO IF c is contained in t THEN /*Get counts of the k-itemsets*/ c. count++; END FOR Fk {c Ck | c. count / n minsup} //Check support END FOR RETURN F k Fk; //Union of all Fk (k >1 for rules)

Stage 2: The Apriori Algorithm: generating rules from large itemsets • Note that frequent itemsets association rules • One more step is needed to generate association rules: • For each frequent itemset X: - For each subset A X, A . Let B = X – A Minconf = Minimum - A B is an association rule if confidence(A B) ≥ minconf, i. e. , if (support(A B)/support(A)) ≥ minconf.

Example • Suppose {b, c, e} is a large (frequent) itemset with support 50% • Consider subsets of {b, c, e} and their support: {b, c} = 50% {b, e} = 75%, {c, e} = 50%, {b} = 75%, {c} = 75%, {e} = 75%

Example This subset generates the following association rules: • • • {b, c} {e} {b, e} {c} {c, e} {b} {c, e} {c} {b, e} {e} {b, c} confidence = 50/50 = 100% confidence = 50/75 = 66. 6% All rules have support 50% = support({b, c, e})

Hash-based improvement to A-Priori • During pass 1 of A-Priori (Get 1 -itemsets), most memory is idle • Use that memory to keep counts of buckets into which pairs of items are hashed • Gives extra condition that candidate pairs must satisfy when getting 2 -itemsets (pass 2)

Hash-based improvement to A-Priori • The memory is divided like this: – Space to count each item (Get 1 -itemsets) – Use the rest of the space for the described hashing process • PCY algorithm (Park, Chen, and Yu). It is also known as DHP: direct hashing and pruning

PCY Algorithm Pass 1: FOR each transaction t in T DO FOR each item in t DO add 1 to item’s count get. C 1 END FOR each pair of items in t DO Hash the pair to a bucket and add 1 to the Hashing process count for that bucket END FOR

PCY Algorithm Pass 2: • Count all pairs {i, j} that satisfy the conditions: – Both i and j (taken individually!) are frequent items – The pair {i, j} hashes to a bucket whose count the support s (i. e. , a frequent bucket) • These two conditions are necessary for the pair to have a chance of being frequent.

PCY Example • • • Support s = 3 Items: milk (1), Coke (2), bread (3), Pepsi (4), juice (5). Transactions are t 1 = {1, 2, 3} milk, Coke, bread t 2 = {1, 4, 5} t 3 = {1, 3} t 4 = {2, 5} t 5 = {1, 3, 4} t 6 = {1, 2, 3, 5} t 7 = {2, 3, 5} t 8 = {2, 3}

PCY Example • Hashing a pair {i, j} to a bucket k, where k = hash(i, j) = (i + j) mode 5. That is, for pairs: • (1, 4) and (2, 3) k = 0 • (1, 5) and (2, 4) k = 1 • (2, 5) and (3, 4) k = 2 • (1, 2) and (3, 5) k = 3 • (1, 3) and (4, 5) k = 4

PCY Example • Pass 1: • Item’s count: Item Count 1 5 2 5 3 6 4 2 5 4 • Note that Item 4 does not exceed the support.

PCY Example • • • For each pair in each transaction: t 1 = (1, 2)3 (2, 3)0 (1, 3)4 t 2 = (1, 4)0 (1, 5)1 (4, 5)4 t 3 = (1, 3)4 t 4 = (2, 5)2 t 5 = (1, 3)4 (3, 4)2 (1, 4)0 t 6 = (1, 2)3 (1, 3)4 (1, 5)1 (2, 3)0 (2, 5)2 (3, 5)3 t 7 = (2, 3)0 (2, 5)2 (3, 5)3 t 8 = (2, 3)0 Total: 21 pairs

PCY Example • The hash table is Bucket Count 0 1 2 3 4 6 2 4 4 5 • Bucket 1 does not exceed the support, i. e. , (1, 5) and (2, 4) are not frequent.

PCY Example • Pass 2: • Frequent items are {1, 2, 3, 5} • From the frequent items the candidate pairs are (1, 2) (1, 3) (1, 5) (2, 3) (2, 5) (3, 5) • Candidate (1, 5) is discarded because bucket 1 is not frequent! Discarded by PCY!

Counts of the “surviving” pairs PCY Example Pair (1, 2) (1, 3) (2, 5) (3, 5) Count 2 4 4 3 2 • Note that pairs (1, 2) and (3, 5) does not exceed the support. • Frequent itemsets are {1} {2} {3} {5} {1, 3} {2, 5}

Association rules Other improvements: • Parallel: PCY has been extended into a parallel data mining algorithm. • Transaction reduction: the idea is to get rid of transactions (avoid them in future scans) that do not contain any frequent k-itemsets. • Partition and Parallel: each thread works in a data block. • Sampling: risks inaccurate results, data skew

Association rules • Association rules among hierarchies: it is possible to divide items among disjoint hierarchies, e. g. , foods in a supermarket. • It could be interesting to find associations rules across hierarchies. They may occur among item groupings at different levels. • Consider the following example. Levels of a hierarchy

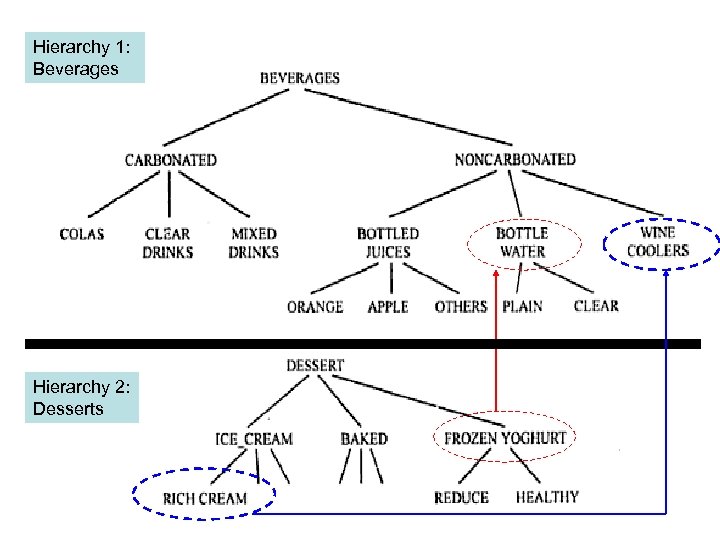Hierarchy 1: Beverages Hierarchy 2: Desserts

Association rules • Associations such as {Frozen Yoghurt} {Bottled Water} {Rich Cream} {Wine Coolers} May produce enough confidence and support to be valid rules of interest.

Association rules: Negative associations • Negative associations: a negative association is of the following type “ 80% of customers who buy W do not buy Z” • The problem of discovering negative associations is complex: there are millions of item combinations that do not appear in the database, the problem is to find only interesting negative rules.

Association rules: Negative associations • One approach is to use hierarchies. Consider the following example: Soft drinks Positive association Joke Wakeup Topsy Chips Days Nightos Parties

Association rules: Negative associations • Suppose a strong positive association between chips and soft drinks • If we find a large support for the fact that when customers buy Days chips they predominantly buy Topsy drinks (and not Joke, and not Wakeup), that would be interesting • The discover of negative associations remains a challenge

Association rules Additional considerations for associations rules: • For very large datasets, efficiency for discovering rules can be improved by sampling Danger: discovering some false rules • Transactions show variability according to geographical location and seasons • Quality of data is usually also variable