53c5caf473e5a7f7839117d3e3c9b2da.ppt
- Количество слайдов: 17
 Association Rule Mining from Weighted Items Muhammad Sulaiman Khan -
Association Rule Mining from Weighted Items Muhammad Sulaiman Khan -
 Weighted ARM l Standard ARM assumes all items have the same significance. For example rules: A: [computer monitor, 5%, 80%], B: [printer scanner, 13%, 80%] In standard ARM rule B is more significant than rule A (rule B has higher support than rule A). In weighted ARM rule A may be more important than rule B, even though the former holds a lower support. This is because, in the above example, rule B items usually carry more profit per unit of sale (standard ARM ignores this).
Weighted ARM l Standard ARM assumes all items have the same significance. For example rules: A: [computer monitor, 5%, 80%], B: [printer scanner, 13%, 80%] In standard ARM rule B is more significant than rule A (rule B has higher support than rule A). In weighted ARM rule A may be more important than rule B, even though the former holds a lower support. This is because, in the above example, rule B items usually carry more profit per unit of sale (standard ARM ignores this).
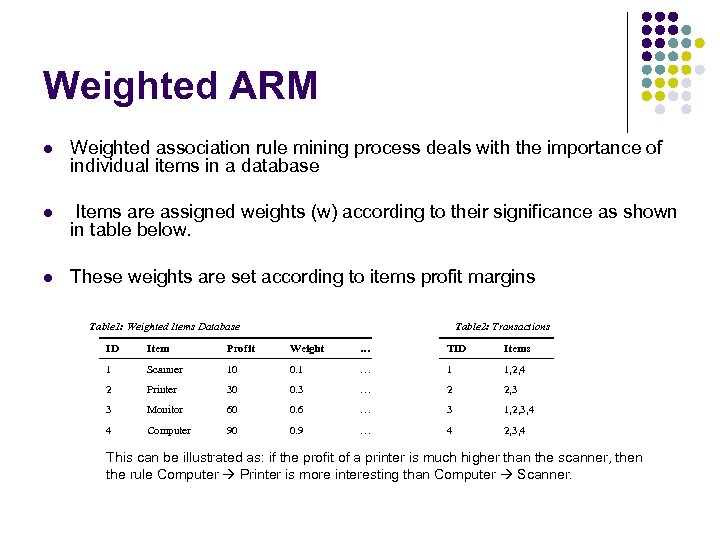 Weighted ARM l Weighted association rule mining process deals with the importance of individual items in a database l Items are assigned weights (w) according to their significance as shown in table below. l These weights are set according to items profit margins Table 1: Weighted Items Database Table 2: Transactions ID Item Profit Weight … TID Items 1 Scanner 10 0. 1 … 1 1, 2, 4 2 Printer 30 0. 3 … 2 2, 3 3 Monitor 60 0. 6 … 3 1, 2, 3, 4 4 Computer 90 0. 9 … 4 2, 3, 4 This can be illustrated as: if the profit of a printer is much higher than the scanner, then the rule Computer Printer is more interesting than Computer Scanner.
Weighted ARM l Weighted association rule mining process deals with the importance of individual items in a database l Items are assigned weights (w) according to their significance as shown in table below. l These weights are set according to items profit margins Table 1: Weighted Items Database Table 2: Transactions ID Item Profit Weight … TID Items 1 Scanner 10 0. 1 … 1 1, 2, 4 2 Printer 30 0. 3 … 2 2, 3 3 Monitor 60 0. 6 … 3 1, 2, 3, 4 4 Computer 90 0. 9 … 4 2, 3, 4 This can be illustrated as: if the profit of a printer is much higher than the scanner, then the rule Computer Printer is more interesting than Computer Scanner.
 Weighted Support & Confidence Support of an itemset X UY is determined by the equation And confidence of rule X Y is the probability that Y exist given that a transaction contains X From table 1 & 2 Computer Printer
Weighted Support & Confidence Support of an itemset X UY is determined by the equation And confidence of rule X Y is the probability that Y exist given that a transaction contains X From table 1 & 2 Computer Printer
 Categorisation of Established WARM Post Processing: where all frequent sets are generated using any classical ARM algorithm and later aggregated weights of itemsets are multiplies with their supports in order to find the weighted support. Pre Processing: In pre processing weighted support is calculated after each step/database scan using the same formula used in post processing. The only obvious reason for pre processing seems to be early pruning and avoid un-necessary generation of frequent sets.
Categorisation of Established WARM Post Processing: where all frequent sets are generated using any classical ARM algorithm and later aggregated weights of itemsets are multiplies with their supports in order to find the weighted support. Pre Processing: In pre processing weighted support is calculated after each step/database scan using the same formula used in post processing. The only obvious reason for pre processing seems to be early pruning and avoid un-necessary generation of frequent sets.
 WARM Issues l With classical Weighted ARM, many potential itemsets are not considered (considering their weights) during the mining step because the only items considered for weighted support are the already generated frequent sets using classical ARM (itemset pool). l Itemsets are first generated using their occurrences in the database and later their weights are considered for weighted support. This approach leads to loose many potential itemsets which could be important if their weights are considered instead of occurrence. l After calculating weighted support, the weighted frequent sets do not hold DCP. l Exhaustive search (Naïve approach) is not possible with high number of items due to computational limitation.
WARM Issues l With classical Weighted ARM, many potential itemsets are not considered (considering their weights) during the mining step because the only items considered for weighted support are the already generated frequent sets using classical ARM (itemset pool). l Itemsets are first generated using their occurrences in the database and later their weights are considered for weighted support. This approach leads to loose many potential itemsets which could be important if their weights are considered instead of occurrence. l After calculating weighted support, the weighted frequent sets do not hold DCP. l Exhaustive search (Naïve approach) is not possible with high number of items due to computational limitation.
 Problem Definition
Problem Definition
 Problem Definition l Item Weight IW is a non-negative real value given to each item ij ranging [0. . 1] with some degree of importance, a weight ij[w]. l Itemset Transaction Weight ITW is the aggregated weights (using some aggregation operator) of all the items in the itemset present in a single transaction. Itemset transaction weight for an itemset X can calculated as:
Problem Definition l Item Weight IW is a non-negative real value given to each item ij ranging [0. . 1] with some degree of importance, a weight ij[w]. l Itemset Transaction Weight ITW is the aggregated weights (using some aggregation operator) of all the items in the itemset present in a single transaction. Itemset transaction weight for an itemset X can calculated as:
 Problem Definition Boolean weighted support is calculated as: Boolean weighted confidence is calculated as:
Problem Definition Boolean weighted support is calculated as: Boolean weighted confidence is calculated as:
 Weighted Support & Confidence framework Fuzzy weighted support is calculated as: Fuzzy weighted confidence is calculated as:
Weighted Support & Confidence framework Fuzzy weighted support is calculated as: Fuzzy weighted confidence is calculated as:
 Fuzzy Weighted ARM Technique l WARM issues present in previous approaches have been addressed. l Proposed Fuzzy Weighted Support & Confidence framework (FWARM) deals with binary and fuzzy quantitative attributes. l In the framework both quantitative and qualitative properties of attributed have been considered in rules generation process. l Frequent itemsets generated using the proposed approach maintains the DCP. l Publications: [ICDM’ 08, ALSIP’ 08(PAKDD), Book Chapter “Rare Association Rule Mining and Knowledge Discovery: Technologies for Infrequent and Critical Event Detection”
Fuzzy Weighted ARM Technique l WARM issues present in previous approaches have been addressed. l Proposed Fuzzy Weighted Support & Confidence framework (FWARM) deals with binary and fuzzy quantitative attributes. l In the framework both quantitative and qualitative properties of attributed have been considered in rules generation process. l Frequent itemsets generated using the proposed approach maintains the DCP. l Publications: [ICDM’ 08, ALSIP’ 08(PAKDD), Book Chapter “Rare Association Rule Mining and Knowledge Discovery: Technologies for Infrequent and Critical Event Detection”
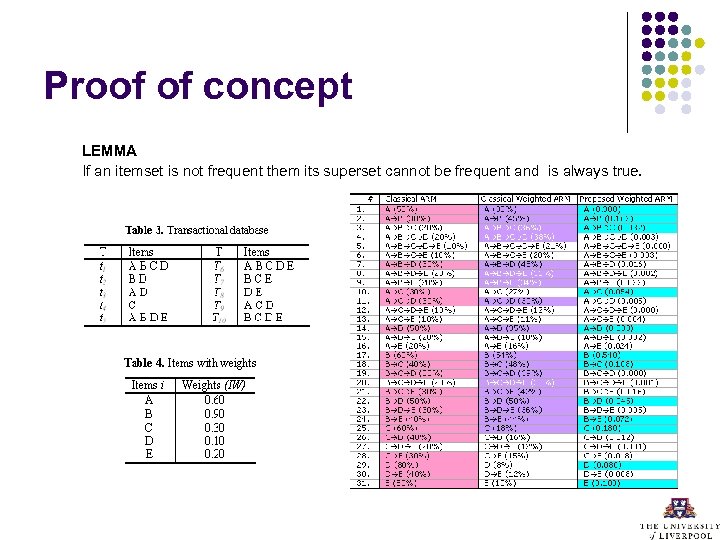 Proof of concept LEMMA If an itemset is not frequent them its superset cannot be frequent and is always true.
Proof of concept LEMMA If an itemset is not frequent them its superset cannot be frequent and is always true.
 FWARM Algorithm
FWARM Algorithm
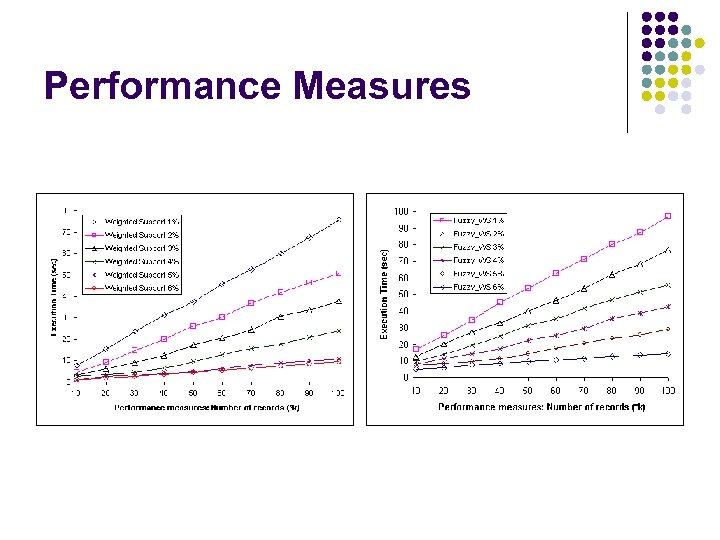
 Experimental Results The data is a transactional database containing 100 K records and 1 K items. Two sets of experiments were undertaken: l First experiment show that the output behaviour of our proposed framework is quite similar to classical ARM because we use the Apriori approach in our algorithm but results are better than WARM. Experiments show l (i) the number of frequent sets generated (using weighted support measure) and l (ii) the number of rules generated (using weighted confidence measure) l Experiment two shows comparison of execution times using different weighted supports and data sizes.
Experimental Results The data is a transactional database containing 100 K records and 1 K items. Two sets of experiments were undertaken: l First experiment show that the output behaviour of our proposed framework is quite similar to classical ARM because we use the Apriori approach in our algorithm but results are better than WARM. Experiments show l (i) the number of frequent sets generated (using weighted support measure) and l (ii) the number of rules generated (using weighted confidence measure) l Experiment two shows comparison of execution times using different weighted supports and data sizes.
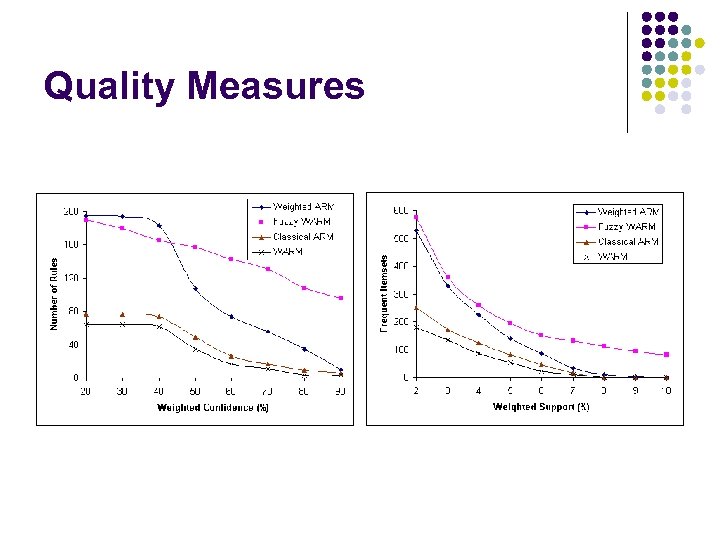 Quality Measures
Quality Measures
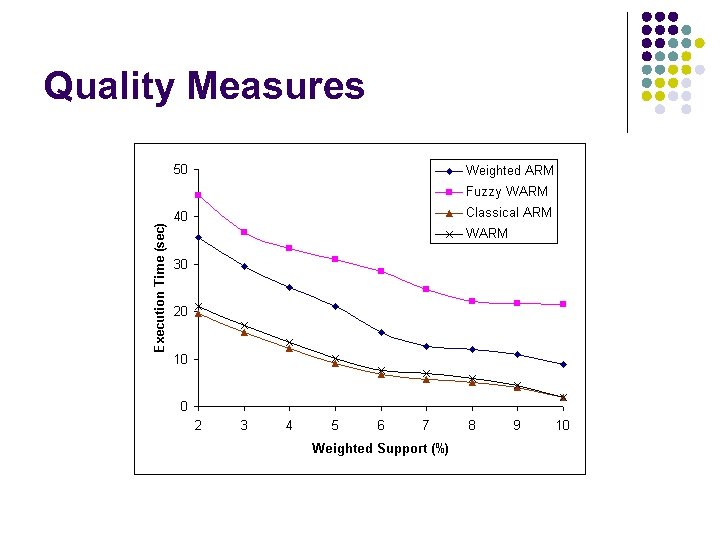 Quality Measures
Quality Measures
 Performance Measures
Performance Measures


