481afdc6a34d164a0dbab31a024c7efd.ppt
- Количество слайдов: 73

Assembly Language for Intel-Based Computers, 5 th Edition Kip R. Irvine Chapter 17: Floating-Point Processing and Instruction Encoding Slide show prepared by the author Revision date: June 4, 2006 (c) Pearson Education, 2006 -2007. All rights reserved. You may modify and copy this slide show for your personal use, or for use in the classroom, as long as this copyright statement, the author's name, and the title are not changed.

Chapter Overview • Floating-Point Binary Representation • Floating-Point Unit Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 2

Floating-Point Binary Representation • IEEE Floating-Point Binary Reals • Finite precision numbers used to approximate real numbers • Normalized Binary Floating-Point Numbers • Creating the IEEE Representation • Converting Decimal Fractions to Binary Reals Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 3

Representing a Real Number • Sign • 1 = negative, 0 = positive • Significand (or mantissa) • decimal digits to the left & right of decimal point • weighted positional notation • Example: 123. 154 = (1 x 102) + (2 x 101) + (3 x 100) + (1 x 10– 1) + (5 x 10– 2) + (4 x 10– 3) • Exponent • integer Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 4

IEEE Floating-Point Binary Reals • Types • Single Precision 32 bits: 1 bit for the sign, 8 bits for the exponent, and 23 bits for the fractional part of the significand. • Double Precision 64 bits: 1 bit for the sign, 11 bits for the exponent, and 52 bits for the fractional part of the significand. • Extended Precision 80 bits: 1 bit for the sign, 16 bits for the exponent, and 63 bits for the fractional part of the significand. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 5

Floating Point Representations • We can write N in terms of fraction f (0 ≤ f < 1) N = (− 1)s x (1 + f ) x 2 e • The IEEE-754 single and double precision formats: 8 bits s 23 bits Exponent Fraction Single Precision (32 bits) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. 11 bits s 52 bits Exponent Fraction Double Precision (64 bits) Web site Examples 6

Normalizing Binary Floating-Point Numbers • Mantissa is normalized when a single 1 appears to the left of the binary point • Unnormalized: shift binary point until exponent is zero • Examples • The 1 in 1 + f (= 1. f ) is not stored explicitly, it is implied! Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 7

Representation for the Exponent • n The exponent e uses a biased representation. an unsigned number E is stored in the exponent field such that e = E − 011… 1 b. • e = E − 1023 for double-precision (0 ≤ E < 2048) • e = E − 127 for single-precision (0 ≤ E < 256) Examples: What will be the value in the exponent field for 1. 1. 27 = 1. 27 X 20, so exponent e = 0. Hence, E = e + 127 = 7 Fh is stored in the exponent field 2. 12. 0 = 1. 100 … x 23, So, e = 3. Hence, E = e + 127 = 130 = 82 h is stored in the exponent field 3. 0. 25 = 1. 0 x 2− 2 So, e =− 2. Hence, E = e + 127 = 127 − 2 = 125 = 7 Dh Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 8
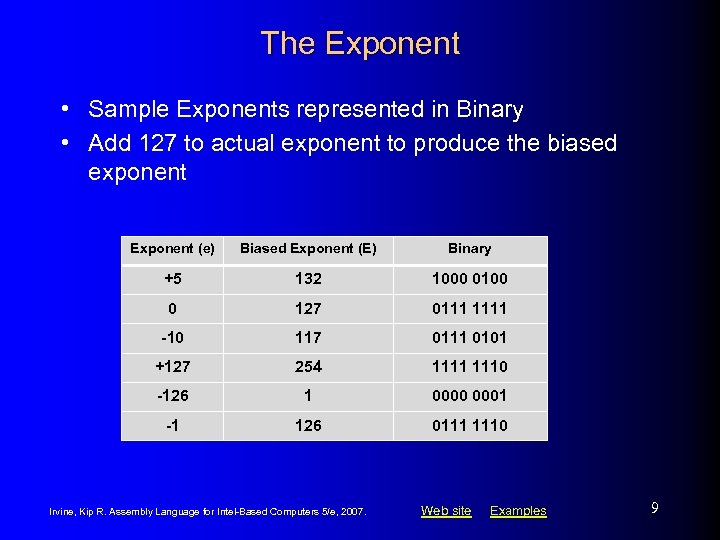
The Exponent • Sample Exponents represented in Binary • Add 127 to actual exponent to produce the biased exponent Exponent (e) Biased Exponent (E) Binary +5 132 1000 0100 0 127 0111 1111 -10 117 0111 0101 +127 254 1111 1110 -126 1 0000 0001 -1 126 0111 1110 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 9
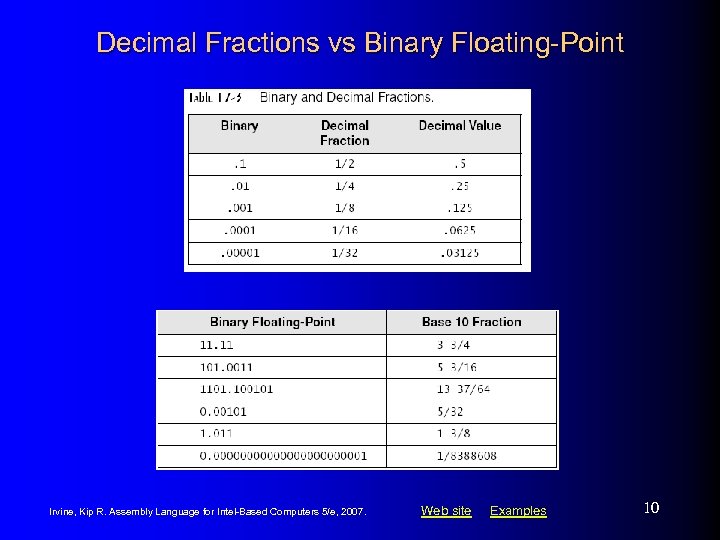
Decimal Fractions vs Binary Floating-Point Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 10

Converting Fractions to Binary Reals • Express as a sum of fractions having denominators that are powers of 2 • Examples Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 11

Representation of the Fraction • In base-2, any fraction f < 1 can be written as f = b− 1 x 2− 1 +b− 2 x 2− 2 +. . . = (b− 1, b− 2, b− 3, …) Where each bi Є 0, 1 is a bit and b− 1 is the MSB of the fraction • The algorithm to find each bit of a fraction f (ex. f =. 6) 1. The MSB of the fraction is 1 iff f ≥ 1/2. Hence the MSB = 1 iff 2 f ≥ 1 2. Let f ' be the fraction part of 2 f. Then the next MSB of f is 1 iff 2 f ' ≥ 1 3. Let f '' be the fraction part of 2 f '. Then the next MSB of f is 1 iff 2 f '' ≥ 1 4. . and so on Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 12

Representation for the Fraction (cont) • Example. find all bits of f = 0. 15 2 x 0. 30 2 x 0. 60 2 x 0. 20 2 x 0. 40 2 x 0. 80 2 x 0. 60 = 0. 30 MSB = 0. 60 0 = 1. 20 1 = 0. 40 0 = 0. 80 0 = 1. 60 1 repeat of last 4 bits Hence 0. 15 = 0. 001001 b = 0. 0010011001. . . b. When truncation is used, the following 23 bits will be stored in the single precision fraction field: 001001100110011 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 13
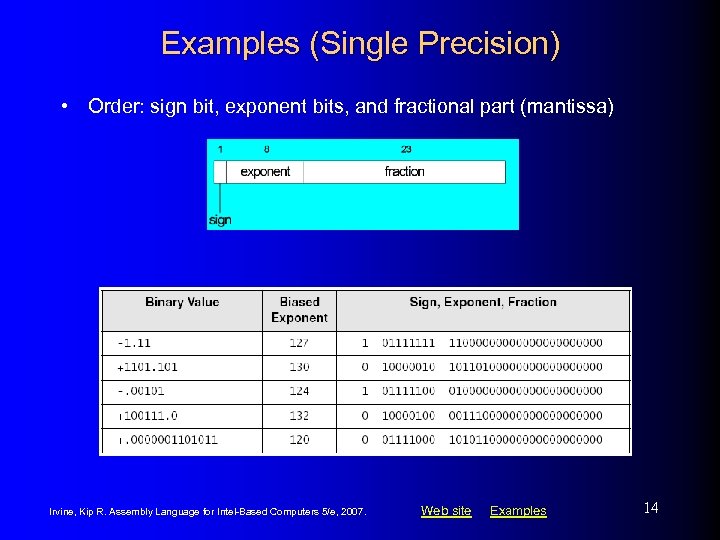
Examples (Single Precision) • Order: sign bit, exponent bits, and fractional part (mantissa) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 14

Your Turn … Find the IEEE single-precision representation, in hexadecimal, of the following decimal numbers (assume that truncation is used for rounding) 1) 1. 0 = 0 01111111 0000 … 0 = 3 F 800000 2) 0. 5 = 0 01111110 0000 … 0 = 3 F 000000 3) − 83. 7 = - 0101 0011. 10110 = - 1. 010011 10110 x 26 1 10000101 01001110110 … 0110 = C 2 A 76666 4) 1. 1 E− 55 Underflow: cannot be represented usingle precision Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 15

Converting Single-Precision to Decimal 1. If the MSB is 1, the number is negative; otherwise, it is positive. 2. The next 8 bits represent the exponent. Subtract binary 01111111 (decimal 127), producing the unbiased exponent. Convert the unbiased exponent to decimal. 3. The next 23 bits represent the significand – an implied “ 1. ”, followed by the significand bits. Trailing zeros can be ignored. Create a floating-point binary number, using the significand, the sign determined in step 1, and the exponent calculated in step 2. 4. Un-normalize the binary number produced in step 3. (Shift the binary point the number of places equal to the value of the exponent. Shift right if the exponent is positive, or left if the exponent is negative. ) 5. From left to right, use weighted positional notation to form the decimal sum of the powers of 2 represented by the floating-point binary number. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 16

Example Convert 0 10000010 01011000000000 to Decimal 1. The number is positive. 2. The biased exponent is E = 130 3. The unbiased exponent is binary 00000011, or 3 decimal 4. Combining the sign, exponent, and significand, the binary number is +1. 01011 X 23. 5. The unnormalized binary number is +1010. 11. 6. The decimal value is +10 3/4, or +10. 75. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 17

Your Turn … Give the decimal value represented by the IEEE single-precision representation given below in hexadecimal 1. 45 AC 0000 h = 0 1000101100 … 0 = 1. 01011 X 212 = 101011 X 27 = 43 X 128 = 5504 2. C 4800000 h = 1 10001001 0000000 … 0 = -1. 00. . 0 X 210 = - 1. 0 X 210 = -1024 3. 3 FE 00000 h = 0 01111111 1100000 … 0 = 1. 11 X 20 = 1. 75 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 18

Rounding • Most real numbers cannot be represented exactly with a finite number of bits • Many rational numbers (like 1/3 or 17. 15) cannot be represented exactly in an IEEE format • Rounding refers to the way in which a real number will be approximated by another number that belongs to a given format Ex: if a format uses only 3 decimal digits to represent a fraction, should 2/3 be represented as 0. 666 or 0. 667? Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 19

Rounding (cont) • Truncation is only one of the methods used for rounding. Three other methods are supported by IEEE 1. Round to the nearest number (default IEEE) 2. Round towards +∞ 3. Round towards −∞ 4. Round towards 0 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 20

Recap of Floating Point Representation N = (− 1)s x (1 + f ) x 2 e • exponent e uses a biased representation. It is represented by unsigned integer E such that e = E − 0111 … 1 b • Let F be the unsigned integer obtained by concatenating the bits of the fractions f • Hence, a floating point number N is represented by (s, E, F) and the “ 1” is implied (not represented) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 21

Representing Specific Values • Problem 1: we have no representation of zero!! • The IEEE standard specifies that zero is represented by E = F = 0 • Because of the sign-bit, we have both a positive and a negative zero Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 22

Representing Specific Values • Problem 2: Only a few bits are allocated to E. So, numbers with very large (and very small) magnitudes cannot be represented • The IEEE standard has reserved the following interpretation when E contains only ones 1. +∞ when s = 0; E = 111 : : : 1 and F = 0 2. −∞ when s = 1; E = 111 : : : 1 and F = 0 3. Not a number (Na. N) when E = 111 : : : 1, F ≠ 0 Hence, normal floating point values exist only for E < 111 … 11 • The +−∞ value arises only when a computation gives a number that would require E > 111 … 11 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 23

Representing Specific Values • The +−∞ value can be used in operands with predictable results 1. +∞ + N = +∞ 2. −∞ + N = −∞ 3. +∞ ++∞ = +∞ • Undefined values are represented by Na. N 1. +∞ +−∞ = Na. N 2. +−∞ / +−∞ = Na. N 3. 0/0 = Na. N Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 24

Real-Number Encodings • • • Normalized finite numbers • all the nonzero finite values that can be encoded in a normalized real number between zero and infinity Positive and Negative Infinity Na. N (not a number) • bit pattern that is not a valid FP value • Two types: quiet signaling • Specific encodings (single precision): Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 25

Denormalized Numbers • The smallest non-zero magnitude is: • E = 0 and F = 00 … 01. This gives a value of : • 1. 00 … 01 x 2− 127 in single-precision • To allow smaller magnitudes to be represented, IEEE introduced denormalized numbers • A denormalized number has E = 0 and F != 0. The implicit ” 1” to the left of ”. ” now becomes ” 0” Therefore, the smallest non-zero single-precision denormalized number is: 0. 00 … 01 x 2− 127 = 2− 23 x 2− 127 = 2− 150 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 26

Denormalized Numbers (cont) The largest single-precision denormalized number is: 2− 127 x (1 − 2− 23) • normalized numbers use E such that 0 < E < 11 … 1 The smallest (positive) single-precision normalized number is then: 1. 00 … 0 x 2− 126 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 27

What's Next • Floating-Point Binary Representation • Floating-Point Unit Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 28

Floating Point Unit • • FPU Register Stack Floating-Point Instruction Set Arithmetic Instructions Comparing Floating-Point Values Reading and Writing Floating-Point Values Floating-Point Exceptions Mixed-Mode Arithmetic Masking and Unmasking Exceptions Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 29

General Purpose FPU Registers • There are 8 general-purpose FPU registers; each 80 bit wide Single-precision or double-precision values of the IEEE-754 standard are placed within those 80 bits in an extended format • They are organized as a stack maintained by the FPU • The current top of the stack is referred by ST(Stack Top) or ST(0). ST(1) is the register just below ST, and ST(n) is the n-th register below ST • 15 bits are reserved for the exponent: e = E − 3 FFFh Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 30

FPU Register Stack • Eight individually addressable 80 bit registers: R 0 - R 7. • 64 -bit mantissa, 15 -bit exponent, 1 sign-bit • The “ 1” in the mantissa is stored explictly • Three-bit field named TOP in the FPU status word identifies the register number that is currently the top of stack. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 31

Special-Purpose Registers • Opcode register: stores opcode of last non- control instruction executed • Control register: controls precision and rounding method for calculations • Status register: top-of-stack pointer, condition codes, exception warnings • Tag register: indicates content type of each register in the register stack • Last instruction pointer register: pointer to last non-control executed instruction • Last data (operand) pointer register: points to data operand used by last executed instruction Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 32

The Tag Register • The Tag register is a 16 -bit register 1. The first 2 bits, called Tag(0), specify the type of data contained in ST(0) 2. Tag(i ) specifies the type of data contained in ST(i ) for i = 0; … ; 7 3. The 2 -bit value of Tag(i ) indicates the following about the content of ST(i ) 00 : ST(i ) contains a valid number 01 : ST(i ) contains zero 10 : ST(i ) contains Na. N or ∞ 11 : ST(i ) is empty Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 33

Directives and Instructions • Use REAL 4 directive to allocate 32 bits of storage for a floating point number and store a value according to the IEEE-754 standard Sp. Nb REAL 4 1. 0 ; Sp. Nb = 3 F 80000 h • Use REAL 8 directive to allocate 64 bits of storage and store a IEEE double-precision value Dp. Nb REAL 8 1. 0 ; Dp. Nb = 3 FF 0000000 h • Use the REAL 10 directive to allocate 80 bits (ten bytes) of storage and store a floating point number according to intel’s 80 -bit extended precision format Ep. Nb REAL 10 1. 0 ; Ep. Nb = 3 FFF 800000000 h Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 34

Defining Floating Point Values in ASM • We can use the REAL 4 directive to define a singleprecision floating point value Float 1 REAL 4 17. 15 ; single-precision float Float 2 REAL 4 1. 715 E+1 ; same value as above • We can use the REAL 8 directive to define a double precision floating point value Double 1 REAL 8 0. 001235 ; double-precision float Double 1 REAL 8 1. 235 E-3 ; same value as above Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 35

FPU Instruction Set • Instruction mnemonics begin with letter F • Second letter identifies data type of memory operand • B = bcd • I = integer • no letter: floating point • Examples • FBLD • FIST • FMUL load binary coded decimal store integer multiply floating-point operands Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 36

FPU Instruction Set • Operands • • zero, one, or two no immediate operands no general-purpose registers (EAX, EBX, . . . ) integers must be loaded from memory onto the stack and converted to floating-point before being used in calculations • if an instruction has two operands, one must be a FPU register Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 37

Data Transfer Instructions • FLD Source Transfers data from a Mem source into ST • Source can either be a double-word, a quad-word or a tenbyte memory operand or ST(i), but NOT a CPU register. • The data is converted from the IEEE format to Intel’s extended-precision format during the data transfer to ST. data • The FPU stack after loading A and B X REAL 8 4. 78 E-7 ST(0) Y Y REAL 10 85. 6 E+8 ST(1) X. code ST(2) ST(3) FLD X ST(4) FLD Y ST(5) ST(6) ST(7) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 38

Data Transfer Instructions (cont) • Example: If we execute FLD ST(1) instruction (with the initial stack as shown), we get the following FPU stack ST(0) Y ST(0) X ST(1) Y ST(2) X ST(3) ST(4) ST(5) ST(6) ST(7) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 39

Data Transfer Instructions (cont) • FST Destination: copies floating point operand from the top of the FPU stack into memory or ST(i). • FSTP Destination copies ST onto destination and pops ST. ST(0) FLD X FLD Y FLD Z FSTP Result FINIT ; clears the stack Z ST(1) Y ST(2) X ST(0) Y ST(1) X Before FSTP Result After FSTP Result ST(2) ST(0) After FINIT ST(1) ST(2) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 40

Data Transfer Instructions (cont) • The CPU and FPU are executing concurrently • normally cannot transfer data between CPU registers and FPU registers directly. • When FPU transfers data onto memory that is to be used by CPU, we should instruct the CPU to wait until FPU completes the data transfer. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Example: . data Float 1 REAL 4 1. 75 Result DWORD ? . code FINIT FLD Float 1 FADD Float 1 FIST Result FWAIT MOV EAX, Result Web site Examples 41

Floating-Point I/O • Irvine 32 library procedures • Read. Float reads FP value from keyboard, pushes it on the FPU stack • Write. Float writes value from ST(0) to the console window in exponential format • Show. FPUStack displays contents of FPU stack Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 42

Floating Point Input Output • The following two library functions are provided for input and output of floating point numbers. • Read. Float: Reads a floating point value entered by the user and places it on ST (0) • Write. Float: Outputs the value on ST(0) as a floating point number • Example: . data fval 1 REAL 4 ? fval 2 REAL 4 5. 67. code call Read. Float ; places user entered value on ST fst fval 1 ; fval 1 is assigned value just entered by user fld fval 2 ; 5. 67 is placed on ST call Write. Float ; 5. 67 is output on the screen Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 43

FXCH Instruction • FXCH swaps the content of two registers. It can be used either with zero or one operand 1. If no operand is used, FXCH operates on the contents of ST and ST(1) 2. If an operand is used, then it must be ST(n), FXCH swaps the content of ST and ST(n) ST(0) FLD X FLD Y FLD Z FXCH ST(2) Z ST(1) Y ST(2) X Before EXCH ST(2) ST(0) X ST(1) Y ST(2) Z After EXCH ST(2) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 44

IEEE Format Conversion • We can convert from one format to another simply by pushing onto and popping from the FPU stack. data ADouble REAL 8 -7. 77 E-6 AFloat REAL 4 ? ; double-precision value ; single-precision value . code FLD ADouble FSTP AFloat ; double to extended-precision ; extended to single-precision Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 45

Integer Floating Point Conversion • FILD Source converts a Source integer into floating point value. data X DWORD 5. code FILD X ; stores 5. 0 on ST(0) • FIST Destination converts a floating point value into a Destination integer. data X REAL 4 5. 64 Y DWORD ? . code FLD X ; stores 5. 64 on ST(0) FIST Y ; stores 6 in variable Y Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 46

Arithmetic Instructions • Can have up to two operands as long as one of them is a FPU register • CPU registers are not allowed as operands • A memory operand can be 32 or 64 bits • Mem-to-Mem operations are not allowed • Several addressing modes are provided. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 47
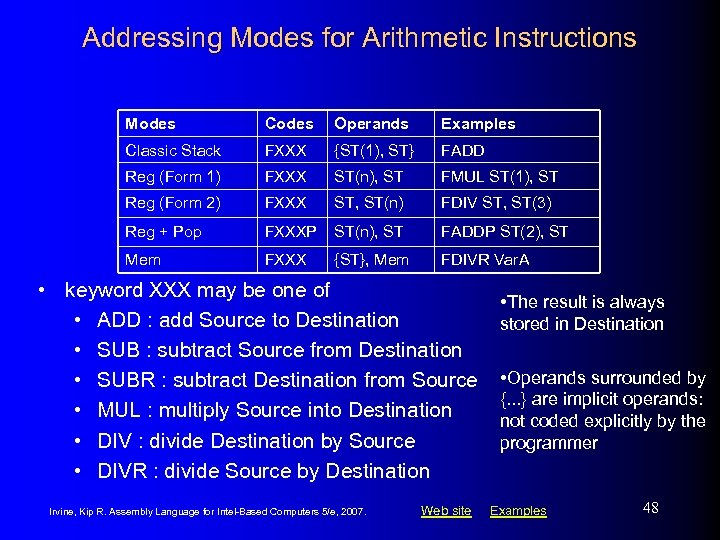
Addressing Modes for Arithmetic Instructions Modes Codes Operands Examples Classic Stack FXXX {ST(1), ST} FADD Reg (Form 1) FXXX ST(n), ST FMUL ST(1), ST Reg (Form 2) FXXX ST, ST(n) FDIV ST, ST(3) Reg + Pop FXXXP ST(n), ST FADDP ST(2), ST Mem FXXX {ST}, Mem FDIVR Var. A • keyword XXX may be one of • ADD : add Source to Destination • SUB : subtract Source from Destination • SUBR : subtract Destination from Source • MUL : multiply Source into Destination • DIV : divide Destination by Source • DIVR : divide Source by Destination Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site • The result is always stored in Destination • Operands surrounded by {. . . } are implicit operands: not coded explicitly by the programmer Examples 48

Classic Stack Addressing Mode • The classical stack addressing mode is invoked when we use FXXX without operands 1. ST is the implied Source 2. ST(1) is the implied Destination 3. The result of the instruction is temporarily stored into ST(1) and then the stack is popped. Hence, ST will then contain the result. Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 49

Classic Stack Addressing Mode FLD X FLD Y FLD Z FSUB ST(0) Z ST(0) Y - Z ST(1) Y ST(1) X ST(2) After FSUB Before FSUB • Note: ST(0) would contain Z – Y if FSUBR was used instead Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 50

Register Addressing Mode • Uses explicitly two registers as operands where one of them must be ST 1. ST can either be Source or Destination operand, so two forms are permitted ST, ST(n) or ST(n), ST 2. In fact, both operands can be ST • The stack is not popped after the operation FLD X ST(0) FLD Y ST(1) ST(2) FLD Z FMUL ST(2), ST Z ST(0) Z Y ST(1) Y X ST(2) X*Z Before FMUL Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. After FMUL Web site Examples 51

Register + Pop Addressing Mode • Uses explicitly two registers as operands 1. Source must be ST and Destination must be ST(n) where n must be different from 0 2. The result of the operation is first stored into ST(n) and then the stack is popped [so the result is then in ST(n - 1)] FLD X FLD Y ST(0) FLD Z ST(1) ST(2) FMULP ST(2), ST Z ST(0) Y Y ST(1) X*Z X ST(2) Before FMUL Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. After FMUL Web site Examples 52

Memory Addressing Mode • ST is an implicit destination operand • Source is a memory operand • The following program computes the area of a circle . data Pi REAL 4 3. 14159 Radius REAL 4 2. 0 Area REAL 4 ? . code main PROC FLD PI ; ST(1) = Pi FLD Radius FMUL Radius ; mem addressing ; ST = Radius x Radius FMUL ; ST = Area FSTP Area FWAIT exit main ENDP Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 53

Arithmetic with an Integer • The memory addressing mode also supports an integer for its explicit operand. But the arithmetic instruction must now be FIXXX (like FIMUL, FIADD, FIDIV, . . . ). data Five DWORD 5 My. Fp REAL 4 3. 3 Area REAL 4 ? . code main: FLD My. Fp ; ST = 3. 3 FIMUL Five ; ST = 16. 5 FIADD Five ; ST = 21. 5 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. ; an integer ; a floating point Web site Examples 54

Mixed-Mode Arithmetic • Combining integers and reals. • Integer arithmetic instructions such as ADD and MUL cannot handle reals • FPU has instructions that promote integers to reals and load the values onto the floating point stack. • Example: Z = N + X. data N SDWORD 20 X REAL 8 3. 5 Z REAL 8 ? . code fild N fwait fadd X fstp Z ; load integer into ST(0) ; wait for exceptions ; add mem to ST(0) ; store ST(0) to mem Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 55

Your Turn … • 1. 2. 3. 4. 5. 6. Suppose that we have the following FPU stack content before each instruction below: ST(0) = 0. 6, ST(1) = 1. 2, ST(2) = 1. 8 and the rest of the FPU stack is empty. Give the stack content after the execution of each instruction: FSTP Result ; ST=1. 2, ST(1)=1. 8 FDIVR ST(2), ST ; ST=0. 6, ST(1)=1. 2, ST(2)=0. 3333 FMUL ; ST=0. 72, ST(1)=1. 8 FSUBRP ST(1), ST ; ST=-0. 6, ST(1)=1. 8 FADD ; ST=1. 8, ST(1)=1. 8 FDIVP ST(1), ST ; ST= 2. 0, ST(1)=1. 8 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 56

The FPU Status Word Register 15 14 C 3 • 13 11 10 Stack Top C 2 8 C 1 C 0 7 6 5 PE UE 0 0 E ZE DE IE The FPU Status Word (SW) register contains 1. Exception flags (bits 0 to 5) that signals division by zero, overflow, underflow, stack-overflow and stack-underflow, . . . 2. A Stack Top pointer that indicates which register is the top of the stack 3. Four condition bits: C 0, C 1, C 2 and C 3 that are set by certain instruction like FCOM, FTST and FXAM • Each has a corresponding mask bit • if set when an exception occurs, the exception is handled automatically by FPU • if clear when an exception occurs, a software exception handler is invoked 57 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples

Exception Flags IE (Invalid Error) signals stack-overflow/underflow, a Na. N result, or the use of Na. N as an operand. The FPU generates Na. N if that exception is masked DE (Denormalized Operand Error) the FPU accepts the operand if that exception is masked ZE (Zero Error) attempt to divide by zero. The FPU generates ∞ if that exception is masked Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 58

Exception Flags OE (Overflow Error) signals a result too large to be stored in the destination operand. The FPU generates exception is masked ∞ if that UE (Underflow Error) signals a non-zero result too small to be stored in the destination operand. The FPU generates zero if that exception is masked PE (Precision Error) signals a result that exceeds the selected precision Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 59

Masking and Unmasking Exceptions • Exceptions masked by default (handled automatically by CPU) • E. g. divide by zero just generates infinity, without halting the program • If you unmask an exception • processor executes an appropriate exception handler • Bits 0 to 5 are used to mask exception flags in the FPU Status Word register 1. FSTCW Destination : copies the Control. Word (CW) register into Destination 2. FLDCW Source : load Source into the CW register 15 12 11 10 RC 9 8 7 PC Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. 6 5 PM 0 UM Web site OM ZM Examples DM IM 60

The Control Word Register 15 12 11 10 9 RC • 8 7 6 PC 5 0 PM UM OM ZM DM IM Example: mask all exceptions without affecting the other bits of the CW register . data Excpt. code FSTCW FWAIT OR FLDCW WORD ? Excpt ; copy CW into Excpt, 111111 b ; sets to 1 bits 0 to 5 Excpt ; masks all exceptions Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 61

Your turn … • Unmask the divide by zero exception : . data ctrl. Word WORD ? . code fstcw ctrl. Word ; get the control word fwait and ctrl. Word, 1111111011 b ; unmask divide by zero fldcw ctrl. Word ; load it back into FPU 15 12 11 RC 10 9 8 7 6 PC Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. 5 PM 0 UM Web site OM ZM Examples DM IM 62

The Control Word Register (cont) 15 12 11 RC 10 9 8 7 6 PC 5 0 PM UM OM ZM DM IM • RC (Rounding Control) 00 = Round to nearest 01 = Round toward minus infinity 10 = Round toward plus infinity 11 = Truncate toward zero • PC (Precision Control) 00 = Single-precision 01 = Reserved (i. e. not defined) 10 = Double-precision 11 = Extended-precision (on 80 bits) [default] Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 63

Comparing FP Values • FCOM instruction • Operands: Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 64

FCOM • Condition codes set by FPU: codes similar to CPU flags 15 14 C 3 13 11 10 Stack Top C 2 8 C 1 7 C 0 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. 6 5 PE UE Web site 0 0 E ZE Examples DE IE 65
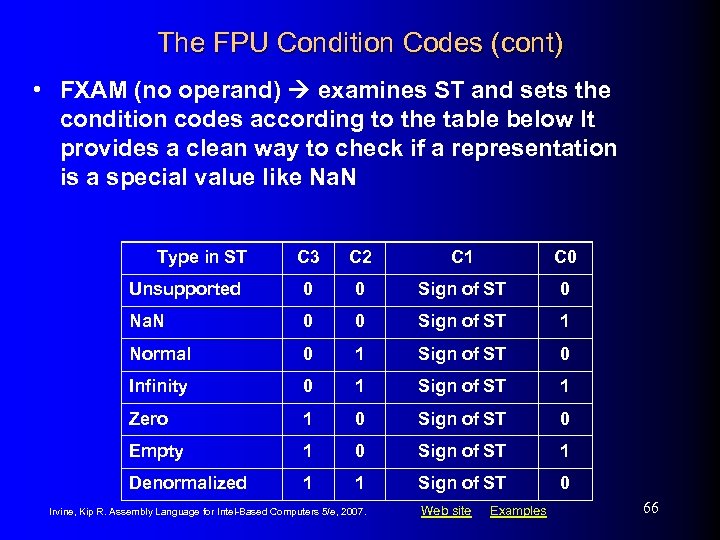
The FPU Condition Codes (cont) • FXAM (no operand) examines ST and sets the condition codes according to the table below It provides a clean way to check if a representation is a special value like Na. N Type in ST C 3 C 2 C 1 C 0 Unsupported 0 0 Sign of ST 0 Na. N 0 0 Sign of ST 1 Normal 0 1 Sign of ST 0 Infinity 0 1 Sign of ST 1 Zero 1 0 Sign of ST 0 Empty 1 0 Sign of ST 1 Denormalized 1 1 Sign of ST 0 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 66

The FPU Condition Codes (cont) • FSTSW AX transfers the FPU SW into AX. We can the test the content of AX with CPU instructions, in order to perform a decision based on the settings of the FPU condition codes • FSTSW AX is the only instruction that provides direct communication between the FPU and CPU via a general purpose CPU register Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 67

Branching after FCOM • Required steps: 1. Use the FSTSW instruction to move the FPU status word into AX. 2. Use the SAHF instruction to copy AH into the EFLAGS register. 3. Use JA, JB, etc to do the branching. Fortunately, the FCOMI instruction does steps 1 and 2 for you. fcomi ST(0), ST(1) jnb Label 1 Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 68

Comparing for Equality • Calculate the absolute value of the difference between two floating-point values. data epsilon REAL 8 1. 0 E-12 val 2 REAL 8 0. 0 val 3 REAL 8 1. 001 E-13 ; very small value ; value to compare . code ; if( val 2 == val 3 ), display "Values are equal". fld epsilon fld val 2 fsub val 3 fabs fcomi ST(0), ST(1) ja skip m. Write <"Values are equal", 0 dh, 0 ah> skip: Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 69

Comparing for Equality • Calculate the absolute value of the difference between two floating-point values. data epsilon REAL 8 1. 0 E-12 val 1 REAL 4 2. 0 ; very small value ; value to compare . code fld epsilon fld val 1 fsqrt fmul ST(0), ST(0) fsub val 1 ; result should be 0, actually ST(0) = 4. 4408921 E-16 fabs fcomi ST(0), ST(1) ja skip m. Write <"Values are equal", 0 dh, 0 ah> skip: Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 70

Other FPU Operations • These instructions use ST as an implicit operand store the result back into ST Instructions Description FABS Convert ST to positive FCHS Change the sign of ST FSQRT Compute sqrt of ST FSIN Compute sine of ST FCOS Compute cosine of ST • Example: finding the roots of a quadratic equation using Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 71

Other FPU Operations (cont) • These instructions push a constant onto ST Instructions Constant FLDZ +0: 0 FLD 1 +1: 0 FLDPI Pi FLDL 2 T log 2(10) FLDL 2 E log 2(e) FLDLG 2 log 10(2) FLDLN 2 loge(2) Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 72

FPU Code Example expression: . data val. A REAL 8 val. B REAL 8 val. C REAL 8 val. D REAL 8. code fld val. A fchs fld val. B fmul val. C fadd fstp val. D = –val. A + (val. B * val. C). 1. 5 2. 5 3. 0 ? ; will be +6. 0 ; ; ; ST(0) = val. A change sign of ST(0) load val. B into ST(0) *= val. C ST(0) += ST(1) store ST(0) to val. D Irvine, Kip R. Assembly Language for Intel-Based Computers 5/e, 2007. Web site Examples 73
481afdc6a34d164a0dbab31a024c7efd.ppt