АСИММЕТРИЧНАЯ МЕТОДОЛОГИЯ 10 СИСТЕМА ДИФФИ-ХЕЛЛМАНА Система

АСИММЕТРИЧНАЯ МЕТОДОЛОГИЯ § 10. СИСТЕМА ДИФФИ-ХЕЛЛМАНА

Система Диффи-Хеллмана Алгоритм Диффи — Хеллмана — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный канал связи. Был впервые опубликован в 1976 году. Алгоритм основан на трудности вычислений дискретных логарифмов. Алгоритм не может быть использован, когда в сети возможно несанкционированное изменение данных ( «человек посередине» ).

1. Абоненты обмениваются несекретно некоторыми двумя числами p (простое число, порядка 10300) и g (примитивный корень – небольшое). 2. Абоненты генерируют большие случайные числа: первый абонент — число a, второй абонент — число b (а и b порядка 10100). 3. Первый абонент вычисляет значение A = gamod p и пересылает его второму, а второй вычисляет B = gbmod p и передаёт первому. 4. Первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение Bamod p = gabmod p, а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение Abmod p = gabmod p. 5. У обоих абонентов получилось одно и то же число: K = gabmod p секретный ключ. 6. Вычисление gabmod p по перехваченным gamod p и gbmod p, если числа p, a, b выбраны достаточно Первый абонент Второй абонент большими – неразрешимо за приемлемое время.

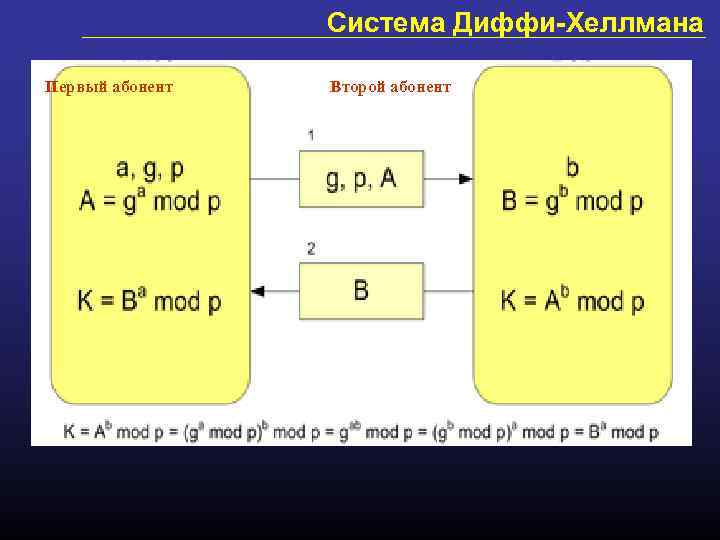Система Диффи-Хеллмана Первый абонент Второй абонент

Система Диффи-Хеллмана Пример работы алгоритма Диффи-Хеллмана: 1. Пусть p = 47, а примитивный корень g = 23. 2. Предположим, что абоненты выбрали свои секретные ключи: a =12 и b = 33. 3. Абоненты вычисляют значения частных открытых ключей: A = gamod p=2312 mod 47 = 27, B = gbmod p = 2333 mod 47 = 33. 4. После обмена открытыми A и B, абоненты вычисляют общий секретный ключ: первый абонент Ba mod p = 3312 mod 47=25 второй абонент Ab mod p = 2733 mod 47=25 Секретный ключ K = g ab mod p = 2312*33 = 23396 mod 47 = 25 K = 25