Artificial Neural Networks Rados Jovanovic Summary

Artificial Neural Networks Rados Jovanovic

Summary • • • Biological Model of Neural Networks Mathematical Model of Neural Networks Building an Artificial Neural Network Theoretical Properties Applications of Artificial Neural Networks

Biological Model • The brain is responsible for all processing and memory. • The brain consists of a complex network of cells called neurons. • Neurons communicate by transimitting electrochemical signals throughout the network. • Each input signal to a neuron can inhibit or excite the neuron. When the neuron is excited enough, it will fire its own electrochemical signal.

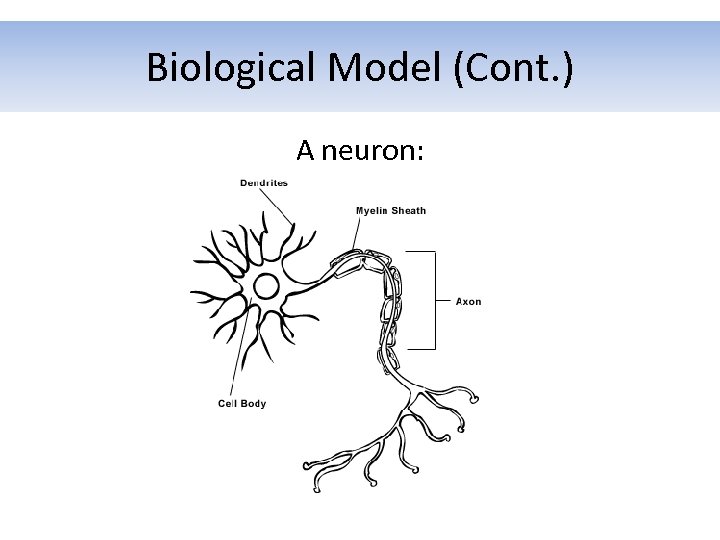Biological Model (Cont. ) A neuron:

Mathematical Model • An Artificial Neural Network is a network of interconnected artificial neurons. • Like in a biological neural network, artificial neurons communicate by sending signals to one another. • Each input to an artificial neuron can either inhibit or excite the artificial neuron.

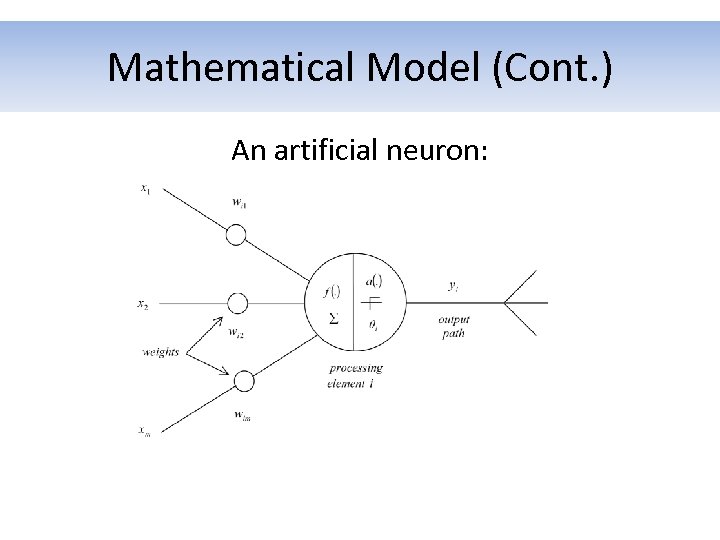Mathematical Model (Cont. ) An artificial neuron:

Building an Artificial Neural Network • Topology of the network • Learning type • Learning algorithm – Backpropagation • Summary of backpropagation

Topology of the Network (Cont. ) There are many topologies, but the main distinction can be maid between: • Feed-Forward Neural Networks • Recurrent Neural Networks

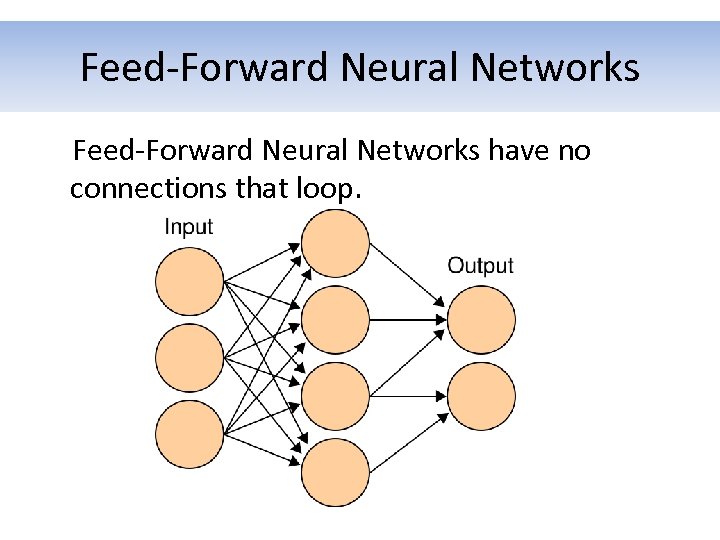Feed-Forward Neural Networks have no connections that loop.

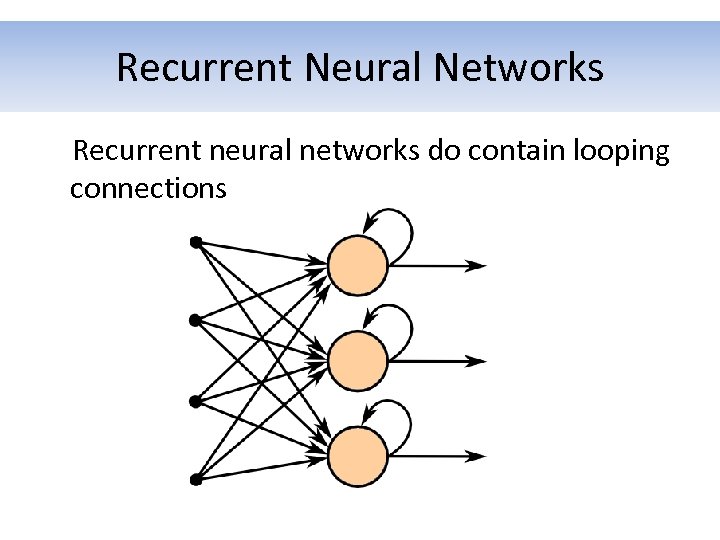Recurrent Neural Networks Recurrent neural networks do contain looping connections

Building an Artificial Neural Network • Topology of the network • Learning type • Learning algorithm – Backpropagation • Summary of backpropagation

Learning Type • Supervised Learning Requires a set of pairs of inputs and outputs to train the artificial neural network on. • Unsupervised Learning Only requires inputs. Through time an ANN learns to organize and cluster data by itself. • Reinforcement Learning An ANN from the given input produces some output, and the ANN is rewarded or punished based on the output it created.

Building an Artificial Neural Network • Topology of the network • Learning type • Learning algorithm – Backpropagation • Summary of backpropagation

Learning Algorithm Learning is adjustment of the weights of the connections between neurons, according to some modification rule.

Backpropagation • One of the more common algorithms for supervised learning is Backpropagation. • The term is an abbreviation for “backwards propagation of errors" • Backpropagation is most useful for feedforward networks.

Backpropagation (Cont. ) • An input is fed into the network and the output is being calculated. • We compare the output of the network with the target output, and we get the error. • We want to minimize the error, so we greedily adjust the weights such that error for this particular input will go towards zero. • We do so using the delta rule.

Delta Rule • The delta rule is a gradient descent learning rule. • For a given neuron j and a weight i the delta rule for its weight wji is: • • tj is the target output yj is the actual output xi is the ith input a is a small constant called the learning rate

Delta Rule (Cont. )

Delta Rule (Cont. )

Backpropagation (Cont. ) • The whole process is repeated for each of the training cases, then back to the first case again. • The cycle is repeated until the overall error value drops below some pre-determined threshold. • Backpropagation usually allows quick convergence on satisfactory local minima for error.

Summary of Backpropagation -While error over all training samples > threshold -For each training sample: -Present a training sample to the neural network. -Compute the output of the network. -Calculate the error for each neuron in the last layer by comparing it to the target output. -For each layer l starting from the last output layer until the first layer -Adjust the weights for each neuron in layer l to decrease the local error. -Propagate the error to each neuron one layer back -end for

Theoretical Properties • • Computational power Capacity Generalisation Convergence

Theoretical Properties • Computational power: The Cybenko theorem proved single hidden layer, feed forward neural network is capable of approximating any continuous, multivariate function to any desired degree of accuracy.

Theoretical Properties (Cont. ) • Capacity: It roughly corresponds to the neural network’s ability to model any given function. It is related to the amount of information that can be stored in the network.

Theoretical Properties (Cont. ) • Generalisation: In applications where the goal is to create a system that generalises well in unseen examples, the problem of overtraining has emerged. • To lessen the overtraining cross validation is used.

Theoretical Properties (Cont. ) • Convergence: Not much can be said about convergence since it depends on many factors, such as the existence of local minima, choice of optimization method, etc.

Applications Application areas include: system identification and control (vehicle control, process control), quantum chemistry, gameplaying and decision making (backgammon, chess, racing), pattern recognition (radar systems, face identification, object recognition. . . ), sequence recognition (gesture, speech, handwritten text recognition), medical diagnosis, financial applications (automated trading systems), data mining, visualization, e-mail spam filtering. . .

Fin Questions?