Artificial Intelligence AI Planning Sungwook Yoon What

Artificial Intelligence (AI) Planning Sungwook Yoon

What do we (AI researchers) mean by Plan? Sungwook Yoon

plan n. 1. A scheme, program, or method worked out beforehand for the accomplishment of an objective: a plan of attack. 2. A proposed or tentative project or course of action: had no plans for the evening. 4. A drawing or diagram made to scale showing the structure or arrangement of something. 5. In perspective rendering, one of several imaginary planes perpendicular to the line of vision between the viewer and the object being depicted. 3. A systematic arrangement of elements 6. A program or policy stipulating a service or benefit: a pension plan. or important parts; a configuration or outline: a seating plan; the plan of a Synonyms: blueprint, design, project, story. scheme, strategy

plan n. 1. A scheme, program, or method worked out beforehand for the accomplishment of an objective: a plan of attack (or exit).

plan n. 2. A proposed or tentative project or course of action: had no plans for the evening.

plan n. 3. A systematic arrangement of elements or important parts; a configuration or outline: a seating plan; the plan of a story.

plan n. 4. A drawing or diagram made to scale showing the structure or arrangement of something.

plan n. 5. In perspective rendering, one of several imaginary planes perpendicular to the line of vision between the viewer and the object being depicted.

plan n. 6. A program or policy stipulating a service or benefit: a pension plan.

plan n. 1. A scheme, program, or method worked out beforehand for the accomplishment of an objective: a plan of attack. 2. A proposed or tentative project or course of action: had no plans for the evening. 4. A drawing or diagram made to scale showing the structure or arrangement of something. 5. In perspective rendering, one of several imaginary planes perpendicular to the line of vision between the viewer and the object being depicted. 3. A systematic arrangement of elements 6. A program or policy stipulating a service or benefit: a pension plan. or important parts; a configuration or outline: a seating plan; the plan of a Synonyms: blueprint, design, project, story. scheme, strategy

Automated Planning concerns … • Mainly synthesizing a course of actions to achieve the given goal • Finding actions that need to be conducted in each situation – When you are going to Chicago – In Tempe, “take a cab” – In Sky Harbor, “take the plane” • In summary, planning tries to find a plan (course of actions) given the initial state (you are in Tempe) and the goal (you want to be in Chicago) Sungwook Yoon

What is a Planning Problem? • Any problem that needs sequential decision – For a single decision, you should look for Machine Learning • Classification • Given a picture “is this a cat or a dog? ” • Any Examples? – Free. Cell – Sokoban – Micro-mouse – Bridge Game – Football Sungwook Yoon

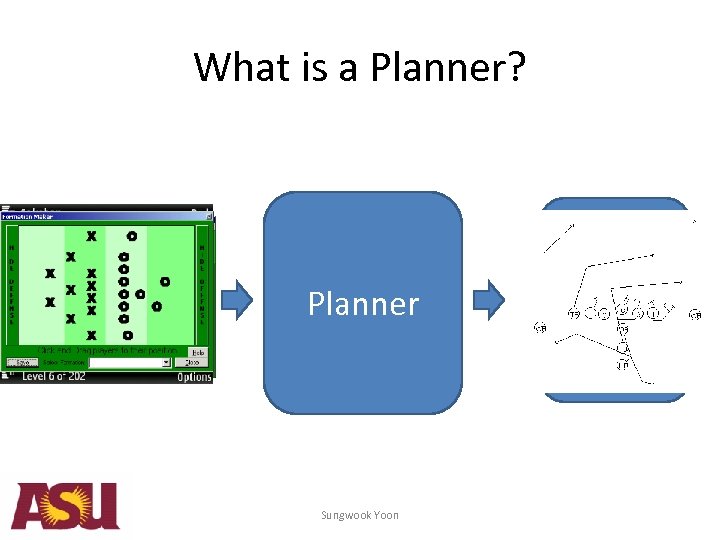What is a Planner? Planner Sungwook Yoon 1. Move spade 2 1. Move block to the cell 1 to left 2. Move space 3 2. Move block to theabove 1 to cell 3. ….

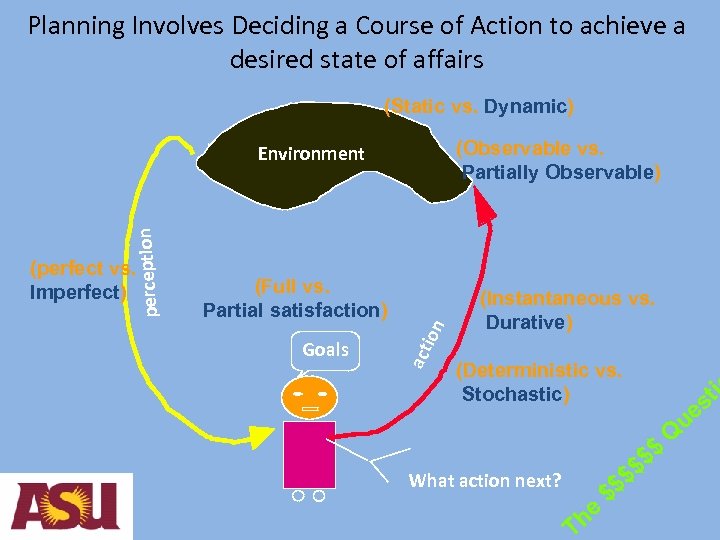Planning Involves Deciding a Course of Action to achieve a desired state of affairs (Static vs. Dynamic) (Observable vs. Partially Observable) (Full vs. Partial satisfaction) Goals ion (perfect vs. Imperfect) act perception Environment (Instantaneous vs. Durative) (Deterministic vs. Stochastic) ti s ue $$ $ What action next? he T $$ $ Q

Any real world application for planning please? Sungwook Yoon

Space Exploration • Autonomous planning, scheduling, control – NASA: JPL and Ames • Remote Agent Experiment (RAX) – Deep Space 1 • Mars Exploration Rover (MER)

Manufacturing • Sheet-metal bending machines - Amada Corporation – Software to plan the sequence of bends [Gupta and Bourne, J. Manufacturing Sci. and Engr. , 1999]

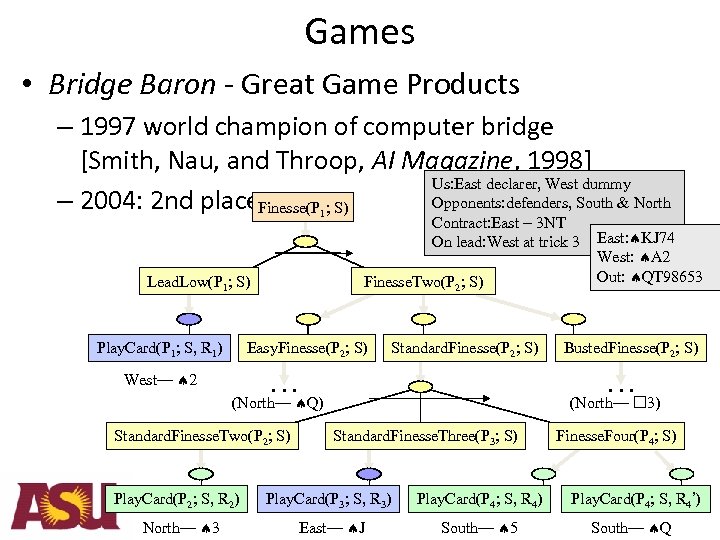Games • Bridge Baron - Great Game Products – 1997 world champion of computer bridge [Smith, Nau, and Throop, AI Magazine, 1998] Us: East declarer, West dummy Opponents: defenders, South & North – 2004: 2 nd place. Finesse(P ; S) 1 Lead. Low(P 1; S) Play. Card(P 1; S, R 1) Contract: East – 3 NT On lead: West at trick 3 Finesse. Two(P 2; S) Easy. Finesse(P 2; S) West— 2 Standard. Finesse(P 2; S) … Play. Card(P 2; S, R 2) North— 3 Busted. Finesse(P 2; S) … (North— Q) Standard. Finesse. Two(P 2; S) East: KJ 74 West: A 2 Out: QT 98653 (North— 3) Standard. Finesse. Three(P 3; S) Finesse. Four(P 4; S) Play. Card(P 3; S, R 3) Play. Card(P 4; S, R 4’) East— J South— 5 South— Q

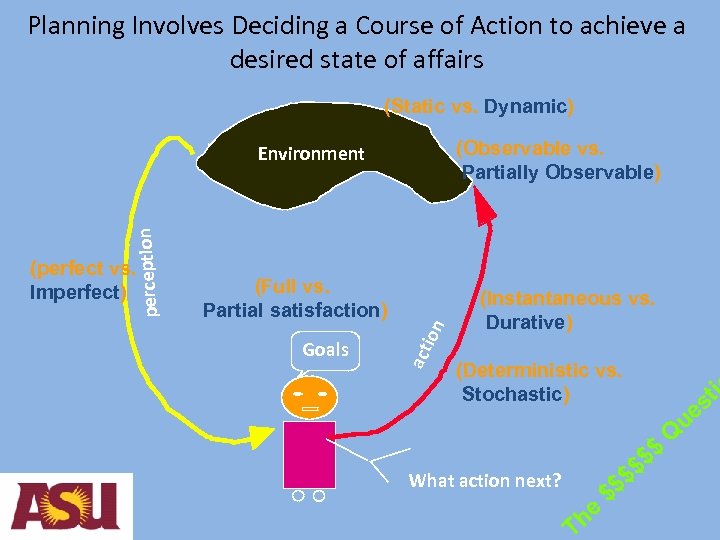Planning Involves Deciding a Course of Action to achieve a desired state of affairs (Static vs. Dynamic) (Observable vs. Partially Observable) (Full vs. Partial satisfaction) Goals ion (perfect vs. Imperfect) act perception Environment (Instantaneous vs. Durative) (Deterministic vs. Stochastic) ti s ue $$ $ What action next? he T $$ $ Q

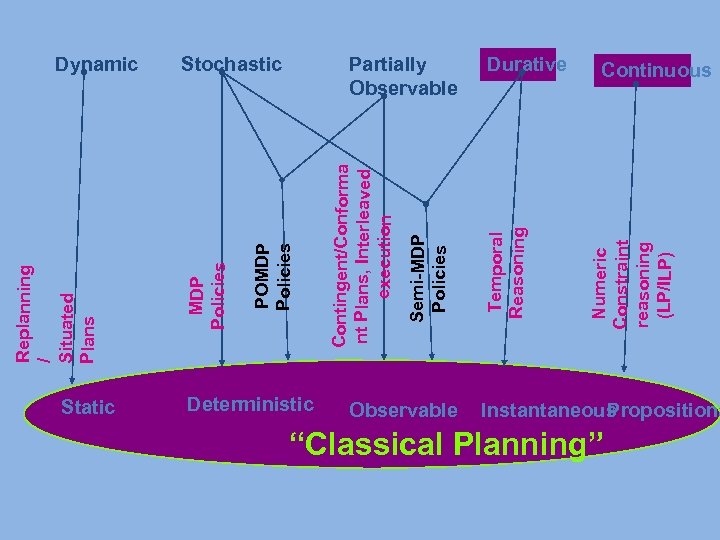Static Deterministic Observable Durative Numeric Constraint reasoning (LP/ILP) Partially Observable Temporal Reasoning Semi-MDP Policies Stochastic Contingent/Conforma nt Plans, Interleaved execution POMDP Policies Replanning / Situated Plans Dynamic Continuous Instantaneous ropositiona P “Classical Planning”

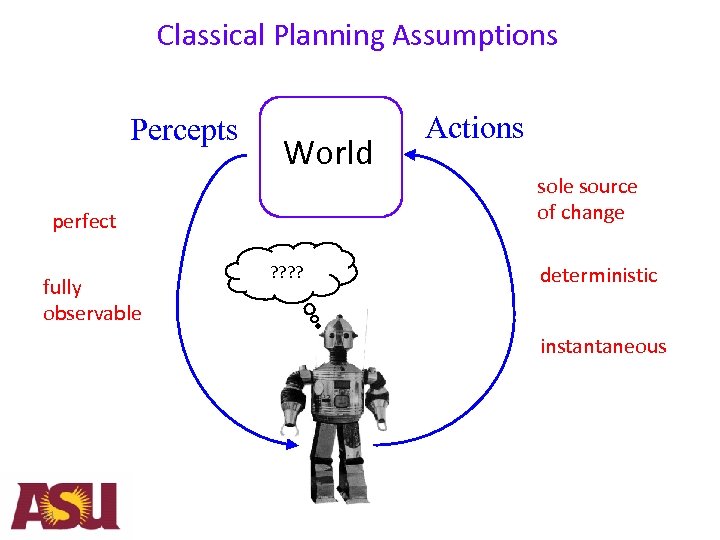Classical Planning Assumptions Percepts World perfect fully observable ? ? Actions sole source of change deterministic instantaneous 21

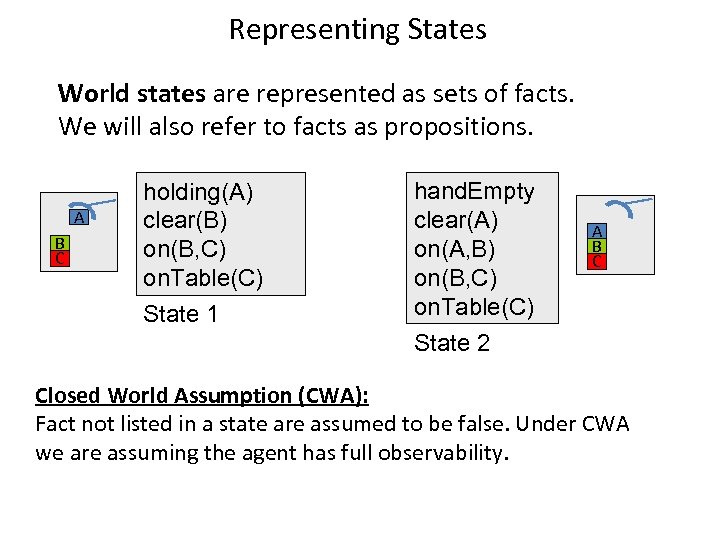Representing States World states are represented as sets of facts. We will also refer to facts as propositions. A B C holding(A) clear(B) on(B, C) on. Table(C) State 1 hand. Empty clear(A) on(A, B) on(B, C) on. Table(C) State 2 A B C Closed World Assumption (CWA): Fact not listed in a state are assumed to be false. Under CWA we are assuming the agent has full observability.

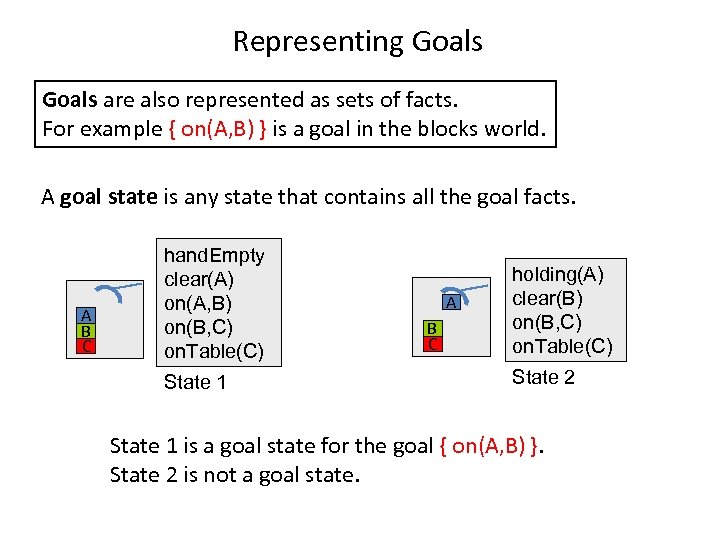Representing Goals are also represented as sets of facts. For example { on(A, B) } is a goal in the blocks world. A goal state is any state that contains all the goal facts. A B C hand. Empty clear(A) on(A, B) on(B, C) on. Table(C) State 1 A B C holding(A) clear(B) on(B, C) on. Table(C) State 2 State 1 is a goal state for the goal { on(A, B) }. State 2 is not a goal state.

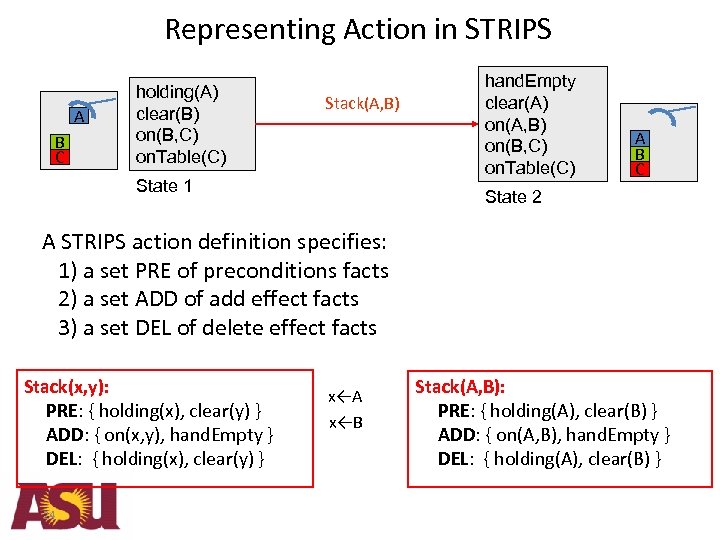Representing Action in STRIPS A B C holding(A) clear(B) on(B, C) on. Table(C) Stack(A, B) State 1 hand. Empty clear(A) on(A, B) on(B, C) on. Table(C) A B C State 2 A STRIPS action definition specifies: 1) a set PRE of preconditions facts 2) a set ADD of add effect facts 3) a set DEL of delete effect facts Stack(x, y): PRE: { holding(x), clear(y) } ADD: { on(x, y), hand. Empty } DEL: { holding(x), clear(y) } 24 x←A x←B Stack(A, B): PRE: { holding(A), clear(B) } ADD: { on(A, B), hand. Empty } DEL: { holding(A), clear(B) }

Semantics of STRIPS Actions A B C holding(A) clear(B) on(B, C) on. Table(C) S Stack(A, B) hand. Empty clear(A) on(A, B) on(B, C) on. Table(C) A B C S ADD – DEL A STRIPS action is applicable (or allowed) in a state when its preconditions are contained in the state. • Taking an action in a state S results in a new state S ADD – DEL (i. e. add the add effects and remove the delete effects) • Stack(A, B): PRE: { holding(A), clear(B) } ADD: { on(A, B), hand. Empty } DEL: { holding(A), clear(B) } 25

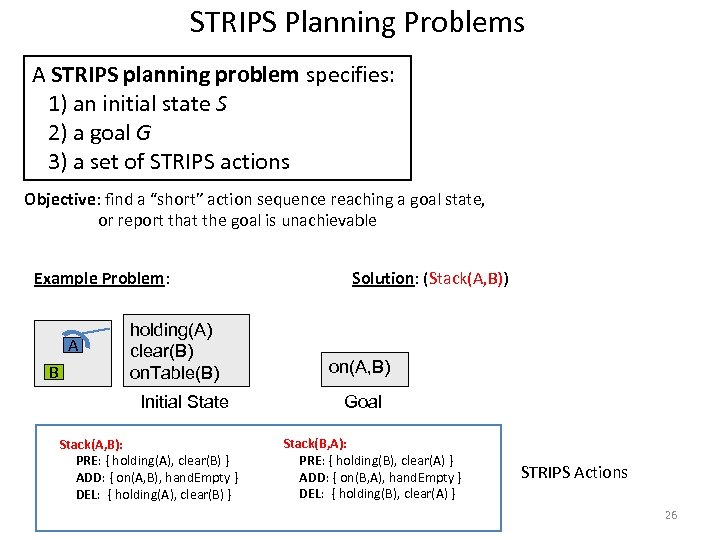STRIPS Planning Problems A STRIPS planning problem specifies: 1) an initial state S 2) a goal G 3) a set of STRIPS actions Objective: find a “short” action sequence reaching a goal state, or report that the goal is unachievable Example Problem: A B holding(A) clear(B) on. Table(B) Initial State Stack(A, B): PRE: { holding(A), clear(B) } ADD: { on(A, B), hand. Empty } DEL: { holding(A), clear(B) } Solution: (Stack(A, B)) on(A, B) Goal Stack(B, A): PRE: { holding(B), clear(A) } ADD: { on(B, A), hand. Empty } DEL: { holding(B), clear(A) } STRIPS Actions 26

Properties of Planners h A planner is sound if any action sequence it returns is a true solution h A planner is complete outputs an action sequence or “no solution” for any input problem h A planner is optimal if it always returns the shortest possible solution Is optimality an important requirement? Is it a reasonable requirement? 27

Complexity of STRIPS Planning Plan. SAT Given: a STRIPS planning problem Output: “yes” if problem is solvable, otherwise “no” h Plan. SAT is decidable. 5 Why? h In general Plan. SAT is PSPACE-complete! Just finding a plan is hard in the worst case. 5 even when actions limited to just 2 preconditions and 2 effects Does this mean that we should give up on AI planning? NOTE: PSPACE is set of all problems that are decidable in polynomial space. PSPACE-complete is believed to be harder than NP-complete 28

Satisficing vs. Optimality h While just finding a plan is hard in the worst case, for many planning domains, finding a plan is easy. h However finding optimal solutions can still be hard in those domains. 5 For example, optimal planning in the blocks world is NP- complete. h In practice it is often sufficient to find “good” solutions “quickly” although they may not be optimal. 5 For example, finding sub-optimal blocks world solutions can be done in linear time. How? ?

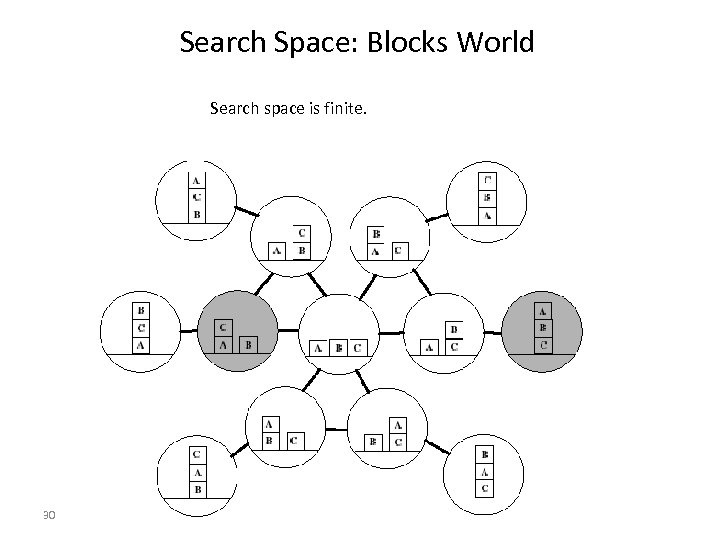Search Space: Blocks World Search space is finite. 30

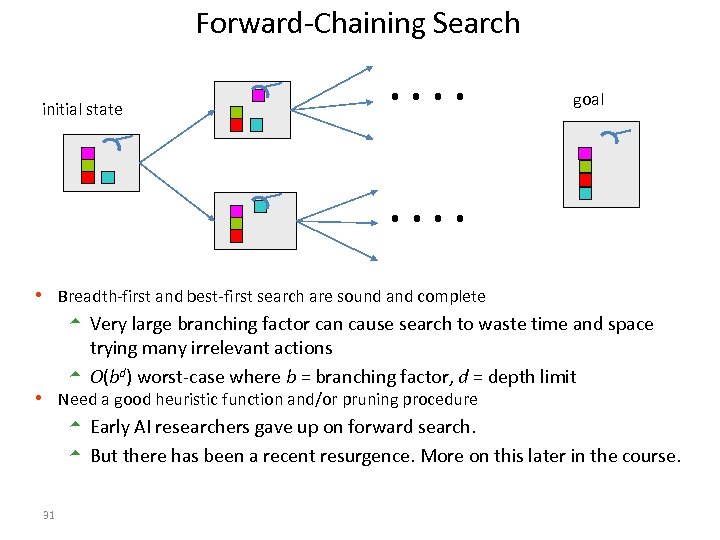Forward-Chaining Search initial state . . goal . . h Breadth-first and best-first search are sound and complete 5 Very large branching factor can cause search to waste time and space trying many irrelevant actions 5 O(bd) worst-case where b = branching factor, d = depth limit h Need a good heuristic function and/or pruning procedure 5 Early AI researchers gave up on forward search. 5 But there has been a recent resurgence. More on this later in the course. 31

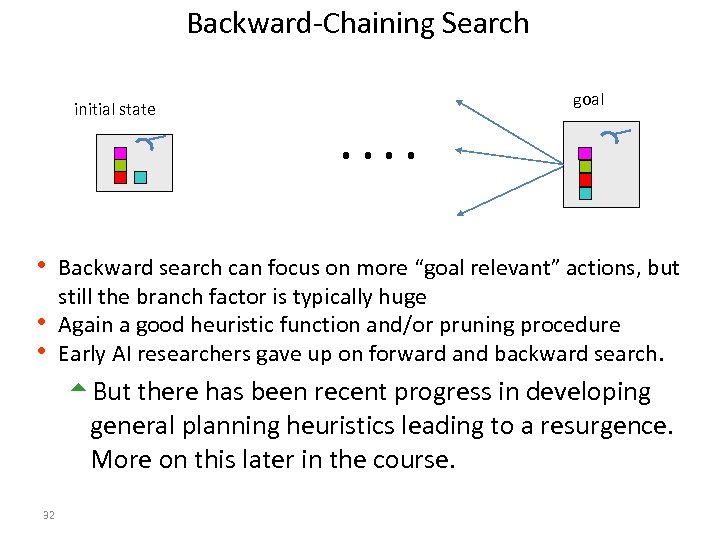Backward-Chaining Search initial state goal . . h Backward search can focus on more “goal relevant” actions, but still the branch factor is typically huge h Again a good heuristic function and/or pruning procedure h Early AI researchers gave up on forward and backward search. 5 But there has been recent progress in developing general planning heuristics leading to a resurgence. More on this later in the course. 32

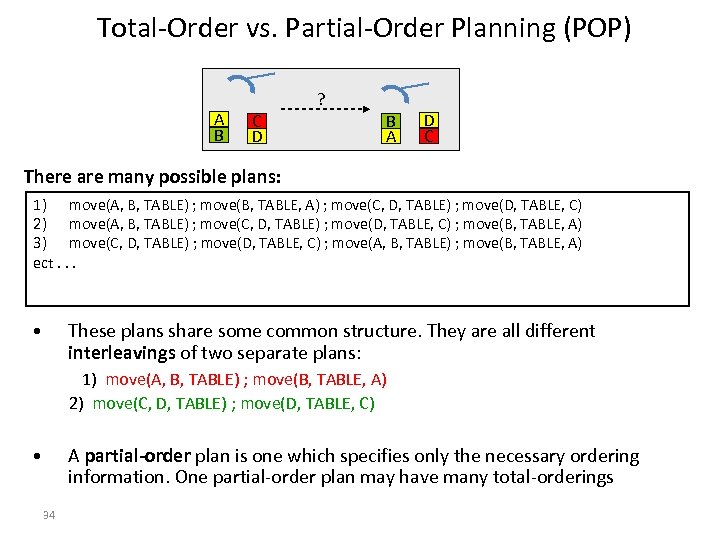
Total-Order vs. Partial-Order Planning (POP) A B ? C D B A D C There are many possible plans: 1) move(A, B, TABLE) ; move(B, TABLE, A) ; move(C, D, TABLE) ; move(D, TABLE, C) 2) move(A, B, TABLE) ; move(C, D, TABLE) ; move(D, TABLE, C) ; move(B, TABLE, A) 3) move(C, D, TABLE) ; move(D, TABLE, C) ; move(A, B, TABLE) ; move(B, TABLE, A) ect. . . h State-space planning techniques produce totally-ordered plans, i. e. plans consisting of a strict sequence of actions. h Often, however, there are many possible orderings of actions than have equivalent effects. h However, often many orderings of the actions have equivalent effects. 33

Total-Order vs. Partial-Order Planning (POP) A B ? C D B A D C There are many possible plans: 1) move(A, B, TABLE) ; move(B, TABLE, A) ; move(C, D, TABLE) ; move(D, TABLE, C) 2) move(A, B, TABLE) ; move(C, D, TABLE) ; move(D, TABLE, C) ; move(B, TABLE, A) 3) move(C, D, TABLE) ; move(D, TABLE, C) ; move(A, B, TABLE) ; move(B, TABLE, A) ect. . . • These plans share some common structure. They are all different interleavings of two separate plans: 1) move(A, B, TABLE) ; move(B, TABLE, A) 2) move(C, D, TABLE) ; move(D, TABLE, C) • A partial-order plan is one which specifies only the necessary ordering information. One partial-order plan may have many total-orderings 34

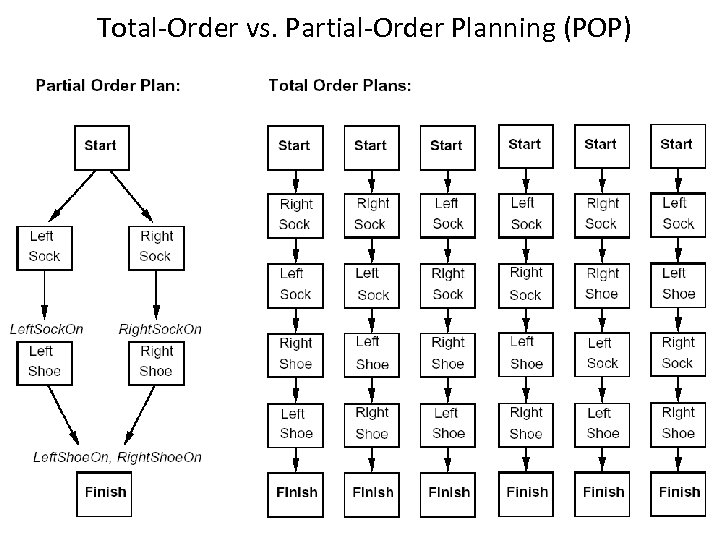Total-Order vs. Partial-Order Planning (POP) 35

Planning Techniques in Summary • Forward State Space Search • Backward State Space Search • Partial Order Planning (plan space search) • What is the state of the art technique? Sungwook Yoon

Exercise Sungwook Yoon

What is a Planning Problem? • Any problem that needs sequential decision – For a single decision, you should look for Machine Learning • Any Examples? – Free. Cell – Sokoban – Micromouse – Bridge Game – Football Sungwook Yoon

Markov Decision Process (MDP) • Sequential decision problems under uncertainty – Not just the immediate utility, but the longer-term utility as well – Uncertainty in outcomes • Roots in operations research • Also used in economics, communications engineering, ecology, performance modeling and of course, AI! – Also referred to as stochastic dynamic programs

Markov Decision Process (MDP) • Defined as a tuple: – S: State – A: Action – P: Transition function • Table P(s’| s, a), prob of s’ given action “a” in state “s” – R: Reward • R(s, a) = cost or reward of taking action a in state s • Choose a sequence of actions (not just one decision or one action) – Utility based on a sequence of decisions

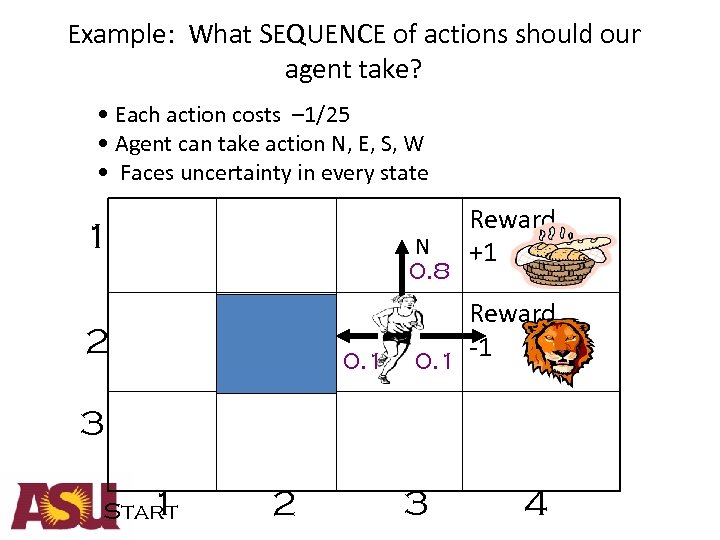Example: What SEQUENCE of actions should our agent take? • Each action costs – 1/25 • Agent can take action N, E, S, W • Faces uncertainty in every state 1 2 N 0. 8 Blocked CELL 0. 1 Reward +1 Reward -1 0. 1 3 1 Start 2 3 4

MDP Tuple: • S: State of the agent on the grid (4, 3) – Note that cell denoted by (x, y) • A: Actions of the agent, i. e. , N, E, S, W • P: Transition function – Table P(s’| s, a), prob of s’ given action “a” in state “s” – E. g. , P( (4, 3) | (3, 3), N) = 0. 1 – E. g. , P((3, 2) | (3, 3), N) = 0. 8 – (Robot movement, uncertainty of another agent’s actions, …) • R: Reward (more comments on the reward function later) – R( (3, 3), N) = -1/25 – R (4, 1) = +1

? ? Terminology • Before describing policies, lets go through some terminology • Terminology useful throughout this set of lectures • Policy: Complete mapping from states to actions

MDP Basics and Terminology An agent must make a decision or control a probabilistic system • Goal is to choose a sequence of actions for optimality • Defined as • MDP models: – Finite horizon: Maximize the expected reward for the next n steps – Infinite horizon: Maximize the expected discounted reward. – Transition model: Maximize average expected reward per transition. – Goal state: maximize expected reward (minimize expected cost) to some target state G.

? ? ? Reward Function • According to chapter 2, directly associated with state – Denoted R(I) – Simplifies computations seen later in algorithms presented • Sometimes, reward is assumed associated with state, action – R(S, A) – We could also assume a mix of R(S, A) and R(S) • Sometimes, reward associated with state, action, destination-state – R(S, A, J) – R(S, A) = S R(S, A, J) * P(J | S, A) J

Markov Assumption • Markov Assumption: Transition probabilities (and rewards) from any given state depend only on the state and not on previous history • Where you end up after action depends only on current state – After Russian Mathematician A. A. Markov (1856 -1922) – (He did not come up with markov decision processes however) – Transitions in state (1, 2) do not depend on prior state (1, 1) or (1, 2)

? ? ? MDP vs POMDPs • Accessibility: Agent’s percept in any given state identify the state that it is in, e. g. , state (4, 3) vs (3, 3) – Given observations, uniquely determine the state – Hence, we will not explicitly consider observations, only states • Inaccessibility: Agent’s percepts in any given state DO NOT identify the state that it is in, e. g. , may be (4, 3) or (3, 3) – Given observations, not uniquely determine the state – POMDP: Partially observable MDP for inaccessible environments • We will focus on MDPs in this presentation.

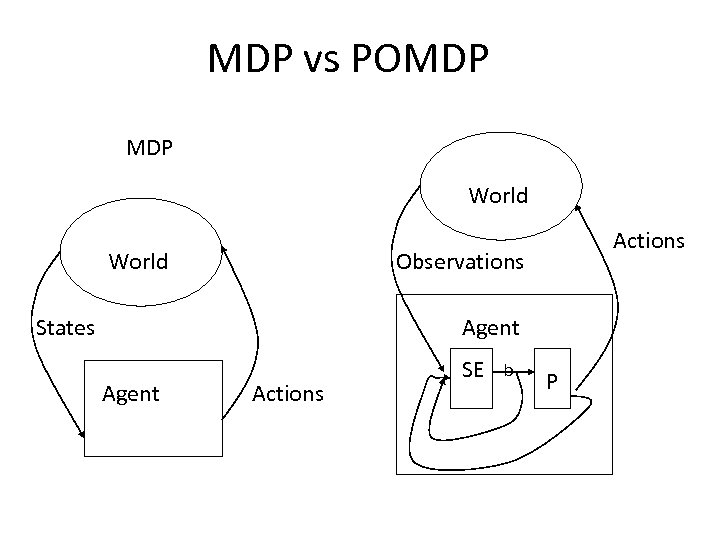MDP vs POMDP World Actions Observations States Agent Actions SE b P

Policy • Policy is like a plan – Certainly, generated ahead of time, like a plan • Unlike traditional plans, it is not a sequence of actions that an agent must execute – If there are failures in execution, agent can continue to execute a policy • Prescribes an action for all the states • Maximizes expected reward, rather than just reaching a goal state

MDP problem • The MDP problem consists of: – Finding the optimal control policy for all possible states; – Finding the sequence of optimal control functions for a specific initial state – Finding the best control action(decision) for a specific state.

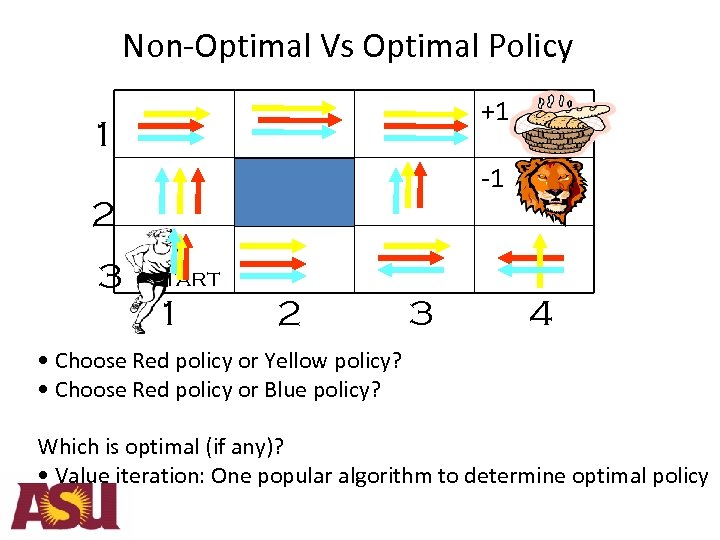Non-Optimal Vs Optimal Policy +1 1 -1 2 3 Start 1 2 3 4 • Choose Red policy or Yellow policy? • Choose Red policy or Blue policy? Which is optimal (if any)? • Value iteration: One popular algorithm to determine optimal policy

Value Iteration: Key Idea • Iterate: update utility of state “I” using old utility of neighbor states “J”; given actions “A” – U t+1 (I) = max [R(I, A) + S P(J|I, A)* U t (J)] A J – P(J|I, A): Probability of J if A is taken in state I – max F(A) returns highest F(A) – Immediate reward & longer term reward taken into account

Value Iteration: Algorithm • Initialize: U 0 (I) = 0 • Iterate: U t+1 (I) = max [ R(I, A) + S P(J|I, A)* U t (J) ] A J – Until close-enough (U t+1, Ut) • At the end of iteration, calculate optimal policy: Policy(I) = argmax [R(I, A) + S P(J|I, A)* U t+1 (J) ] A J

MDP Solution Techniques • • • Value Iteration Policy Iteration Matrix Inversion Linear Programming LAO* Sungwook Yoon

Planning vs. MDP • Common – Try to act better • Difference – Relational vs. Propositional – Symbolic vs. Value – Less Toyish vs. More Toyish – Solution Techniques – Classic vs. More General Sungwook Yoon

Planning vs. MDP, recent trends • Recent Trend in Planning – Add diverse aspect • Probabilistic, Temporal, Oversubscribed. . Etc – Getting closer to MDP but with Relational Representation • More real-world like. . • Recent Trend in MDP – More structure • Relational, Options, Hierarchy, Finding Harmonic Functions … – Getting closer to Planning! Sungwook Yoon

Planning better than MDP? • They deal with different objectives – MDP focused more on optimality in general planning setting • The size of the domain is too small – Planning focused on classic setting (unrealistic) • Well, still many interesting problems can be coded into classic setting • Sokoban, Free. Cell • Planning’s biggest advances is from fast preprocessing of the relational problems – Actually, they turn the problems into propositional ones. Sungwook Yoon

Can we solve real world problems? • Suppose all the Planning and MDP techniques are well developed. – Temporal, Partial Observability, Continuous Variable, etc. • Well, who will code such problems into AI agent? • Should consider the cost of developing such problem definition and developing “very” general Planner – Might be better with domain specific planner • Sokoban solver, Free. Cell solver etc. Sungwook Yoon

What is AI? • An AI is 99 percent Engineering and 1 percent Intelligent Algorithms – Sungwook Yoon