Artificial Intelligence 9 Resolution Theorem Proving Course V

Artificial Intelligence 9. Resolution Theorem Proving Course V 231 Department of Computing Imperial College Jeremy Gow

The Full Resolution Rule l If Unify(Pj, ¬Qk) = (¬ makes them unifiable) P 1 … P m, Q 1 … Qn Subst( , P 1 … (no Pj) … Pm Q 1 … (no Qk). . . Qn) l l l Pj and Qk are resolved Arbitrary number of disjuncts Relies on preprocessing into CNF

A More Concise Version E. g. for A = {1, 2, 7} first clause is L 1 L 2 L 7

Resolution Proving l Knowledge base of clauses – l Resolve pairs of clauses – – l Start with the axioms and negation of theorem in CNF Usingle rule of inference (full resolution) Resolved sentence contains fewer literals Proof ends with the empty clause – – Signifies a contradiction Must mean the negated theorem is false l – (Because the axioms are consistent) Therefore the original theorem was true

Empty Clause means False l Resolution theorem proving ends – l When the resolved clause has no literals (empty) This can only be because: – Two unit clauses were resolved l – l One was the negation of the other (after substitution) Example: q(X) and ¬q(X) or: p(X) and ¬p(bob) Hence if we see the empty clause – – This was because there was an inconsistency Hence the proof by refutation

Resolution as Search l l l Initial State: Knowledge base (KB) of axioms and negated theorem in CNF Operators: Resolution rule picks 2 clauses and adds new clause Goal Test: Does KB contain the empty clause? Search space of KB states We want proof (path) or just checking (artefact)

Aristotle’s Example (Again) l l Socrates is a man and all men are mortal Therefore Socrates is mortal Initial state 1) is_man(socrates) 2) is_man(X) is_mortal(X) 3) ¬is_mortal(socrates) (negation of theorem) l Resolving (1) & (2) gives new state (1)-(3) & 4) is_mortal(socrates)

Aristotle’s Example: Search Space 1) is_man(socrates) 2) is_man(X) is_mortal(X) 3) ¬is_mortal(socrates) 4) is_mortal(socrates) 1) is_man(socrates) 2) ¬is_man(X) is_mortal(X) 3) ¬is_mortal(socrates) 4) ¬is_man(socrates) 1) is_man(socrates) 2) is_man(X) is_mortal(X) 3) ¬is_mortal(socrates) 4) is_mortal(socrates) 5) False 1) is_man(socrates) 2) is_man(X) is_mortal(X) 3) ¬is_mortal(socrates) 4) ¬is_man(socrates) 5) False

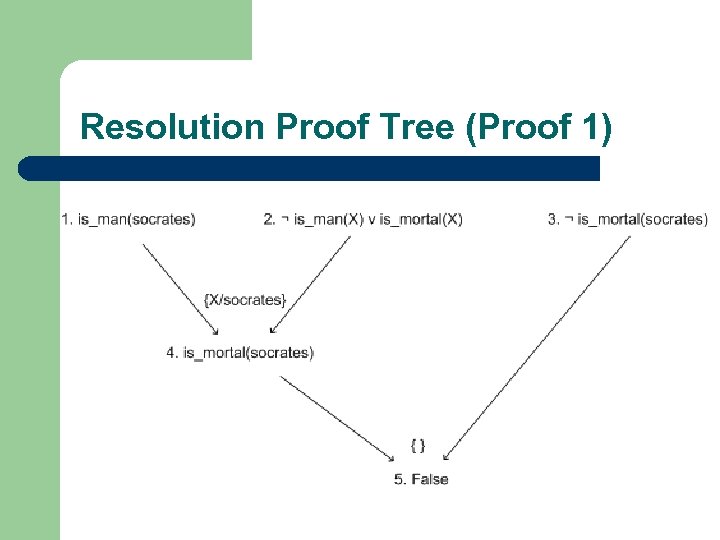Resolution Proof Tree (Proof 1)

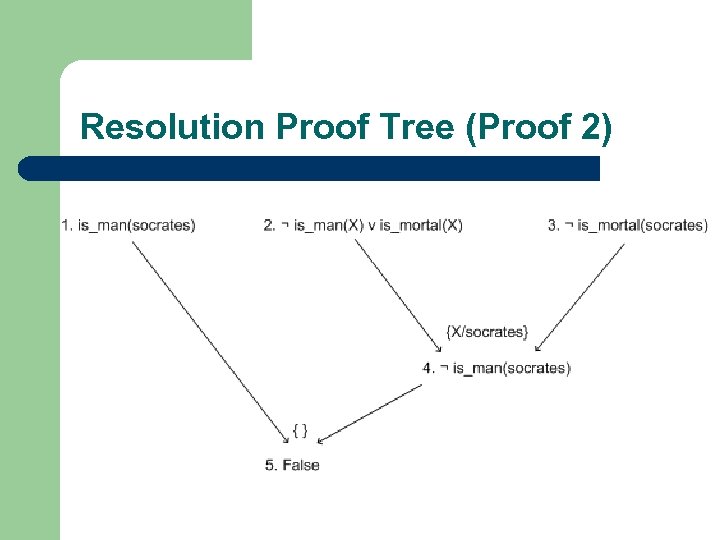Resolution Proof Tree (Proof 2)

Reading Proof Tree 2 You said that all men were mortal. That means that for all things X, either X is not a man, or X is mortal [CNF step]. If we assume that Socrates is not mortal, then, given your previous statement, this means Socrates is not a man [first resolution step]. But you said that Socrates is a man, which means that our assumption was false [second resolution step], so Socrates must be mortal.

Russell & Norvig Example

Reminder: Kowalski NF l Can reintroduce to CNF, e. g. ¬A ¬C B becomes (A C) B l l Kowalski normal form (A 1 … An) (B 1 … Bn) Resolve in KNF using ‘KNF style’ rules – e. g. Binary resolution… A B, B C A C

R&N Example: Kowalski NF

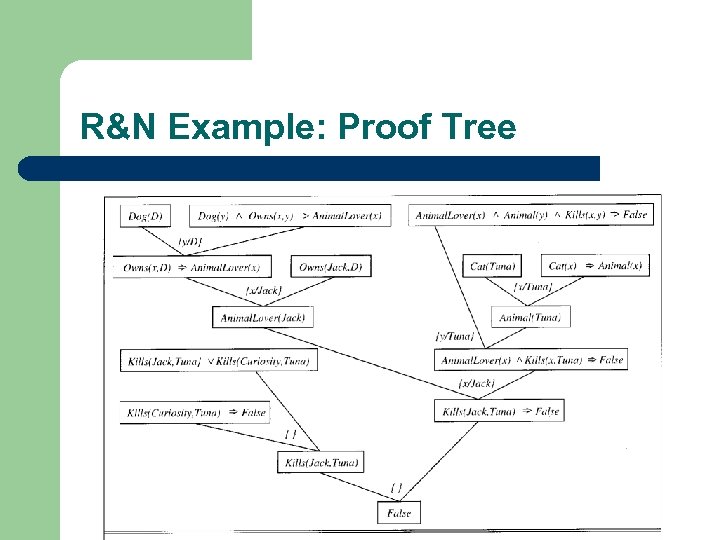R&N Example: Proof Tree

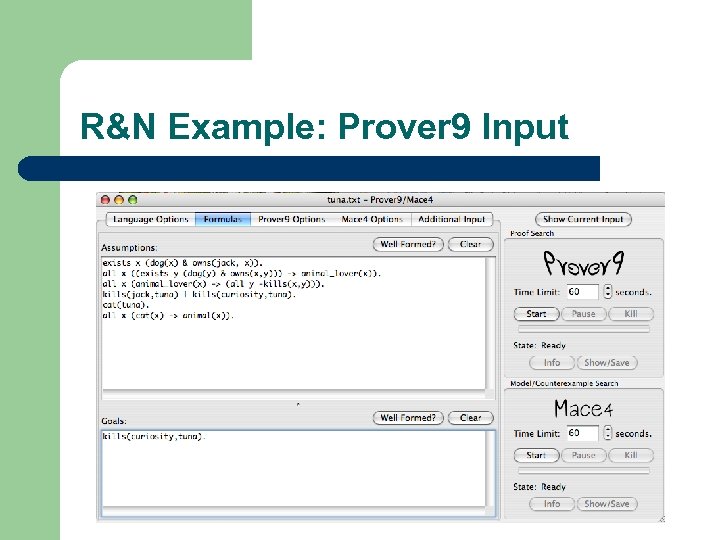R&N Example: Prover 9 Input

R&N Example: Prover 9 Proof

Equality Axioms l is_pres(obama) and is_pres(b_obama) – will not unify (syntactically different) l – Even if we add to the knowledge base: l l unification algorithm does not allow this obama = b_obama Solution: add equality axioms to KB – – X=X, X=Y Y=X, etc. Special axiom for every predicate/function: l X = Y P(X) = P(Y)

Equality & Demodulation l l Alternative solution: rewrite with equalities Demodulation inference rule X=Y, A[S] Unify(X, S) = Subst( , A[Y]) – – Two input clauses (one an equality X=Y) Unify X with a subterm S of other Apply unifier to clause with subterm Y (not S) Also works unifying with Y and putting in X

Heuristic Strategies l l Pure resolution search tends to be slow For interesting problems – – – l Selection Heuristics – l Many clauses in the initial knowledge base Each step adds a new clause (which can be used) Num. of possible resolution combinations explodes Intelligently choose which pair to resolve Pruning Heuristics – Forbid certain pairs

Unit Preference Strategy l Prefer to resolve unit clauses – – l Searching for smallest (empty) clause – l Contain only a single literal Selection heuristic Resolving with the unit clauses keeps small Very effective early on for simple problems – Doesn’t reduce branching rate for medium problems

Set of Support Strategy l Distinguished subset of KB clauses – – Set of support (SOS) clauses Every step must involve SOS (pruning heuristic) l Must be careful not to lose completeness l Example SOS strategy: – – – l Initial SOS is negated theorem Add new clauses to SOS Hence False will be deduced (strategy is complete) Many provers use SOS, e. g. Prover 9

Input Resolution Strategy l Special case of SOS strategy – l Clearly reduces search space – – l l SOS = clauses in the initial knowledge base Every resolution must involve an original clause So number of possible resolutions grows slowly Not complete for first order logic But complete for Horn-clauses, e. g. Prolog

Subsumption l Clause C subsumes clause D – l Naive check for subsumption – – – l if C is more ‘general’ (D is more specific) Select C 2, a subset of literals of C Find Unify(C 2, D) = does not add anything to D (only renames vars) Example: – – – p(george) ∨ q(X) subsumed by p(A) ∨ q(B) ∨ r(C) Substitution: {A/george, X/B} Second clause is more general

Subsumption Strategy l l Check each new clause is not subsumed by KB Complete strategy – – – l Specific clauses can be inferred from general ones So we can throw specific clauses away Reduced search space still contains False Can be inefficient – expense must be outweighed by the reduction in the search space

Applications: Axioms for Algebras l Bill Mc. Cune and Larry Wos – – l Robbins Problem (axioms of Boolean algebras) – – l Argonne National Laboratories FO resolution provers: EQP, Otter, Prover 9 Stated 60+ years ago, mathematicians failed 1996: EQP solved in 8 days in 1996 (+human work) General application to algebraic axiomatisations – – Generate possible axioms for algebras Prove new axioms equivalent to old

Applications: Theory Formation l Simon’s HR system: Automated Theory Formation – l l l Theories = concepts, examples, conjectures, proofs HR uses Otter to prove conjectures it makes Effective in algebraic domains – l Used in mathematical (and bioinformatics) domains See notes for anti-associative algebra results Otter not so effective in number theory – – Used as a ‘triviality’ filter (discard theorems it can prove) Example conjectures made by HR (and proved by Simon): l l l Sum of divisors is prime → number of divisors is prime Sum of divisors of a square is an odd number Perfect numbers are pernicious [and many more…. . ]

Inductive Theorem Proving l Deduction by mathematical induction l Induction over many different structures Allows reasoning about recursion/iteration l – l Useful for hardware/software verification Don’t confuse inductive learning (next lecture)

Interactive Theorem Proving l Necessary to interact with humans in order to prove theorems of any difficulty l Mathematician’s assistant – l Let a theorem prover do simple tasks while you develop a theory (e. g. , Buchberger’s Theorema) Guided theorem prover – – User follows and guides computer proof attempt Needs visualisation tools for proof trees

Higher Order Theorem Proving l Deduction in higher order logics – – – l See lecture 4 Allows more natural and succinct statements Logics much less well-behaved HOL theorem prover – – Larry Paulson’s group in Cambridge Has been used for verification tasks l – E. g. verification of crytographic protocols Uses induction and interactive control

Proof Planning l l Initially Alan Bundy’s group in Edinburgh Human proofs often follow a similar structure – – l Outline plan guides proof search – – l Express this as a outline plan Methods represent a patterns of deduction Results in specific plan for theorem Critics deal with common problems Particularly useful for inductive theorems – Proof of base case and step case follow pattern

Databases & Competitions l TPTP library (Sutcliffe & Suttner) – – – l Thousands of Problems for Theorem Provers Benchmarks for first order provers HR is only non-human to add to this library Annual CASC competition (Sutcliffe et al. ) – – – Which is fastest/most accurate FO prover on planet? Uses blind selection from the TPTP library 2002 -08 champion: Vampire (Voronkov & Riazonov)