Argumentation Logics Lecture 5 Argumentation with structured arguments

Argumentation Logics Lecture 5: Argumentation with structured arguments (1) argument structure Henry Prakken Chongqing June 2, 2010 1

Contents n Structured argumentation: n n Arguments Argument schemes 2

Merits of Dung (1995) n Framework for nonmonotonic logics n n Comparison and properties Guidance for development From intuitions to theoretical notions But should not be used for KR 3

The structure of arguments: two approaches n Both approaches: arguments are inference trees n Assumption-based approaches (Dung-Kowalski-Toni, Besnard & Hunter, …) n n n Sound reasoning from uncertain premises Arguments attack each other on their assumptions (premises) Rule-based approaches (Pollock, Vreeswijk, …) n n Risky (‘defeasible’) reasoning from certain premises Arguments attack each other on applications of defeasible inference rules 4

Aspic framework: overview Argument structure: n Trees where n n Nodes are wff of a logical language L Links are applications of inference rules n n n Rs = Strict rules ( 1, . . . , 1 ); or Rd= Defeasible rules ( 1, . . . , 1 ) Reasoning starts from a knowledge base K L Defeat: attack on conclusion, premise or inference, + preferences Argument acceptability based on Dung (1995) 5

Argumentation systems n An argumentation system is a tuple AS = (L, -, R, ) where: n n n L is a logical language - is a contrariness function from L to 2 L R = Rs Rd is a set of strict and defeasible inference rules is a partial preorder on Rd If -( ) then: n n if -( ) then is a contrary of ; if -( ) then and are contradictories _ _ n = , = 6

Knowledge bases n A knowledge base in AS = (L, -, R, = ’) is a pair (K, =<’) where K L and ’ is a partial preorder on K/Kn. Here: n n n Kn = (necessary) axioms Kp = ordinary premises Ka = assumptions 7

Structure of arguments n An argument A on the basis of (K, ’) in (L, -, R, ) is: n if K with n n A 1, . . . , An if there is a strict inference rule Conc(A 1), . . . , Conc(An) n n Conc(A) = { } Sub(A) = Def. Rules(A) = Conc(A) = { } Sub(A) = Sub(A 1) . . . Sub(An) {A} Def. Rules(A) = Def. Rules(A 1) . . . Def. Rules(An) A 1, . . . , An if there is a defeasible inference rule Conc(A 1), . . . , Conc(An) n n n Conc(A) = { } Sub(A) = Sub(A 1) . . . Sub(An) {A} Def. Rules(A) = Def. Rules(A 1) . . . Def. Rules(An) {A 1, . . . , An } 8

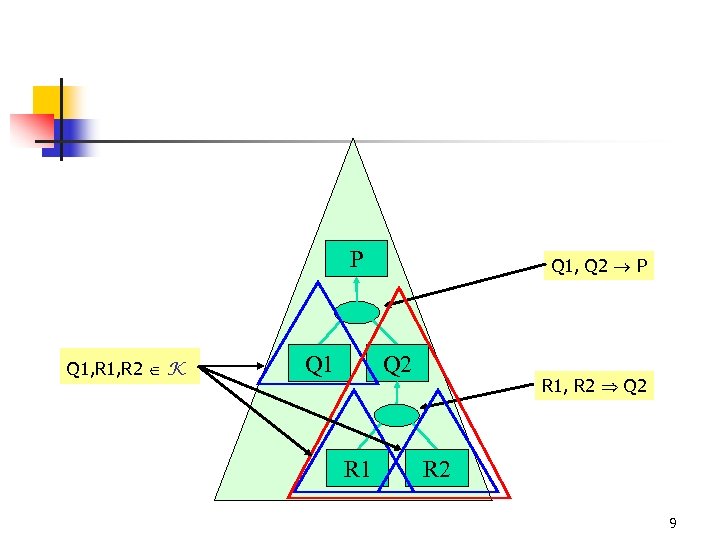P Q 1, R 2 K Q 1, Q 2 P Q 2 R 1, R 2 Q 2 R 2 9

Example R: n r 1: n r 2: n r 3: n r 4: n r 5: n r 6: n r 7: n r 8: p q p, q r s t t ¬r 1 u v v, q ¬t p, v ¬s s ¬p Kn = {p}, Kp = {s, u} 10

Types of arguments n An argument A is: n n n Strict if Def. Rules(A) = Defeasible if not Firm if Prem(A) Kn Plausible if not firm S |- means there is a strict argument A s. t. n n Conc(A) = Prem(A) S 11

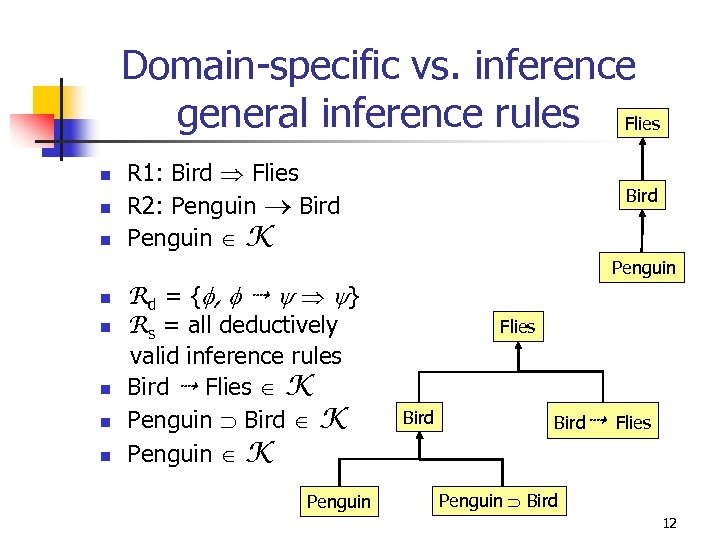Domain-specific vs. inference general inference rules Flies n n n R 1: Bird Flies R 2: Penguin Bird Penguin K Bird Penguin n n Rd = { , } Rs = all deductively valid inference rules Bird Flies K Penguin Bird K Penguin Flies Bird Flies Penguin Bird 12

Argument(ation) schemes: general form Premise 1, …, Premise n Therefore (presumably), conclusion n n Defeasible inference rules! But also critical questions n Negative answers are counterarguments 13

Expert testimony (Walton 1996) E is expert on D E says that P P is within D Therefore (presumably), P is the case n Critical questions: n n n Is E biased? Is P consistent with what other experts say? Is P consistent with known evidence? 14

Witness testimony W says P W was in the position to observe P Therefore (presumably), P n Critical questions: n n n Is W sincere? Does W’s memory function properly? Did W’s senses function properly? 15

Arguments from consequences Action A brings about G, G is good Therefore (presumably), A should be done n Critical questions: n n n Does A also have bad consequences? Are there other ways to bring about G? . . . 16

Temporal persistence (Forward) P is true at T 1 and T 2 > T 1 Therefore (presumably), P is still true at T 2 n Critical questions: n n Was P known to be false between T 1 and T 2? Is the gap between T 1 and T 2 too long? 17

Temporal persistence (Backward) P is true at T 1 and T 2 < T 1 Therefore (presumably), P was already true at T 2 n Critical questions: n n Was P known to be false between T 1 and T 2? Is the gap between T 1 and T 2 too long? 18

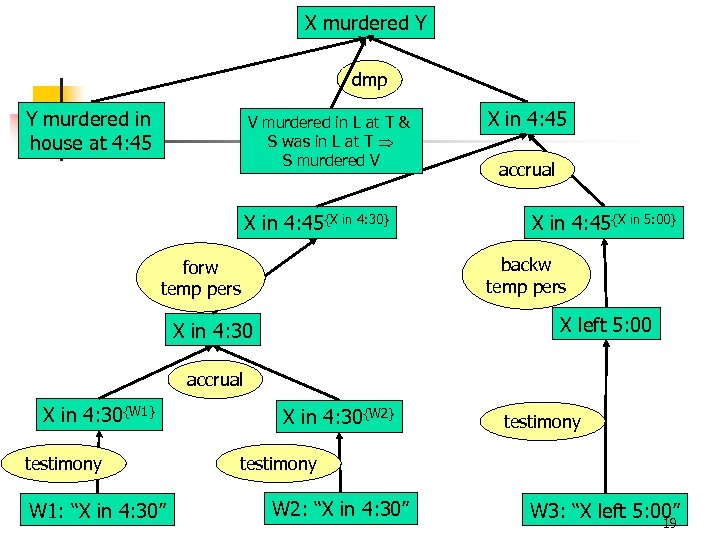X murdered Y dmp Y murdered in house at 4: 45 V murdered in L at T & S was in L at T S murdered V X in 4: 45{X in 4: 30} X in 4: 45 accrual X in 4: 45{X in 5: 00} backw temp pers forw temp pers X left 5: 00 X in 4: 30 accrual X in 4: 30{W 1} testimony W 1: “X in 4: 30” X in 4: 30{W 2} testimony W 2: “X in 4: 30” W 3: “X left 5: 00” 19