Areas Bound By Two Curves. Area Bound By


Areas Bound By Two Curves
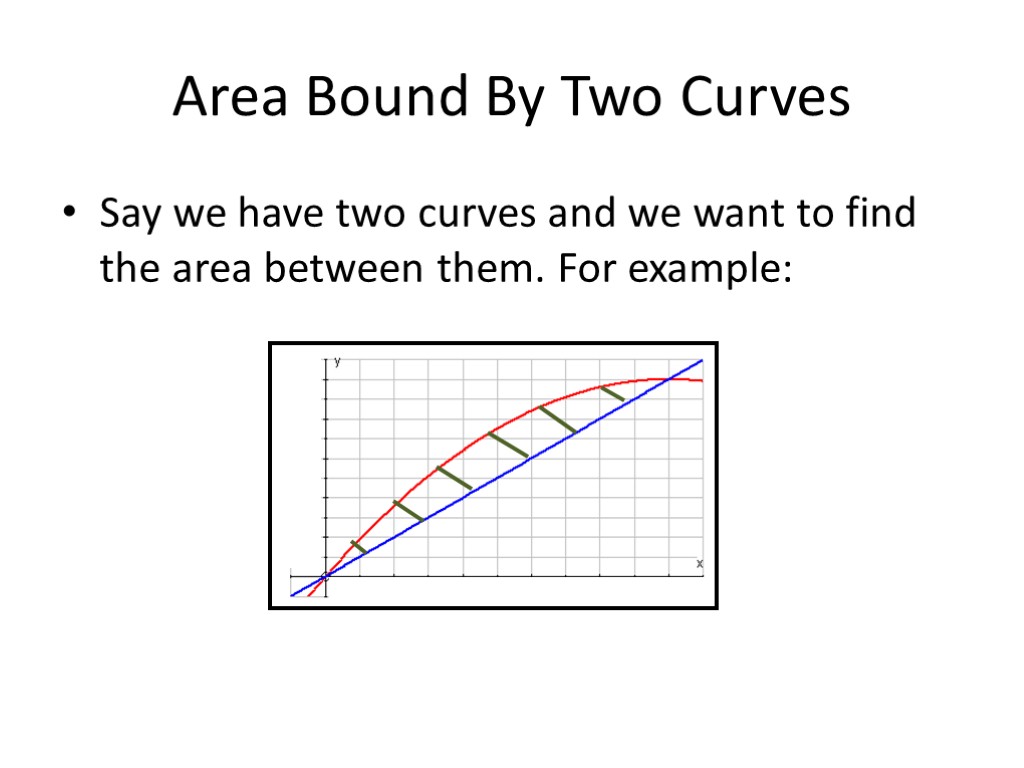
Area Bound By Two Curves Say we have two curves and we want to find the area between them. For example:
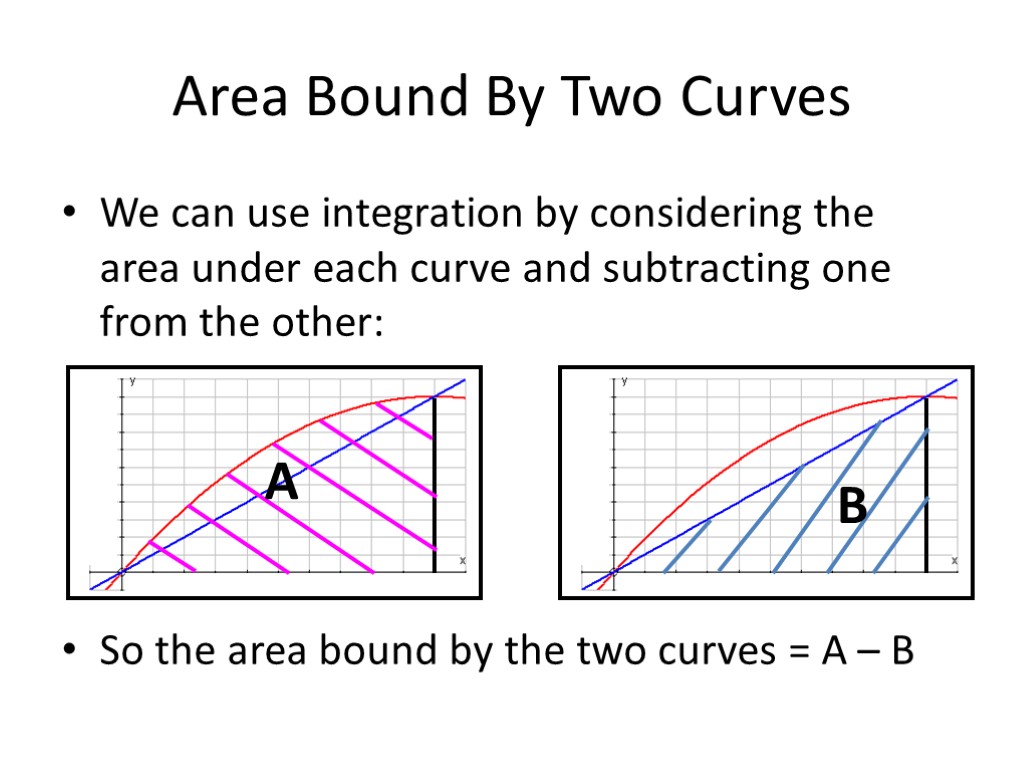
Area Bound By Two Curves We can use integration by considering the area under each curve and subtracting one from the other: So the area bound by the two curves = A – B A B

Area Bound By Two Curves To calculate the area we need to know the equations of the lines. Given: We can then find the intersection points which will gives us the limits of integration.
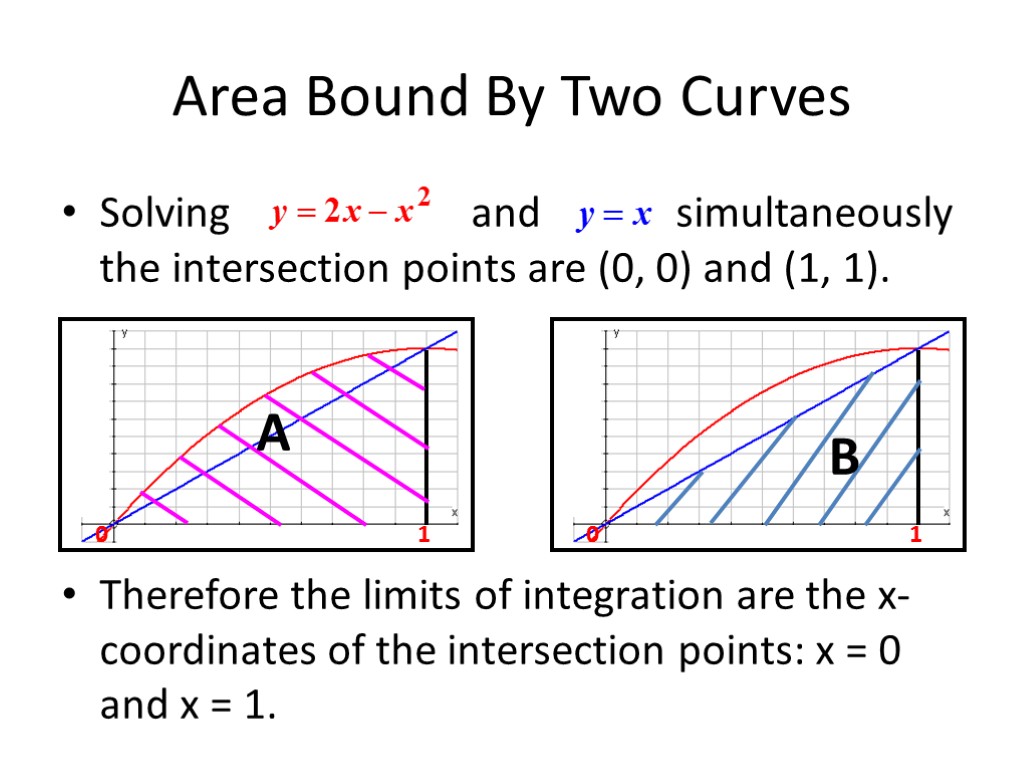
Area Bound By Two Curves Solving and simultaneously the intersection points are (0, 0) and (1, 1). Therefore the limits of integration are the x-coordinates of the intersection points: x = 0 and x = 1.
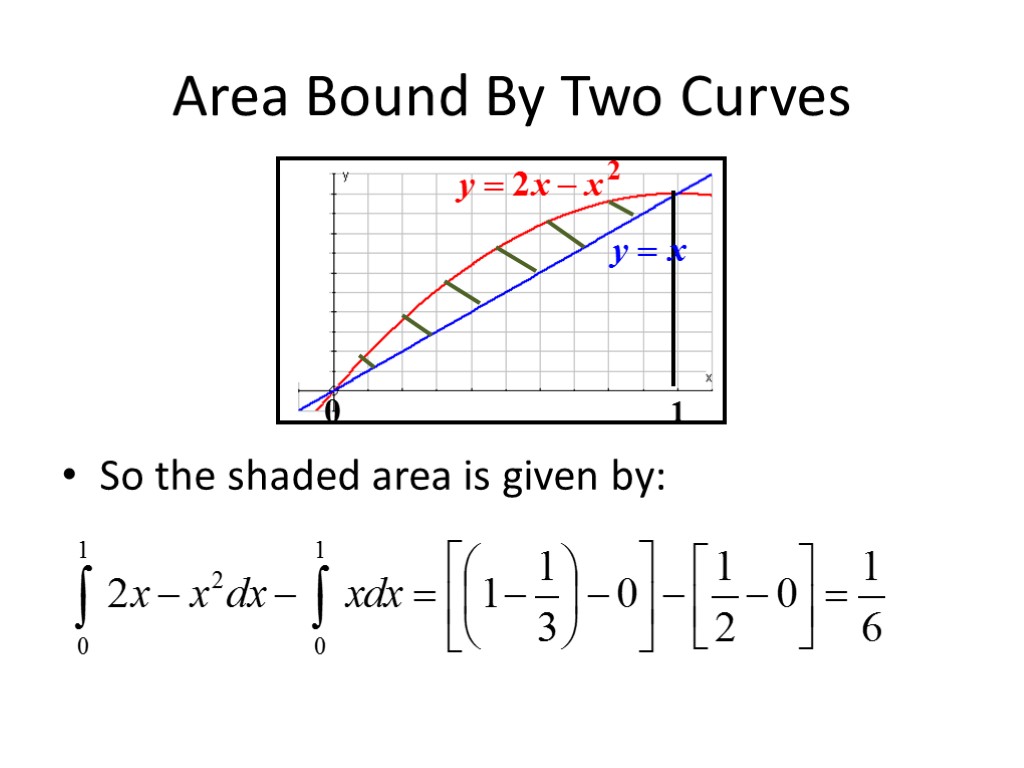
Area Bound By Two Curves So the shaded area is given by:

Example 1 Find the area bound by the following curves: Firstly we need to know the intersection points:

Example 1 Secondly we need to know which is the upper curve. Both curves are quadratics and so we can consider the vertices of each curve to ascertain which one is above the other. We can do this by completing the square. . is already in completed square form with a vertex at (0, -2)

Example 1 Since then the vertex of is above the vertex of and therefore to find the area between the two curves we find

Extension to Example 1 In the above example, the curves cross the x axis in the given interval. Given that integrating a single function that is below the x axis gives a negative result and that previously if the function was partly above and partly below the x axis we had to split the integral at the point where the function crossed the x axis, why do we not have to split the integral here?
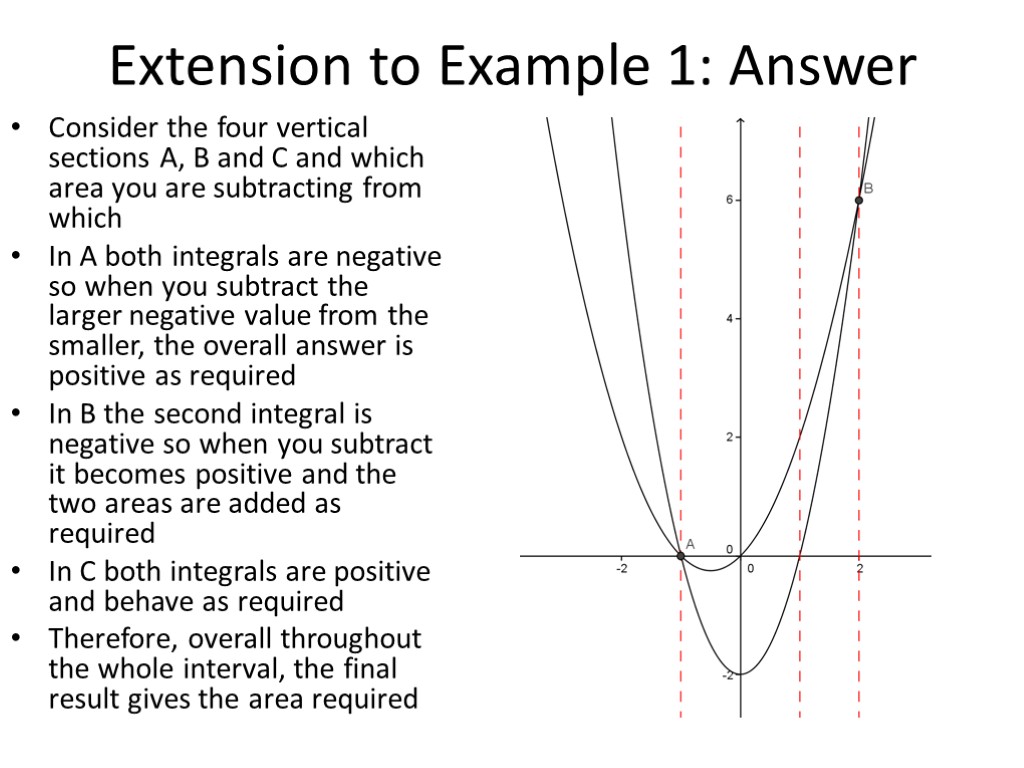
Extension to Example 1: Answer Consider the four vertical sections A, B and C and which area you are subtracting from which In A both integrals are negative so when you subtract the larger negative value from the smaller, the overall answer is positive as required In B the second integral is negative so when you subtract it becomes positive and the two areas are added as required In C both integrals are positive and behave as required Therefore, overall throughout the whole interval, the final result gives the area required

Example 2 Find the area of the region of the xy plane defined by the inequalities: Firstly if we consider the two regions graphically by sketching the graphs:
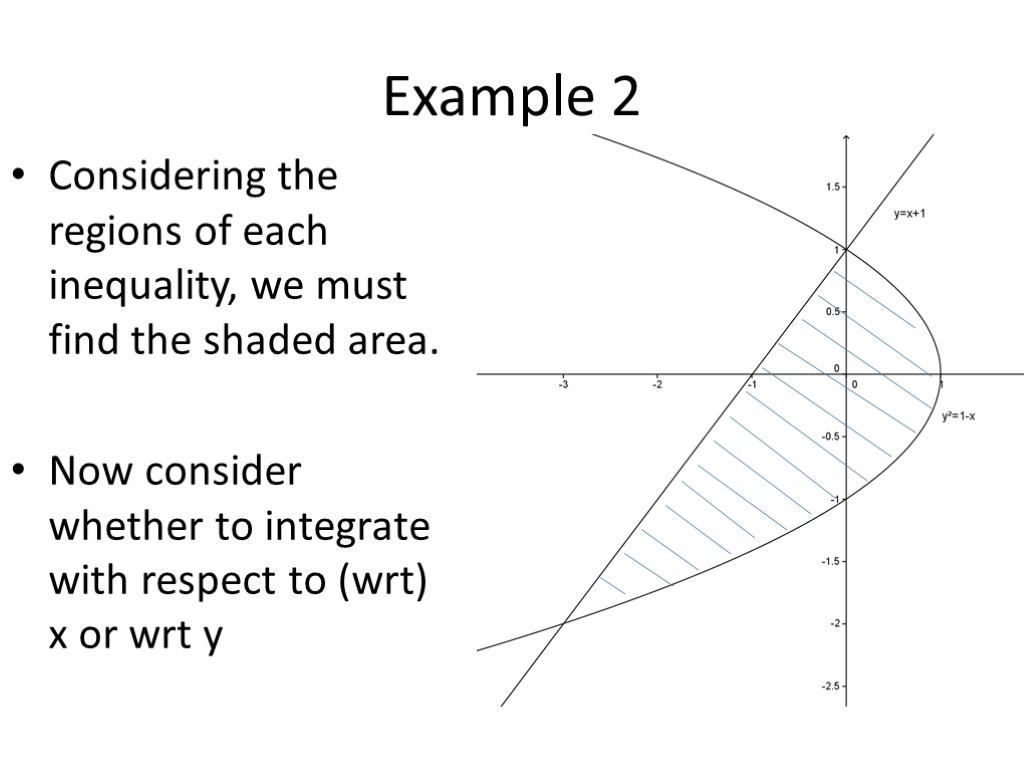
Example 2 Considering the regions of each inequality, we must find the shaded area. Now consider whether to integrate with respect to (wrt) x or wrt y
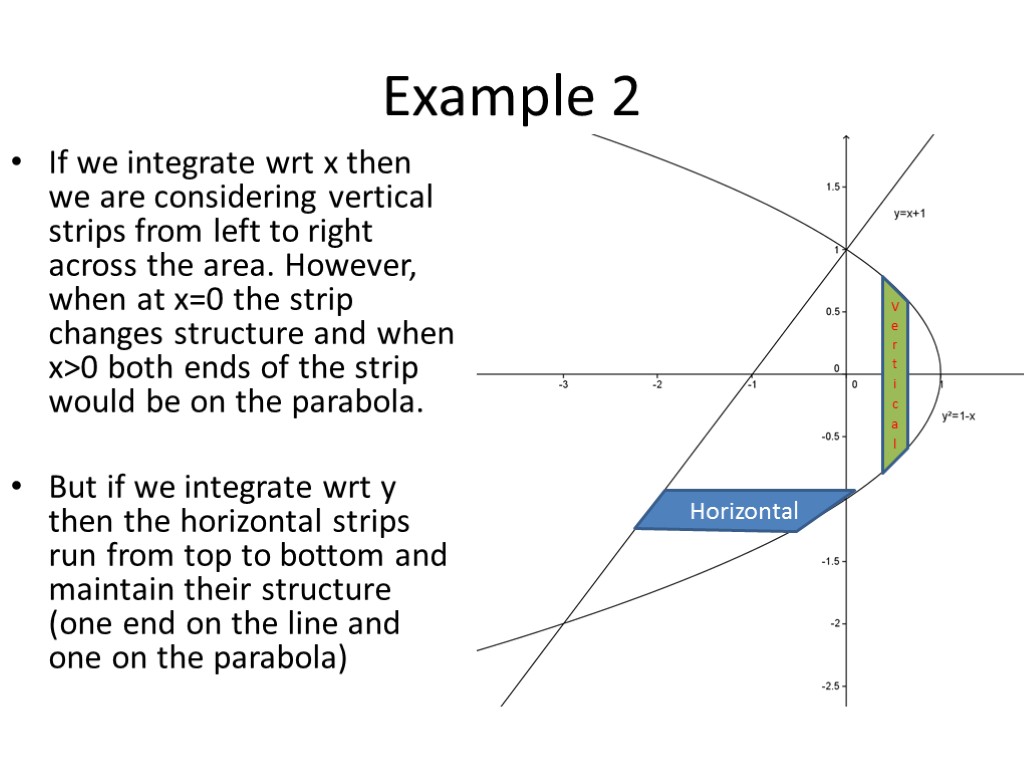
Example 2 If we integrate wrt x then we are considering vertical strips from left to right across the area. However, when at x=0 the strip changes structure and when x>0 both ends of the strip would be on the parabola. But if we integrate wrt y then the horizontal strips run from top to bottom and maintain their structure (one end on the line and one on the parabola) Horizontal Vertical
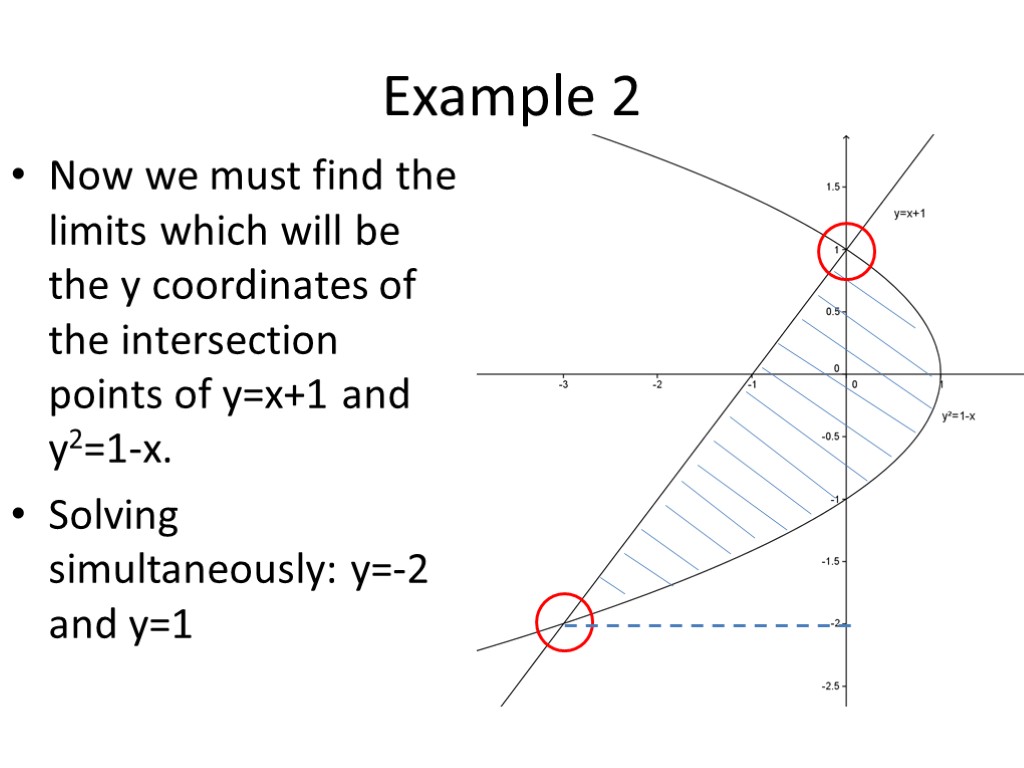
Example 2 Now we must find the limits which will be the y coordinates of the intersection points of y=x+1 and y2=1-x. Solving simultaneously: y=-2 and y=1

Example 2 Finally, so that we can integrate wrt y, we must make x the subject of the equations: x=1-y2 and x=y-1 We found that finding an area with the y axis equated to an area to the left of the curve so to find our area we must subtract the area to the left of x=y-1 from the area to the left of x=1-y2

Example 2 This equates to the following integration:
9_areas_bound_by_two_curves.ppt
- Количество слайдов: 17

