Area Perimeter Volume Area Perimeter of

Area, Perimeter & Volume Area & Perimeter of Irregular Shapes Parallelogram Circumference & Area of circles Circumference & Area of arcs/sectors Circle Problems Net/surface area of 3 D shapes Volume Prisms Drawing to Scale Revision Exercises

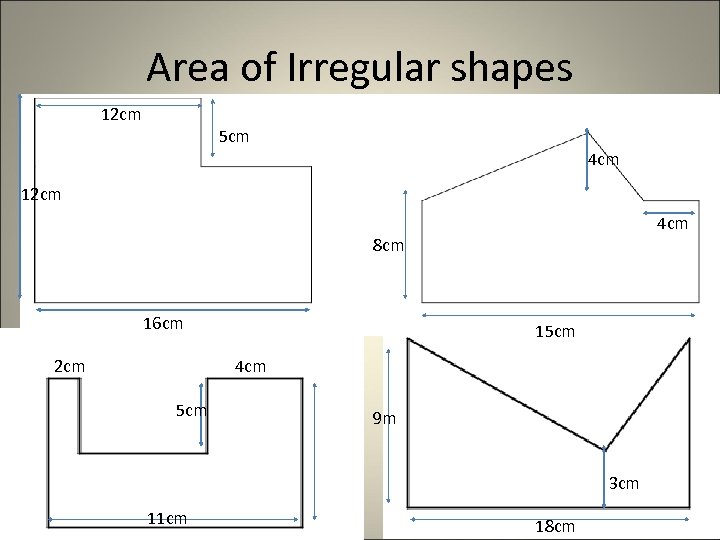Area of Irregular shapes 12 cm 5 cm 4 cm 12 cm 4 cm 8 cm 16 cm 2 cm 15 cm 4 cm 5 cm 9 m 3 cm 11 cm 18 cm

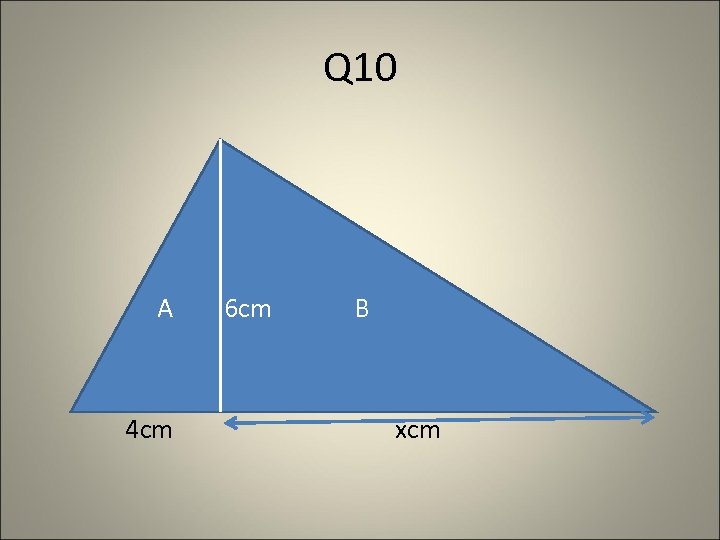Q 10 A 4 cm 6 cm B xcm

Q 13 page 88 (i) Formula: A=lxw 28 = 7 x (x) 28 = 7 x ²⁸⁄₇ = 7 x⁄₇ 4=x x=4 (i) Formula: A = ½(b x h) 120 = ½(15 x y) 120 = ½(15 y) 120 = 7½y ¹²⁰⁄7½ = 7½y⁄7½ 16 = y y = 16

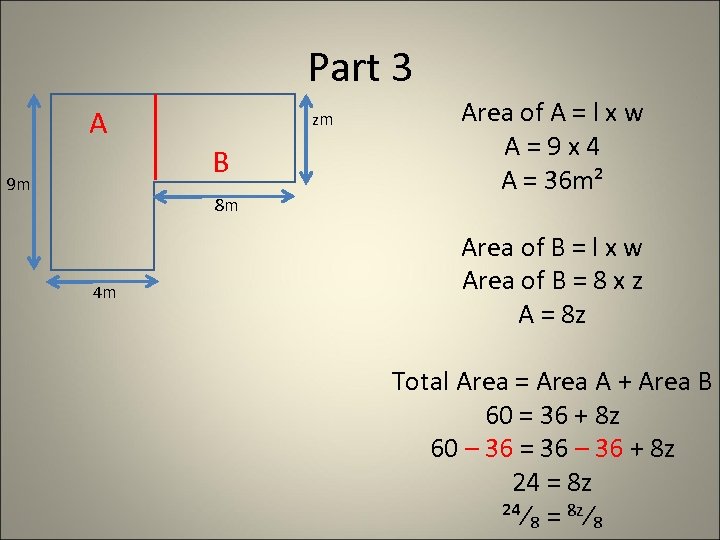Part 3 A 9 m zm B 8 m 4 m Area of A = l x w A=9 x 4 A = 36 m² Area of B = l x w Area of B = 8 x z A = 8 z Total Area = Area A + Area B 60 = 36 + 8 z 60 – 36 = 36 – 36 + 8 z 24 = 8 z ²⁴⁄₈ = 8 z⁄₈

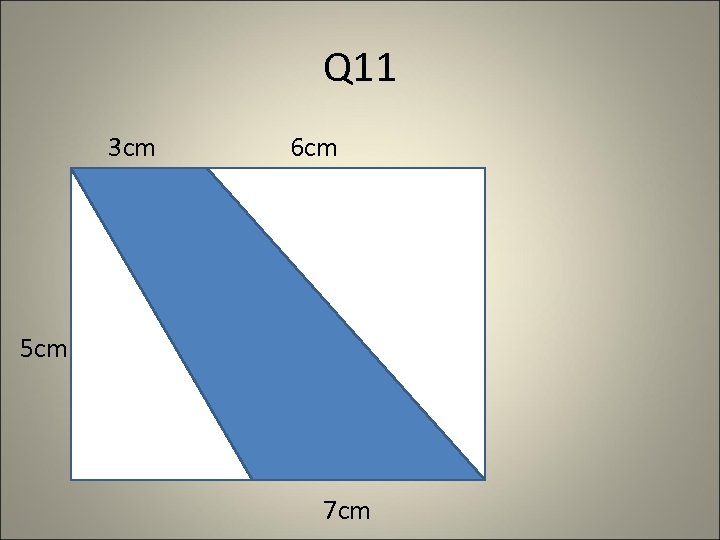Q 11 3 cm 6 cm 5 cm 7 cm

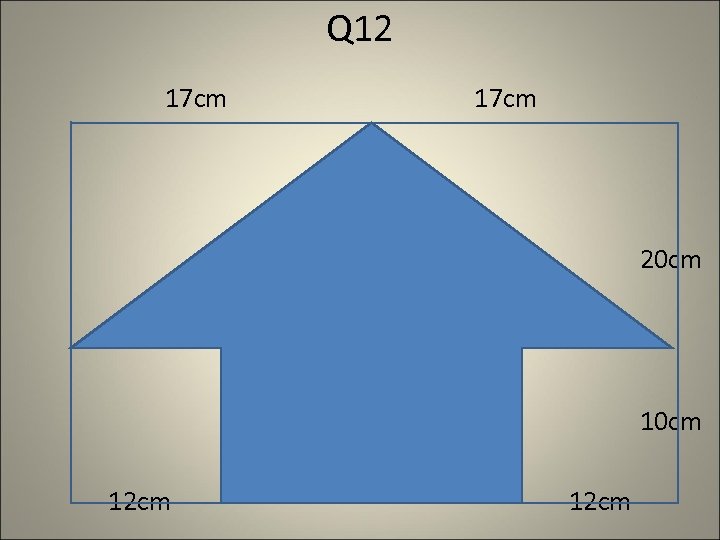Q 12 17 cm 20 cm 12 cm

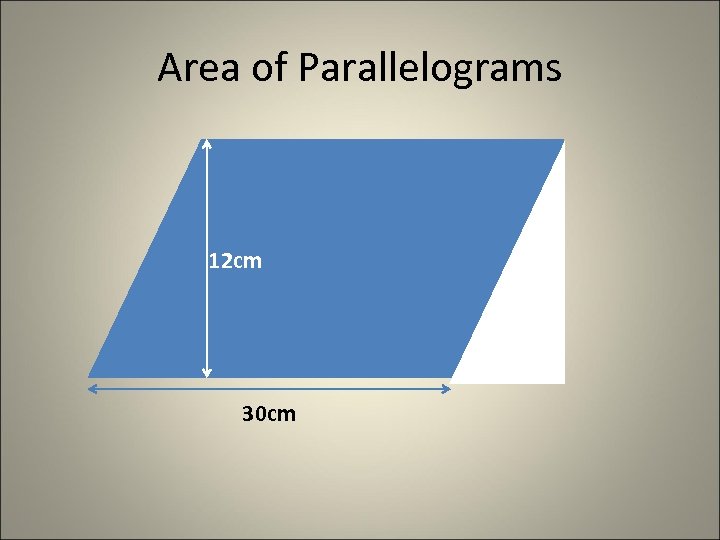Area of Parallelograms 12 cm 30 cm

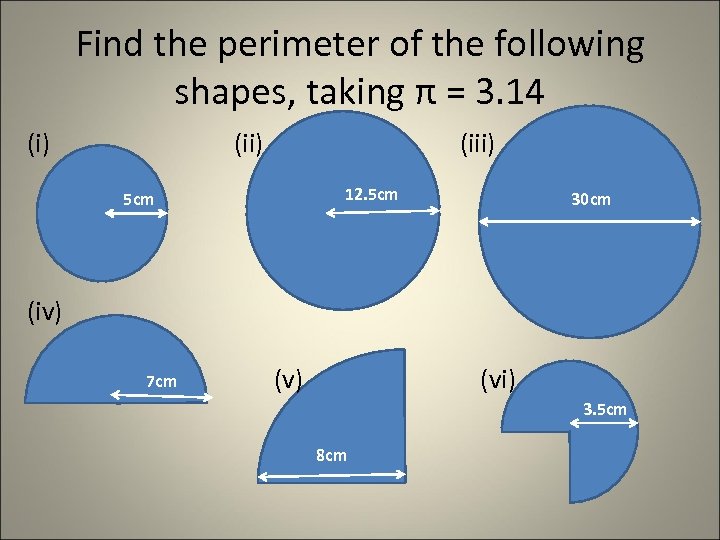Find the perimeter of the following shapes, taking π = 3. 14 (i) (iii) 12. 5 cm 30 cm (iv) 7 cm (v) (vi) 3. 5 cm 8 cm

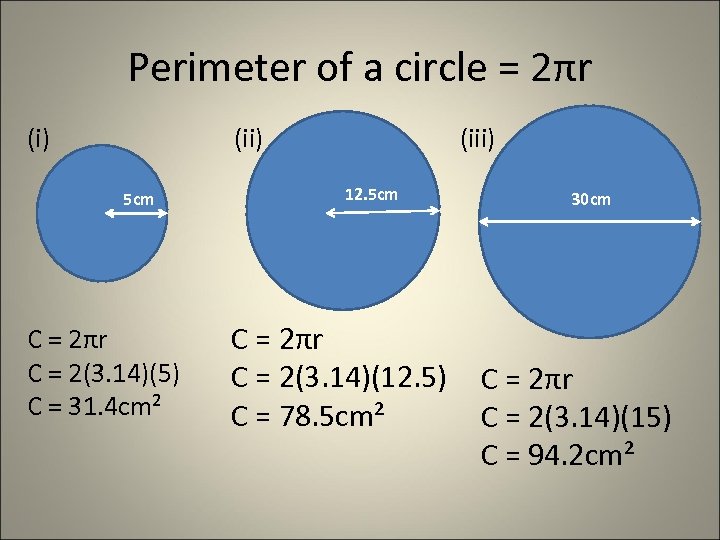Perimeter of a circle = 2πr (i) (ii) 5 cm C = 2πr C = 2(3. 14)(5) C = 31. 4 cm² (iii) 12. 5 cm C = 2πr C = 2(3. 14)(12. 5) C = 78. 5 cm² 30 cm C = 2πr C = 2(3. 14)(15) C = 94. 2 cm²

(iv) Find the perimeter of the following shapes, taking π = 3. 14 (iv) 7 cm C = 2πr C =2(3. 14)(7) C = 43. 96 C = ½(43. 96) C = 21. 98 + 14 = 35. 98 8 cm C = 2πr C =2(3. 14)(8) C = 50. 24 C =¼(50. 24) C = 12. 56 + 8 3. 5 cm C = 2πr C =2(3. 14)(3. 5) C = 21. 98 C =¾(21. 98) C = 16. 485 + 3. 5 = 23. 485

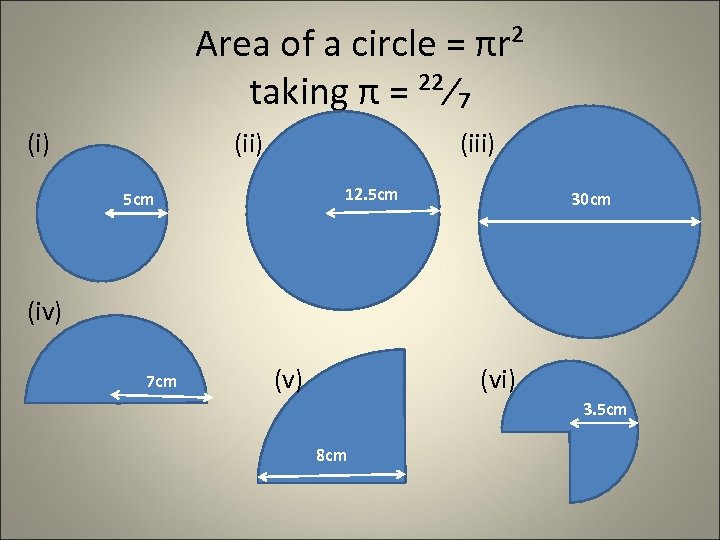Area of a circle = πr² taking π = ²²⁄₇ (i) (iii) 12. 5 cm 30 cm (iv) 7 cm (v) (vi) 3. 5 cm 8 cm

Find the area of the following shapes, using the value for π on your calculator 23 cm A = πr² A = π(11. 5)² A = 415. 46 cm² 8. 5 cm 120⁰ A = πr² ¹²⁰⁄₃₆₀ = ⅓ A = ⅓πr² A = ⅓π(8. 5)² A = 75. 66 12 cm 60⁰ A = πr² ⁶⁰⁄₃₆₀ = ⅙ A = ⅙πr² A = ⅙π(12)² A = 75. 39822

In terms of π Find the area and circumference of the following circles in terms of π 7 cm Area = πr² A = π(7)² A = 49π cm² Circum. = 2πr C = 2π(7) C = 14π 16 cm Area = πr² A = π(78)² A = 64π cm² Circum. = 2πr C = 2π(8) C = 16π

Area and perimeter problems Q 13 Q 12 63 m 101 m C = 2πr C = 2(²²⁄₇)(31. 5) C = 198 m Total Perimeter =198 + 101 = 400 m 10, 000 ÷ 400 = 25 laps 8 cm Outer Circle: Radius = 16 cm C = 2πr C = 2(3. 14)(16) C = 100. 48 cm 16 cm Inner Circle: Radius = 8 cm C = 2πr C = 2(8)(3. 14) C = 50. 24 Total Perimeter: 100. 48 + 50. 24 + 8 = 166. 72

Finding the area 8 cm Area of large semi circle A = ½ πr² A = ½(3. 14)(16)² A = 401. 92 16 cm Area of small semi circle A = ½πr² A = ½(3. 14)(8)² A = 100. 48 Total area of shaded bit 401. 92 – 100. 48 = 301. 44

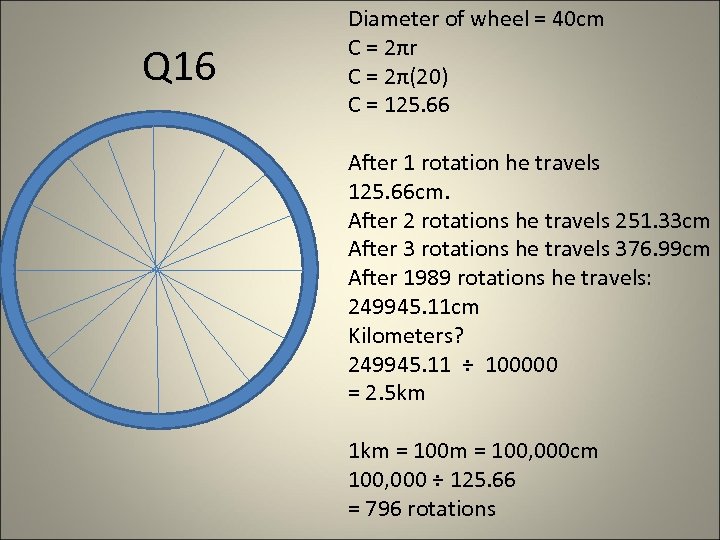Q 16 Diameter of wheel = 40 cm C = 2πr C = 2π(20) C = 125. 66 After 1 rotation he travels 125. 66 cm. After 2 rotations he travels 251. 33 cm After 3 rotations he travels 376. 99 cm After 1989 rotations he travels: 249945. 11 cm Kilometers? 249945. 11 ÷ 100000 = 2. 5 km 1 km = 100, 000 cm 100, 000 ÷ 125. 66 = 796 rotations

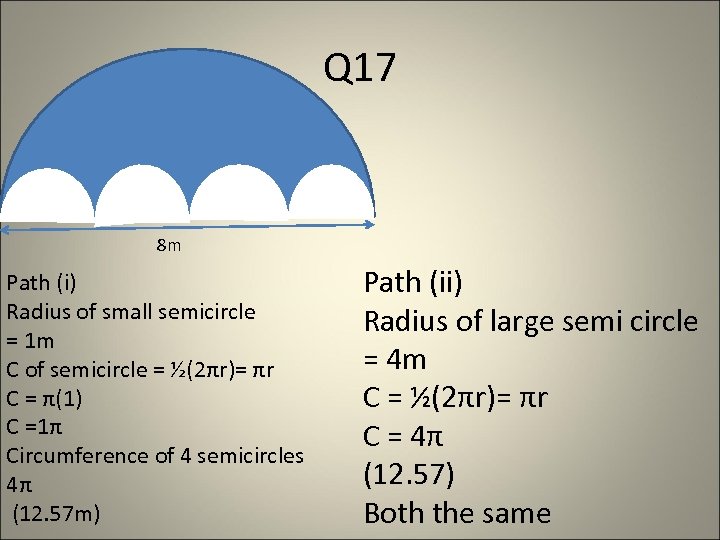Q 17 8 m Path (i) Radius of small semicircle = 1 m C of semicircle = ½(2πr)= πr C = π(1) C =1π Circumference of 4 semicircles 4π (12. 57 m) Path (ii) Radius of large semi circle = 4 m C = ½(2πr)= πr C = 4π (12. 57) Both the same

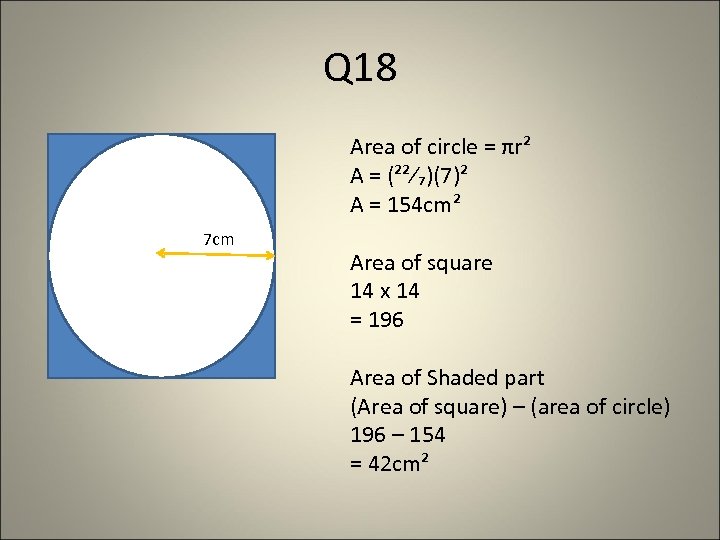Q 18 Area of circle = πr² A = (²²⁄₇)(7)² A = 154 cm² 7 cm Area of square 14 x 14 = 196 Area of Shaded part (Area of square) – (area of circle) 196 – 154 = 42 cm²

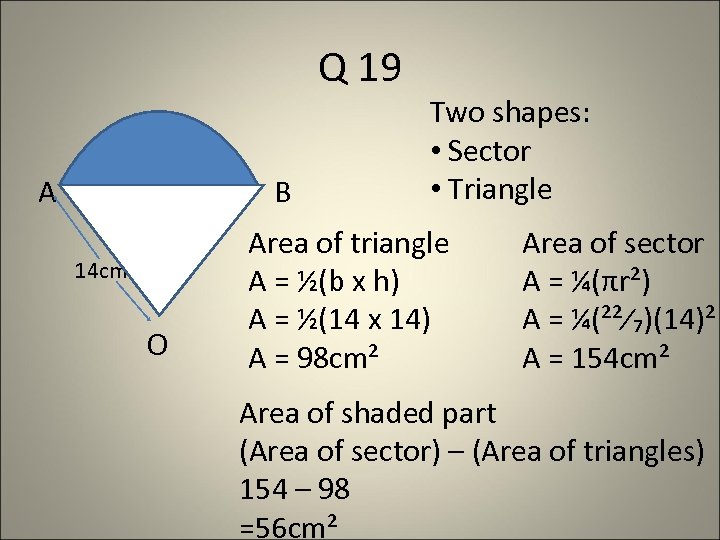Q 19 A B 14 cm O Two shapes: • Sector • Triangle Area of triangle A = ½(b x h) A = ½(14 x 14) A = 98 cm² Area of sector A = ¼(πr²) A = ¼(²²⁄₇)(14)² A = 154 cm² Area of shaded part (Area of sector) – (Area of triangles) 154 – 98 =56 cm²

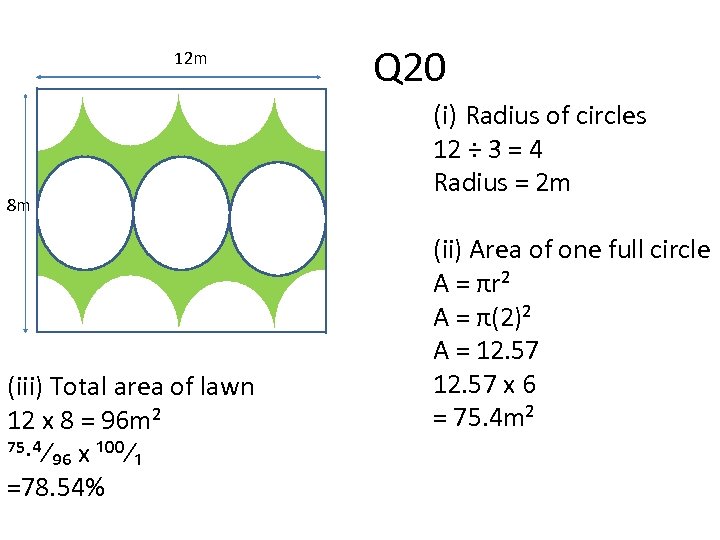12 m 8 m (iii) Total area of lawn 12 x 8 = 96 m² ⁷⁵·⁴⁄₉₆ x ¹⁰⁰⁄₁ =78. 54% Q 20 (i) Radius of circles 12 ÷ 3 = 4 Radius = 2 m (ii) Area of one full circle A = πr² A = π(2)² A = 12. 57 x 6 = 75. 4 m²

The net of a 3 D shape 8 cm 14 cm 10 cm 15 cm 6 cm 16 cm 6 cm 4 cm 7 cm 15 cm

Sample Question 2011 Junior Cert

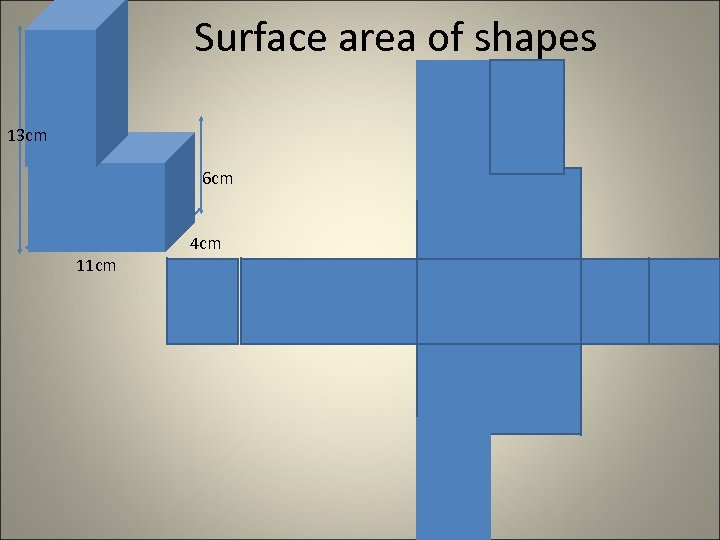Surface area of shapes 13 cm 6 cm 11 cm 4 cm

What is the logo for? ? Nintendo 64 How many faces does it have?

Volume How much space something takes up 19 cm 10 cm 9 cm For a regular solid: V=lxbxh V = 10 x 9 x 19 V = 1710 cm³

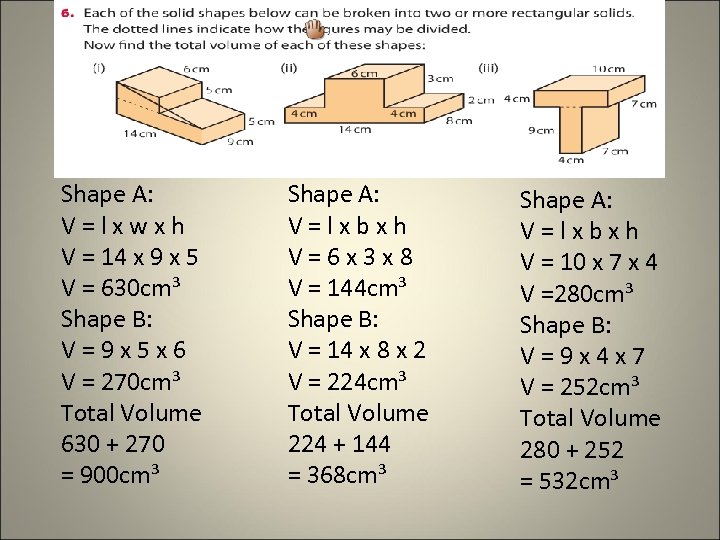Shape A: V=lxwxh V = 14 x 9 x 5 V = 630 cm³ Shape B: V=9 x 5 x 6 V = 270 cm³ Total Volume 630 + 270 = 900 cm³ Shape A: V=lxbxh V=6 x 3 x 8 V = 144 cm³ Shape B: V = 14 x 8 x 2 V = 224 cm³ Total Volume 224 + 144 = 368 cm³ Shape A: V=lxbxh V = 10 x 7 x 4 V =280 cm³ Shape B: V=9 x 4 x 7 V = 252 cm³ Total Volume 280 + 252 = 532 cm³

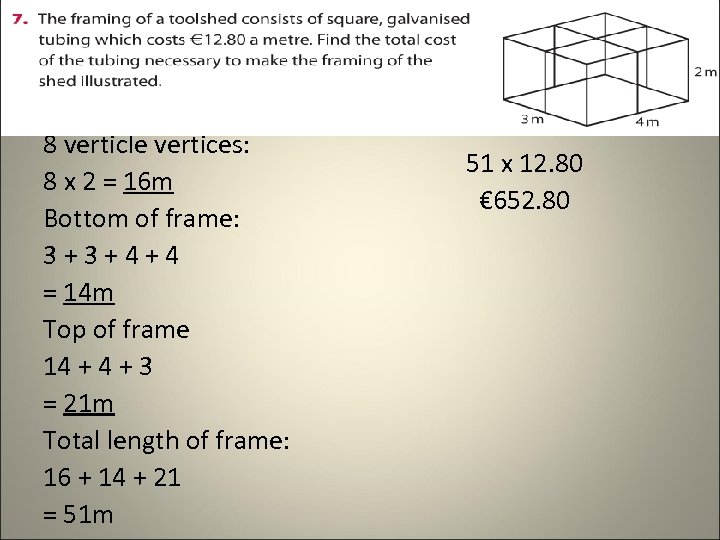8 verticle vertices: 8 x 2 = 16 m Bottom of frame: 3+3+4+4 = 14 m Top of frame 14 + 3 = 21 m Total length of frame: 16 + 14 + 21 = 51 m 51 x 12. 80 € 652. 80

V=lxwxh 120 = 8 x a x 3 120 = 24 a a = 120/24 a = 5 cm V=lxwxh 420 = 10 x 6 x b 420 = 60 a a = 420/60 a = 7 cm V=lxwxh 2240 = 14 x c x 8 2240 = 224 c c = 2240/224 c = 10 cm

(i) Height of the box h = 8 cm l = 7 cm w = x cm (ii) Volume = 84 cm V=hxlxw 84 = 8 x 7 x (x) 84 = 56 x x = ⁸⁴⁄₅₆ x = 3/2 x = 1½ Surface Area: Area = 1½ x 21 = 31½ cm² Area = 9½ x 7 = 66½ cm² Area = 8 x 7 = 56 cm² Total surface area = = 56 + 66½ + 3½ = 154 cm²

Capacity is Volume in Litres V=lxwxh V = 20 x 15 x 20 V = 6000 cm² Capacity = 6000/1000 Capacity = 6 litres V=lxwxh V = 8 x 10 x 20 V = 1600 cm² Capacity = 1600/1000 Capacity = 1. 6 litres V=lxwxh V = 30 x 15 V = 6000 cm² Capacity = 6750/1000 Capacity = 6. 75 litres

Prisms

Finding Volume of Prism 8 cm 20 cm Volume of Prism = (Area of Cross Section) x length Area of circle = πr² A = (3. 14)(8)² A = 200. 96 cm² Volume = 200. 96 x 20 V = 4019. 2 cm³

Scale Drawing http: //www. youtube. com/watch? v=HEheh 1 BH 3 4 Q

Calculating Scale On a map the distance between two towns is 4. 3 cm. If the scale is 1: 250, 000, then find the actual distance between the two towns? Scale = 1: 125, 000 4. 3 x 125, 000 = 537500 cm = 5, 375 m Distance = 5. 375 km

A diagram of a car shows the length to be 5 cm. If the actual size of the car is 2. 5 metres, find what the scale of the diagram is 2. 5 m = 250 cm Scale = 5: 250 (divide both sides by 5) = 1: 50 A house is 15 cm high in a book. Find the scale if the house is 5. 55 metres in real life. 5. 55 metres = 555 cm Scale = 15: 555 = 1: 37

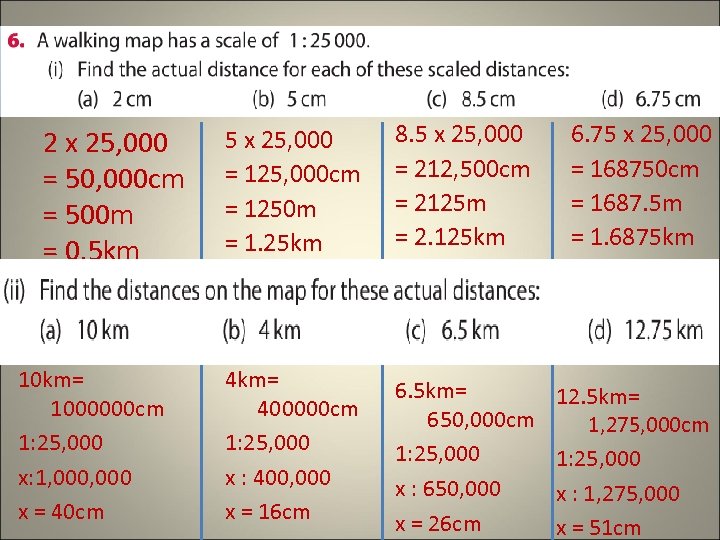2 x 25, 000 = 50, 000 cm = 500 m = 0. 5 km 10 km= 1000000 cm 1: 25, 000 x: 1, 000 x = 40 cm 5 x 25, 000 = 125, 000 cm = 1250 m = 1. 25 km 8. 5 x 25, 000 = 212, 500 cm = 2125 m = 2. 125 km 6. 75 x 25, 000 = 168750 cm = 1687. 5 m = 1. 6875 km 4 km= 400000 cm 1: 25, 000 x : 400, 000 x = 16 cm 6. 5 km= 650, 000 cm 1: 25, 000 x : 650, 000 x = 26 cm 12. 5 km= 1, 275, 000 cm 1: 25, 000 x : 1, 275, 000 x = 51 cm

Ratio = 1 : 10 (a) |AB| = 120 m = 12 cm on plan Ratio = 1 : 10 (a) |BC| = 85 m = 8. 5 cm on plan

2 km = 2000 m = 200, 000 cm 5 : 200, 000 1 : 40, 000 (divide both by 5) 30 km = 3, 000 cm 1 : 40, 000 3, 000 ÷ 40, 000 = 75 Is there another way to do this?

Q 1 Page 112 1 km = 100, 000 cm Ratio 10: 100, 000 = 1 : 10, 000 (divide both sides by 10) 10 m = 10, 000 mm Ratio 10: 10, 000 = 1 : 1, 000 (divide both sides by 10)

Scale 1: 100 5 cm = 5 x 100 = 500 cm =5 m Scale 1: 100 11 cm = 11 x 100 = 1, 100 cm =11 m Scale 1: 100 8. 5 cm = 8. 5 x 100 = 850 cm =8. 5 m Scale 1: 100 14. 8 cm = 14. 8 x 100 = 1480 cm =14. 8 m

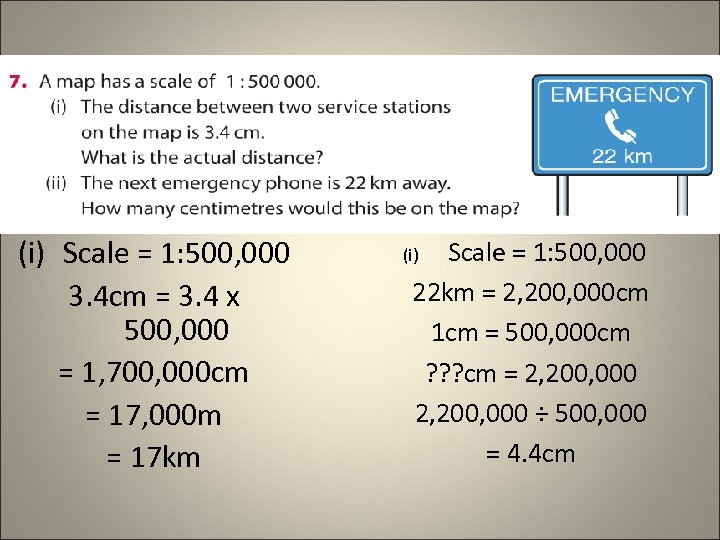(i) Scale = 1: 500, 000 3. 4 cm = 3. 4 x 500, 000 = 1, 700, 000 cm = 17, 000 m = 17 km Scale = 1: 500, 000 22 km = 2, 200, 000 cm 1 cm = 500, 000 cm ? ? ? cm = 2, 200, 000 ÷ 500, 000 = 4. 4 cm (i)

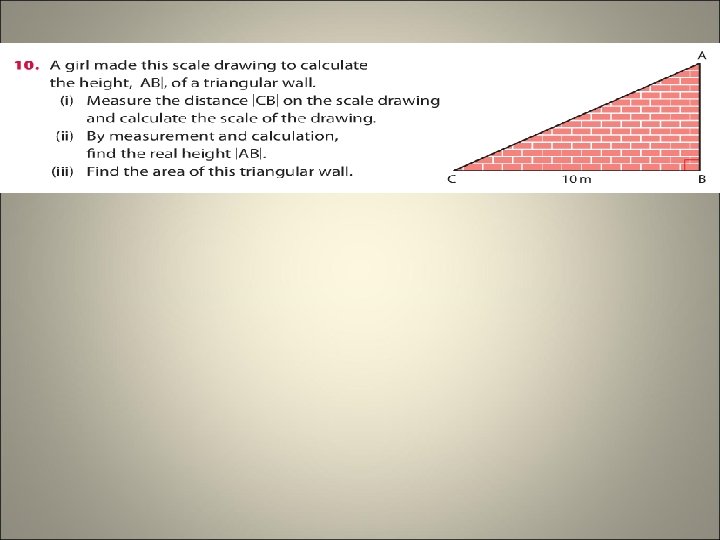
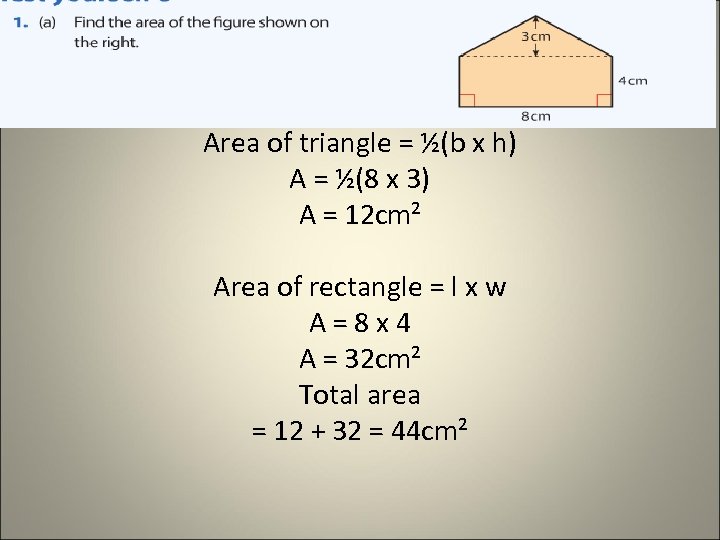Area of triangle = ½(b x h) A = ½(8 x 3) A = 12 cm² Area of rectangle = l x w A=8 x 4 A = 32 cm² Total area = 12 + 32 = 44 cm²

V=lxwxh 1320 = 20 x 12 x h 1320 = 240 h h = 5. 5 cm

V = (area of cross section) x length Area of triangle = ½(b x h) Area = ½(b x h) A = ½(6 x 8) A = 24 cm² Volume V = 24 x 4 V = 96 cm² Is there another way? Surface area: Area of triangles = 24 x 2 = 48 cm² Area of base = 4 x 6 = 24 cm² Area of back = 8 x 4 = 32 cm² Area of slant = 10 x 4 = 40 cm² Total area = 48 + 24 + 32 + 40 = 144 cm²

What fraction of a circle do we have there? = ¹²⁰⁄₃₆₀ = ⅓ Formula: A = ⅓(πr²) A = ⅓(3. 14)(6)² A =37. 68

(i) Area of a Parallelogram? A=bxh A = 10 x h? A=8 x 9 A = 72 cm² (i) Value of h A=bxh 72 = 10 x h 72 = 10 h h = 7. 2

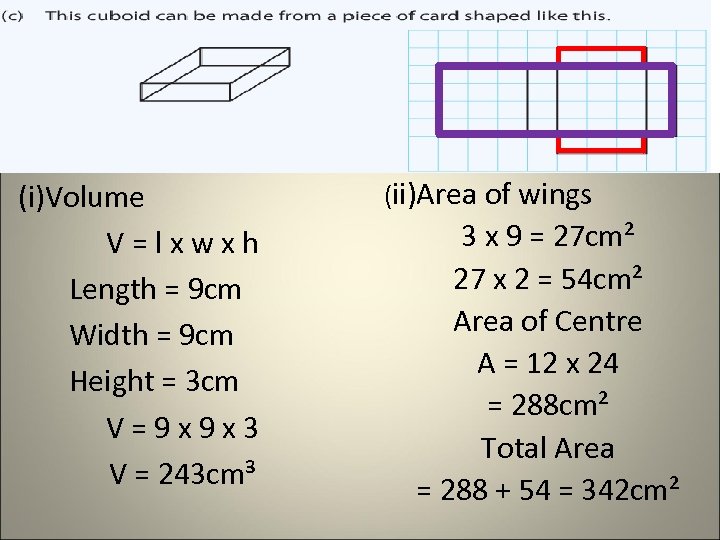(i)Volume V=lxwxh Length = 9 cm Width = 9 cm Height = 3 cm V=9 x 9 x 3 V = 243 cm³ (ii)Area of wings 3 x 9 = 27 cm² 27 x 2 = 54 cm² Area of Centre A = 12 x 24 = 288 cm² Total Area = 288 + 54 = 342 cm²

Area: Square = l x w = 8 x 8 = 64 cm² Semicircle: A = ½(πr²) A = ½(3. 14)(4)² A = 25. 12 cm² Total Area = 64 + 25. 12 = 89. 12 cm² Perimeter 3 sides of square: 8 x 3 = 24 cm Circumference of arc: A = ½(2πr) A = ½(2)(3. 14)(4) A = 12. 56 cm Total circumference 24 + 12. 56 = 36. 56 cm

(i) Scale = 1: 50 25 m = 2500 cm 1 : 50 ? ? ? : 2500 ÷ 50 = 50 cm (ii)6. 25 m = 625 cm Scale = 25 : 625 1 : 25 (divide both sides by 25)

(i) Volume of A V=lxwxh V = 3 x 2 = 18 m³ Volume of B V = area x length Area = ½(b x h) A = ½(3 x 2) = 3 cm Volume = 3 x 6 = 18 m³ (ii) S. A. of Cuboid 2(3 x 2) + 2(3 x 3) Surface Area = 42 m² S. A. of Triangular Prism 2(3) + 2(2. 5 x 6) + (6 x 3) Surface Area = 54 m²

(iii) Surface area = 54 m² Cost of 1 m² = € 24. 50 Cost of 54 cm² 24. 50 x 54 = € 1, 323