Are You In KLEINed — 4 Solitaire

Are You In. KLEINed - 4 Solitaire?

Presented by: w Matt Bach w Ryan Erickson w Angie Heimkes w Jason Gilbert w Kim Dressel

History of Peg Solitaire w Invented by French Noblemen in the 17 th Century, while imprisoned in the Bastille w The game used the Fox & Geese Board that was used by many games in Northern Europe prior to the 14 th Century

Fox and Geese Board w May have originated from Iceland w The game is 2 player w Consists of 1 black token and 13 white tokens w The Fox must capture as many geese as he can so they can’t capture him w The Geese must maneuver themselves so they can prevent the fox from escaping.

Puzzle Pegs This is a 19 th Century version of Peg Solitaire

Puzzle-Peg A 1929 version of Peg Solitaire

Jewish Version Made at Israel in 1972 with instruction printed in Hebrew. Very identical to the previous versions

Teasing Pegs This game has an alternative called French Solitaire.

Hi-Q

Felix Klein w We are modeling peg solitaire on the Klein 4 -Group named after him. w Born in Dusseldorf in 1849 w Studied at Bonn, Got Tingen, and Berlin

Fields of Work w Non-Euclidean geometry w Connections between geometry and group theory w Results in function theory

More about Felix Klein w He intended on becoming a physicist, but that changed when be became Plucker’s assistant. w After he got his doctorate in 1868, he was given the task of finishing the late Plucker’s work on line geometry w At the age of 23, he became a professor at Erlangen, and held a chair in the Math Department w In 1875, He was offered a chair at the Technische Hochschule at Munich where he taught future mathematicians like Runge and Planck.

Rules of Peg Solitaire w Rule 1: You can only move a peg in the following directions: North, South, East, and West. w Rule 2: During a move, you must jump over another peg to the corresponding empty hole. w Rule 3: To win, you must only have one peg remaining on the board

Example Game (Cross) Initial Configuration 1 st Move

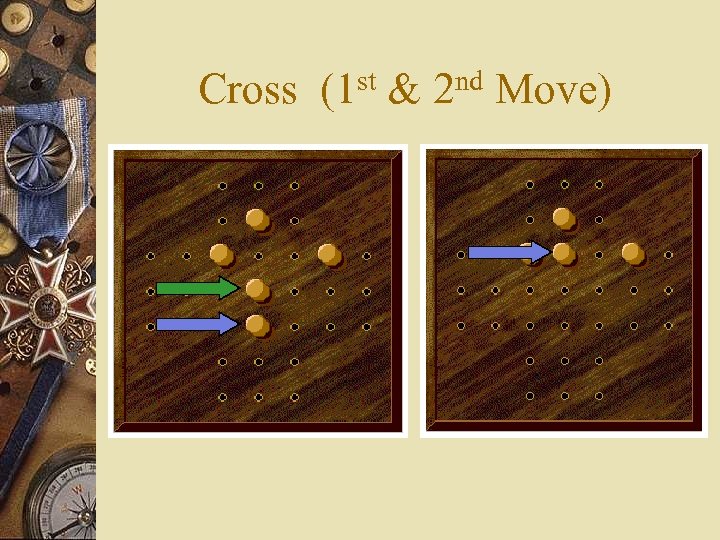Cross (1 st & 2 nd Move)

Cross (2 nd & 3 rd Move)

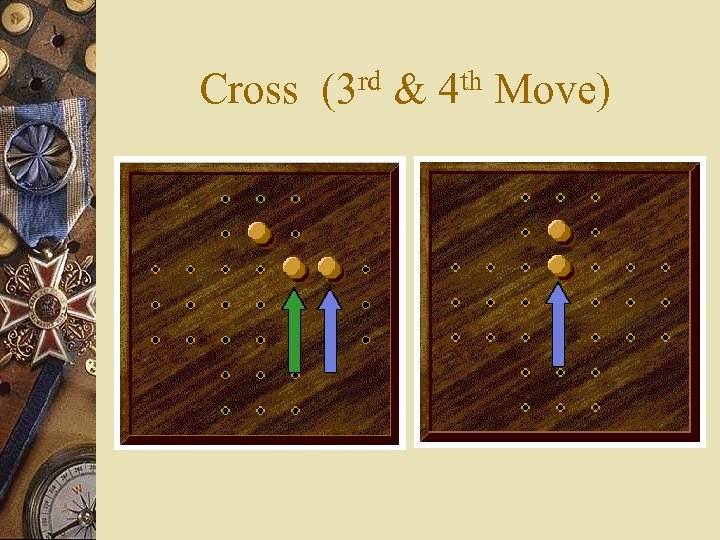Cross (3 rd & 4 th Move)

Cross (4 th & 5 th Move) You Win!!!

Other Peg Solitaire Games Arrow Diamond Double Arrow Pyramid Fireplace Standard

GROUPS Let G be a nonempty set with operation * a, b, c are elements of G e is the identity element of G G is a GROUP if it has: 1. 2. 3. 4. Binary Operation a*b G for all a, b G Associative (a*b)*c = a*(b*c) for all a, b, c G Identity a*e = e*a =a for all a G Inverses a*b = b*a = e

SPECIAL PROPERTIES w If the group has the property : a*b = b*a then the group is called ABELIAN w A group is called CYCLIC if an element a G such that G = { n Z}

KLEIN 4 GROUP It has two special properties 1. Every element is its own inverse 2. The sum of two distinct non zero elements is equal to the third element The Klein 4 Group is the direct sum of two cyclic groups.

Z Modules An integer module is similar to a vector space. In our case, contains: w Configuration Vectors w Move Vectors and contains values described by lattice points {-1, 0, 1, 2, -3} (0, 0) (1, 0) (0, 1) (– 1, 0) (0, -1)

Move Vectors w Equations are represented in the following way: w is a configuration with a peg in the (i, j)th position. w Moves are made by adding and subracting these vectors.

Module Homomorphism Properties w The mapping must satisfy these properties: 1. (a + b) = (a) + (b) 2. (ca) = c (a) w A KERNEL of a homomorphism from a group G to another group is the set: {x G| (x) = e} w The kernel of is denoted as Ker

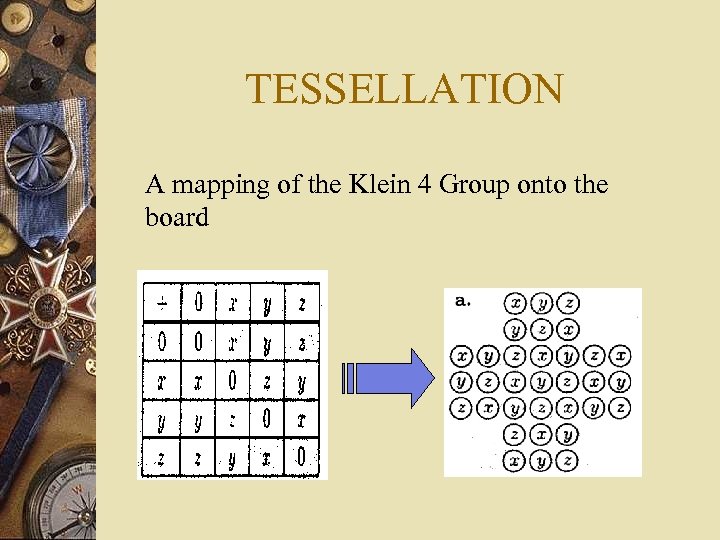TESSELLATION A mapping of the Klein 4 Group onto the board

Definition of Feasibility The dictionary defines feasibility as follows: w Can be done easily; possible without difficulty or damage; likely or probable.

Peg Solitaire Feasibility Problem Objective: 1. We want to prove whether a certain board configuration is possible. 2. We must prove there is a legal sequence that transforms one configuration into another. 3. Use the 5 Locations Thm and the Rule of Three to solve the feasibility problem.

How the Feasibility Problem Works w Given a Board B and a pair of configurations (c, c') on B, determine if the pair (c, c') is feasible.

The Solitaire Board is defined as follows: w The board is a set of integer points in a plane w C and C' are tessellations or configuration vectors of the board w C' is “ 1 – C” or the opposite of C

The Five Locations Theorem w Dr. Arie Bialostocki w Prove: If a single peg configuration is achieved, the peg must exist in one of five locations

Prerequisites w English style game board w Game begins with one peg removed from the center of the board w General rules apply

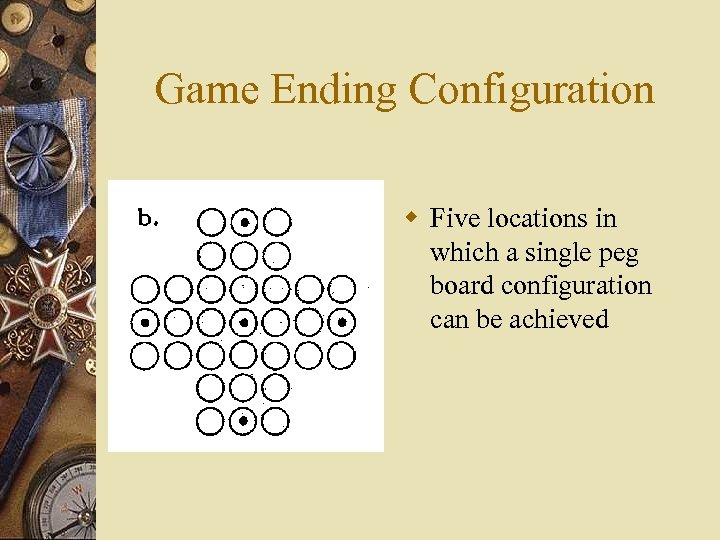Game Ending Configuration w Five locations in which a single peg board configuration can be achieved

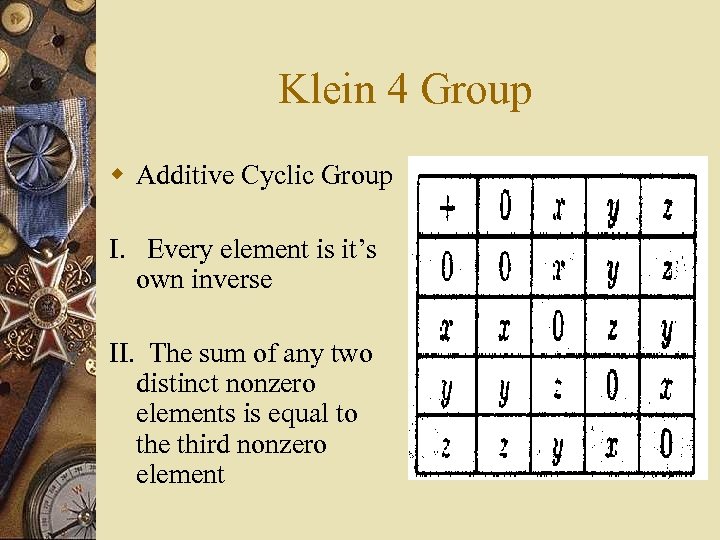Klein 4 Group w Additive Cyclic Group I. Every element is it’s own inverse II. The sum of any two distinct nonzero elements is equal to the third nonzero element

Board Tessellation w Assign x, y, z values to a 7 x 7 board starting in row 1 and column 1 w Map from left to right, top to bottom w Remove the four locations from each of the four corners to produce a board tessellation

Adding Using Tessellation w By Klein 4 properties I and II, the sum of any x + y + z = 0 w Therefore, adding up the individual pegged locations based on the tessellation, the total board value initially = y

Calculating After Move w For any move, the sum of two elements from x, y, z is replaced by the third element w According to property II of Klein 4 groups, this substitution does not affect the overall sum of the board

Peg Must Be Left In Y w Therefore, a single peg can only be left in a y location w However, because of the rules of symmetry, six of these eleven locations must be removed

Five Locations Remain w Therefore, only five locations remain and Dr. Bialostocki’s Five Locations Theorem holds.

Notion for Scoring Let is the Klein 4 - Group is the Klein Product Module Abelian group with the following properties a + a = b + = c + c = e a + b = c, a + c = b , b + c = a

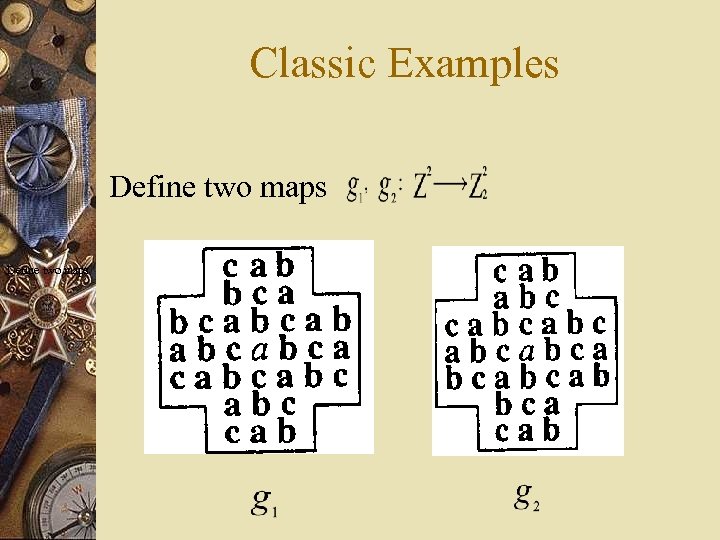Classic Examples Define two maps

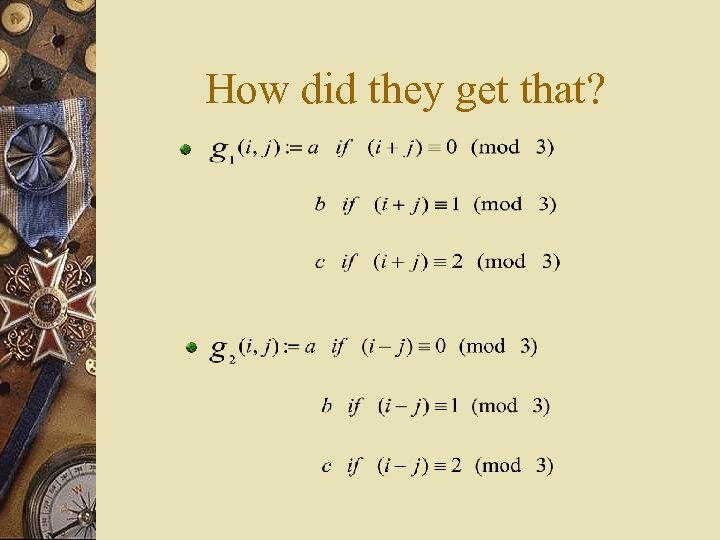How did they get that?

Game Configurations A single peg or “basis vector” is represented by the following: filled empty

Score Map (A module homomorphism- a linear like map) For any board , the score map can be defined by the following notation: As shown by the previous examples Thus the score of

An Example = board vector that has a peg in (0, 0) and is empty every where else. ( ) = 1* = 1 * (a , a) = (a , a)

The Board Score B = English 33 - board C = (B)= ( ) + (1 - ) = (a , a) + (a , a) =(a + a, a + a) =(e , e)

Note: Let We can show that For example,

Rule of Three A necessary condition for a pair of configuration (c, c ) to be feasible is that (c - c) = (e, e), namely, c - c er( ).

Proof: Suppose (c, ) is feasible. Then c = c + (c ) = [c + ] (c ) = (c) + ( ) (c )= (c) + (e, e) (c )= (c) + (e, e) (c ) - (c) = (e, e) (c - c) = (e, e)

Proposition 2 Let B be any board. A necessary condition for the configurations pair (c, ) to be feasible, with = 1 - c the complement of c, is that the board score is (B) = (e, e).

Proof: Assume(c, ) is feasible. = 1 - c By the Rule of Three c - Ker( ), i. e. ( c - ) = (e, e) ( c) - ( ) = (e, e) ( c) = (e, e) + ( ) ( c) = ( )

Proof Continued: However: (B) = ( c) + ( ) (B) = ( c) + ( c) (B) = (e, e)

Conclusion w By using the Five Locations Theorem, and the Rule of Three, we have shown how it is possible to come up with the winning combinations in peg solitaire, and have shown why they work

Possible Questions w Can this model be applied to other games? w How many solutions are there to the Peg Solitaire Game? w Is there a general algorithm for solving central solitaire?

References w Dr. Steve Deckelman w “An Application of Elementary Group Theory to Central Solitaire” – by Arie Bialostocki w “Solitaire Lattices” – by Antoine Deza, Shmuel Onn w Websites – http: //bio. rpi. edu/MS 99/Whitney. W/advance/klein. ktm – http: //library. thinkquest. org/22584/temh 3043. htm – http: //physics. rug. ac. be/fysica/Geschiedenis/mathematicians/Klei n. F. html – http: //www. ahs. uwaterloo. ca/~museum/vexhibit/puzzles/solitaire/ solitaire. html