20054bd52a0bdf233e8d34f449012990.ppt
- Количество слайдов: 54

Aquery: A DATABASE SYSTEM FOR ORDER Dennis Shasha, joint work with Alberto Lerner {lerner, shasha}@cs. nyu. edu

Motivation The need for ordered data • Queries in finance, signal processing etc. depend on order. • SQL 99 has extensions but they are clumsy.

Moving Averages is algorithmically linear but… Sales(month, total) SELECT t 1. month+1 AS forecast. Month, (t 1. total+ t 2. total + t 3. total)/3 AS 3 Month. Moving. Average FROM Sales AS t 1, Sales AS t 2, Sales AS t 3 WHERE t 1. month = t 2. month - 1 AND t 1. month = t 3. month – 2 Can optimizer make a 3 -way (in general, n-way) join linear Mining Ref: Datatime? and Statistical Analysis Using SQL Trueblood and Lovett Apress, 2001

Moving Averages in SQL 99 is awkward Sales(month, total) Alberto, please put in SQL 99

Choose query from Jennifer Alberto, I suggest query 2 because that may be hard in sql 99.

Motivation Problems Extending SQL with Order • Queries are hard to read • Cost of execution is often non-linear (would not pass basic algorithms course) • Few operators preserve order, so optimization hard.

Idea • Whatever can be done on a table can be done on an ordered table (arrable). Not vice versa. • Aquery – query language on arrables; operations on columns. • Upward compatible from SQL 92. • Optimization ideas are new, but natural.

SQL + Order Moving Averages Sales(month, total) avgs: vector-to-vector function, order-dependant and size-preserving SELECT month, avgs(8, total) FROM Sales order ASSUMING ORDER month to be used on vectorto-vector functions Execution (Sales is an arrable): 1. FROM clause – enforces the order in ASSUMING clause 2. SELECT clause – for each month yields the moving average (window size 8) ending at that month.

SQL + Order Top N Employee(ID, salary) first: vector-to-vector function, order-dependant and non size-preserving SELECT first(N, salary) FROM Employee ASSUMING ORDER Salary Execution: 1. FROM clause – orders arrable by Salary 2. SELECT clause – applies first() to the ‘salary’ vector, yielding first N values of that vector given the order. Could get the top earning IDs by saying first(N, ID).
![SQL + Order Vector-to-Vector Functions sizepreserving non sizepreserving prev, next, $, [] orderdependant non SQL + Order Vector-to-Vector Functions sizepreserving non sizepreserving prev, next, $, [] orderdependant non](https://present5.com/presentation/20054bd52a0bdf233e8d34f449012990/image-10.jpg)
SQL + Order Vector-to-Vector Functions sizepreserving non sizepreserving prev, next, $, [] orderdependant non orderdependant avgs(*), prds(*), sums(*), deltas(*), ratios(*), reverse, … drop, first, last rank, tile min, max, avg, count
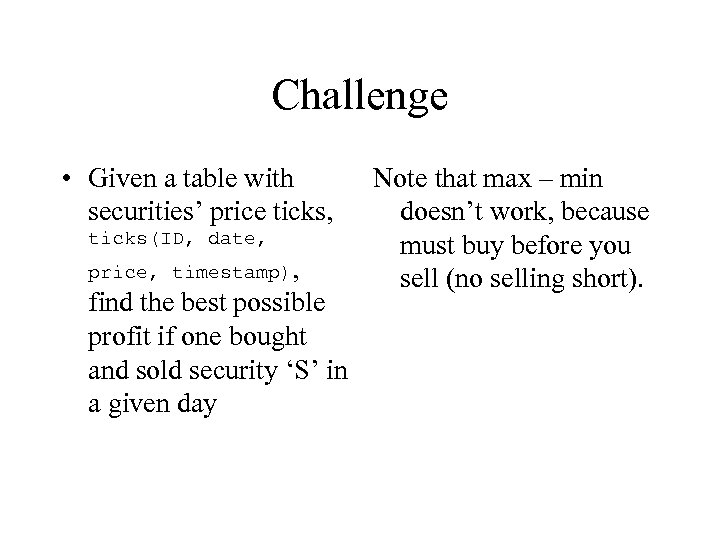
Challenge • Given a table with securities’ price ticks, ticks(ID, date, price, timestamp), find the best possible profit if one bought and sold security ‘S’ in a given day Note that max – min doesn’t work, because must buy before you sell (no selling short).

Complex queries: Best spread In a given day, what would be the maximum difference between a buying and selling point of each security? Ticks(ID, price, trade. Date, timestamp, …) max best SELECT ID, max(price – mins(price)) spread FROM Ticks ASSUMING ORDER timestamp min WHERE trade. Date = ‘ 99/99/99’ GROUP BY ID running min Execution: 1. For each security, compute the running minimum vector for price and then subtract from the price vector itself; result is a vector of spreads. 2. Note that max – min would overstate spread.

Best-profit query SELECT max(price – mins(price)) FROM ticks ASSUMING ORDER timestamp WHERE day = ‘ 12/09/2002’ AND ID = ‘S’ price mins - 15 19 13 7 4 5 4 7 12 2 15 15 13 7 4 4 4 0 4 0 0 0 1 0 3 8 2
![Best-profit query comparison [AQuery] SELECT max(price–mins(price)) FROM ticks ASSUMING timestamp WHERE ID=“x” AND trade. Best-profit query comparison [AQuery] SELECT max(price–mins(price)) FROM ticks ASSUMING timestamp WHERE ID=“x” AND trade.](https://present5.com/presentation/20054bd52a0bdf233e8d34f449012990/image-14.jpg)
Best-profit query comparison [AQuery] SELECT max(price–mins(price)) FROM ticks ASSUMING timestamp WHERE ID=“x” AND trade. Date='99/99/99' [SQL: 1999] SELECT max(rdif) FROM (SELECT ID, trade. Date, price - min(price) OVER (PARTITION BY ID ORDER BY timestamp ROWS UNBOUNDED PRECEDING) AS rdif FROM Ticks ) AS t 1 WHERE ID=“x” AND trade. Date='99/99/99'

Complex queries: Crossing averages part I When does the 21 -day average cross the 5 -month average? Market(ID, close. Price, trade. Date, …) Traded. Stocks(ID, Exchange, …) INSERT INTO temp FROM SELECT ID, trade. Date, avgs(21 days, close. Price) AS a 21, avgs(5 months, close. Price) AS a 5, prev(avgs(21 days, close. Price)) AS pa 21, prev(avgs(5 months, close. Price)) AS pa 5 FROM Traded. Stocks NATURAL JOIN Market ASSUMING ORDER trade. Date GROUP BY ID

Complex queries: Crossing averages part uses non 1 NF Execution: 1. FROM clause – order-preserving join 2. GROUP BY clause – groups are defined based on the value of the Id column 3. SELECT clause – functions are applied; non-grouped columns become vector fields that target cardinality is so met. Violates first normal form Vector field groups in ID and non-grouped column grouped ID and non-grouped column two columns with the same cardinality

Complex queries: Crossing averages part II Get the result from the resulting non first normal form relation temp SELECT ID, trade. Date FROM flatten(temp) WHERE a 21 > a 5 AND pa 21 <= pa 5 Execution: 1. FROM clause – flatten transforms temp into a first normal form relation (for row r, every vector field in r MUST have the same cardinality). Could have been placed at end of previous query. 2. Standard query processing after that.

SQL + Order Related Work: Research • SEQUIN – Seshadri et al. – Sequences are first-class objects – Difficult to mix tables and sequences. • SRQL – Ramakrishnan et al. – Elegant algebra and language – No work on transformations. • SQL-TS – Sadri et al. – Language for finding patterns in sequence – But: Not everything is a pattern!

SQL + Order Related Works: Products • RISQL – Red Brick – Some vector-to-vector, order-dependent, sizepreserving functions – Low-hanging fruit approach to language design. • Analysis Functions – Oracle 9 i – Quite complete set of vector-to-vector functions – But: Can only be used in the select clause; poor optimization (our preliminary study) • KSQL – Kx Systems – Arrable extension to SQL but syntactically incompatible. – No cost-based optimization.

Order-related optimization techniques • Starburst’s “glue” (Lohman, 88) and Exodus/Volcano “Enforcers” (Graefe and Mc. Keena, 93) • DB 2 Order optimization (Simmen et al. , 96) • Top-k query optimization (Carey and Kossman, 97) • Hash-based order-preserving join (Claussen et al. , 01) • Temporal query optimization addressing order and duplicates (Slivinskas et al. , 01)
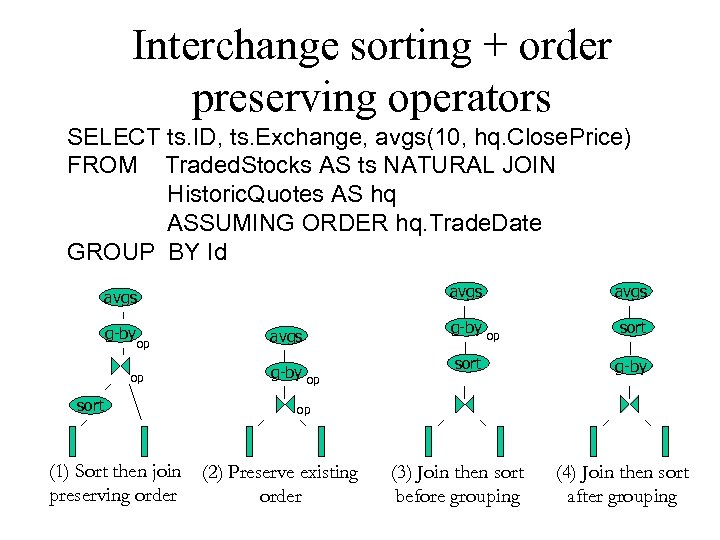
Interchange sorting + order preserving operators SELECT ts. ID, ts. Exchange, avgs(10, hq. Close. Price) FROM Traded. Stocks AS ts NATURAL JOIN Historic. Quotes AS hq ASSUMING ORDER hq. Trade. Date GROUP BY Id avgs g-by op op sort (1) Sort then join preserving order avgs g-by op sort g-by op (2) Preserve existing order (3) Join then sort before grouping (4) Join then sort after grouping

Transformations Early sorting + order preserving operators
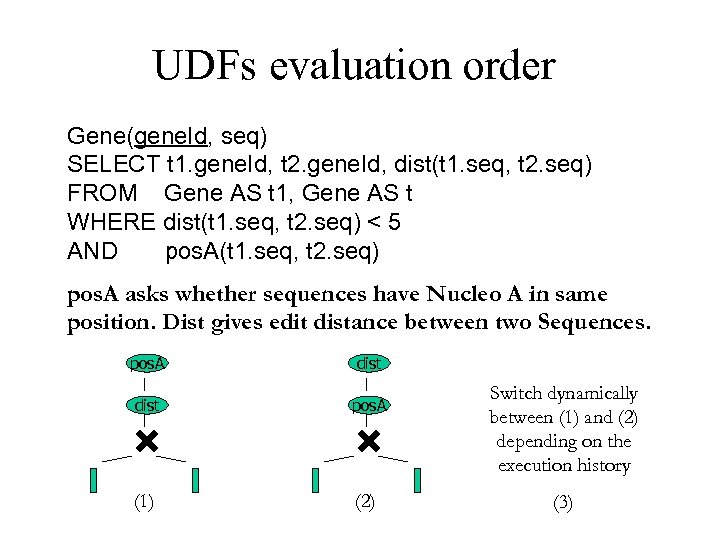
UDFs evaluation order Gene(gene. Id, seq) SELECT t 1. gene. Id, t 2. gene. Id, dist(t 1. seq, t 2. seq) FROM Gene AS t 1, Gene AS t WHERE dist(t 1. seq, t 2. seq) < 5 AND pos. A(t 1. seq, t 2. seq) pos. A asks whether sequences have Nucleo A in same position. Dist gives edit distance between two Sequences. pos. A dist pos. A (1) (2) Switch dynamically between (1) and (2) depending on the execution history (3)

Transformations UDFs Evaluation Order

• Transformations Building Blocks Order optimization – Simmens et al. `96 – push-down sorts over joins, and combining and avoiding sorts • Order preserving operators – KSQL – joins on vector – Claussen et al. `00 – OP hash-based join • Push-down aggregating functions – Chaudhuri and Shim `94, Yan and Larson `94 – evaluate aggregation before joins • UDF evaluation – Hellerstein and Stonebraker ’ 93 – evaluate UDF according to its ((output/input) – 1)/cost per tuple – Porto et al. `00 – take correlation into account

Original Query last(price) SELECT last(price) FROM ticks t, base b ASSUMING ORDER name, timestamp WHERE t. ID=b. ID AND name=“x” Name=“x” sort name, timesamp ID ticks base

Last price for a name query • The sort on name can be eliminated because there will be only one name • Then, push sort – sort. A(r 1 r 2) A sort. A(r 1) – sort. A(r) A r lop last(price) sort name, timesamp ID r 2 ticks Name=“x” base

Last price for a name query price • The projection is carrying an implicit selection: last(price) = price[n], where n is the last index of the price array – f(r. col[i])(r) order(r) f(r. col)( pos()=i(r)) pos()=last last(price) lop ID ticks Name=“x” base

Last price for a name query • But why join the entire relation if we are only using the last tuple? • Can we somehow push the last selection down the join? price pos()=last lop ID ticks Name=“x” base

Last price for a name query • We can take the last position of each ID on ticks to reduce cardinality, but we need to group by ticks. ID first • But trading a join for a group by is usually a good deal? ! • One more step: make this an “edge by” price safety lop ID pos()=last Gby. ID ticks Name=“x” base

The “edgeby” operator • The pattern edge condition(Gby(r)) can be efficiently implemented without grouping the whole arrable • An edgeby is a kind of scan that take as parameters the grouping column(s), the direction to scan, a position, and if that position is the last (scan up to) or the first one the group (scan from this on). • In the previous example, to find the last rows for each ID in ticks one would use, respectively, `ID, ' `backwards, ' ` 1, ' and 'up to. '

Conclusion • Arrable-based approach to ordered databases may be scary – dependency on order, vector-to-vector functions – but it’s expressive and fast. • SQL extension that includes order is possible and reasonably simple. • Optimization possibilities are vast.

Streaming • Aquery has no special facilities for streaming data, but it is expressive enough. • Idea for streaming data is to split the tables into tables that are indexed with old data and a buffer table with recent data. • Optimizer works over both transparently.

Arrables’ Shape Properties • • The cardinality of an arrable’s array-columns must be the same An arrable’s tuple can contain single or arrayvalued column values. – – – A 1 NF arrable contains only single values A flatten-able ¬ 1 NF arrable may contain array-valued columns, but they have the same cardinality A non-flatten-albe ¬ 1 NF arrable is one that is not in the previous categories
![Arrables Primitives • Single-value indexing r[k] retrieves the tuple formed by the k-th position Arrables Primitives • Single-value indexing r[k] retrieves the tuple formed by the k-th position](https://present5.com/presentation/20054bd52a0bdf233e8d34f449012990/image-35.jpg)
Arrables Primitives • Single-value indexing r[k] retrieves the tuple formed by the k-th position value of each of the arrables arraycolumns • Multi-value indexing r[k 1 k 2 … kn] is similar to forming an arrable by insertion of r[k 1], r[k 2], …, r[kn]

Array-columns Expressions • Expressions in AQuery are column-oriented, as opposed to row-oriented price result x > scalar = T y F z T price prev(price) result x = y x y-x z y z-y
![Built-in functions • prevv[i] = null, if i=0 or v[i-1], for 0<i |v|-1 • Built-in functions • prevv[i] = null, if i=0 or v[i-1], for 0<i |v|-1 •](https://present5.com/presentation/20054bd52a0bdf233e8d34f449012990/image-37.jpg)
Built-in functions • prevv[i] = null, if i=0 or v[i-1], for 0<i |v|-1 • firstv, n[i] = v[i], for 0 i<n • minsv[i] = v[i], if i=0 or min(v[i], mins[i-1]), for 0<i |v|-1 • indexbv[i] = i such that bv[i] is true

Each modifier • Built-in functions are applied over arraycolumns • The each keyword makes the function application occur in each tuple level

Group and flatten operations • An arrable can be grouped over a grouping expression that assigns a group value to each row. The net effect is to nest an 1 NF arrable into a flatten-able ¬ 1 F one • The flatten operation undoes the operation • But there are data-ordering issues!

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING Arrables mentioned in the FROM clause are combined using cartesian product. This is operation is orderoblivious

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING The ASSUMING ORDER is enforced. From this point on any order-dependent expression can be used, regardless of the clause.

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING The WHERE expression is executed. It must generate a boolean vector that maps each row of the current arrable to true or false. The false rows are eliminated and the resulting arrable is passed along.

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING The GROUP BY expression is computed. It must map each tuple to a group. The resulting arrable has as many rows as there are groups. The columns that did not participate on the grouping expression now have array -valued values

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING The HAVING clause expression must result in a boolean vector that maps each group, i. e, row, to a boolean value. The rows that map to false are excluded.

AQuery syntax and execution • It’s just SQL, really. But column-oriented. SELECT FROM ASSUMING ORDER WHERE GROUP BY HAVING Finally, each expression on the SELECT clause is executed, generating a new array-column. The resulting arrable is achieved by “zipping” these arrays side-byside.

Translating queries into Operations SELECT ID, index(flags=‘FIN’)index(flags=‘ACK’) FROM netmgmt ASSUMING ORDER timestamp GROUP BY ID each Gby sort netmgmt Orderpreserving portion of the plan

Non- and Order-preserving Variations • Operators may or may not be required to be preserve order, depending on their location. • For instance: – a group by based on hashing is an implementation of a non-order preserving group-by – A nested-loops join is an implementation of a left-order preserving join • There are performance implications in preserving or not order
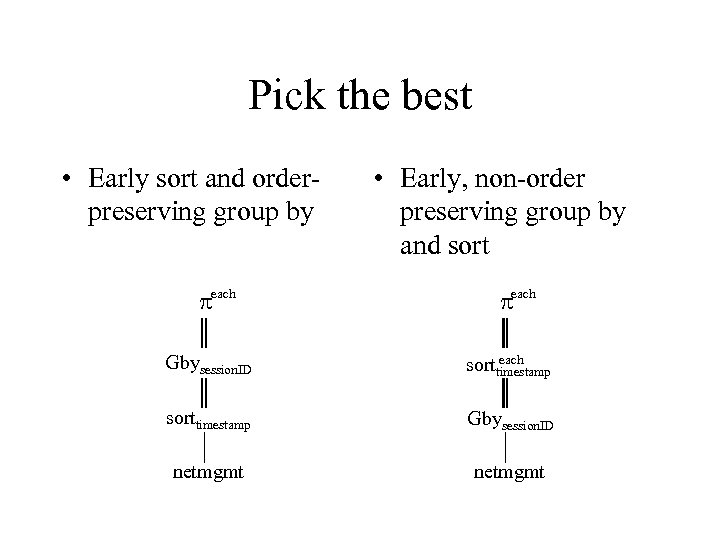
Pick the best • Early sort and orderpreserving group by each • Early, non-order preserving group by and sort each Gbysession. ID each sorttimestamp Gbysession. ID netmgmt

AQuery Optimization • Optimization is cost based • The main strategies are: – Define the extent of the order-preserving region of the plan, considering (correctness, obviously, and) the performance of variation of operators – Apply efficient implementations of patterns of operators • There are generic techniques yet each query category presents unique opportunities and challenges • Equivalence rules between operators can be used in the process

Order Equivalence • Let Order(r) return the attributes that the arrable r is “ordered by. ” • Two arrables r 1 and r 2 are order-equivalent with respect to the list of attributes A, denoted r 1 A r 2 if A is a prefix of Order(r 1) and of Order(r 2), and some permutation of r 1 is identical to r 2 • We denote by r 1 {} r 2 the case where r 1 and r 2 are multiset-equivalent (i. e. they contain the same setof tuples and for each tuple in the set, they contain the same number of instances of that tuple).

Sort Elimination • Often sort can be eliminated or can be done over less fields – sort. A(r) A r if A is prefix of Order(r) – sort. A • B(r) A • B sort’A(r) if B is prefix of Order(r) and sort’ is stable – sort. A(sort. B(r)) A • B sort. A if A B is a valid functional dependency – sort. A(sort. B(r)) A • B sort. A • (B-A) (r) – oper-path(sort(r)) {} oper-path(r) if oper-path has no order-dependent operation

Conclusion • Arrables offer a simple way to express order -based predicates and expressions • Queries tend to be lucid, concise and, consequently, order idioms stand out • Optimization naturally extend the know corpus of rules • New possibility of operator implementing algorithm that take order into consideration

Order preserving joins select lineitem. orderid, avgs(10, lineitem. qty), lineitem. lineid from order, lineitem assuming order lineid where order. date > 45 and order. date < 55 and lineitem. orderid = orderid • Basic strategy 1: restrict based on date. Create hash on order. Run through lineitem, performing the join and pulling out the qty. • Basic strategy 2: Arrange for lineitem. orderid to be an index into order. Then restrict order based on date giving a bit vector. The bit vector, indexed by lineitem. orderid, gives the relevant lineitem rows. The relevant order rows are then fetched using the surviving lineitem. orderid. Strategy 2 is often 3 -10 times faster.
20054bd52a0bdf233e8d34f449012990.ppt