45a6ab039df4860df405d9c83594f81e.ppt
- Количество слайдов: 47

Applying Pruning Techniques to Single. Class Emerging Substring Mining Speaker: Sarah Chan Supervisor: Dr. B. C. M. Kao M. Phil. Probation Talk CSIS DB Seminar Aug 30, 2002

Presentation Outline § § Introduction The single-class ES mining problem Data structure: merged suffix tree Algorithms: baseline, s-pruning, g-pruning, -pruning § Performance evaluation § Conclusions l

Introduction § Emerging Substrings (ESs) • A new type of KDD patterns • Substrings whose supports (or frequencies) increase significantly from one class to another (measured by a growth rate) • Motivation: Emerging Patterns (EPs) by Dong and Li • Jumping Emerging Substrings (JESs) as a specialization of ESs Ø Substrings which can only be found in one class but not others

Introduction § Emerging Substrings (ESs) • Usefulness Capture sharp contrasts between datasets, or trends over time Ø Provide knowledge for building sequence classifiers Ø • Applications (virtually endless) Ø Language identification, purchase behavior analysis, financial data analysis, bioinformatics, melody track selection, web-log mining, content-based e-mail processing systems, …

Introduction § Mining ESs • Brute-force approach To enumerate all possible substrings in the database, find their support counts in each class, and check growth rate Ø But a huge sequence database contains millions of sequences (Gen. Bank has 15 million sequences in 2001), and Ø No. of substrings in a sequence increases exponentially with sequence length (A typical human genome has 3 billion characters) Too many candidates Expensive in terms of time ( O(|D|2 n 3) ) and memory Ø Other shortcomings: repeated substrings, common substrings, … (Please refer to [seminar 020201]) Ø

Introduction § Mining ESs • An Apriori-like approach Ø Ø Ø E. g. if both abcd & bcde are frequent in D, generate candidate abcde Find frequent substrings and check growth rate Still requires many database scans A candidate may not be contained in any sequence in D Apriori property does not hold for ESs: abcde can be an ES even if both abcd & bcde are not • We need algorithms which are more efficient and which allow us to filter out ES candidates

Introduction § Mining ESs • Our approach: A suffix tree-based framework Ø Ø Ø A compact way of storing all substrings, with support counters maintained Deal with suffixes (not substrings) of sequences Do not consider substrings not existing in the database Time complexity: O( lg(| |) |D| n 2 ) Techniques for pruning of ES candidates can be easily applied

Basic Definitions § Sequence • An ordered set of symbols over an alphabet § Class • In a sequence database, each sequence i has a class label Ci C = the set of all class labels • does not belong to Ck belongs to Ck’ § Dataset • If database D is associated with m class labels, we can partition D into m datasets, such that all sequences in dataset Di have class label Ci • Dk Dk’

Basic Definitions § Count and support of string s in dataset D • count. D(s) = no. of sequences in D that contain s • supp. D(s) = count. D(s) / |D| § Growth rate of string s from D 1 to D 2 • growth. Rate. D 1→D 2(s) = supp. D 2(s) / supp. D 1(s) growth rate = 0 if supp. D 1(s) = 0 Ø growth rate = ∞ if supp. D 1(s) = 0 and supp. D 2(s) > 0 Ø

ES and JES § Emerging Substring (ES) • Given s and g, a string s is an ES from Dk’ to Dk (or s is an ES of Ck) if these hold: support condition: supp. Dk(s) ≥ s growth rate condition: growth. Rate. Dk’→Dk(s) ≥ g § Jumping Emerging Substring (JES) • It is an ES with ∞ growth rate • JES of Ck: supp. Dk’(s) = 0 and supp. Dk(s) > 0

ES and JES § Example Class C 1 abcd bd a c Class C 2 abd bc cd b With g = 1. 5 ESs from D 2 to D 1 : a, abc, bcd, abcd ESs from D 1 to D 2 : b, abd

ES and JES § Example Class C 1 abcd bd a c Class C 2 abd bc cd b With g = 1. 5 ESs from D 2 to D 1 : a, abc, bcd, abcd ESs from D 1 to D 2 : b, abd growth. Rate. D 1→D 2(b) = (3/4) / (2/4) = 1. 5

ES and JES § Example Class C 1 abcd bd a c Class C 2 abd bc cd b With g = 1. 5 ESs from D 2 to D 1 : a, abc, bcd, abcd ESs from D 1 to D 2 : b, abd JESs are underlined

The ES Mining Problem § The ES mining problem • Given a database D, the set C of all class labels, a support threshold s and a growth rate threshold g, to discover the set of all ESs for each class Cj C § The single-class ES mining problem • A target class Ck is specified and our goal is to discover the set of all ESs of Ck • Ck’ : opponent class

Merged Suffix Tree § Suffix tree • Represent all the substrings of a length-n sequence in O(n) space § Merged suffix tree • Represent all the substrings of all sequences in a dataset Dk in O(|Dk| n) space • Each node has a support counter for each dataset • Each node is associated with a substring and related to one or more substrings • Each edge is denoted as an index range [istart, iend) Ø E. g. if = abcd, then [1, 3) = ab
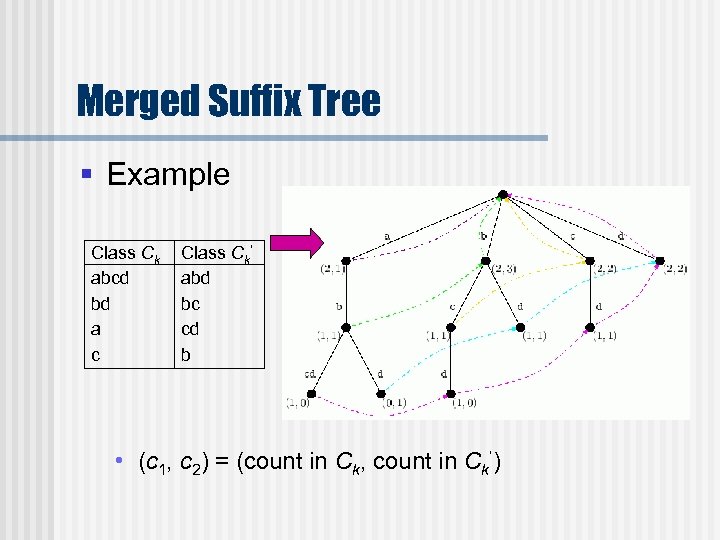
Merged Suffix Tree § Example Class Ck abcd bd a c Class Ck’ abd bc cd b A • (c 1, c 2) = (count in Ck, count in Ck’)
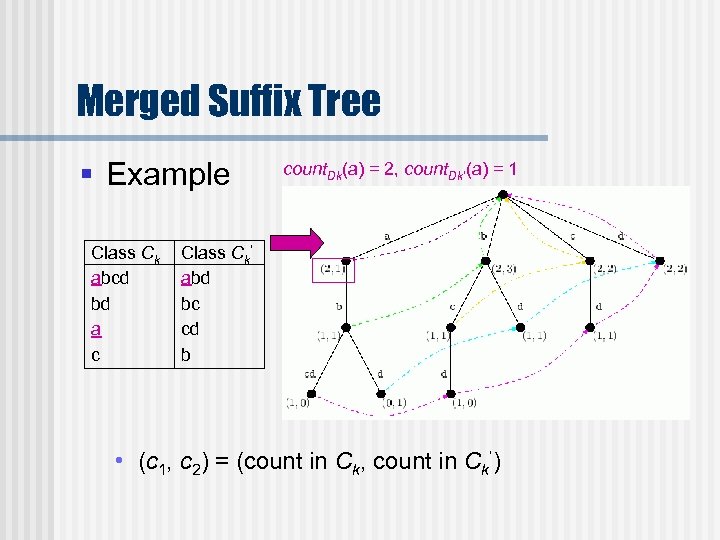
Merged Suffix Tree § Example Class Ck abcd bd a c Class Ck’ abd bc cd b count. Dk(a) = 2, count. Dk’(a) = 1 A • (c 1, c 2) = (count in Ck, count in Ck’)
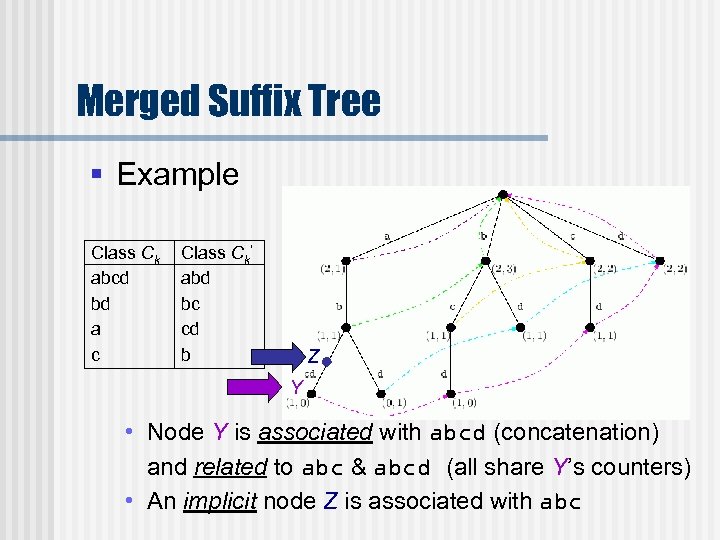
Merged Suffix Tree § Example Class Ck abcd bd a c Class Ck’ abd bc cd b Z Y • Node Y is associated with abcd (concatenation) and related to abc & abcd (all share Y’s counters) • An implicit node Z is associated with abc

Algorithms § The baseline algorithm • Consists of 3 phases § Three pruning techniques • Support threshold pruning (s-pruning algorithm) • Growth rate threshold pruning (g-pruning algorithm) • Length threshold pruning (l-pruning algorithm)

Baseline Algorithm 1. Construction Phase (C-Phase) • A merged tree MT is built from all the sequences of the target class Ck – each suffix sj of each sequence is matched against substrings in the tree Update c 1 counter for substrings contained in sj (but a sequence should not contribute twice to the same counter) Ø Explicitize implicit nodes when necessary Ø When a mismatch occurs, add a new edge and a new leaf to represent the unmatched part of sj Ø
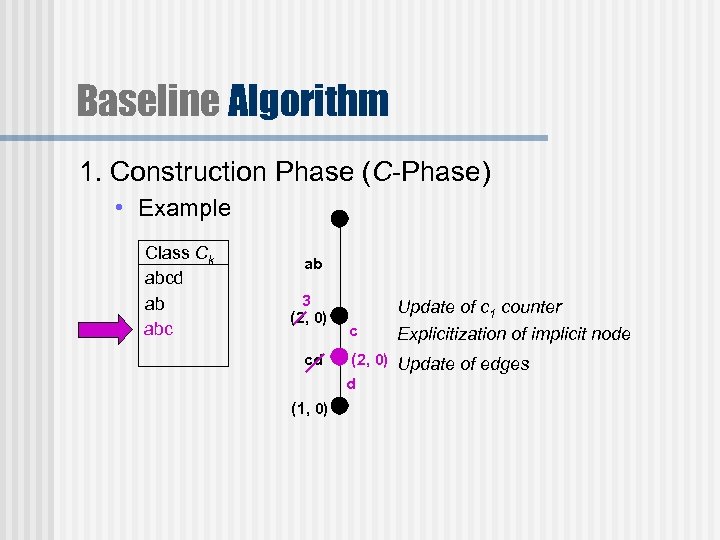
Baseline Algorithm 1. Construction Phase (C-Phase) • Example Class Ck abcd ab abc ab 3 (2, 0) cd (1, 0) c Update of c 1 counter Explicitization of implicit node (2, 0) Update of edges d
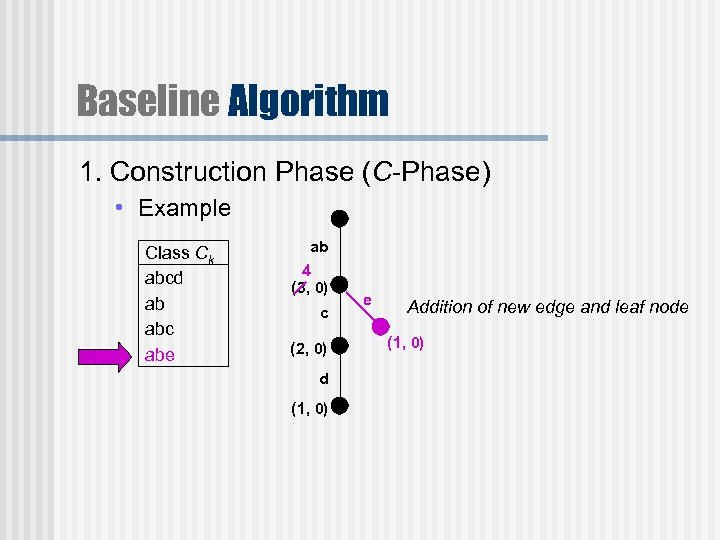
Baseline Algorithm 1. Construction Phase (C-Phase) • Example Class Ck abcd ab abc abe ab 4 (3, 0) c (2, 0) d (1, 0) e Addition of new edge and leaf node (1, 0)

Baseline Algorithm 2. Update Phase (U-Phase) • MT is updated with all the sequences of the opponent class Ck’ Only update c 2 counter for substrings that are already present in the tree, but not introduce any substring that is only present in Dk’ Ø Only internal nodes will be added (no new leaf nodes) Ø • Resultant tree: MT’

Baseline Algorithm 3. e. Xtraction Phase (X-Phase) • All ESs of Ck are extracted by a pre-order tree traversal on MT’ At each node X, we check the values of its counters, s and g, to determine whether its related substrings can satisfy both the support and growth rate conditions Ø If the related substrings of a node X cannot fulfill the support condition, we can ignore the subtree rooted at X Ø § Baseline algorithm: C-U-X phases

s -Pruning Algorithm § Observations • The c 2 counter of each substring in MT would be updated in the U-Phase if it is contained in some sequence in Dk’ • If is infrequent with respect to Dk, it is not qualified to be an ES of Ck and all its descendent nodes will not even be visited in the X-Phase § Pruning idea • To prune infrequent substrings in MT after the CPhase

s -Pruning Algorithm § s-Pruning Phase (Ps-Phase) • With the use of s, all substrings being infrequent in Dk are pruned by a pre-order traversal on MT • Resultant tree: MTs (input to the U-Phase) § s-pruning algorithm: C-Ps-U-X phases

g -Pruning Algorithm § Observations • As sequences in Dk’ are being added to MT, value of the c 2 counter of some nodes would become larger • Support of these nodes' related substrings in Dk’ is monotonically increasing • Ratio of the support of these substrings in Dk to that in Dk’ is monotonically decreasing • At some point, this ratio may become less than g. When this happens, these substrings have actually lost their candidature for being ESs of Ck

g -Pruning Algorithm § Pruning idea • To prune substrings in MT as soon as they are found to be failing the growth rate requirement § g-Update Phase (Ug-Phase) • When the support count of a substring in Dk’ increases, check if it still satisfies the growth rate condition. If not, prune substring by path compression or node deletion • Supported by [istart, iq, iend) representation of edges § g-pruning algorithm: C-Ug-X phases

l-Pruning Algorithm § Observations • Longer substrings often have lower support than shorter ones less likely to fulfill the support condition for ESs • It is not desirable to append these longer substrings to the tree in the C-Phase and subsequently prune them in the Ps-Phase (for the s-pruning algorithm) § Pruning idea • To limit the length of substrings to be added to MT in the tree construction phase

l-Pruning Algorithm § l-Construction Phase (Cl-Phase) • Only match (min(|sj|, l) symbols of each suffix against the tree (ignore the remainder) a smaller MT is built • Unlike the previous two pruning approaches, it may result in ES loss § l-pruning algorithm: Cl-U-X phases

Summary of Phases § Baseline: C-U-X s-pruning: C-Ps-U-X (earlier use of s) g-pruning: C-Ug-X (earlier use of g) l-pruning: Cl-U-X (addition of l) § Combination of the use of pruning techniques • <s , g>, <l , s>, <l , g>, <l , s , g>
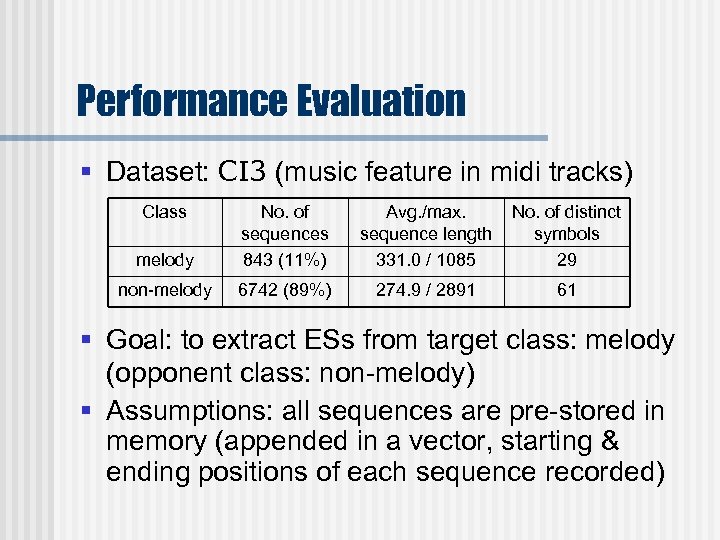
Performance Evaluation § Dataset: CI 3 (music feature in midi tracks) Class melody No. of sequences 843 (11%) Avg. /max. sequence length 331. 0 / 1085 No. of distinct symbols 29 non-melody 6742 (89%) 274. 9 / 2891 61 § Goal: to extract ESs from target class: melody (opponent class: non-melody) § Assumptions: all sequences are pre-stored in memory (appended in a vector, starting & ending positions of each sequence recorded)
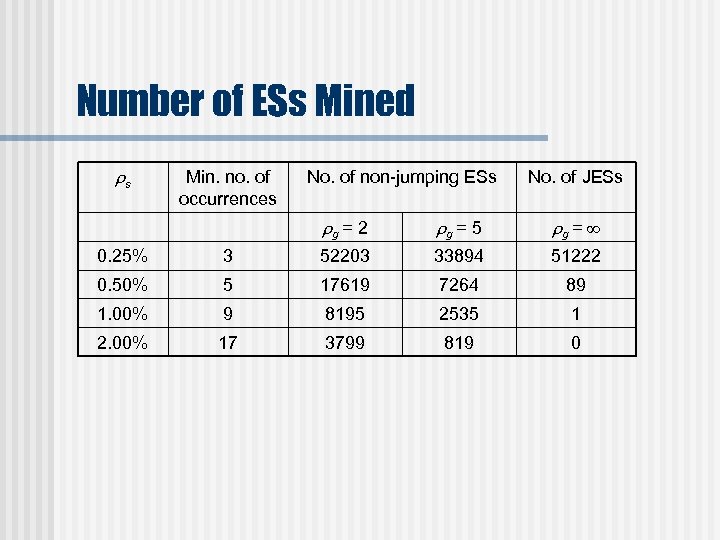
Number of ESs Mined s Min. no. of occurrences No. of non-jumping ESs No. of JESs g = 2 g = 5 g = 0. 25% 3 52203 33894 51222 0. 50% 5 17619 7264 89 1. 00% 9 8195 2535 1 2. 00% 17 3799 819 0
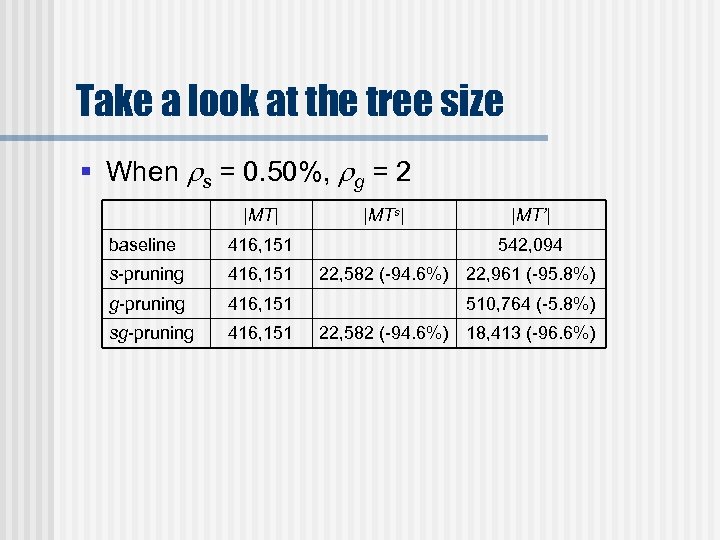
Take a look at the tree size § When s = 0. 50%, g = 2 |MT| |MTs| |MT’| baseline 416, 151 542, 094 s-pruning 416, 151 22, 582 (-94. 6%) 22, 961 (-95. 8%) g-pruning 416, 151 510, 764 (-5. 8%) sg-pruning 416, 151 22, 582 (-94. 6%) 18, 413 (-96. 6%)
![Baseline Algorithm [C-U-X ] § Performance: same for all s and g § Time: Baseline Algorithm [C-U-X ] § Performance: same for all s and g § Time:](https://present5.com/presentation/45a6ab039df4860df405d9c83594f81e/image-35.jpg)
Baseline Algorithm [C-U-X ] § Performance: same for all s and g § Time: about 35 s
![s -Pruning Algorithm [C-Ps-U-X ] § Faster than baseline alg. by 25 -45% § s -Pruning Algorithm [C-Ps-U-X ] § Faster than baseline alg. by 25 -45% §](https://present5.com/presentation/45a6ab039df4860df405d9c83594f81e/image-36.jpg)
s -Pruning Algorithm [C-Ps-U-X ] § Faster than baseline alg. by 25 -45% § But reduction in time < reduction in tree size § Performance: improve with in s, same for all g
![g -Pruning Algorithm [C-Ug-X ] § When g = , faster than baseline alg. g -Pruning Algorithm [C-Ug-X ] § When g = , faster than baseline alg.](https://present5.com/presentation/45a6ab039df4860df405d9c83594f81e/image-37.jpg)
g -Pruning Algorithm [C-Ug-X ] § When g = , faster than baseline alg. by 2 -5% § When g = 2 or 5, slower than baseline alg. by 1 -4% § Performance: improve with in g, same for all s
![sg -Pruning Algorithm [C-Ps-Ug-X ] § Faster than baseline, s-pruning, g-pruning alg. (all cases) sg -Pruning Algorithm [C-Ps-Ug-X ] § Faster than baseline, s-pruning, g-pruning alg. (all cases)](https://present5.com/presentation/45a6ab039df4860df405d9c83594f81e/image-38.jpg)
sg -Pruning Algorithm [C-Ps-Ug-X ] § Faster than baseline, s-pruning, g-pruning alg. (all cases) § Faster than baseline alg. for 31 -54%(2 or 5), 47 -81%( ) § Performance: improve with in s and g
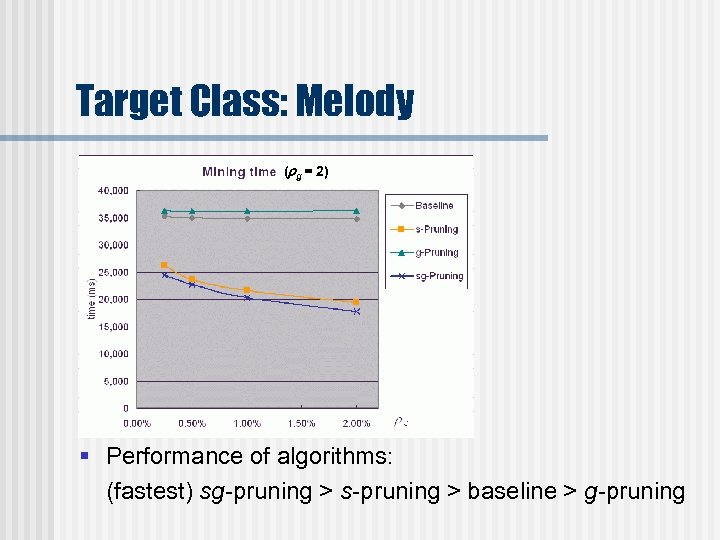
Target Class: Melody ( g = 2) § Performance of algorithms: (fastest) sg-pruning > s-pruning > baseline > g-pruning
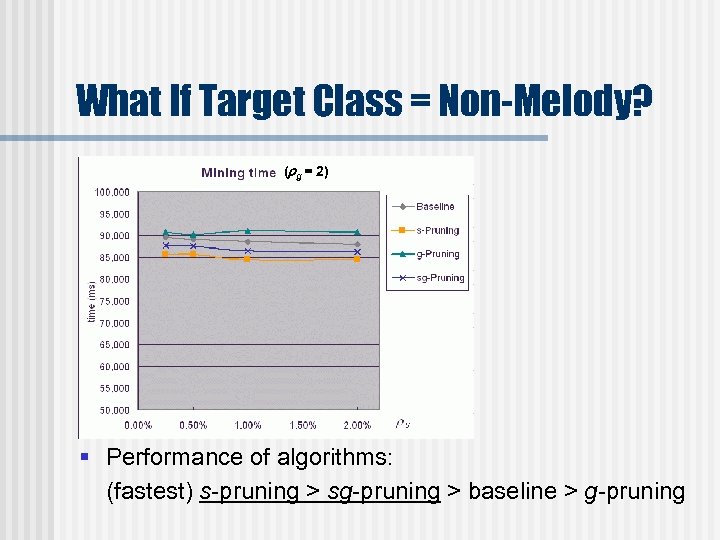
What If Target Class = Non-Melody? ( g = 2) § Performance of algorithms: (fastest) s-pruning > sg-pruning > baseline > g-pruning

What If Target Class = Non-Melody? § sg-pruning performs worse than s-pruning • Due to overhead in node creation (g-pruning requires one more index for each edge) § Not much performance gain with s-pruning (just 3 -5%) or sg-pruning (1 -3%) • Bottleneck: formation of MT (over 93% time is spent in the C-Phase) • In fact, these pruning techniques are very effective since much time is saved in the U-Phase Ø 42 -80% (for s-pruning) and 54 -85% (for sg-pruning)
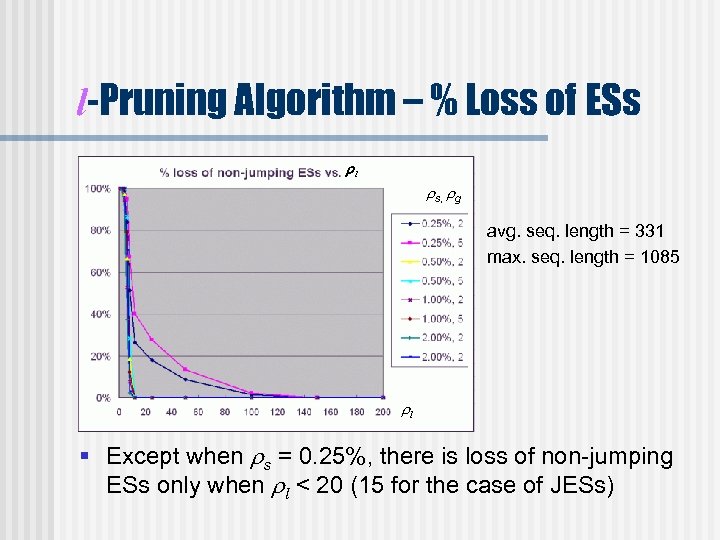
l-Pruning Algorithm – % Loss of ESs l s, g avg. seq. length = 331 max. seq. length = 1085 l § Except when s = 0. 25%, there is loss of non-jumping ESs only when l < 20 (15 for the case of JESs)
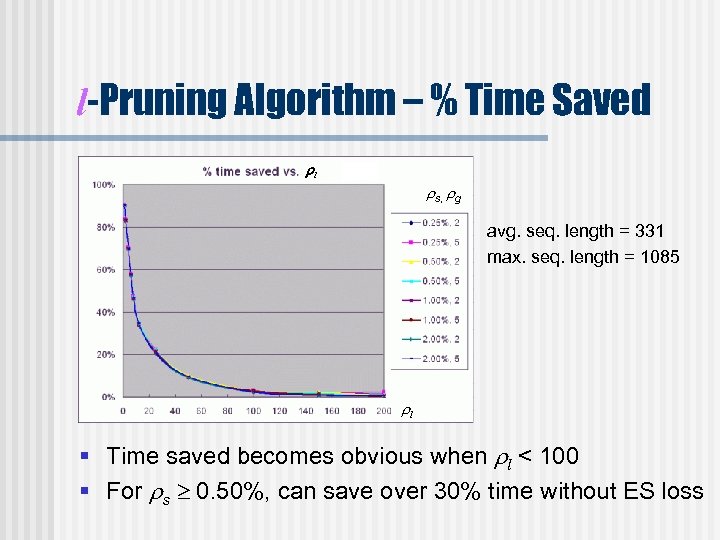
l-Pruning Algorithm – % Time Saved l s, g avg. seq. length = 331 max. seq. length = 1085 l § Time saved becomes obvious when l < 100 § For s 0. 50%, can save over 30% time without ES loss

To be Explored. . . § ls-pruning § lg-pruning § lsg-pruning

Conclusions § ESs of a class are substrings which occur more frequently in that class rather than other classes. § ESs are useful features as they capture distinguishing characteristics of data classes. § We have proposed a suffix tree-based framework for mining ESs.

Conclusions § Three basic techniques for pruning ES candidates have been described, and most of them have been proven effective § Future work: to study whether pruning techniques can be efficiently applied to suffix tree merging algorithms or other ES mining models.

Applying Pruning Techniques to Single. Class Emerging Substring Mining - The End -
45a6ab039df4860df405d9c83594f81e.ppt