Applications of Game Theory Part II b John C

Applications of Game Theory Part II(b) John C. S. Lui Computer Science & Eng. Dept The Chinese University of Hong Kong

First course On the interaction between Overlay Routing and Underlay Routing Y. Liu, H. Zhang, W. Gong, D. Towsley INFOCOM 2005

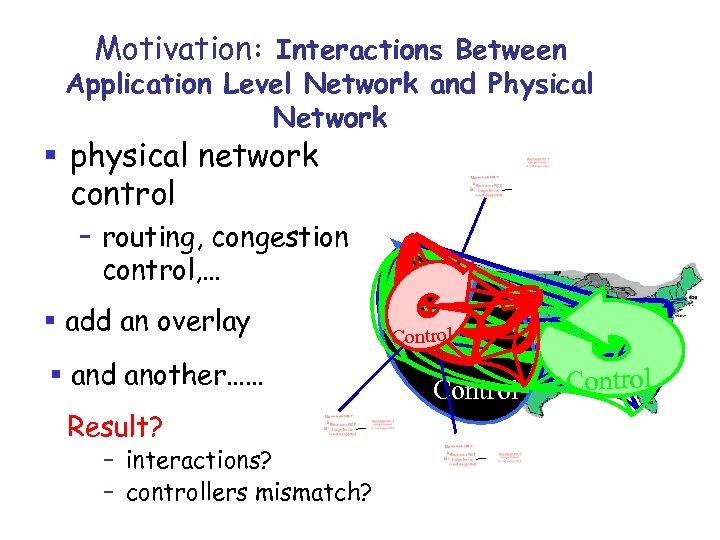
Motivation: Interactions Between Application Level Network and Physical Network § physical network control – routing, congestion control, … § add an overlay § and another…… Result? – interactions? – controllers mismatch? Control

Outline § § Problem Formulation Simulation Study Game-theoretic Study Conclusions

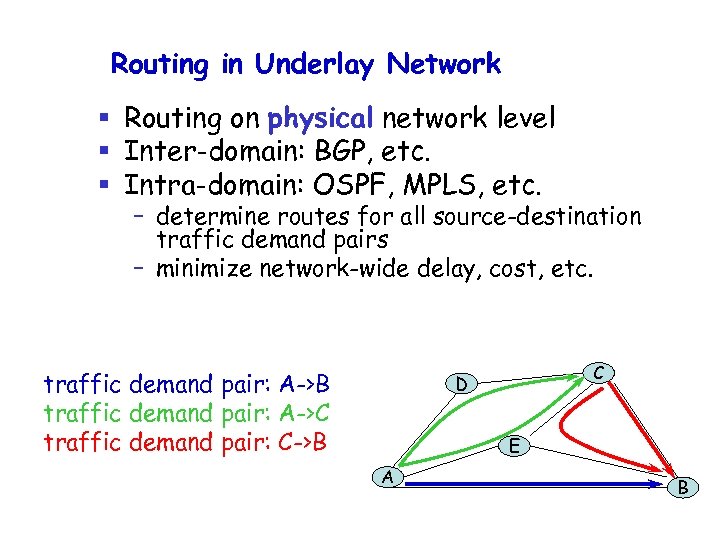
Routing in Underlay Network § Routing on physical network level § Inter-domain: BGP, etc. § Intra-domain: OSPF, MPLS, etc. – determine routes for all source-destination traffic demand pairs – minimize network-wide delay, cost, etc. traffic demand pair: A->B traffic demand pair: A->C traffic demand pair: C->B C D E A B

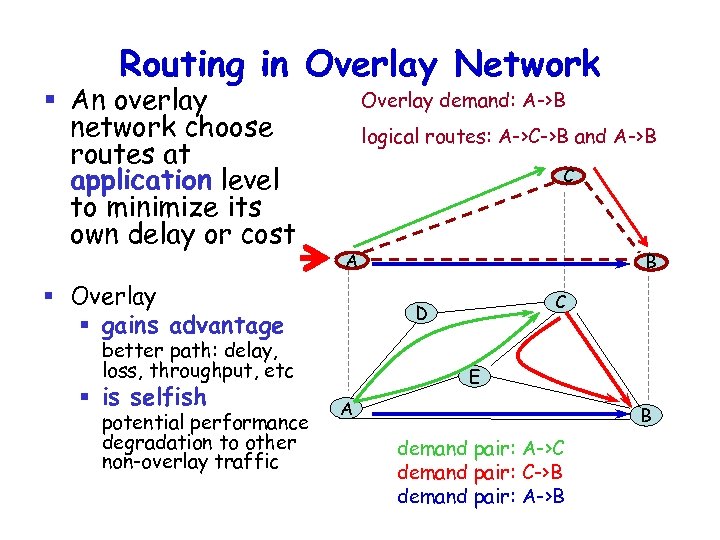
Routing in Overlay Network § An overlay network choose routes at application level to minimize its own delay or cost Overlay demand: A->B logical routes: A->C->B and A->B C A § Overlay § gains advantage potential performance degradation to other non-overlay traffic C D better path: delay, loss, throughput, etc § is selfish B E A B demand pair: A->C demand pair: C->B demand pair: A->B

Considering overlay and underlay together ? § How do they interact with each other? § How does selfish behavior of overlay routing – affect overall network performance? – affect non-overlay traffic performance? – affect its own performance?

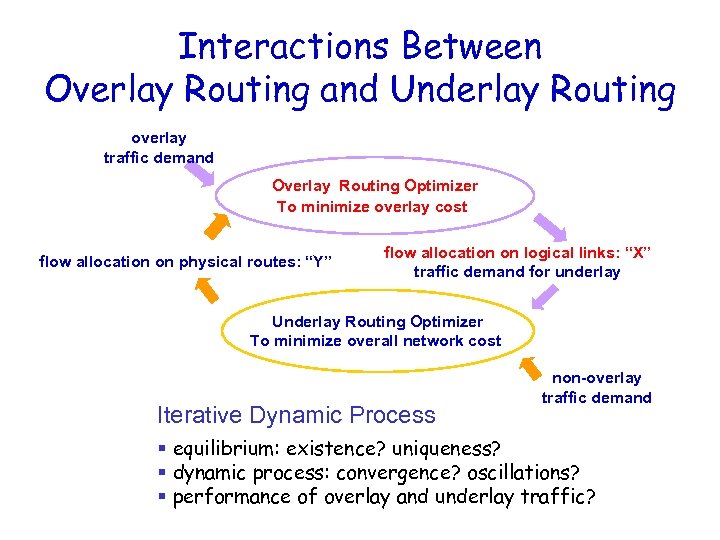
Interactions Between Overlay Routing and Underlay Routing overlay traffic demand Overlay Routing Optimizer To minimize overlay cost flow allocation on physical routes: “Y” flow allocation on logical links: “X” traffic demand for underlay Underlay Routing Optimizer To minimize overall network cost Iterative Dynamic Process non-overlay traffic demand § equilibrium: existence? uniqueness? § dynamic process: convergence? oscillations? § performance of overlay and underlay traffic?

Approach by authors § Focusing interaction in a single AS § Considering two routing models for overlay and one routing model for underlay § Simulating the interaction dynamic process § Studying this process in a Game-theoretic framework

Routing Models § Overlay routing model – Selfish source routing § Individual user controls infinitesimal amount of traffic, to minimize its own delay – Optimal overlay routing § A central entity minimizes the total delay of all overlay traffic demands § Underlay routing model § Optimal underlay routing § A central entity minimizes the total delay of all network traffic, e. g. Traffic Engineering MPLS

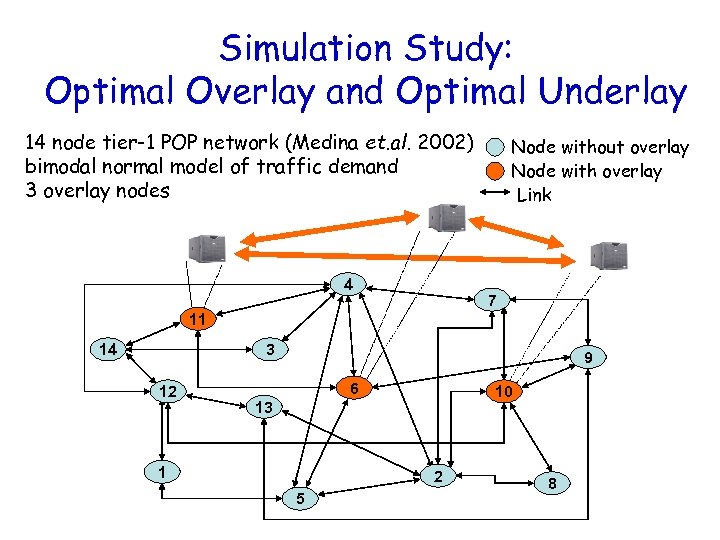
Simulation Study: Optimal Overlay and Optimal Underlay 14 node tier-1 POP network (Medina et. al. 2002) bimodal normal model of traffic demand 3 overlay nodes 4 Node without overlay Node with overlay Link 7 11 14 3 12 9 6 10 13 1 2 5 8

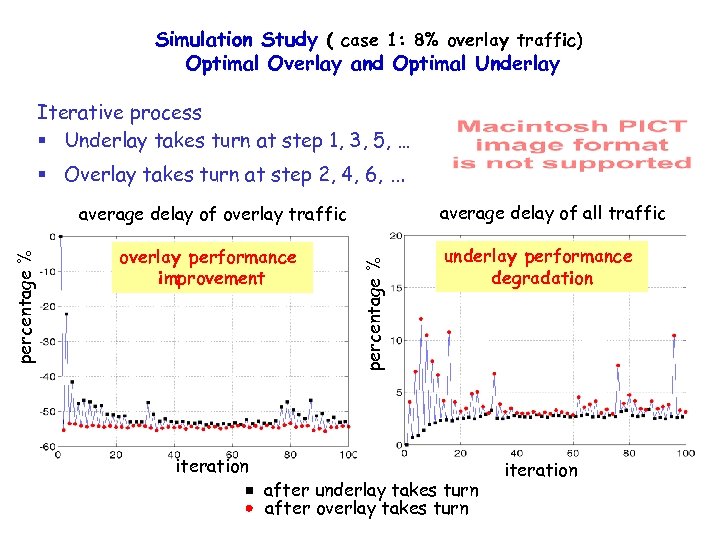
Simulation Study ( case 1: 8% overlay traffic) Optimal Overlay and Optimal Underlay Iterative process § Underlay takes turn at step 1, 3, 5, … § Overlay takes turn at step 2, 4, 6, … average delay of all traffic overlay performance improvement iteration percentage % average delay of overlay traffic underlay performance degradation after underlay takes turn after overlay takes turn iteration

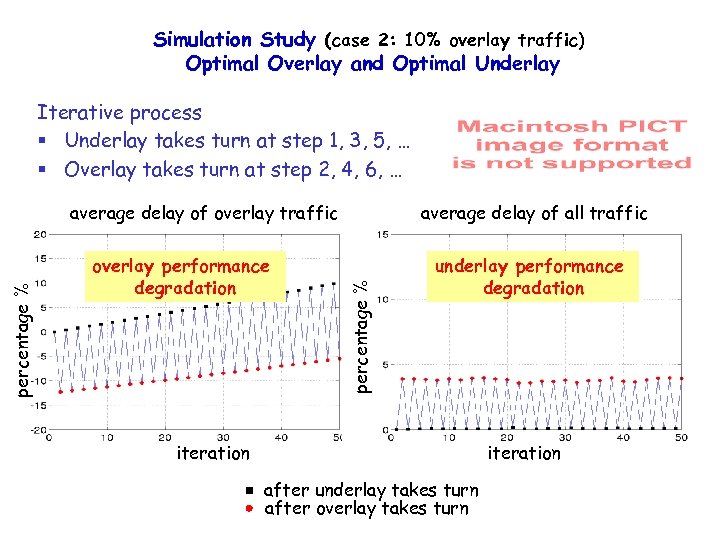
Simulation Study (case 2: 10% overlay traffic) Optimal Overlay and Optimal Underlay Iterative process § Underlay takes turn at step 1, 3, 5, … § Overlay takes turn at step 2, 4, 6, … overlay performance degradation average delay of all traffic percentage % average delay of overlay traffic underlay performance degradation iteration after underlay takes turn after overlay takes turn

Game-theoretic Study § Two-player non-zero sum game Underlay overlay X: strategy of “overlay” traffic allocation on logical links Y: strategy of “underlay” traffic allocation on physical links : Cost of “overlay” : Cost of “underlay” : Constraints of “overlay” : Constraints of “underlay”

Game-theoretic Study • Best-reply dynamics • Nash Equilibrium

Optimal Underlay Routing v. s. Optimal Overlay Routing § Overlay – One central entity calculates routes for all overlay demands, given current underlay routing – Assumption: it knows underlay topology and background traffic C X(k) A 1 -X(k) B Denote overlay’s routing decision with a single variable X(k): overlay’s flow on path ACB after round k

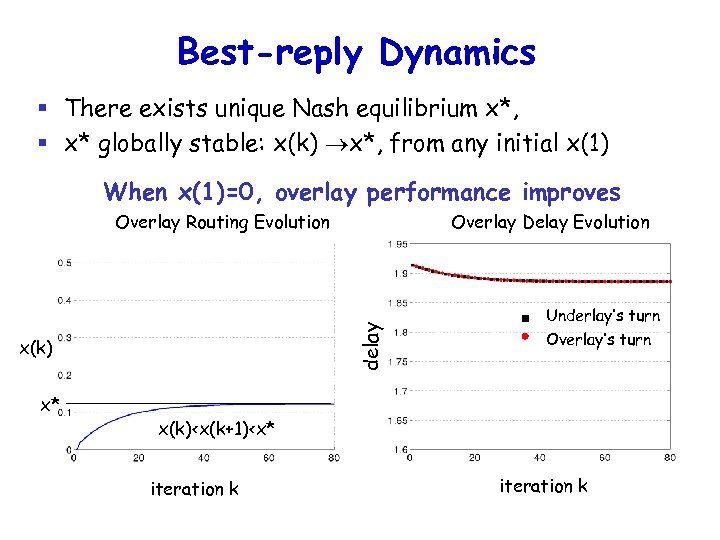
Best-reply Dynamics § There exists unique Nash equilibrium x*, § x* globally stable: x(k) x*, from any initial x(1) When x(1)=0, overlay performance improves x(k) x* Overlay Delay Evolution delay Overlay Routing Evolution Underlay’s turn Overlay’s turn x(k)<x(k+1)<x* iteration k

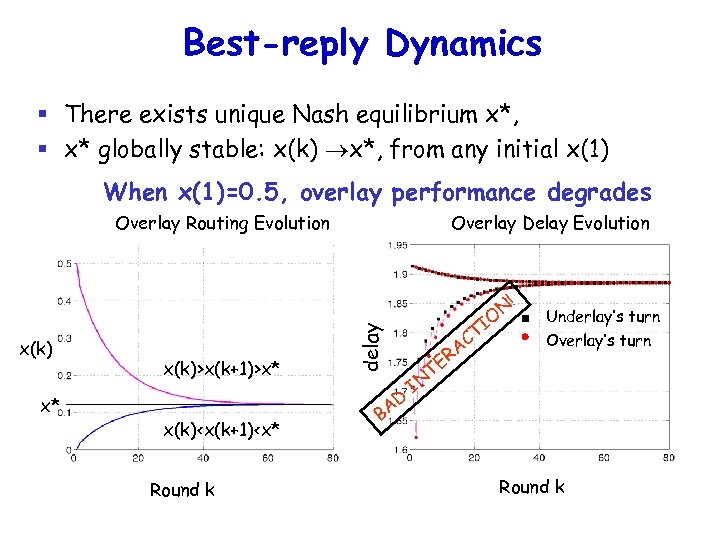
Best-reply Dynamics § There exists unique Nash equilibrium x*, § x* globally stable: x(k) x*, from any initial x(1) When x(1)=0. 5, overlay performance degrades Overlay Routing Evolution Overlay Delay Evolution ! x(k) x* x(k)>x(k+1)>x* x(k)<x(k+1)<x* Round k delay N AD B O TI TE IN AC R Underlay’s turn Overlay’s turn Round k

Conclusions & Open Issues § Selfish overlay routing can degrade performance of network as a whole § Interactions between blind optimizations at two levels may lead to lose-lose situation § Future work: – – – larger topology: analysis/experimentation overlay routing and inter-domain routing interactions between multiple overlays (****) implications on design overlay routing regulation between overlay and underlay (****)

Second course On the Interaction of Multiple Overlay Routings Performance 2005 Joe W. J. Jiang, D. M. Chiu, John C. S. Lui

Questions • These overlays tend to fully utilize available resource. • So, is there any anarchy? • How do overlay networks co-exist with each other? • What is the implication of interactions? • How to regulate selfish overlay networks via mechanism design? • Can ISPs take advantage of this?

Outline • • • Motivation Mathematical Modeling Overlay Routing Game Implications of Interaction Pricing Conclusion

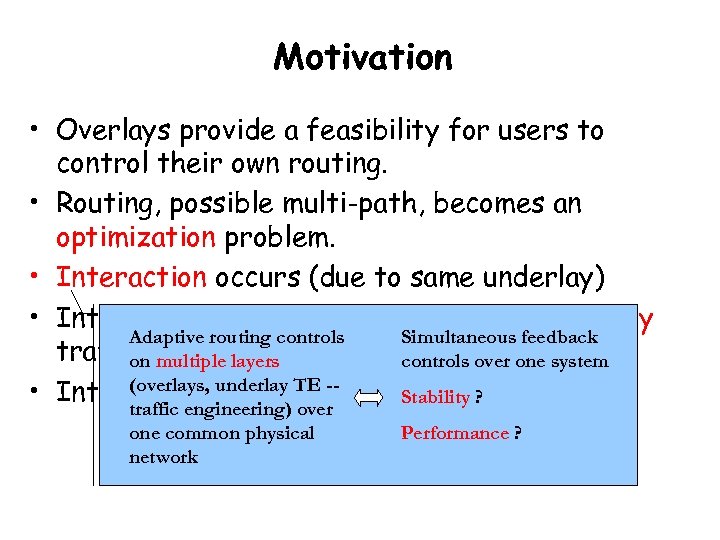
Motivation • Overlays provide a feasibility for users to control their own routing. • Routing, possible multi-path, becomes an optimization problem. • Interaction occurs (due to same underlay) • Interaction between one overlay and underlay Adaptive routing controls Simultaneous feedback traffic multiple layers Zhang controls over one system et al, Infocom’ 05. on engineering, (overlays, between co-existing overlays ? • Interaction underlay TE -Stability ? traffic engineering) over one common physical network Performance ?

Performance Characteristics • Objective: minimize end-to-end delay (e. g. , RON) • Delay of a physical link e: de(le) l – aggregate traffic traversing link e e • Performance Characteristics (Underlay) Average delay ( f : flow)

Performance Characteristics • Objective: minimize end-to-end delay • Delay of a physical link e: de(le) le – aggregate traffic traversing link e • Performance Characteristics (Underlay) Average delay (multipath routing)

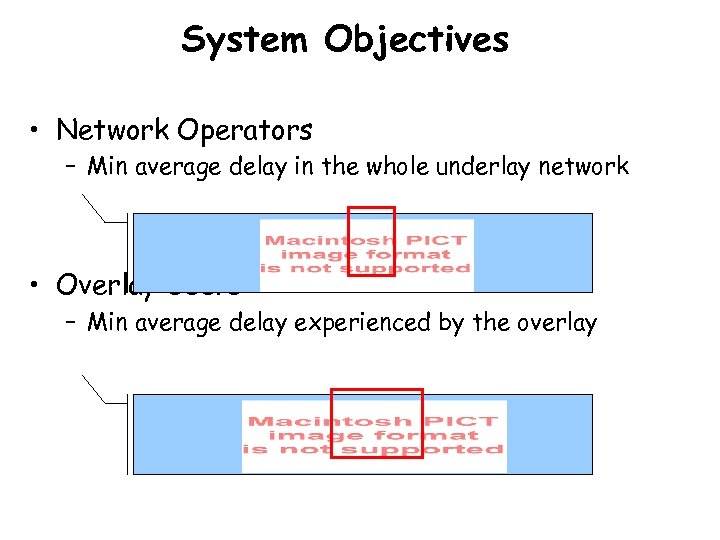
System Objectives • Network Operators – Min average delay in the whole underlay network • Overlay Users – Min average delay experienced by the overlay

How do Overlays Interact? • • • Overlapping physical links. Performance dependent on each other. Selfish routing optimization. Overlays are transparent to each other. Lack of information exchange between overlays.

Contribution • What is the form of interaction? • Is there routing instability (oscillation), or there is an equilibrium ? • Is the routing equilibrium efficient? • What is the price of anarchy? • Fairness issues • Mechanism design: can we lead the selfish behaviors to an efficient equilibrium?

Mathematical Modeling • Overlay routing: An optimization problem n Decision variable: routing policy s: overlay f: flow r: path

Mathematical Modeling • Overlay routing: An optimization problem Objective: average weighted delay (matrix form ) n Routing Matrix Delay Function (vector form)

Overlay Routing Optimization n Convex programming Capacity Constraint n n n Non-negative Flow Constraint Demand constraint (fixed transmission demand)

Algorithmic Solution • Unique optimizer – Convex programming – feasible region: convex – delay function: continuous, non-decreasing, strictly convex • Solution – Apply any convex programming techniques. – Marginal cost network flow (probabilistic routing ICNP’ 04). – This is solved in an independent, and distributed fashion by each overlay. But will independent optimization leads to system instability (route flop)?

Overlay Routing Game Strategic Game: Goverlay<N, ( s), (≥s)> • Nash Routing Game – Player -- N all overlays – Strategy -- s feasible routing policy: feasible region of OVERLAY(s) – Preference relation -- ≥s low delay: player’s utility function is -delay(s)

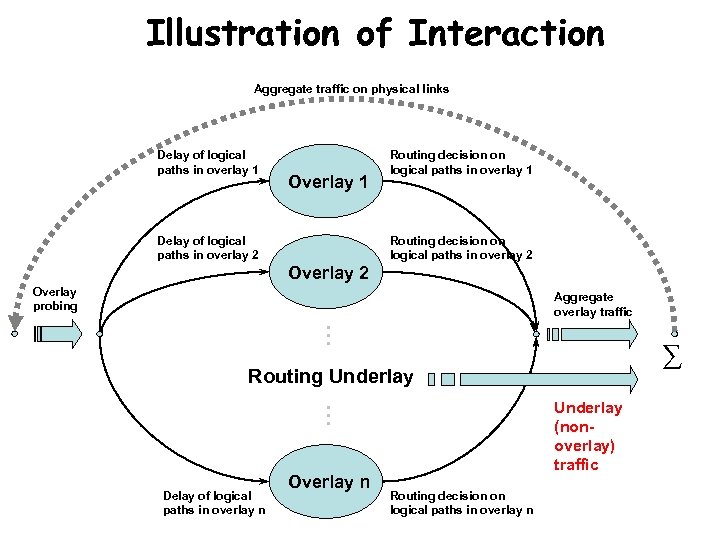
Illustration of Interaction Aggregate traffic on physical links Delay of logical paths in overlay 1 Overlay 1 Delay of logical paths in overlay 2 Routing decision on logical paths in overlay 1 Routing decision on logical paths in overlay 2 Overlay probing Aggregate overlay traffic … ∑ Routing Underlay … Underlay (nonoverlay) traffic Delay of logical paths in overlay n Overlay n Routing decision on logical paths in overlay n

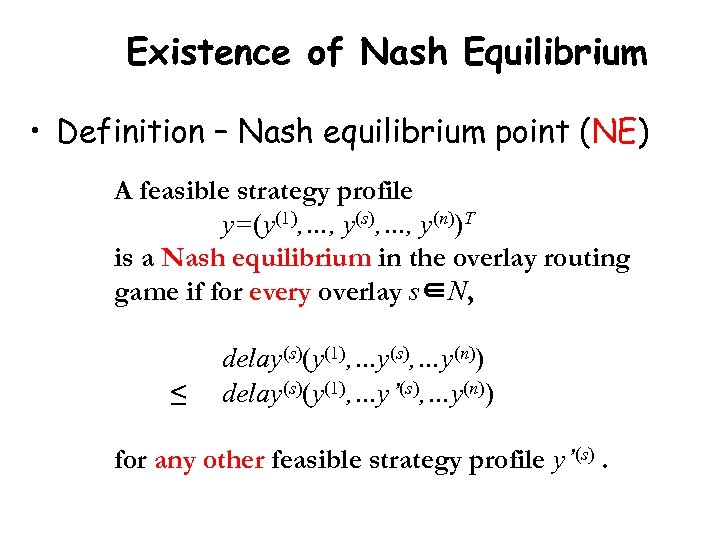
Existence of Nash Equilibrium • Definition – Nash equilibrium point (NE) A feasible strategy profile y=(y(1), …, y(s), …, y(n))T is a Nash equilibrium in the overlay routing game if for every overlay s∈N, ≤ delay(s)(y(1), …y(s), …y(n)) delay(s)(y(1), …y’(s), …y(n)) for any other feasible strategy profile y’(s).

Existence of Nash Equilibrium • Theorem Good News: NO ROUTE FLOP !!! In the overlay routing game, there exists a Nash equilibrium if the delay function delay(s)(y(s) ; y(-s)) is continuous, non-decreasing and convex.

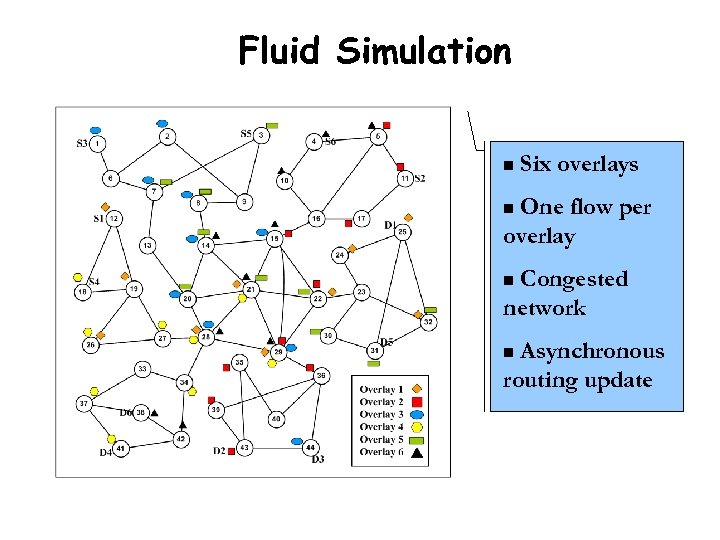
Fluid Simulation n Six overlays One flow per overlay n Congested network n Asynchronous routing update n

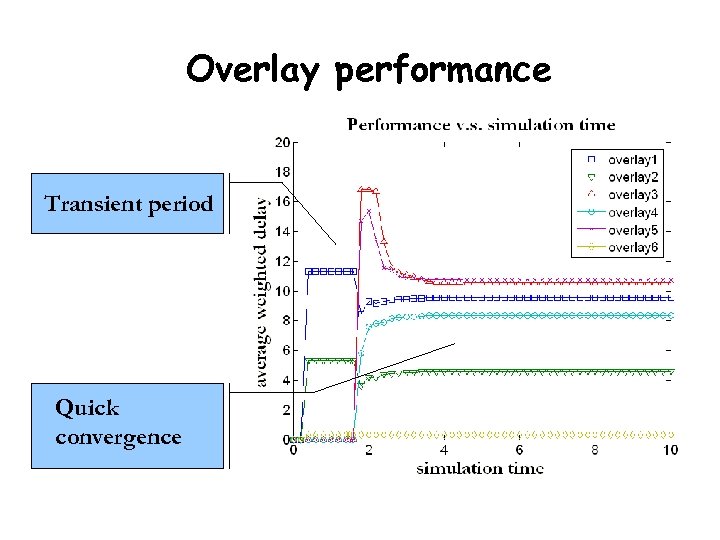
Overlay performance Transient period Quick convergence

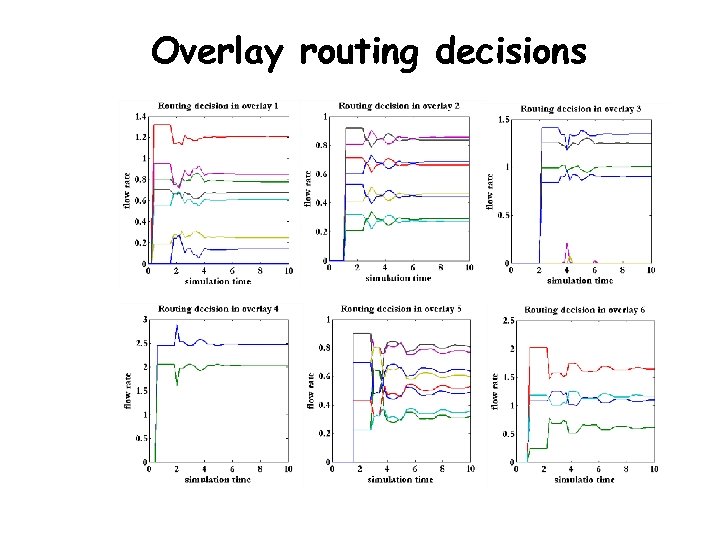
Overlay routing decisions

The Price of Anarchy Global Performance (average delay for all flows) GOR NSR Efficiency Loss ? • GOR: Global Optimal Routing • NOR: Nash equilibrium for Overlay Routing Game • NSR: Nash equilibrium for Selfish Routing

Selfish Routing • (User) selfish routing: a single packet’s selfishness • Every single packet chooses to route via a shortest (delay) path. • A flow is at Nash equilibrium if no packet can improve its delay by changing its route.

Selfish Routing • Also a Nash equilibrium of a mixed strategic game – Player: flow { f } – Strategy: p Pf – Preference: low delay • System Optimization Problem

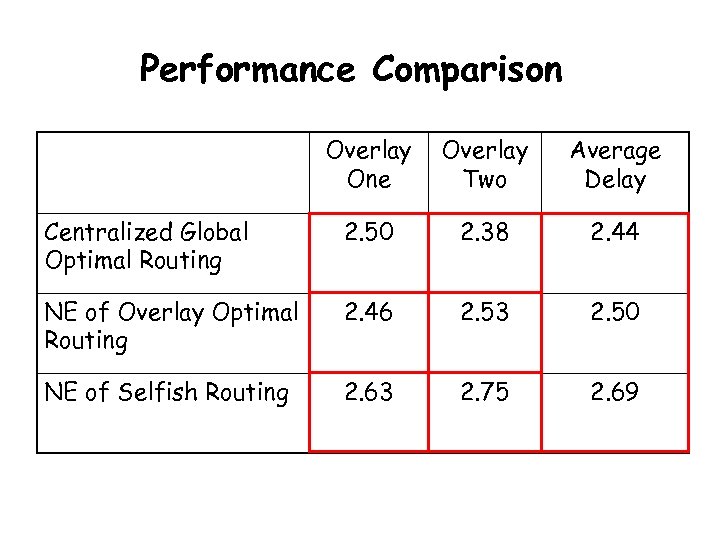
Performance Comparison Overlay One Overlay Two Average Delay Centralized Global Optimal Routing 2. 50 2. 38 2. 44 NE of Overlay Optimal Routing 2. 46 2. 53 2. 50 NE of Selfish Routing 2. 63 2. 75 2. 69

Inspiration • Is the equilibrium point efficient (at least Pareto optimal) ? • Fairness issues of resource competition between overlays.

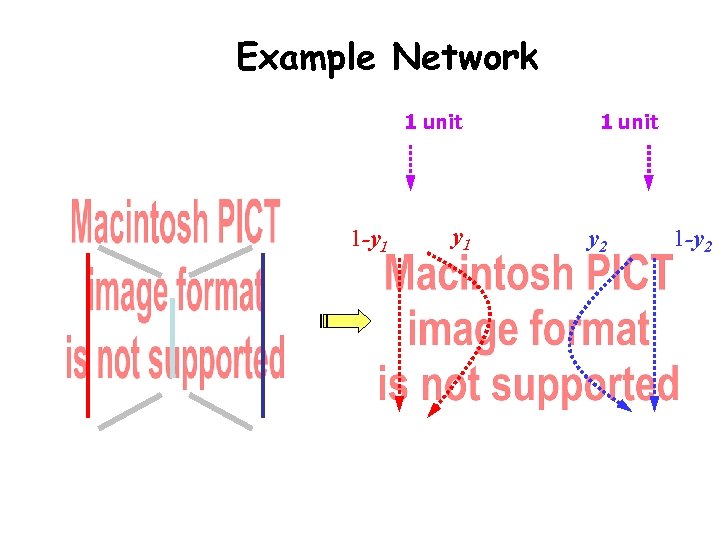
Example Network 1 unit 1 -y 1 1 unit y 2 1 -y 2

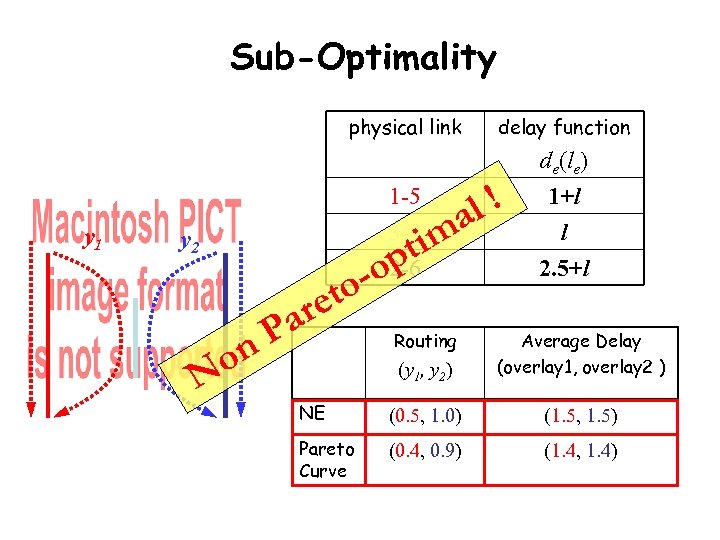
Sub-Optimality physical link y 1 delay function l! a im t 1 -5 3 -4 y 2 p o 2 -6 o- et ar o N P n Routing de(le) 1+l l 2. 5+l (y 1, y 2) Average Delay (overlay 1, overlay 2 ) NE (0. 5, 1. 0) (1. 5, 1. 5) Pareto Curve (0. 4, 0. 9) (1. 4, 1. 4)

Fairness Paradox physical link y 1 1 -5 3 -4 de(le) a+l bl 2 -6 y 2 delay function c+l a, b, c, are non-negative parameters p Everything is symmetric except two private links – a & c p

Fairness Paradox physical link y 1 y 2 delay function 1 -5 3 -4 de(le) a+l bl 2 -6 c+l a<c Overlay 1 has a better “private” link !

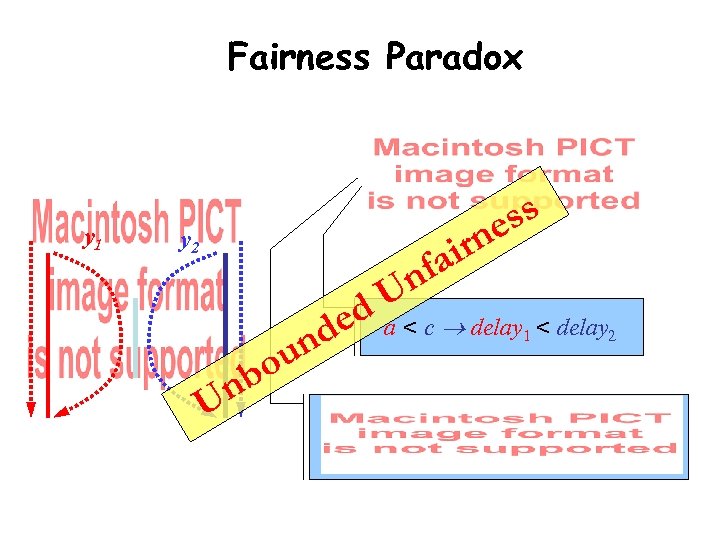
Fairness Paradox y 1 y 2 fa n U ss ne ir ed a < c delay < delay d n U un bo 1 2

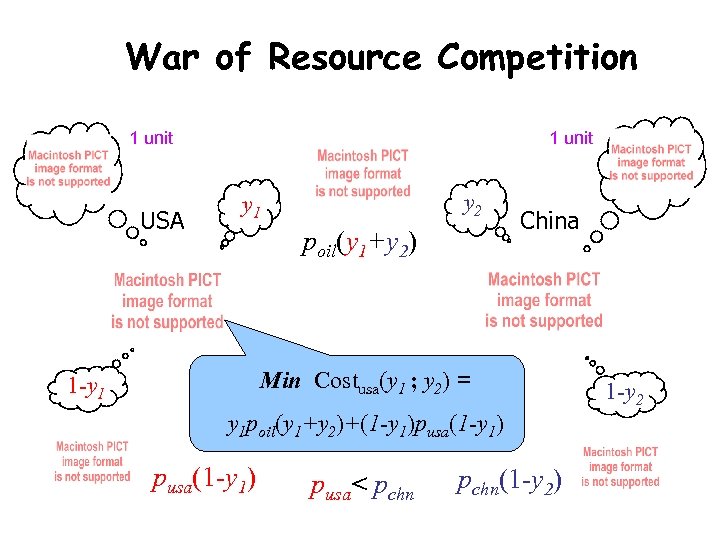
War of Resource Competition 1 unit USA 1 unit y 2 y 1 poil(y 1+y 2) China Min Costusa(y 1 ; y 2) = 1 -y 1 y 1 poil(y 1+y 2)+(1 -y 1)pusa(1 -y 1) pusa< pchn(1 -y 2) 1 -y 2

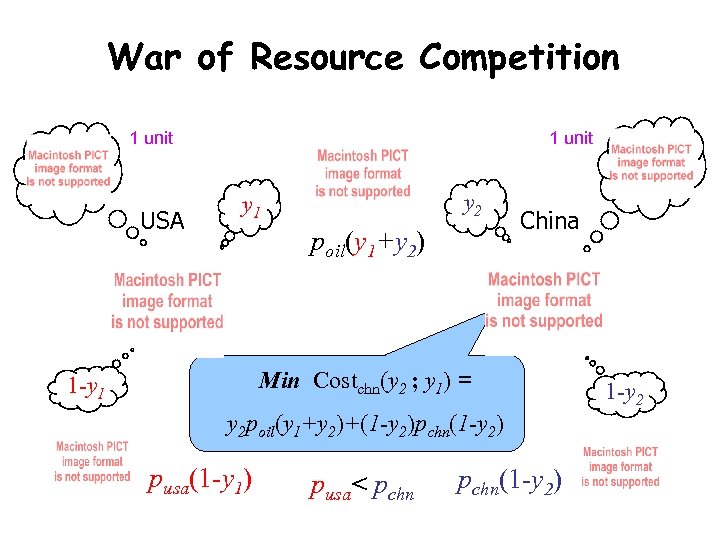
War of Resource Competition 1 unit USA 1 unit y 2 y 1 poil(y 1+y 2) China Min Costchn(y 2 ; y 1) = 1 -y 1 y 2 poil(y 1+y 2)+(1 -y 2)pchn(1 -y 2) pusa(1 -y 1) pusa< pchn(1 -y 2) 1 -y 2

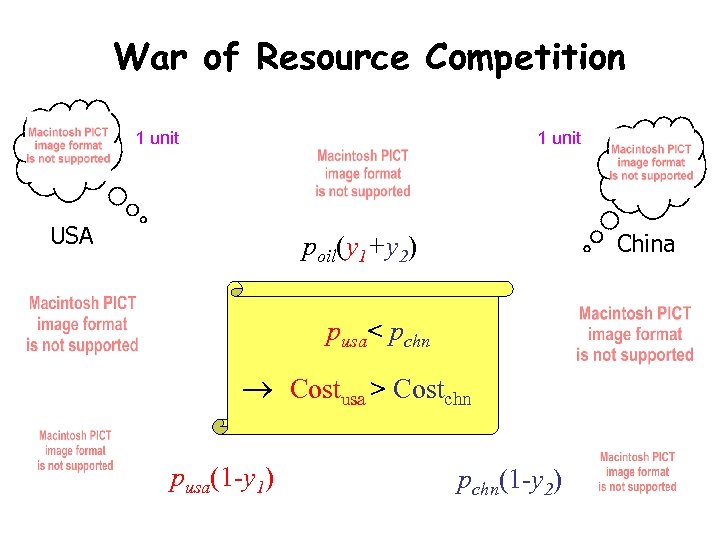
War of Resource Competition 1 unit USA China poil(y 1+y 2) pusa< pchn Costusa > Costchn pusa(1 -y 1) pchn(1 -y 2)

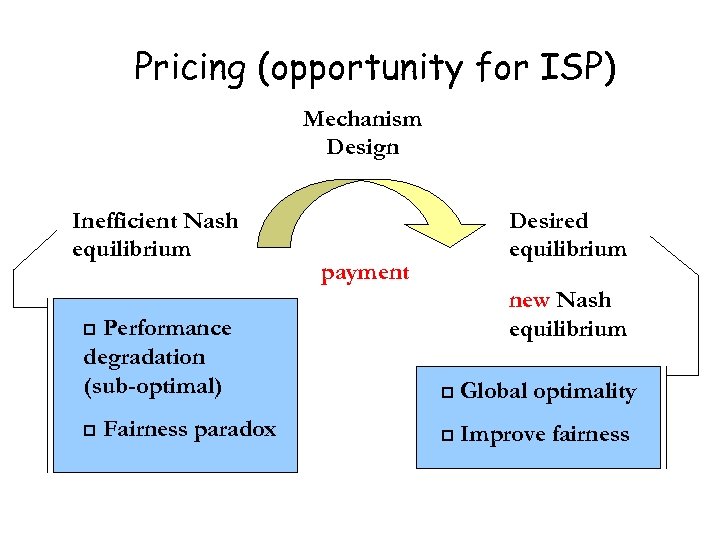
Pricing (opportunity for ISP) Mechanism Design Inefficient Nash equilibrium Performance degradation (sub-optimal) Desired equilibrium payment new Nash equilibrium p p Fairness paradox p Global optimality p Improve fairness

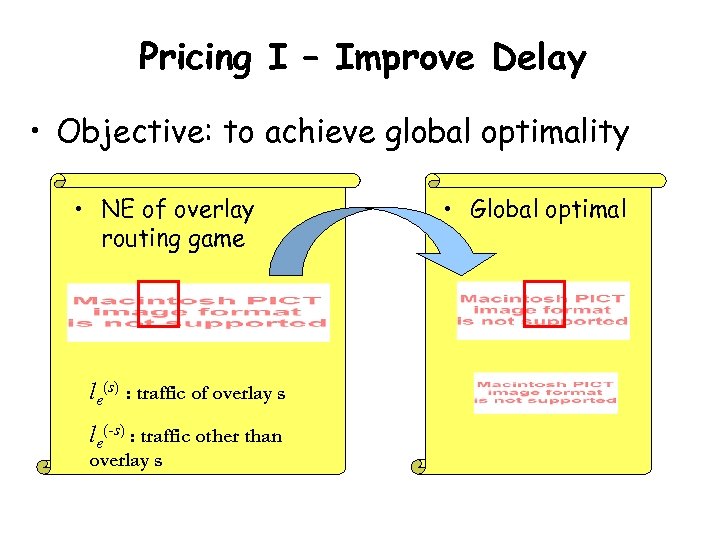
Pricing I – Improve Delay • Objective: to achieve global optimality • NE of overlay routing game le(s) : traffic of overlay s le(-s) : traffic other than overlay s • Global optimal

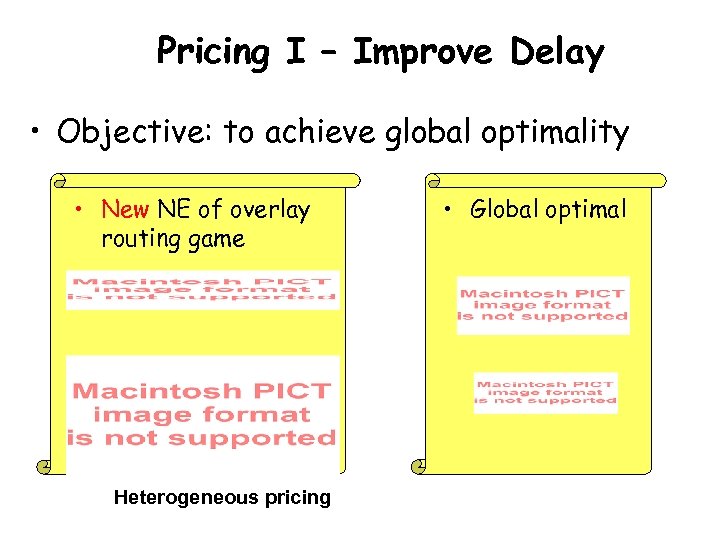
Pricing I – Improve Delay • Objective: to achieve global optimality • New NE of overlay routing game Heterogeneous pricing • Global optimal

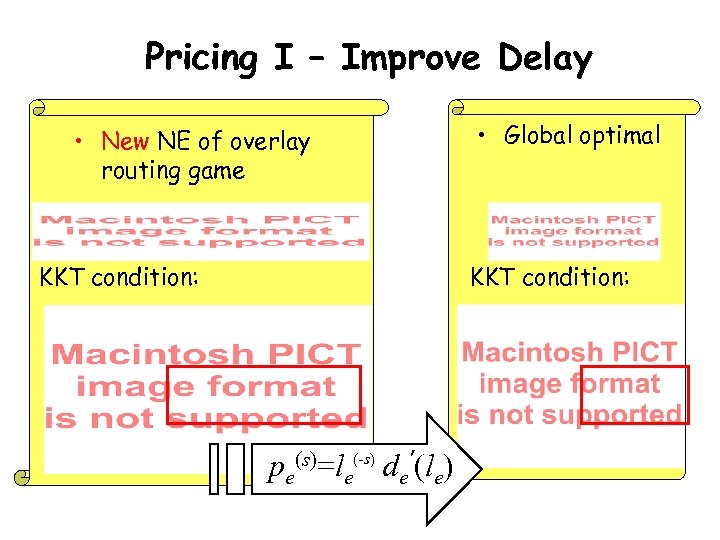
Pricing I – Improve Delay • New NE of overlay routing game KKT condition: • Global optimal KKT condition: pe(s)=le(-s) de’(le)

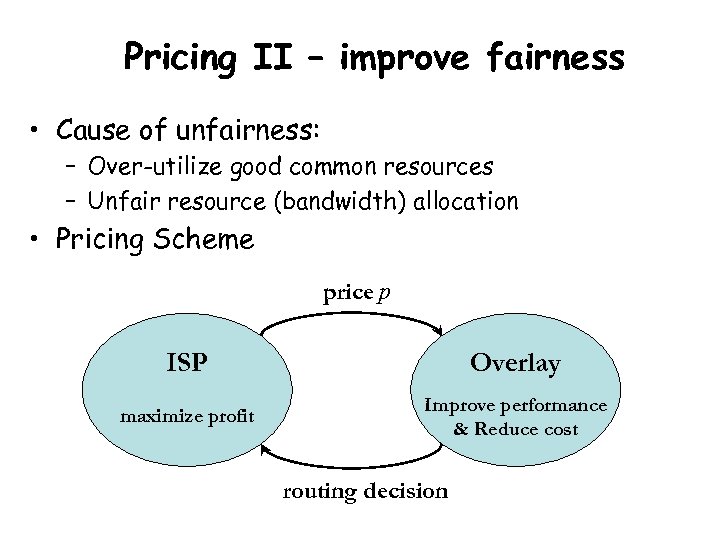
Pricing II – improve fairness • Cause of unfairness: – Over-utilize good common resources – Unfair resource (bandwidth) allocation • Pricing Scheme price p ISP Overlay maximize profit Improve performance & Reduce cost routing decision

Incentive Resource Allocation • For overlays: : sensitivity factor new Nash equilibrium {le}

Revenue Distribution • For ISPs (links): : profit of link e : revenue : operating cost --

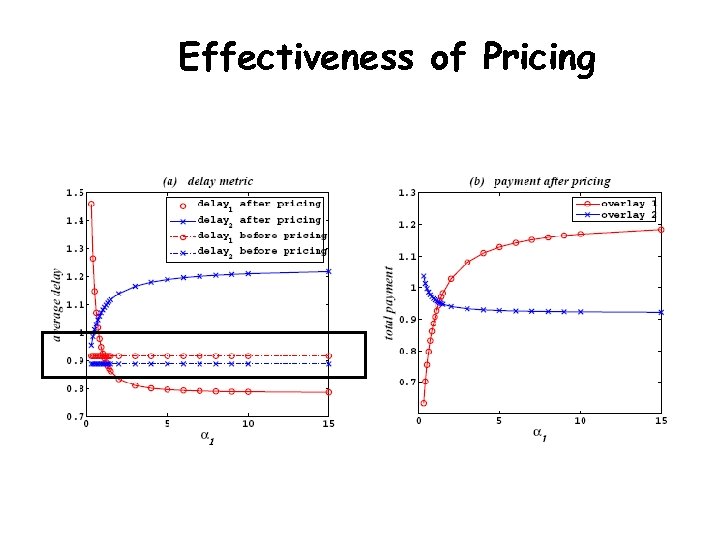
Effectiveness of Pricing

Conclusion • Study the interaction between multiple coexisting overlays. • Non-cooperative Nash routing game. • Prove the existence of NEP. • Show the anomalies and implications of the NEP. • Present two distributed pricing schemes to address the anomalies.

Third Course Interaction of ISPs: Distributed Resource Allocation and Revenue Maximization Sam C. M. Lee, Joe W. J. Jiang, D. M Chiu, John C. S. Lui

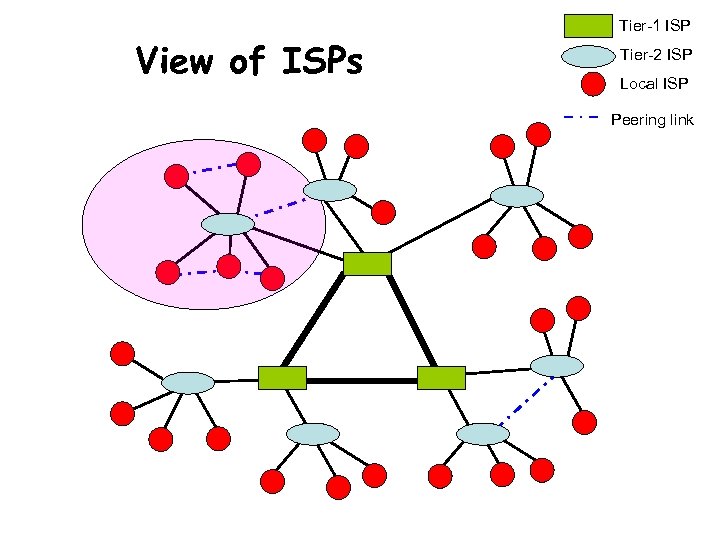
View of ISPs Tier-1 ISP Tier-2 ISP Local ISP Peering link

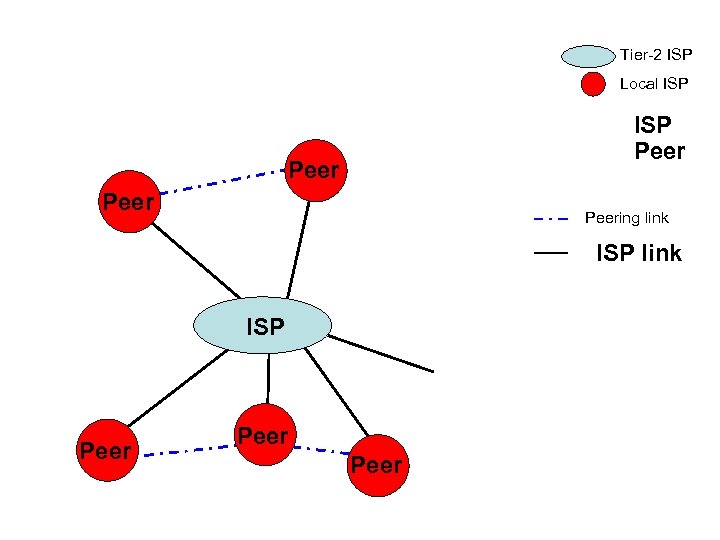
Tier-2 ISP Local ISP Peering link ISP Peer

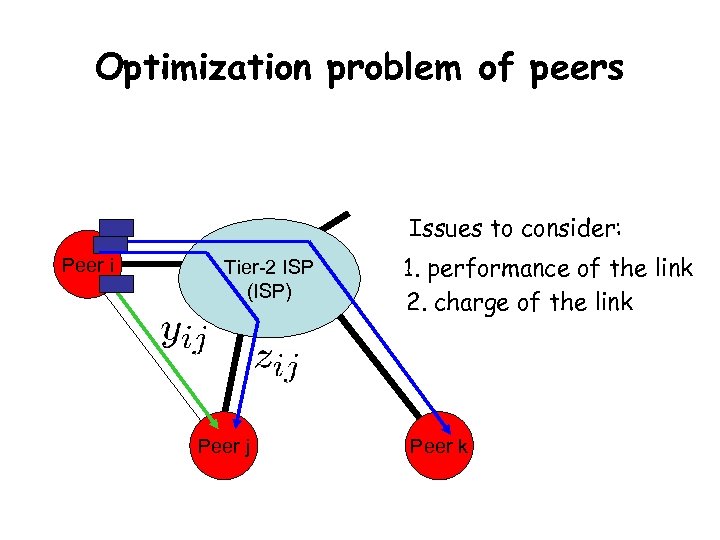
Optimization problem of peers Issues to consider: Peer i Tier-2 ISP (ISP) Peer j 1. performance of the link 2. charge of the link Peer k

Optimization problem of peers Happiness obtained from sending traffic to peers Delay cost in ISP link Payment to ISP Delay costs in peering links Payments to peers

Constraints of peers 1. 2. 3. 4.

Solution to the peers • Objective function is strictly concave in every transmission rate • The optimal transmission rates and maximum utility are unique and can be found by the Lagrangian method.

Problems for an ISP • Resource distribution – How to determine the capacity for the peers • Maximization of revenue – How to determine the optimal value of unit price

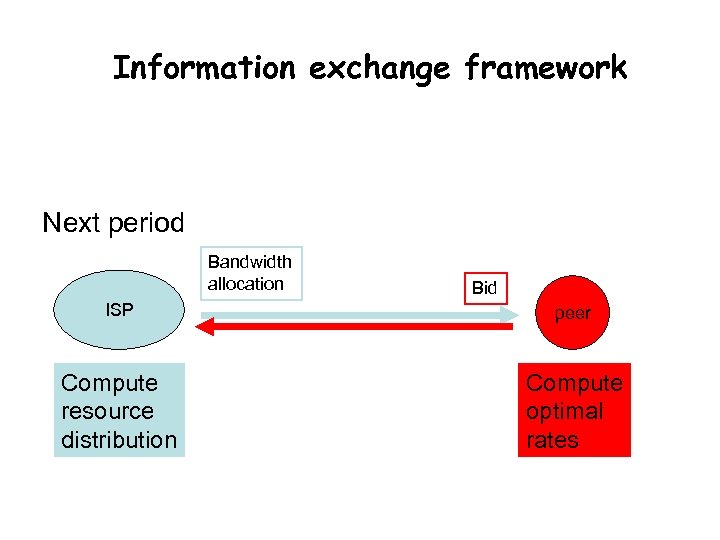
Information exchange framework Next period Bandwidth allocation Bid ISP peer Compute resource distribution Compute optimal rates

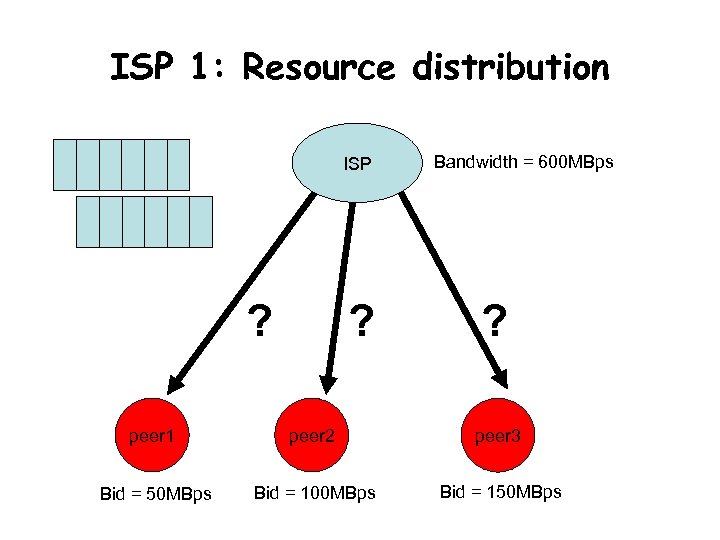
ISP 1: Resource distribution ISP ? ? Bandwidth = 600 MBps ? peer 1 peer 2 peer 3 Bid = 50 MBps Bid = 100 MBps Bid = 150 MBps

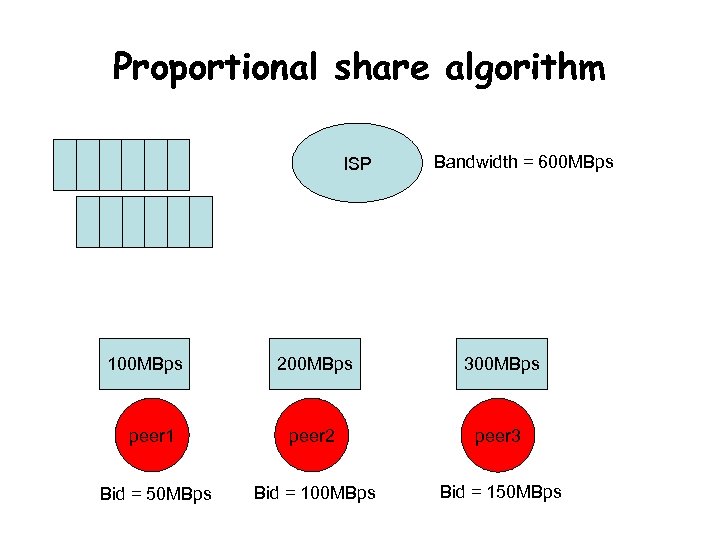
Proportional share algorithm ISP 100 MBps Bandwidth = 600 MBps 200 MBps 300 MBps peer 1 peer 2 peer 3 Bid = 50 MBps Bid = 100 MBps Bid = 150 MBps

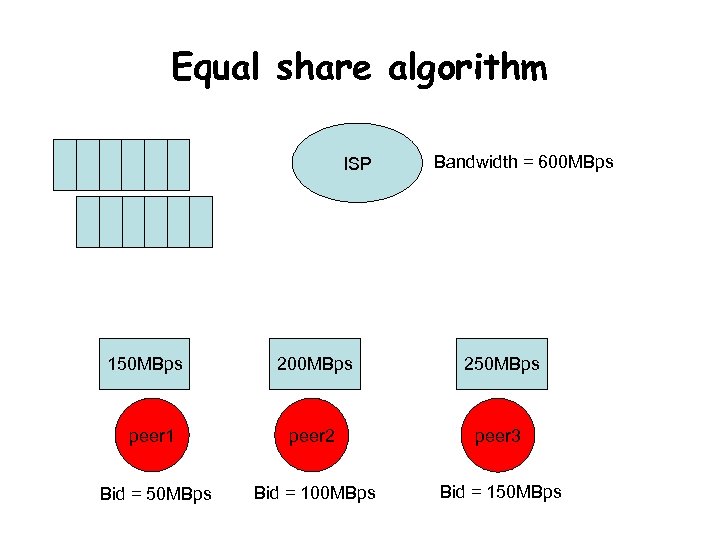
Equal share algorithm ISP 150 MBps Bandwidth = 600 MBps 250 MBps peer 1 peer 2 peer 3 Bid = 50 MBps Bid = 100 MBps Bid = 150 MBps

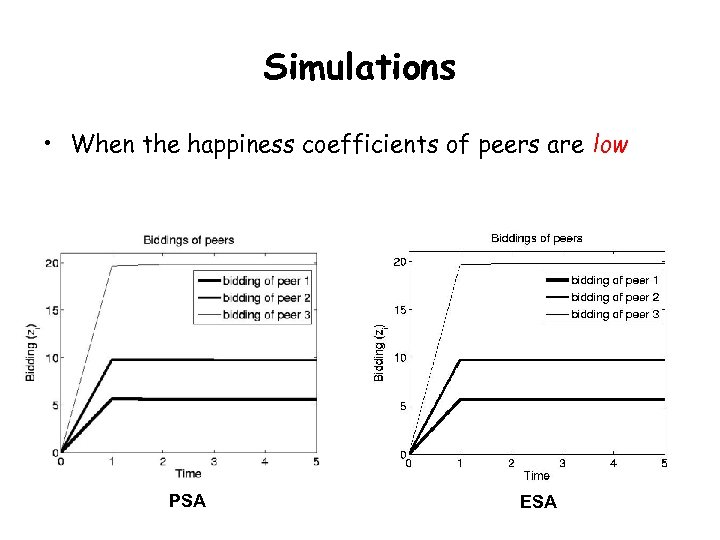
Simulations • When the happiness coefficients of peers are low PSA ESA

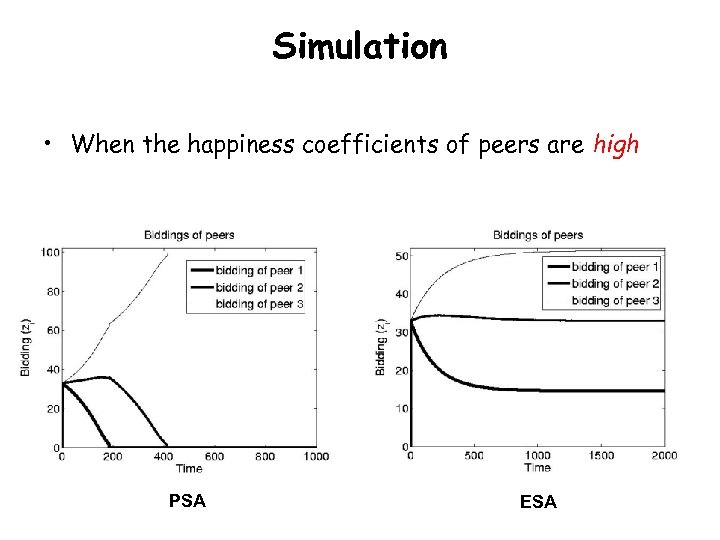
Simulation • When the happiness coefficients of peers are high PSA ESA

ISP 2: Maximization of Revenue Unit price Demand by peer i Total revenue from the peers Determine the optimal price

Solution: Maximization of revenue • Estimate the aggregate traffic ( peers in term of the price (P) ) from all

Conclusions • Utility maximization of a peer • Resource distribution of ISP • Revenue maximization of ISP

Fourth Course On the Access Pricing Issues of Wireless Mesh Networks ICDCS 2006 Ray K. Lam Dah-Ming Chiu John C. S. Lui

WMN Paints a Bright Future • Wireless mesh network (WMN) – Wireless nodes – Multi-hop routing – Form a wireless “mesh” • More access to the Internet – More people, rich or poor – More ubiquitous, anywhere, anytime – More opportunities to everyone Internet

The Critical Thing—Cooperation n. Multi-hop routing n. Relay packets for each other n. My concerns: bandwidth, CPU time, security… n. Community network with symmetric traffic n. Help each other => mutual benefit n. Access network with asymmetric traffic n. Geographically good VS poor n. Why help the poor? n. Incentive system needed—pricing

When AP Meets a Client • Simple analysis by Musacchio and Walrand [1] • A game with 2 players – Access point (AP) provides Internet access – Client buys the service – One deal per time slot AP Client p 1 accept slot 1 p 2 service duration accept slot 2 p 3 reject slot 3 p AP Client

A Beautiful Equilibrium • AP and client each maximizes her gain – AP: guess the “right” price – Client: compare the price p with service utility U • Web browsing utility function • A beautiful equilibrium – AP has the same optimal price in every time slot – Client connects if her per-slot service utility is greater than slot price (U > p) • Encourages flat-rate pricing

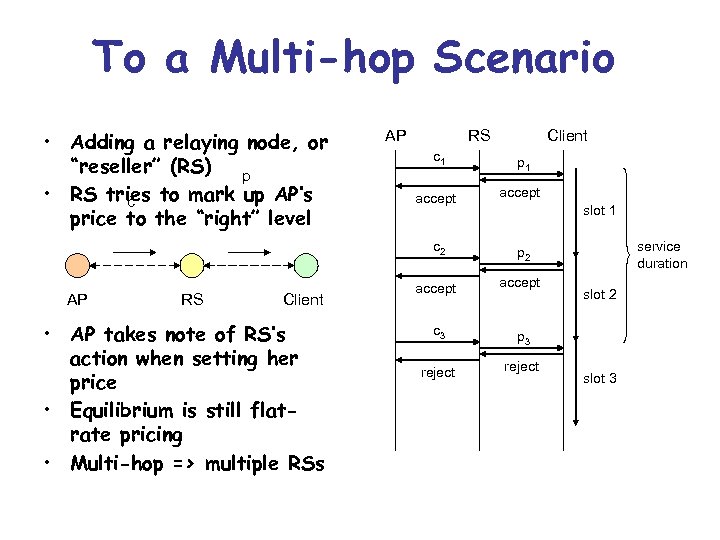
To a Multi-hop Scenario • Adding a relaying node, or “reseller” (RS) p • RS tries to mark up AP’s c price to the “right” level AP RS Client • AP takes note of RS’s action when setting her price • Equilibrium is still flatrate pricing • Multi-hop => multiple RSs p 1 accept c 2 AP c 1 p 2 accept c 3 p 3 reject slot 1 service duration slot 2 slot 3

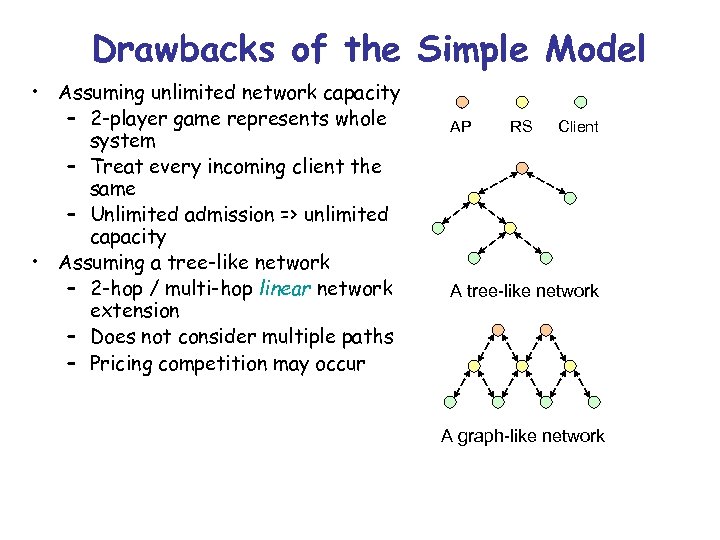
Drawbacks of the Simple Model • Assuming unlimited network capacity – 2 -player game represents whole system – Treat every incoming client the same – Unlimited admission => unlimited capacity • Assuming a tree-like network – 2 -hop / multi-hop linear network extension – Does not consider multiple paths – Pricing competition may occur AP RS Client A tree-like network A graph-like network

What If Capacity Limited? • Cannot admit unlimited clients – Client demands bandwidth guarantee – AP admission control – AP’s system capacity: m • 2 -player game not enough – AP deals with each client differently – Client arrival model: Poisson process • Like an M/M/m/m/M queuing system

Flat-rate Pricing Fails… • Failure scenario – – – AP is full; m clients admitted An admitted client a is paying $5/slot A new client b arrives AP asks b for $6/slot If b accepts • AP raises price for a to $6/slot, OR • Simply kicks a out • Flat-rate pricing is not optimal!

Everybody Loves Flat Rate • Unrealistic for variable rate • More practical—fixed-rate, noninterrupted service – AP charges a client a fixed rate p over time – AP cannot disconnect a client unilaterally • AP can still charge different clients at different “fixed” rates – How to set the optimal rate on different occasions?

Best Strategy in New Service Model • AP sets price based on remaining capacity – Raises price when becoming full – State price: at state k, AP charges next “to-beadmitted” client at fixed rate pk – Policy of AP characterized by price vector • Client’s best strategy – Connect AP if service utility per unit time > price per unit time (U > p)

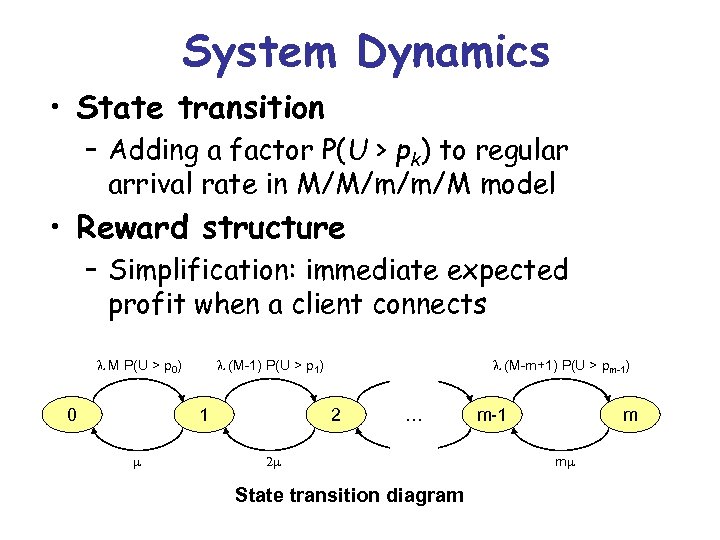
System Dynamics • State transition – Adding a factor P(U > pk) to regular arrival rate in M/M/m/m/M model • Reward structure – Simplification: immediate expected profit when a client connects M P(U > p 0) 0 (M-1) P(U > p 1) 1 (M-m+1) P(U > pm-1) 2 … 2 State transition diagram m-1 m m

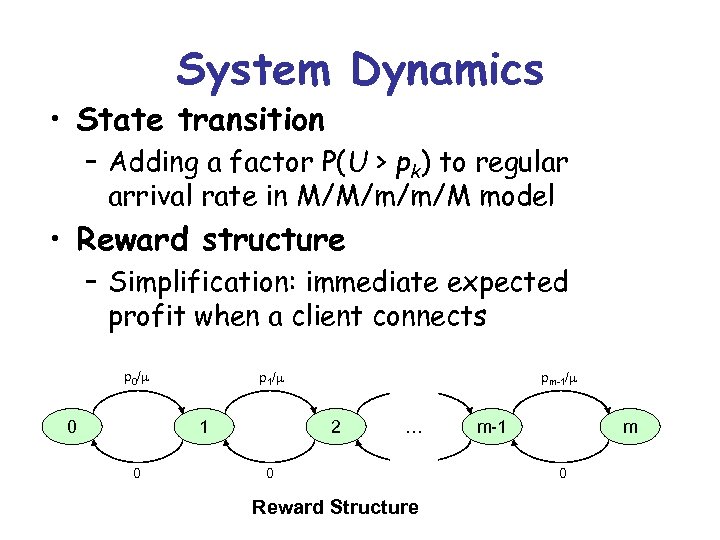
System Dynamics • State transition – Adding a factor P(U > pk) to regular arrival rate in M/M/m/m/M model • Reward structure – Simplification: immediate expected profit when a client connects p 0/ 0 p 1/ 1 0 pm-1/ 2 … 0 Reward Structure m-1 m 0

Finding Optimal Price Vector • Classical optimization – Solution for queuing system gives limiting state probability for each state k, k – Gain of AP is a function of price vector – Complicated to optimize with classical techniques • Policy-iteration method in Markovian decision theory – Reduces computational complexity by iterative algorithm – Guarantees convergence to the best policy

Numerical Results • Capacity m=5, population M=10, departure rate =1 • Vary arrival rate from 0. 2 to 10 • Utility U uniformly distributed on [0, 10] • U normally distributed with mean 5, s. d. 1. 67 • Price increases number of clients in AP and with

Limited Capacity in Multi-hop Case • Simplification – Traffic merges at AP – AP is the bottleneck – Only AP controls admission Internet bandwidth bottleneck AP RS Client • AP’s policy specified by a price matrix – At each state, different prices for requests from different distances – pki: price at state k for a client i-hop away

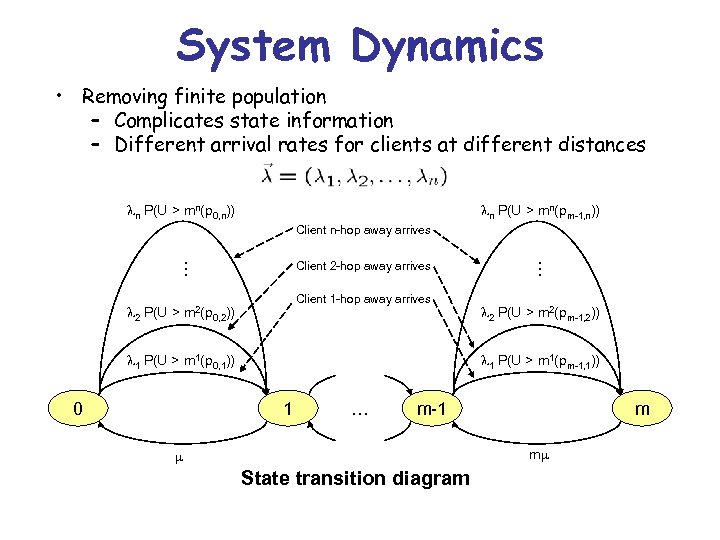
System Dynamics • Removing finite population – Complicates state information – Different arrival rates for clients at different distances n P(U > mn(p 0, n)) n P(U > mn(pm-1, n)) Client n-hop away arrives 2 P(U > m 2(p Client 1 -hop away arrives 0, 2)) 1 P(U > m 1(p 0, 1)) 0 … … Client 2 -hop away arrives 2 P(U > m 2(pm-1, 2)) 1 P(U > m 1(pm-1, 1)) 1 … m-1 m m State transition diagram

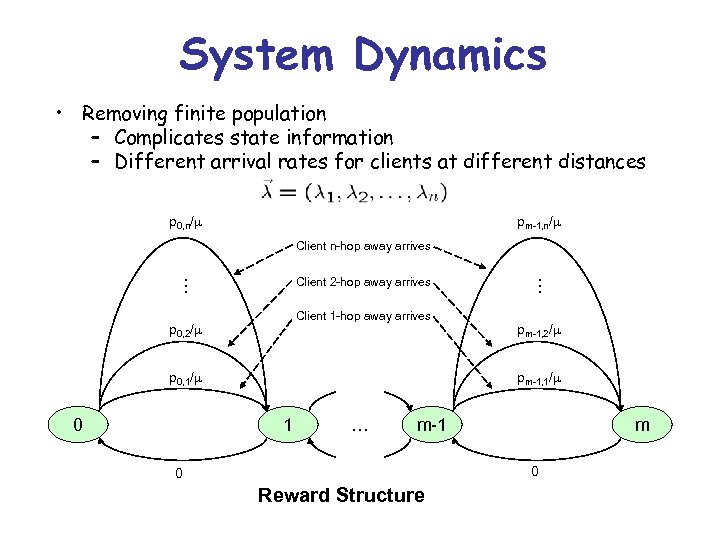
System Dynamics • Removing finite population – Complicates state information – Different arrival rates for clients at different distances p 0, n/ pm-1, n/ Client n-hop away arrives Client 1 -hop away arrives p 0, 2/ p 0, 1/ 0 … … Client 2 -hop away arrives pm-1, 2/ pm-1, 1/ 1 … m-1 m 0 0 Reward Structure

Conclusion • Contributions – – – • Show that fixed-rate pricing fails with limited capacity Generalize unlimited capacity model into limited capacity model Devise optimal pricing for fixed-rate, non-interrupted service with Markovian decision theory References [1] J. Musacchio and J. Walrand. Wi. Fi access point pricing as a dynamic game. IEEE/ACM Trans. Networking. to appear in.