Appendix 5 Additional Applications of Rational Choice and

Appendix 5 Additional Applications of Rational Choice and Demand Theories Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

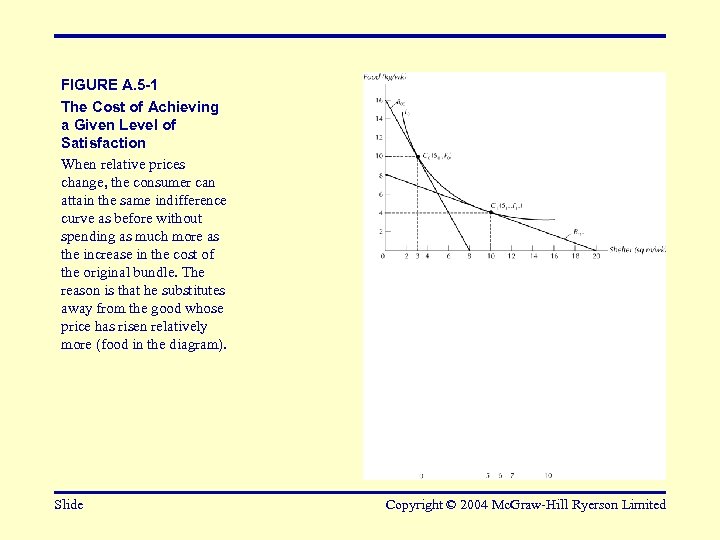FIGURE A. 5 -1 The Cost of Achieving a Given Level of Satisfaction When relative prices change, the consumer can attain the same indifference curve as before without spending as much more as the increase in the cost of the original bundle. The reason is that he substitutes away from the good whose price has risen relatively more (food in the diagram). Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

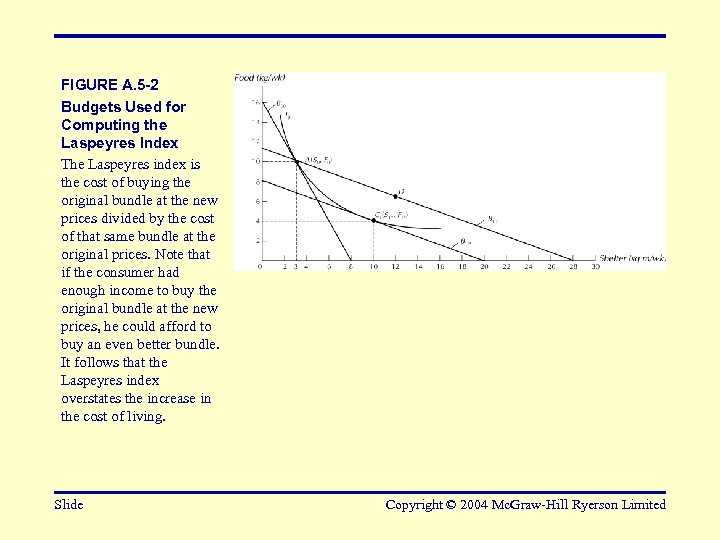FIGURE A. 5 -2 Budgets Used for Computing the Laspeyres Index The Laspeyres index is the cost of buying the original bundle at the new prices divided by the cost of that same bundle at the original prices. Note that if the consumer had enough income to buy the original bundle at the new prices, he could afford to buy an even better bundle. It follows that the Laspeyres index overstates the increase in the cost of living. Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

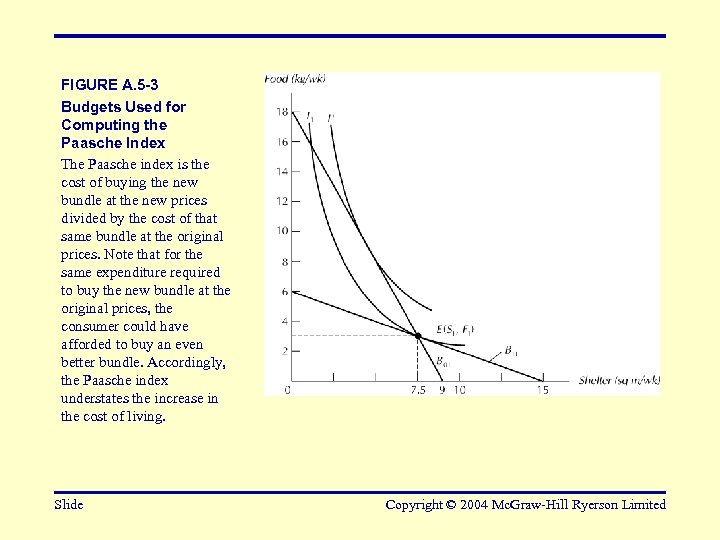FIGURE A. 5 -3 Budgets Used for Computing the Paasche Index The Paasche index is the cost of buying the new bundle at the new prices divided by the cost of that same bundle at the original prices. Note that for the same expenditure required to buy the new bundle at the original prices, the consumer could have afforded to buy an even better bundle. Accordingly, the Paasche index understates the increase in the cost of living. Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

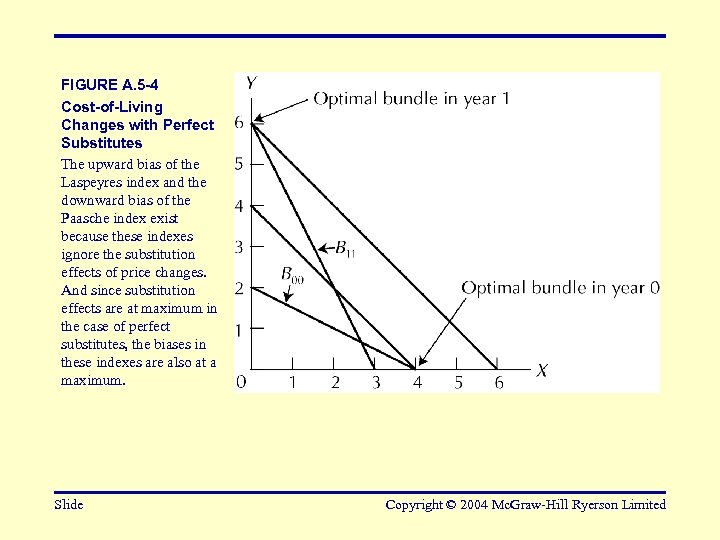FIGURE A. 5 -4 Cost-of-Living Changes with Perfect Substitutes The upward bias of the Laspeyres index and the downward bias of the Paasche index exist because these indexes ignore the substitution effects of price changes. And since substitution effects are at maximum in the case of perfect substitutes, the biases in these indexes are also at a maximum. Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

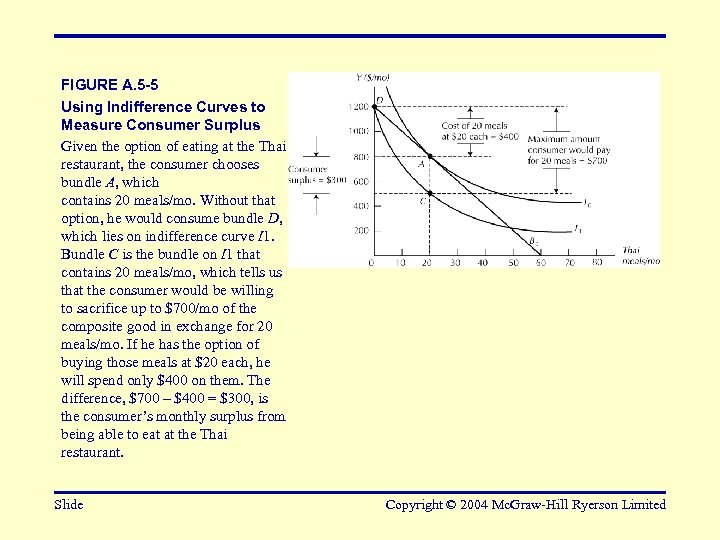FIGURE A. 5 -5 Using Indifference Curves to Measure Consumer Surplus Given the option of eating at the Thai restaurant, the consumer chooses bundle A, which contains 20 meals/mo. Without that option, he would consume bundle D, which lies on indifference curve I 1. Bundle C is the bundle on I 1 that contains 20 meals/mo, which tells us that the consumer would be willing to sacrifice up to $700/mo of the composite good in exchange for 20 meals/mo. If he has the option of buying those meals at $20 each, he will spend only $400 on them. The difference, $700 – $400 = $300, is the consumer’s monthly surplus from being able to eat at the Thai restaurant. Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

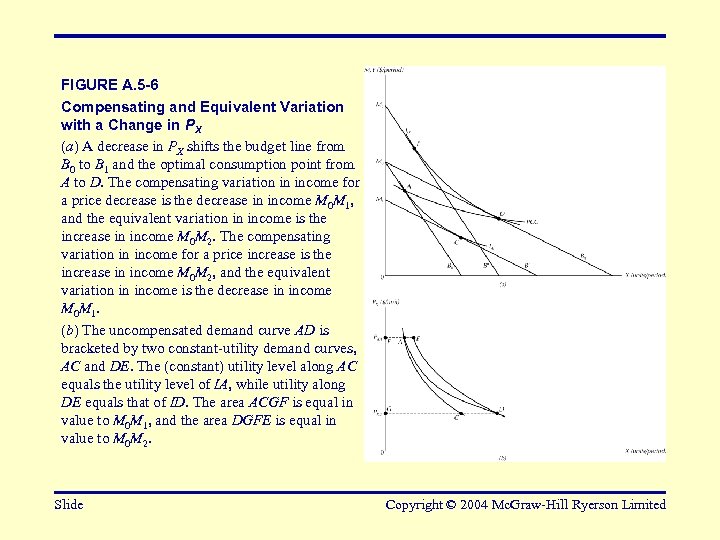FIGURE A. 5 -6 Compensating and Equivalent Variation with a Change in PX (a) A decrease in PX shifts the budget line from B 0 to B 1 and the optimal consumption point from A to D. The compensating variation in income for a price decrease is the decrease in income M 0 M 1, and the equivalent variation in income is the increase in income M 0 M 2. The compensating variation in income for a price increase is the increase in income M 0 M 2, and the equivalent variation in income is the decrease in income M 0 M 1. (b) The uncompensated demand curve AD is bracketed by two constant-utility demand curves, AC and DE. The (constant) utility level along AC equals the utility level of IA, while utility along DE equals that of ID. The area ACGF is equal in value to M 0 M 1, and the area DGFE is equal in value to M 0 M 2. Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

TABLE A. 5 -1 Compensating Variation (C. V. ) and Equivalent Variation (E. V. ) Measures of Consumer Net Benefit: Possible Cases Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited

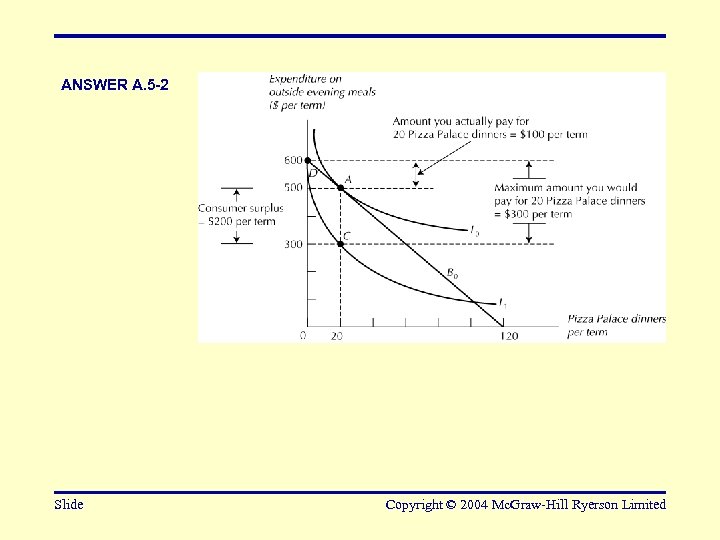ANSWER A. 5 -2 Slide Copyright © 2004 Mc. Graw-Hill Ryerson Limited