AP Physics Chapter 3 Motion in Two Dimensions

AP Physics Chapter 3 Motion in Two Dimensions

Chapter 3: Motion in Two Dimensions 3. 1 3. 2 3. 3 3. 4 Components of Motion Vector Addition and Subtraction Relative Velocity Projectile Motion

Learning Objectives for Chapter 3 • Students should be able to add, subtract, and resolve displacement and velocity vectors so they can: 1. Determine components of a vector along two specified, mutually perpendicular axes. 2. Determine the net displacement of a particle or the location of a particle relative to another. 3. Determine the change in velocity of a particle or the velocity of one particle relative to another. • Students should understand the motion of projectiles in a uniform gravitational field so they can: 1. Write down expressions for the horizontal and vertical components of velocity and position as functions of time, and sketch or identify graphs of these components.

Homework for Chapter 3 • Read Chapter 3 • HW 3. A : pp. 91 -94: 5, 10, 15, 20, 28, 31, 42. • HW 3. B: pp. 94 -96: 50, 52, 55, 58, 61, 68, 69, 76, 78, 79.

Warmup: Read each line aloud without making any mistakes. If you make a mistake you MUST start again without going any further. This is this puzzle This is how puzzle This is to puzzle This is keep puzzle This is a puzzle This is student puzzle This is busy puzzle This is forty puzzle This is seconds! puzzle Now go back and read the THIRD word in each line from the top. http: //www. brainbashers. com

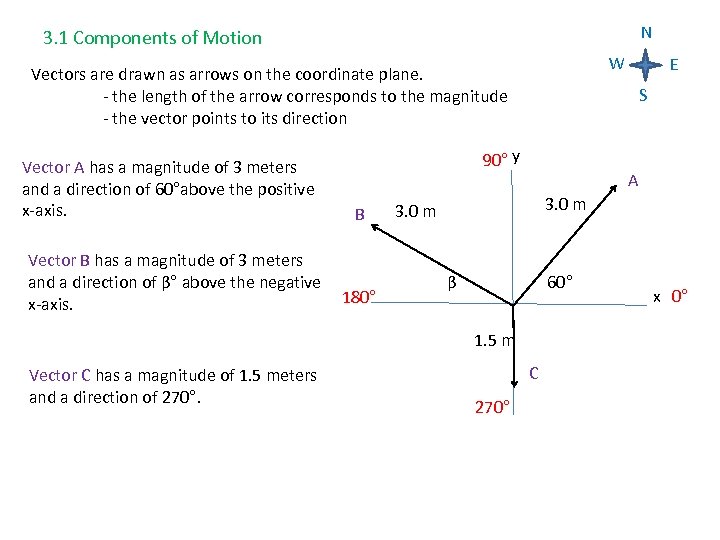N 3. 1 Components of Motion W Vectors are drawn as arrows on the coordinate plane. - the length of the arrow corresponds to the magnitude - the vector points to its direction Vector A has a magnitude of 3 meters and a direction of 60°above the positive x-axis. S 90° y B Vector B has a magnitude of 3 meters and a direction of β° above the negative 180° x-axis. A 3. 0 m 60° β 1. 5 m Vector C has a magnitude of 1. 5 meters and a direction of 270°. E C 270° x 0°

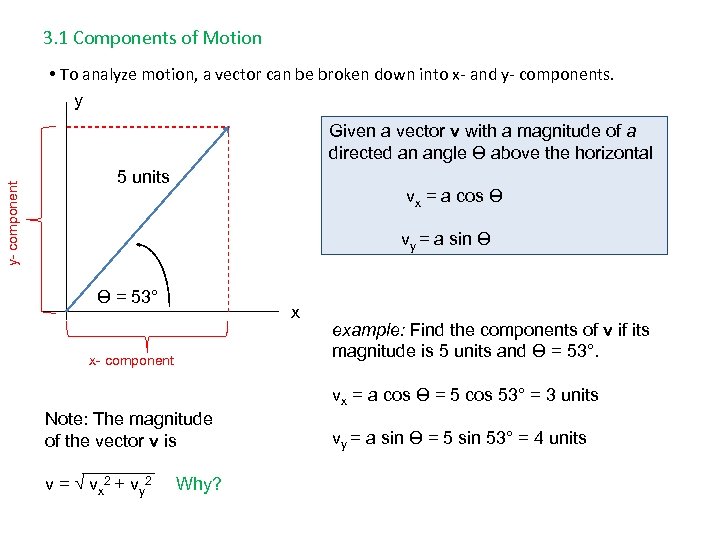3. 1 Components of Motion • To analyze motion, a vector can be broken down into x- and y- components. y y- component Given a vector v with a magnitude of a directed an angle Ө above the horizontal 5 units vx = a cos Ө vy = a sin Ө Ө = 53° x x- component example: Find the components of v if its magnitude is 5 units and Ө = 53°. vx = a cos Ө = 5 cos 53° = 3 units Note: The magnitude of the vector v is v = √ v x 2 + vy 2 Why? vy = a sin Ө = 5 sin 53° = 4 units

3. 1 Components of Motion • Kinematics problems in two-dimensions can be solved by: • resolving the displacement, velocity, and acceleration vectors into their respective components. • using the three constant acceleration equations separately for the x and y directions. • using the Pythagorean theorem to find the magnitude of your resultant vector. • using an inverse trig function to find the angle of your resultant vector

3. 1 Components of Motion Example 1: A boat travels with a speed of 5. 0 m/s in a straight path on a still lake. Suddenly, a steady wind pushes the boat perpendicularly to its straight line path with a speed of 3. 0 m/s for 5. 0 s. Relative to its position just when the wind started to blow, where is the boat at the end of this time? Solution: List givens for x and y directions separately. x-direction vo = 5. 0 m/s a=0 y-direction vo = 3. 0 m/s a=0 Unknowns: x and y Common to both: t = 5. 0 s Analysis: Both motions are motion with constant velocity. Choose the straight path of the boat as the x axis and the direction of the wind as the y axis. Sketch: wind y boat d Ө x

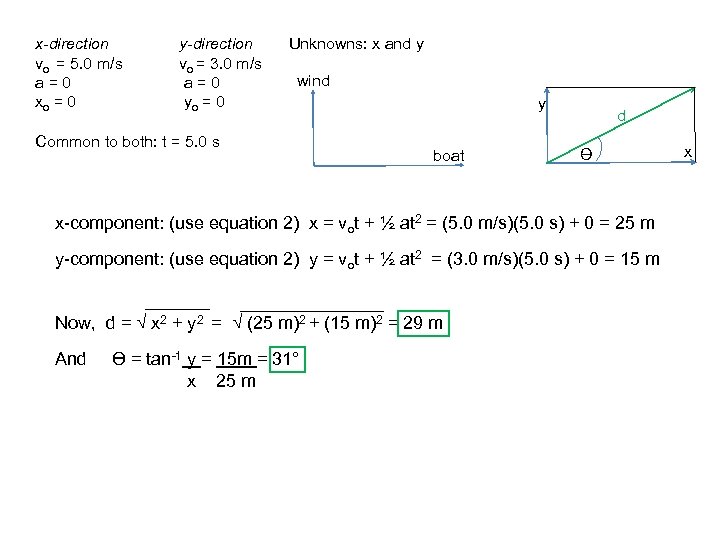x-direction vo = 5. 0 m/s a=0 xo = 0 y-direction vo = 3. 0 m/s a=0 yo = 0 Unknowns: x and y wind Common to both: t = 5. 0 s y boat d Ө x-component: (use equation 2) x = vot + ½ at 2 = (5. 0 m/s)(5. 0 s) + 0 = 25 m y-component: (use equation 2) y = vot + ½ at 2 = (3. 0 m/s)(5. 0 s) + 0 = 15 m Now, d = √ x 2 + y 2 = √ (25 m)2 + (15 m)2 = 29 m And Ө = tan-1 y = 15 m = 31° x 25 m x

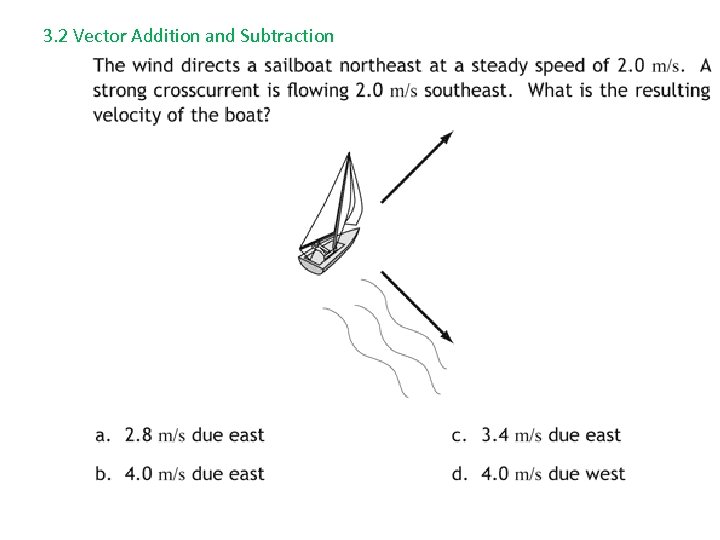
3. 2 Vector Addition and Subtraction vector addition – combining vector quantities by using one of several techniques • geometric methods (triangle, parallelogram, polygon) • vector components and the analytical component method vector subtraction – a special case of vector addition • A - B = A + (-B) • subtracting a vector is the same as adding a negative vector resultant – the overall effect of combining vectors; the vector sum Example: Add vectors A + B + C = R Solution: Use tip-to-tail method

3. 2 Vector Addition and Subtraction • Geometric (Graphical) Methods • use a convenient scale (ex: 1 cm = 10 meters) • To add vectors A and B, draw them tip-to-tail, starting at the origin. • The vector that extends from the tail of A to the tip of B, completing the triangle, is the resultant R = A + B. • When drawn to scale, the magnitude of R can be found by measuring R and using the scale conversion. • Use a protractor to measure the direction of the resultant, ӨR. • You may add on as many vectors as you like; the order doesn’t matter! Example: Add three vectors graphically. Solution:

3. 2 Vector Addition and Subtraction • Analytical (Trigonometry) Method • When vectors make a right triangle with each other, • use the Pythagorean theorem to find the magnitude of your resultant vector. • use the inverse trig function to find the angle of your resultant vector. A = side adjacent to angle Ө O = side opposite to angle Ө H = hypotenuse of triangle H Ө A O SOH – CAH - TOA sin Ө = O A cos Ө = A H tan Ө = O A Ө = sin-1 O A Ө = cos-1 A H Ө = tan-1 O A

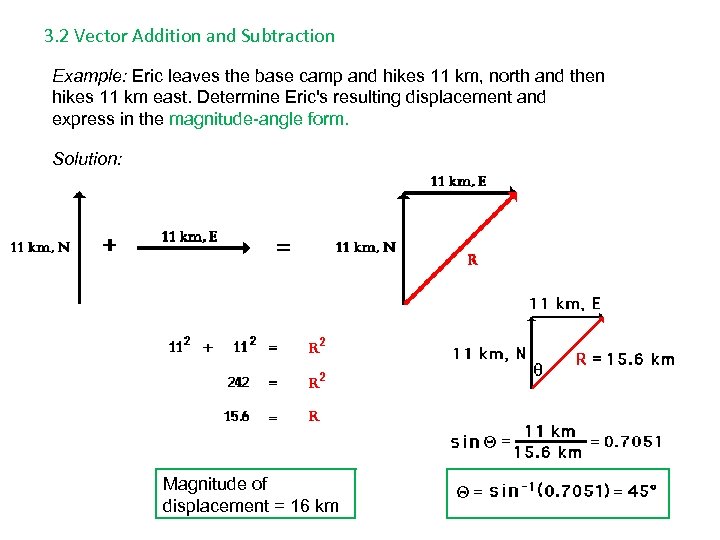3. 2 Vector Addition and Subtraction Example: Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement and express in the magnitude-angle form. Solution: Magnitude of displacement = 16 km

3. 2 Vector Addition and Subtraction

3. 2 Vector Addition and Subtraction

Please Do Now In two minutes, write as many examples of vectors that you can. .

3. 2 Vector Addition and Subtraction Analytical Component Method 1. Resolve the vectors to be added into their x and y components. Include directional signs (plus or minus) in the components. 2. Add, algebraically, all the x- components together and all the y- components together to get the x and y components of the resultant vector. 3. Express the resulting vector using a) The component form using unit vectors , e. g. A = Ax x + Ay y or b) In the magnitude-angle form, e. g. , A = √Ax 2 + Ay 2, Ө = tan-1 Ay Ax unit vector – has a magnitude of one and no units. It indicates a vector’s direction only. 11 km, E ex: R = (11 km) x + (11 km) y 11 km, N R

3. 2 Vector Addition and Subtraction Example: Fred walks 4. 0 km in a direction 60° east of north, then goes 5. 0 km due east. What distance did he walk? What is his displacement?

3. 2 Vector Addition and Subtraction Example: Sheldon and Amy are going to sleep overnight in their tree house and are using some ropes to pull up a box containing their pillows and blankets, which have a total mass of 3. 20 kg. What is the net force on the box? What is its acceleration?

Example: Find the resultant velocity of the sum of v 1 = 35 m/s 30° N of E, and v 2 = 55 m/s 45° N of W N Solution: 1. Resolve the vectors to be added into their x and y components. v 1 x = v 1 cos 30°= (35 m/s) cos 30°= 30. 3 m/s v 1 y = (35 m/s) sin 30°= 17. 5 m/s v 2 v 1 W 45° 30° E N v 2 x = -v 2 cos 45°= (55 m/s) cos 45°= -38. 9 m/s, (-x direction) v 2 y = (55 m/s) sin 45°= 38. 9 m/s v 2. Add components: vx = v 1 x + v 2 x = 30. 3 m/s + (-38. 9 m/s) = -8. 6 m/s vy = v 1 y + v 2 y = 17. 5 m/s + 38. 9 m/s = 56. 4 m/s 3. Express the resultant vector. In component form: v = -8. 6 m/s x + 56 m/s y 56. 4 m/s 81° W In magnitude-angle form: v = √vx 2 + vy 2, = √(-8. 6 m/s)2 + (56. 4 m/s)2 = 57 m/s and Ө = tan-1 vy = tan-1 56. 4 m/s = 81° N of W vx -8. 6 m/s E

Check for Understanding Fill in the blanks using the word bank. magnitude-angle trigonometry component kinematic tip-to-tail components 1. To analyze motion in two dimension, quantities are usually resolved into rectangular _________. 2. Once displacement, velocity, and acceleration vectors are resolved into their respective components, we can apply __________equations. 3. Vectors may be added graphically using the __________method. 4. If your vectors are at right angles, you may use the _______ method. 5. After breaking vectors down into their components, you may perform vector addition by using the analytical _________method. 6. Two ways to express the resultant vector is the ________ form and the component form.

Check for Understanding Fill in the blanks using the word bank. magnitude-angle trigonometry component kinematic tip-to-tail components 1. To analyze motion in two dimension, quantities are usually resolved into rectangular components. 2. Once displacement, velocity, and acceleration vectors are resolved into their respective components, we can apply kinematic equations. 3. Vectors may be added graphically using the tip-to-tail method. 4. If your vectors are at right angles, you may use the trigonometry method. 5. After breaking vectors down into their components, you may perform vector addition by using the analytical component method. 6. Two ways to express the resultant vector is the magnitude-angle form and the component form.

Please Do Now Using full sentences, explain the steps to the analytical component method in your own words.

Homework for Sections 3. 1 -3. 2 • HW 3. A : pp. 91 -94: 5, 10, 11 -12, 15, 20, 28, 31, 42.

Warmup: Decipher each language equation. 1. 1 = E on C One Eye on a Cyclops 2. 1 = G. L. for M. One Giant Leap for Mankind 3. 1 = K. K on the E. S. B One King Kong on the Empire State Building 4. 1 = S. C. in D. P. One Single Calorie in Diet Pepsi 5. 1 = S. S. One Singular Sensation 6. 1 = T. that O. K One Time that Opportunity Knocks 7. 1 = W. on a U. Wheel on a Unicycle 8. 1 = if by L. One if by Land

3. 3 Relative Velocity • “Everything is relative…” • Physical phenomena can be observed from different frames of reference. ex: The velocity of a ball tossed by a passenger in a moving car will be measured differently by a passenger on the car than by an observer on Earth. • Your reference is the origin, or zero point, of your coordinate system. • Any velocity we measure is relative. ex: The velocity of a moving car is measured relative to the ground. ex: The revolving motion of the Earth around the Sun is relative to the Sun. ex: moving sidewalk in an airport • Relative velocity can be determined with vector addition or subtraction. • Standard symbols are used to represent relative velocity. ex: vcg (where c stands for car and g stand for ground) means the velocity of a car relative to the ground.

3. 3 Relative Velocity • When velocities are along a straight line in the same or opposite direction and all have the same reference, we can find relative velocities by vector subtraction. v. AB = v. A – v. B v. AB = - v. BA v. AC = v. AB + v. BC Ex: A student walks on a treadmill moving at 4. 0 m/s and remains at the same place in the gym. a) What is the student’s velocity relative to the gym floor? zero b) What is the student’s speed relative to the treadmill? s = student, t = treadmill, and g = ground Unknown: vst. Knowns: vsg = 0, vtg = -4. 0 m/s. vsg = vst + vtg → vst = vsg – vtg = 0 – (-4. 0 m/s) = 4. 0 m/s c) What is the treadmill’s speed relative to the student? vts = - vst = -4. 0 m/s

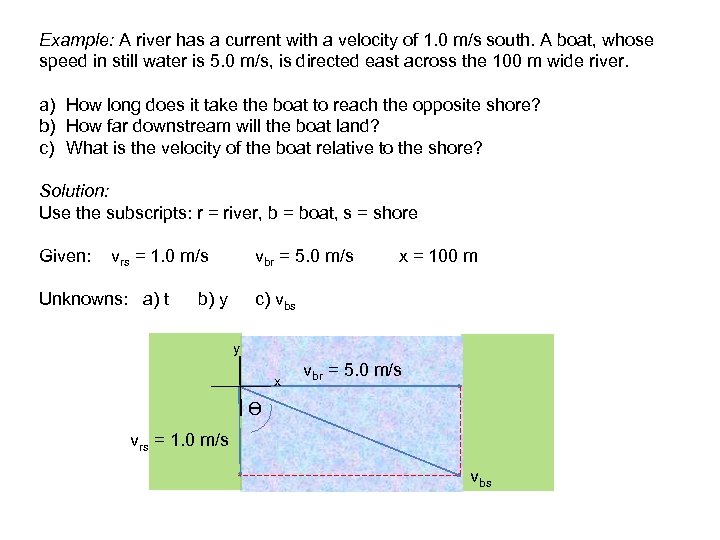Example: A river has a current with a velocity of 1. 0 m/s south. A boat, whose speed in still water is 5. 0 m/s, is directed east across the 100 m wide river. a) How long does it take the boat to reach the opposite shore? b) How far downstream will the boat land? c) What is the velocity of the boat relative to the shore? Solution: Use the subscripts: r = river, b = boat, s = shore Given: vrs = 1. 0 m/s Unknowns: a) t vbr = 5. 0 m/s b) y x = 100 m c) vbs y x vbr = 5. 0 m/s Ө vrs = 1. 0 m/s vbs

a) Use kinematics equation 2: x = xo + vot +1/2 at 2 , where a = 0, xo = 0, vo = vbr, and x = 100 m x= vot → solve for t t = x = 100 m = 20 s vo 5. 0 m/s b) Use kinematics equation 2: y = yo + vot +1/2 at 2 , where a = 0, yo = 0, vo = vrs y = vot = (1. 0 m/s)(20 s) = 20 m c) The velocity of the boat relative to shore is the vector sum of the velocity of the boat relative to the river and the velocity of the river relative to the shore (current) vbs = vbr + vrs *Hint: the pattern of subscripts are helpful in problem solving. On the right side of the equation, the two inner subscripts are the same (r). The outer subscripts (b and s) are sequentially the same as those for the relative velocity on the left side of the equation. *** vbs = √vbr 2+ vrs 2 = √(5. 0 m/s)2 + (1. 0 m/s)2 = 5. 1 m/s Ө = tan-1 5. 0 m/s 1. 0 m/s = 79° measured from the shoreline.

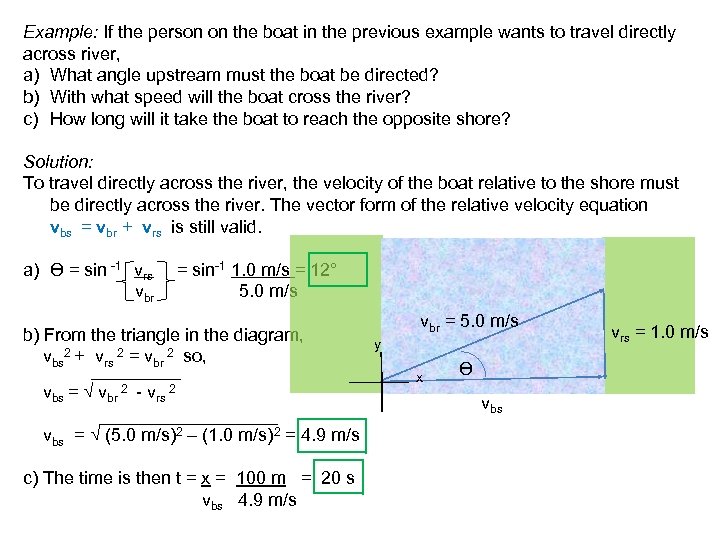Example: If the person on the boat in the previous example wants to travel directly across river, a) What angle upstream must the boat be directed? b) With what speed will the boat cross the river? c) How long will it take the boat to reach the opposite shore? Solution: To travel directly across the river, the velocity of the boat relative to the shore must be directly across the river. The vector form of the relative velocity equation vbs = vbr + vrs is still valid. a) Ө = sin -1 vrs vbr = sin-1 1. 0 m/s = 12° 5. 0 m/s b) From the triangle in the diagram, vbs 2 + vrs 2 = vbr 2 so, vbs = √ vbr 2 - vrs 2 vbs = √ (5. 0 m/s)2 – (1. 0 m/s)2 = 4. 9 m/s c) The time is then t = x = 100 m = 20 s vbs 4. 9 m/s vbr = 5. 0 m/s y x Ө vbs vrs = 1. 0 m/s

3. 4 Projectile Motion projectile – an object upon which the only force is gravity. The key to projectile motion problems is recognizing the vertical and horizontal components of motion are independent. • The vertical motion, or y- component is free fall, so a = -9. 80 m/s 2 • The horizontal motion, or x- component, has zero acceleration. Why? • Time is the common factor, and can be use to link the two equations. Use kinematics equations 1 & 2 for the y- direction: vy = vyo + a t y = yo + vyo t + ½ ay t 2 Use the same equations for the x- direction: vx = vxo t

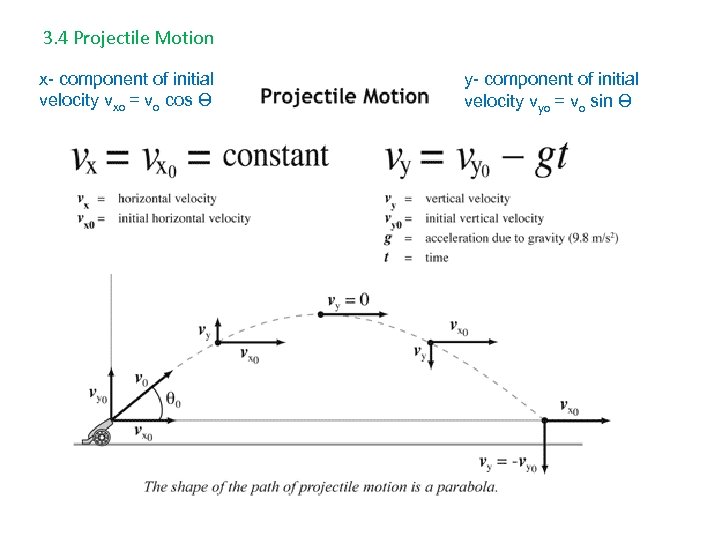3. 4 Projectile Motion x- component of initial velocity vxo = vo cos Ө y- component of initial velocity vyo = vo sin Ө

Example: A package is dropped from an airplane traveling with a constant horizontal speed of 120 m/s at an altitude of 500 m. What is the horizontal distance the package travels before hitting the ground (range)? Solution: Given: horizontal motion vxo = 120 m/s vertical motion vyo = 0 y = -500 m y vo = vxo x 500 m Find: range Since the range is given by x = vxo t , we have to find the time of flight t first. From the vertical motion, we use y = vyot + ½ ayt 2 So, -500 m = 0 + ½ (-9. 80 m/s 2) t 2, solving, t = 10. 1 s Therefore, x = (120 m/s)(10. 1 s) = 1. 21 x 103 m = 1. 21 km Hint: The quantities such as initial velocities and displacements have to be treated independently. For example, the initial horizontal velocity is 120 m/s and the initial vertical velocity is zero. The 12. 0 m/s can only be used in the horizontal motion and the 0 m/s can only be used in the vertical motion. A common mistake is to mix up these quantities or not treat them as independent.

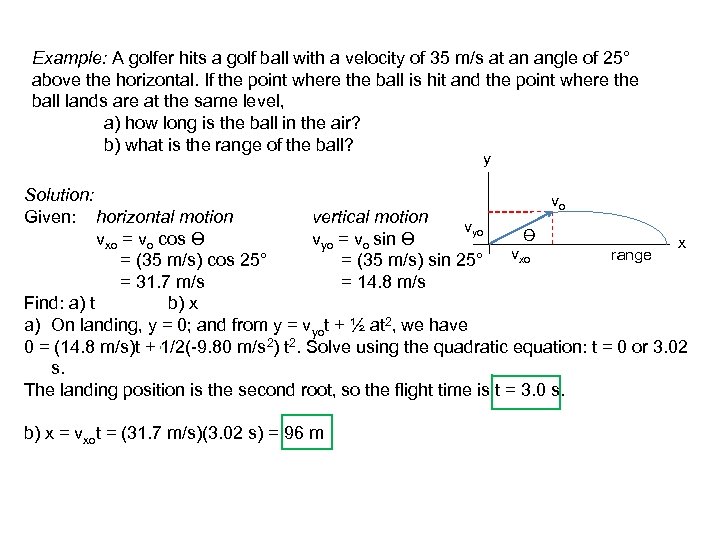Example: A golfer hits a golf ball with a velocity of 35 m/s at an angle of 25° above the horizontal. If the point where the ball is hit and the point where the ball lands are at the same level, a) how long is the ball in the air? b) what is the range of the ball? y Solution: vo Given: horizontal motion vertical motion vyo Ө vxo = vo cos Ө vyo = vo sin Ө x vxo range = (35 m/s) cos 25° = (35 m/s) sin 25° = 31. 7 m/s = 14. 8 m/s Find: a) t b) x a) On landing, y = 0; and from y = vyot + ½ at 2, we have 0 = (14. 8 m/s)t + 1/2(-9. 80 m/s 2) t 2. Solve using the quadratic equation: t = 0 or 3. 02 s. The landing position is the second root, so the flight time is t = 3. 0 s. b) x = vxot = (31. 7 m/s)(3. 02 s) = 96 m

Check for Understanding:

vy = vyo + at ; vy = 0 at peak. x = vxo t

Homework for Section 3. 4 • HW 3. B: pp. 94 -96: 50, 52, 55, 58, 61, 68, 69, 76, 78, 79.