AOE 5104 Class 10 Online presentations for

AOE 5104 Class 10 • Online presentations for next class: – Potential Flow 1 • Homework 4 due 10/2

Kinematics of Vorticity

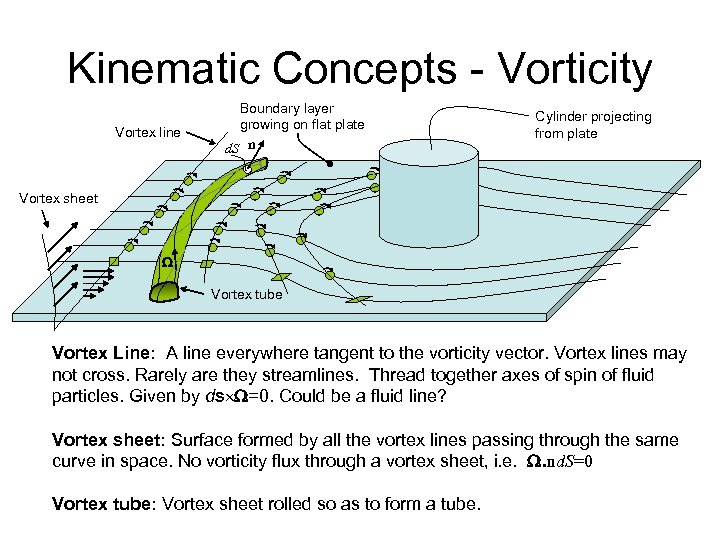Kinematic Concepts - Vorticity Vortex line Boundary layer growing on flat plate d. S n Cylinder projecting from plate Vortex sheet Vortex tube Vortex Line: A line everywhere tangent to the vorticity vector. Vortex lines may not cross. Rarely are they streamlines. Thread together axes of spin of fluid particles. Given by ds =0. Could be a fluid line? Vortex sheet: Surface formed by all the vortex lines passing through the same curve in space. No vorticity flux through a vortex sheet, i. e. . nd. S=0 Vortex tube: Vortex sheet rolled so as to form a tube.

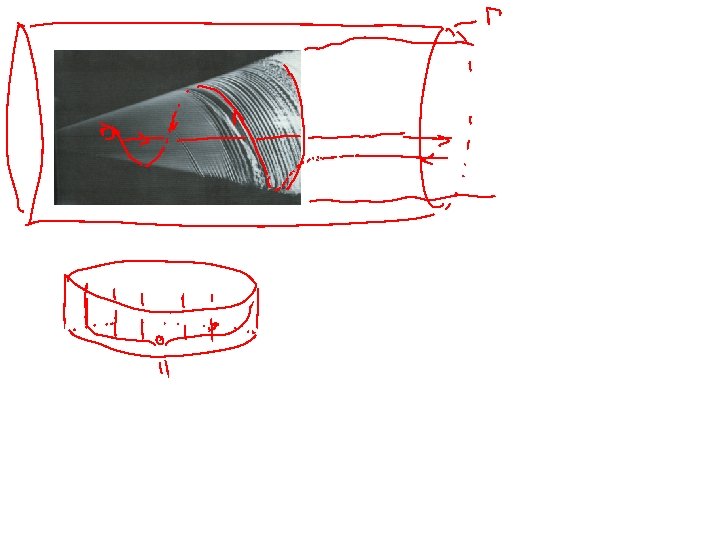
Spinning Cone Spiral vortices formed on a 20 cm-wide spinning cone at 2. 9 m/s. Boundary layer is revealed.

Implications (Helmholtz’ Vortex Theorems, Part 1) • The strength of a vortex tube (defined as the circulation around it) is constant along the tube. • The tube, and the vortex lines from which it is composed, can therefore never end. They must extend to infinity or form loops. • The average vorticity magnitude inside a vortex tube is inversely proportional to the crosssectional area of the tube

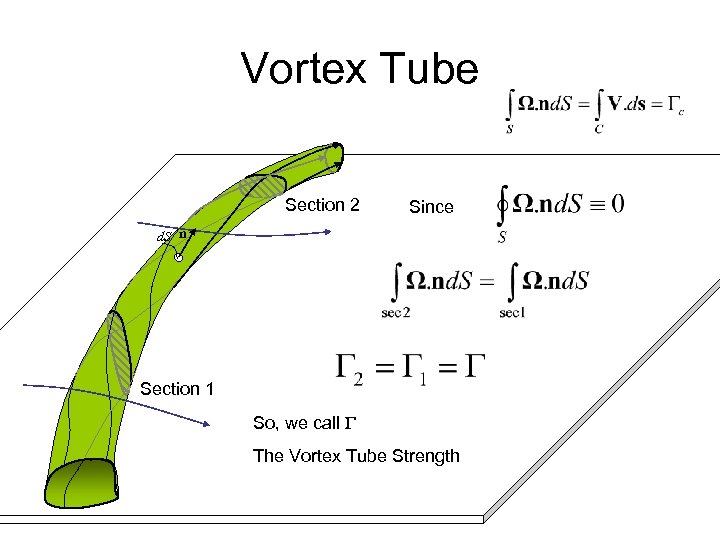Vortex Tube Section 2 Since d. S n Section 1 So, we call The Vortex Tube Strength

Implications (Helmholtz’ Vortex Theorems, Part 1) • The strength of a vortex tube (defined as the circulation around it) is constant along the tube. • The tube, and the vortex lines from which it is composed, can therefore never end. They must extend to infinity or form loops. • The average vorticity magnitude inside a vortex tube is inversely proportional to the crosssectional area of the tube

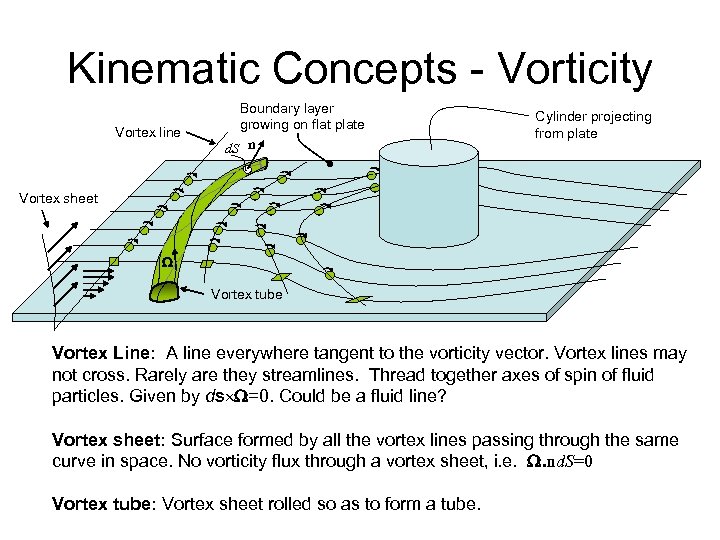Kinematic Concepts - Vorticity Vortex line Boundary layer growing on flat plate d. S n Cylinder projecting from plate Vortex sheet Vortex tube Vortex Line: A line everywhere tangent to the vorticity vector. Vortex lines may not cross. Rarely are they streamlines. Thread together axes of spin of fluid particles. Given by ds =0. Could be a fluid line? Vortex sheet: Surface formed by all the vortex lines passing through the same curve in space. No vorticity flux through a vortex sheet, i. e. . nd. S=0 Vortex tube: Vortex sheet rolled so as to form a tube.

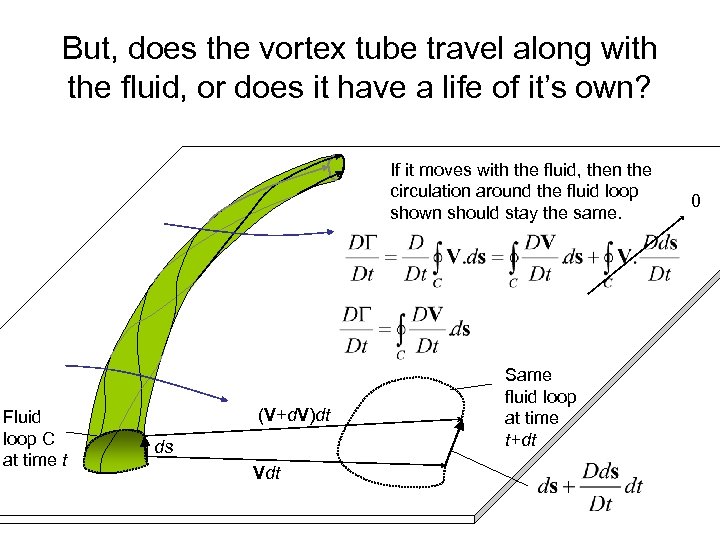But, does the vortex tube travel along with the fluid, or does it have a life of it’s own? If it moves with the fluid, then the circulation around the fluid loop shown should stay the same. Fluid loop C at time t (V+d. V)dt ds Vdt Same fluid loop at time t+dt 0

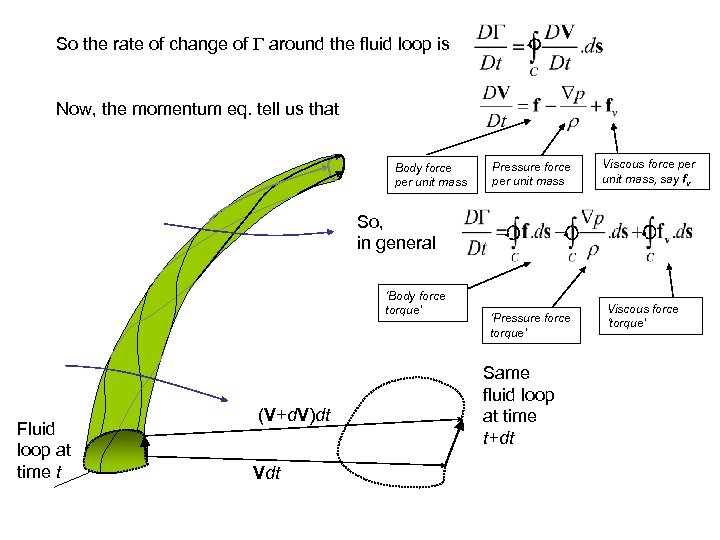So the rate of change of around the fluid loop is Now, the momentum eq. tell us that Body force per unit mass Pressure force per unit mass Viscous force per unit mass, say fv So, in general ‘Body force torque’ Fluid loop at time t (V+d. V)dt Vdt ‘Pressure force torque’ Same fluid loop at time t+dt Viscous force ‘torque’

Body Force Torque Stokes Theorem For gravity So, body force torque is zero for gravity and for any irrotational body force field Therefore, body force torque is zero for most practical situations

Pressure Force Torque If density is constant So, pressure force torque is zero. Also true as long as = (p). Pressure torques generated by • Curved shocks • Free surface / stratification

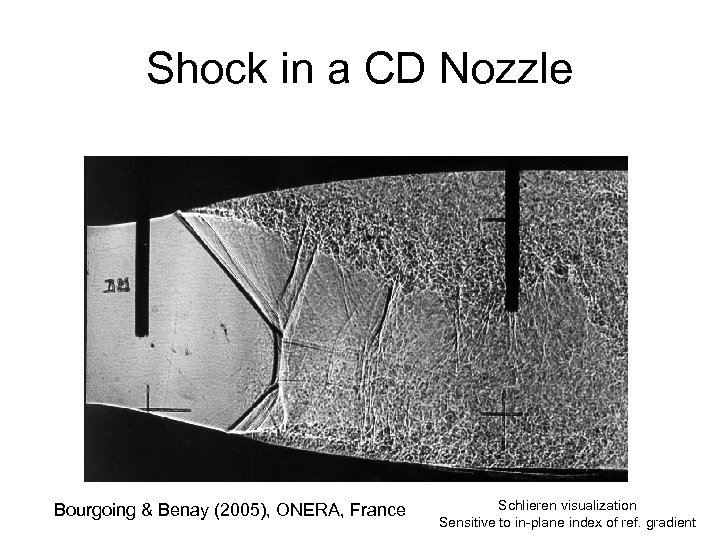Shock in a CD Nozzle Bourgoing & Benay (2005), ONERA, France Schlieren visualization Sensitive to in-plane index of ref. gradient

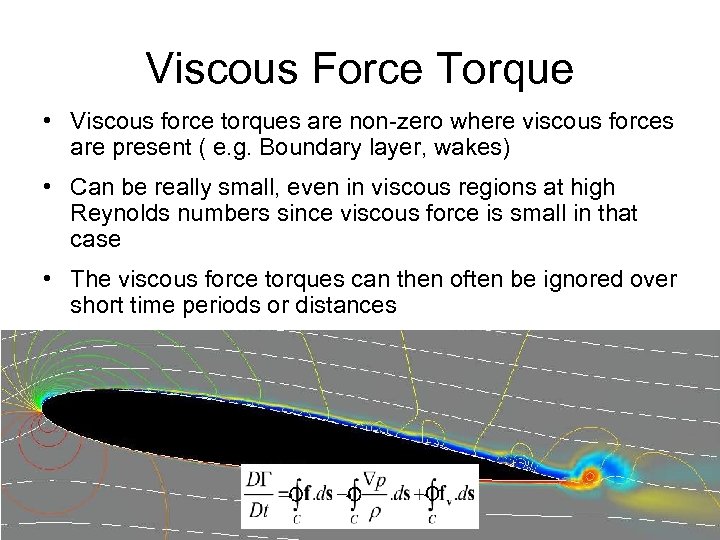Viscous Force Torque • Viscous force torques are non-zero where viscous forces are present ( e. g. Boundary layer, wakes) • Can be really small, even in viscous regions at high Reynolds numbers since viscous force is small in that case • The viscous force torques can then often be ignored over short time periods or distances

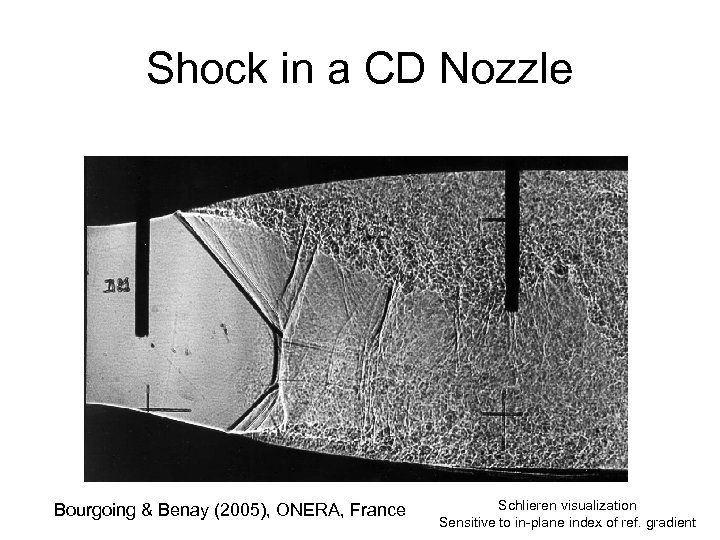Shock in a CD Nozzle Bourgoing & Benay (2005), ONERA, France Schlieren visualization Sensitive to in-plane index of ref. gradient

Implications In the absence of body-force torques, pressure torques and viscous torques… • the circulation around a fluid loop stays constant: Kelvin’s Circulation Theorem • a vortex tube travels with the fluid material (as though it were part of it), or – – a vortex line will remain coincident with the same fluid line the vorticity convects with the fluid material, and doesn’t diffuse fluid with vorticity will always have it fluid that has no vorticity will never get it Helmholtz’ Vortex Theorems, Part 2 ‘Body force torque’ ‘Pressure force torque’ Viscous force ‘torque’

Lord Kelvin (1824 -1907) (William Thompson )

Vorticity Transport Equation • The kinematic condition for convection of vortex lines with fluid lines is found as follows After a lot of math we get. .

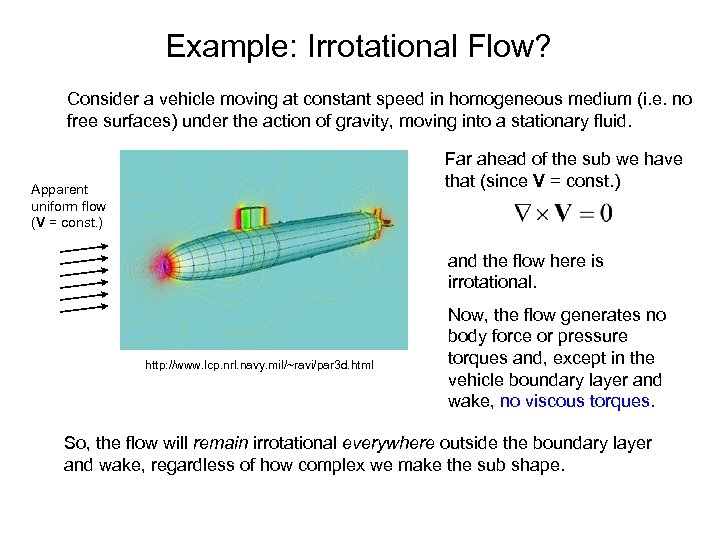Example: Irrotational Flow? Consider a vehicle moving at constant speed in homogeneous medium (i. e. no free surfaces) under the action of gravity, moving into a stationary fluid. Far ahead of the sub we have that (since V = const. ) Apparent uniform flow (V = const. ) and the flow here is irrotational. http: //www. lcp. nrl. navy. mil/~ravi/par 3 d. html Now, the flow generates no body force or pressure torques and, except in the vehicle boundary layer and wake, no viscous torques. So, the flow will remain irrotational everywhere outside the boundary layer and wake, regardless of how complex we make the sub shape.

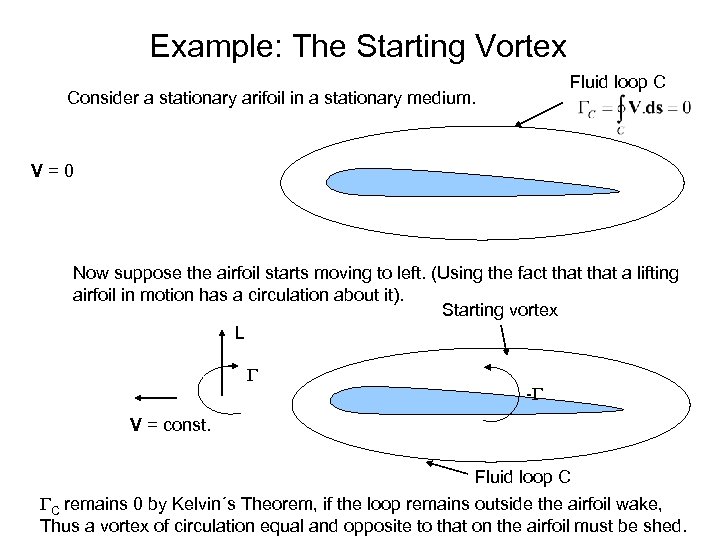Example: The Starting Vortex Fluid loop C Consider a stationary arifoil in a stationary medium. V=0 Now suppose the airfoil starts moving to left. (Using the fact that a lifting airfoil in motion has a circulation about it). Starting vortex L - V = const. Fluid loop C C remains 0 by Kelvin´s Theorem, if the loop remains outside the airfoil wake, Thus a vortex of circulation equal and opposite to that on the airfoil must be shed.

Starting Vortex Pictures are from “An Album of Fluid Motion” by Van Dyke

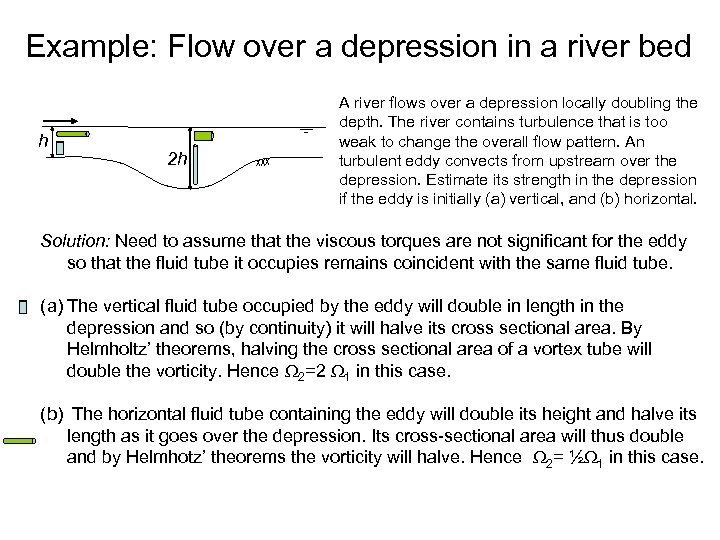Example: Flow over a depression in a river bed h 2 h A river flows over a depression locally doubling the depth. The river contains turbulence that is too weak to change the overall flow pattern. An turbulent eddy convects from upstream over the depression. Estimate its strength in the depression if the eddy is initially (a) vertical, and (b) horizontal. Solution: Need to assume that the viscous torques are not significant for the eddy so that the fluid tube it occupies remains coincident with the same fluid tube. (a) The vertical fluid tube occupied by the eddy will double in length in the depression and so (by continuity) it will halve its cross sectional area. By Helmholtz’ theorems, halving the cross sectional area of a vortex tube will double the vorticity. Hence 2=2 1 in this case. (b) The horizontal fluid tube containing the eddy will double its height and halve its length as it goes over the depression. Its cross-sectional area will thus double and by Helmhotz’ theorems the vorticity will halve. Hence 2= ½ 1 in this case.

The River Avon nearing flood stage, Salisbury, Wiltshire, UK

Example: Evolution of turbulence in a shear flow U=ky, k=const y Turbulence is convected and distorted in a shear flow, as shown. Consider an eddy that at time t=0 is vertically aligned and has a vorticity o. Estimate the vorticity magnitude and angle of an eddy, as functions of time. Solution: Need to assume that the viscous torques are not significant for the eddy so that the fluid tube it occupies remains coincident with the same fluid tube. Also need too assume that the eddy is to weak to influence the flow that is convecting it. Consider a segment of the eddy of length l. In time t the top of the eddy will y l convect further than the bottom by an amount equal to the difference in the Time 0 velocity (kl) times the time. The angle of the fluid tube containing the eddy will thus be klt Time t The fluid tube also grows longer by the factor The cross sectional area of the tube thus reduces by this factor, and therefore the vorticity increases by this factor, i. e.

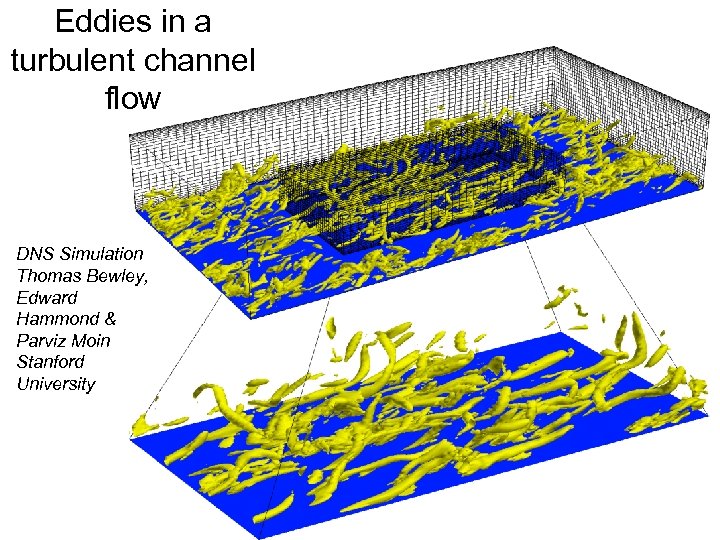Eddies in a turbulent channel flow DNS Simulation Thomas Bewley, Edward Hammond & Parviz Moin Stanford University

Example: Flow around a corner in a channel 6 o Air flows through a duct with a 6 o corner. An initially vertical eddy is introduced into the otherwise uniform flow upstream and convects around the corner. Estimate its orientation downstream. Solution: Need to assume that the viscous torques are not significant for the eddy so that the fluid tube it occupies remains coincident with the same fluid tube, and so that no vorticity is generated in the turn. Also need to assume that the eddy is too weak to influence the flow that is convecting it. Consider two initially perpendicular fluid lines, one in the streamwise direction and one vertical, coincident with the eddy. Since there is no vorticity component perpendicular to the page, and no torques to generate any, the sum of the rotation rates of these two fluid lines must remain zero. o 6 The streamwise fluid line will follow the streamline and thus rotate counterclockwise by 6 o. The vertical fluid line and thus the eddy must therefore rotate clockwise by 6 o, as shown. 6 o

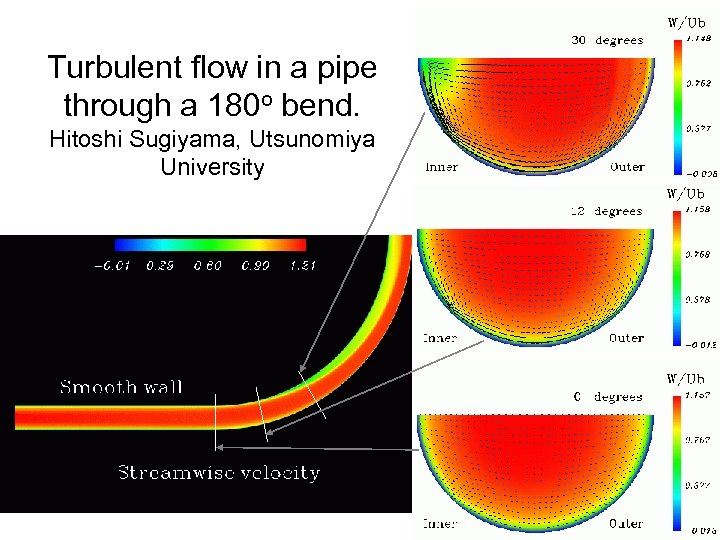Turbulent flow in a pipe through a 180 o bend. Hitoshi Sugiyama, Utsunomiya University

Ox Bows