Ансамбли квантовых частиц 57. Ансамбли квантовых частиц. Принцип тождественности частиц. 58. Симметричные и антисимметричные состояния микрочастиц. 59. Квантовые системы частиц Бозе и частиц Ферми.
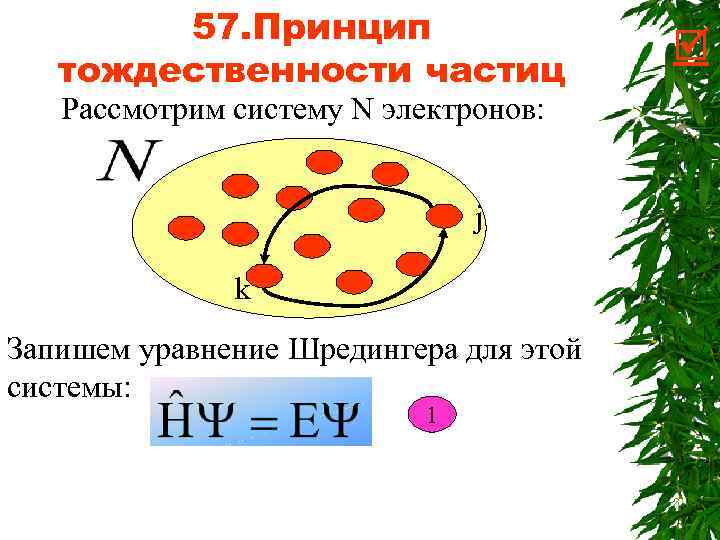
57. Принцип тождественности частиц Рассмотрим систему N электронов: j k Запишем уравнение Шредингера для этой системы: 1
Гамильтониан: Введем оператор перестановки Принцип тождественности: при перестановки частиц местами изменений нет, энергия при этом не меняется, так как все частицы одинаковы. Но эта тождественность приводит к некоторым последствиям.
Оператор перестановки и гамильтониан коммутируют, то есть: Подействуем оператором на уравнение Шредингера:
При перестановке частиц местами получается другое состояние, но энергия не меняется. То есть состояния разные но энергия одна и та же
58. Симметричные и антисимметричные состояния микрочастиц Произведем перестановку два раза. Вторая перестановка дает ту же функцию: - оператор перестановки
То есть Квантовое уравнение дает два решения: -симметричное состояние (s) -антисимметричное состояние (а) Если при перестановке знак волновой функции не меняется, то такое состояние называется симметричным состоянием (s) Можно показать, что между этими состояниями и переходов нет !!!
-симметричное состояние (s) -антисимметричное состояние (а) Пусть в начальный момент времени (при t=0) волновая функция описывает симметричное состояние Посмотрим, что даст уравнение Шредингера:
Действуем оператором перестановки на обе части уравнения:
Приращение симметричной функции является симметричным.
Аналогично для антисимметрич ного случая получим: Приращение антисимметричной функции антисимметрично То есть, переходов между нет!!!
59. Квантовые системы частиц Бозе и частиц Ферми. Исходя из опытных данных физики договорились считать, что частицы подчиняются статистике. для систем Бозе – Эйнштейна (бозоны): I волновые функции симметричны , спин всегда целый S=0, 1, 2, 3, …;
Пример: 2 частицы: 1 и 2 в состояниях a и b, волновые функции Полную волновую функцию можно составить тремя способами: 1 2 3
II для систем Ферми – Дирака (фермионы) волновые функции антисимметричны , спин всегда полуцелый Здесь существует принцип запрета Паули: в данной системе в одном и том же квантовом состоянии не может находиться более одной частицы. Этот принцип приближенный.
Пример: 2 частицы: 1 и 2 в состояниях a и b, волновые функции Легко проверить:
Вопросы ? Что такое ансамбли частиц? ? В чем заключается принцип тождественности частиц? ? Сущность запрета Паули. ? Опишите системы частиц Бозе. ? Опишите системы частиц Ферми.
Скачать презентацию Ансамбли квантовых частиц 57 Ансамбли квантовых частиц Принцип
11.Ансамбли квантовых частиц..ppt