8a9ab5820bcf1818eae7ae107d163a7c.ppt
- Количество слайдов: 17
 Announcements: • Homework 10: – Due next Thursday (4/25) – Assignment will be on the web by tomorrow night.
Announcements: • Homework 10: – Due next Thursday (4/25) – Assignment will be on the web by tomorrow night.
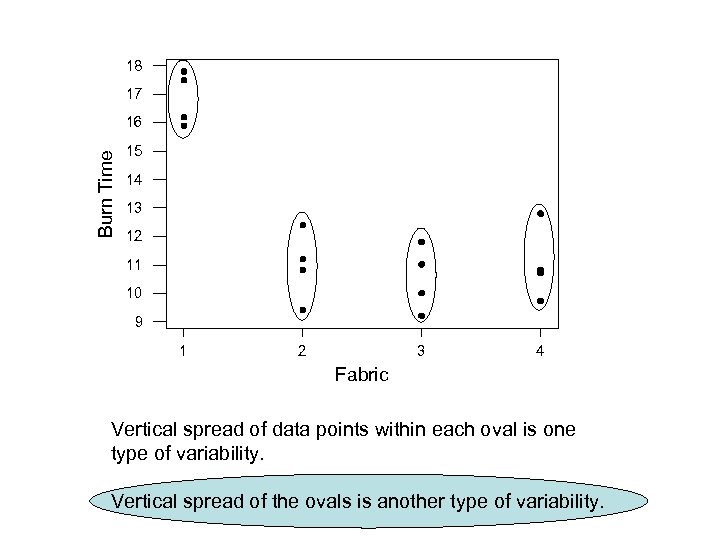 18 17 Burn Time 16 15 14 13 12 11 10 9 1 2 3 4 Fabric Vertical spread of data points within each oval is one type of variability. Vertical spread of the ovals is another type of variability.
18 17 Burn Time 16 15 14 13 12 11 10 9 1 2 3 4 Fabric Vertical spread of data points within each oval is one type of variability. Vertical spread of the ovals is another type of variability.
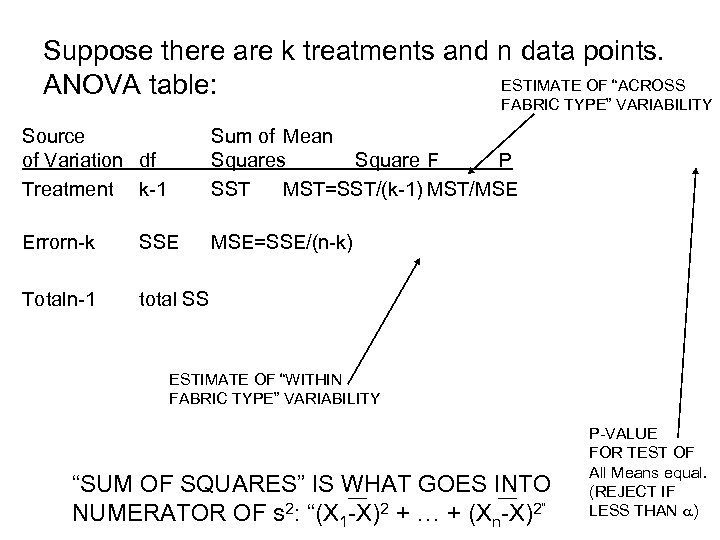 Suppose there are k treatments and n data points. ESTIMATE OF “ACROSS ANOVA table: FABRIC TYPE” VARIABILITY Source of Variation df Treatment k-1 Sum of Mean Squares Square F P SST MST=SST/(k-1) MST/MSE Errorn-k SSE MSE=SSE/(n-k) Totaln-1 total SS ESTIMATE OF “WITHIN FABRIC TYPE” VARIABILITY “SUM OF SQUARES” IS WHAT GOES INTO NUMERATOR OF s 2: “(X 1 -X)2 + … + (Xn-X)2” P-VALUE FOR TEST OF All Means equal. (REJECT IF LESS THAN a)
Suppose there are k treatments and n data points. ESTIMATE OF “ACROSS ANOVA table: FABRIC TYPE” VARIABILITY Source of Variation df Treatment k-1 Sum of Mean Squares Square F P SST MST=SST/(k-1) MST/MSE Errorn-k SSE MSE=SSE/(n-k) Totaln-1 total SS ESTIMATE OF “WITHIN FABRIC TYPE” VARIABILITY “SUM OF SQUARES” IS WHAT GOES INTO NUMERATOR OF s 2: “(X 1 -X)2 + … + (Xn-X)2” P-VALUE FOR TEST OF All Means equal. (REJECT IF LESS THAN a)
 One-way ANOVA: Burn Time versus Fabric Analysis of Variance for Burn Time Source DF SS MS F Fabric 3 109. 81 36. 60 27. 15 Error 12 16. 18 1. 35 Total 15 125. 99 P 0. 000 For test: H 0: m 1=m 2=m 3=m 4 Explaining why ANOVA is an analysis of variance: MST = 109. 81 / 3 = 36. 60 Sqrt(MST) describes standard deviation among the fabrics. MSE = 16. 18 / 12 = 1. 35 Sqrt(MSE) describes standard deviation of burn time within each fabric type. (MSE is estimate of variance of each burn time. ) F = MST / MSE = 27. 15 It makes sense that this is large and p-value = Pr(F 4 -1, 16 -4 > 27. 15) = 0 is small because the variance “among treatments” is much larger than variance within the units that get each treatment. (Note that the F test assumes the burn times are independent and normal with the same variance. )
One-way ANOVA: Burn Time versus Fabric Analysis of Variance for Burn Time Source DF SS MS F Fabric 3 109. 81 36. 60 27. 15 Error 12 16. 18 1. 35 Total 15 125. 99 P 0. 000 For test: H 0: m 1=m 2=m 3=m 4 Explaining why ANOVA is an analysis of variance: MST = 109. 81 / 3 = 36. 60 Sqrt(MST) describes standard deviation among the fabrics. MSE = 16. 18 / 12 = 1. 35 Sqrt(MSE) describes standard deviation of burn time within each fabric type. (MSE is estimate of variance of each burn time. ) F = MST / MSE = 27. 15 It makes sense that this is large and p-value = Pr(F 4 -1, 16 -4 > 27. 15) = 0 is small because the variance “among treatments” is much larger than variance within the units that get each treatment. (Note that the F test assumes the burn times are independent and normal with the same variance. )
 It turns out that ANOVA is a special case of regression. We’ll come back to that in a class or two. First, let’s learn about regression (chapters 12 and 13). • Simple Linear Regression example: Ingrid is a small business owner who wants to buy a fleet of Mitsubishi sigmas. To save $ she decides to buy second hand cars and wants to estimate how much to pay. In order to do this, she asks one of her employees to collect data on how much people have paid for these cars recently. (From Matt Wand)
It turns out that ANOVA is a special case of regression. We’ll come back to that in a class or two. First, let’s learn about regression (chapters 12 and 13). • Simple Linear Regression example: Ingrid is a small business owner who wants to buy a fleet of Mitsubishi sigmas. To save $ she decides to buy second hand cars and wants to estimate how much to pay. In order to do this, she asks one of her employees to collect data on how much people have paid for these cars recently. (From Matt Wand)
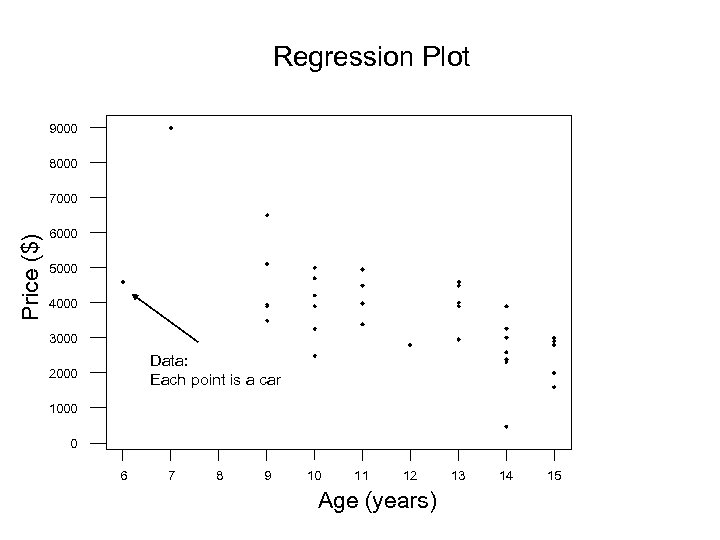 Regression Plot 9000 8000 Price ($) 7000 6000 5000 4000 3000 Data: Each point is a car 2000 1000 0 6 7 8 9 10 11 12 Age (years) 13 14 15
Regression Plot 9000 8000 Price ($) 7000 6000 5000 4000 3000 Data: Each point is a car 2000 1000 0 6 7 8 9 10 11 12 Age (years) 13 14 15
 • Plot suggests a simple model: Price of car = intercept + slope times car’s age + error or yi = b 0 + b 1 xi + ei, i = 1, …, 39. Estimate b 0 and b 1. Outline for Regression: 1. 2. 3. 4. Estimating the regression parameters and ANOVA tables for regression Testing and confidence intervals Multiple regression models & ANOVA Regression Diagnostics
• Plot suggests a simple model: Price of car = intercept + slope times car’s age + error or yi = b 0 + b 1 xi + ei, i = 1, …, 39. Estimate b 0 and b 1. Outline for Regression: 1. 2. 3. 4. Estimating the regression parameters and ANOVA tables for regression Testing and confidence intervals Multiple regression models & ANOVA Regression Diagnostics
 • Plot suggests a model: Price of car = intercept + slope times car’s age + error or yi = b 0 + b 1 xi + ei, i = 1, …, 39. Estimate b 0 and b 1 with b 0 and b 1. Find these with “least squares”. In other words, find b 0 and b 1 to minimize sum of squared errors: SSE = {y 1 – (b 0 + b 1 x 1)}2 + … + {yn – (b 0 + b 1 xn)}2 Each term is squared difference between observed y and the regression line ((b 0 + b 1 x 1) See green line on next page.
• Plot suggests a model: Price of car = intercept + slope times car’s age + error or yi = b 0 + b 1 xi + ei, i = 1, …, 39. Estimate b 0 and b 1 with b 0 and b 1. Find these with “least squares”. In other words, find b 0 and b 1 to minimize sum of squared errors: SSE = {y 1 – (b 0 + b 1 x 1)}2 + … + {yn – (b 0 + b 1 xn)}2 Each term is squared difference between observed y and the regression line ((b 0 + b 1 x 1) See green line on next page.
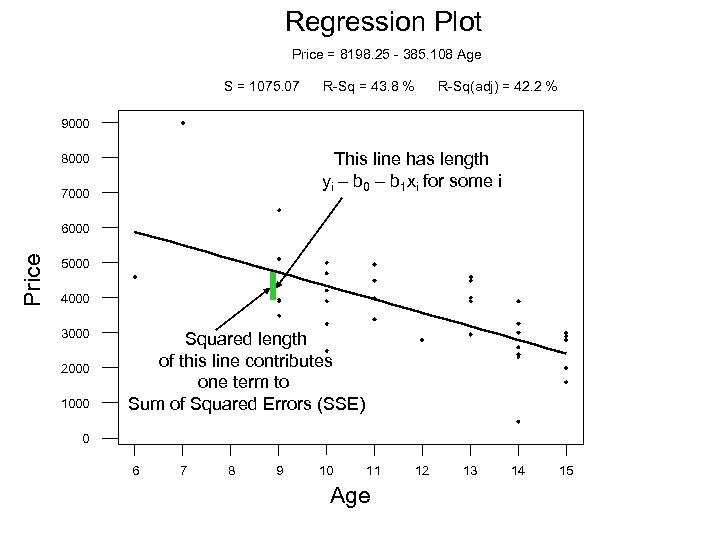 Regression Plot Price = 8198. 25 - 385. 108 Age S = 1075. 07 R-Sq = 43. 8 % R-Sq(adj) = 42. 2 % 9000 This line has length yi – b 0 – b 1 xi for some i 8000 7000 Price 6000 5000 4000 3000 2000 1000 Squared length of this line contributes one term to Sum of Squared Errors (SSE) 0 6 7 8 9 10 11 Age 12 13 14 15
Regression Plot Price = 8198. 25 - 385. 108 Age S = 1075. 07 R-Sq = 43. 8 % R-Sq(adj) = 42. 2 % 9000 This line has length yi – b 0 – b 1 xi for some i 8000 7000 Price 6000 5000 4000 3000 2000 1000 Squared length of this line contributes one term to Sum of Squared Errors (SSE) 0 6 7 8 9 10 11 Age 12 13 14 15
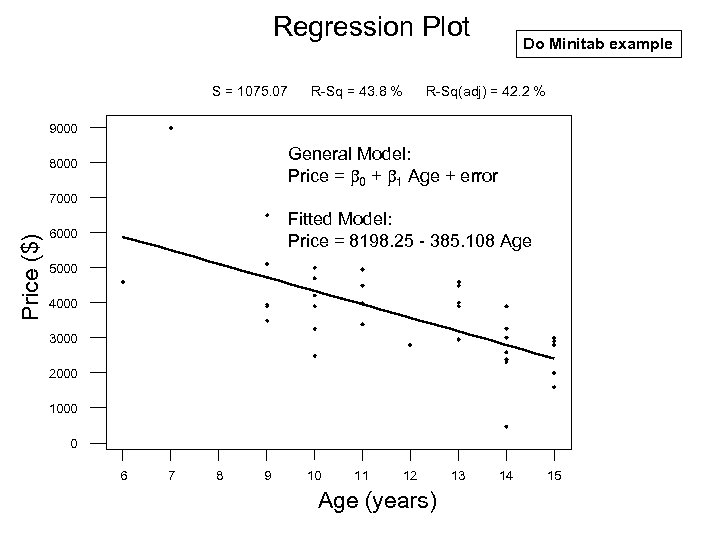 Regression Plot S = 1075. 07 R-Sq = 43. 8 % Do Minitab example R-Sq(adj) = 42. 2 % 9000 General Model: Price = b 0 + b 1 Age + error 8000 Price ($) 7000 Fitted Model: Price = 8198. 25 - 385. 108 Age 6000 5000 4000 3000 2000 1000 0 6 7 8 9 10 11 12 Age (years) 13 14 15
Regression Plot S = 1075. 07 R-Sq = 43. 8 % Do Minitab example R-Sq(adj) = 42. 2 % 9000 General Model: Price = b 0 + b 1 Age + error 8000 Price ($) 7000 Fitted Model: Price = 8198. 25 - 385. 108 Age 6000 5000 4000 3000 2000 1000 0 6 7 8 9 10 11 12 Age (years) 13 14 15
 Regression parameter estimates, b 0 and b 1, minimize SSE = {y 1 – (b 0 + b 1 x 1)}2 + … + {y – (b 0 + b 1 xn)}2 Full model is yi = b 0 + b 1 xi + ei Suppose errors (ei’s) are independent N(0, s 2). What do you think a good estimate of s 2 is? MSE = SSE/(n-2) is an estimate of s 2. Note how SSE looks like the numerator in s 2.
Regression parameter estimates, b 0 and b 1, minimize SSE = {y 1 – (b 0 + b 1 x 1)}2 + … + {y – (b 0 + b 1 xn)}2 Full model is yi = b 0 + b 1 xi + ei Suppose errors (ei’s) are independent N(0, s 2). What do you think a good estimate of s 2 is? MSE = SSE/(n-2) is an estimate of s 2. Note how SSE looks like the numerator in s 2.
 (I divided price by $1000. Think about why this doesn’t matter. ) Source Regression Residual Error Total DF 1 37 38 SS 33. 274 42. 763 76. 038 MS 33. 274 1. 156 F 28. 79 P 0. 000 Sum of Squares Total = {y 1 –mean(y)}2 + … + {y 39 – mean(y)}2 = 76. 038 Sum of Squared Errors = {y 1 – (b 0 + b 1 x 1)}2 + … + {y – (b 0 + b 1 xn)}2 = 42. 763 Sum of Squares for Regression = SSTotal - SSE What do these mean?
(I divided price by $1000. Think about why this doesn’t matter. ) Source Regression Residual Error Total DF 1 37 38 SS 33. 274 42. 763 76. 038 MS 33. 274 1. 156 F 28. 79 P 0. 000 Sum of Squares Total = {y 1 –mean(y)}2 + … + {y 39 – mean(y)}2 = 76. 038 Sum of Squared Errors = {y 1 – (b 0 + b 1 x 1)}2 + … + {y – (b 0 + b 1 xn)}2 = 42. 763 Sum of Squares for Regression = SSTotal - SSE What do these mean?
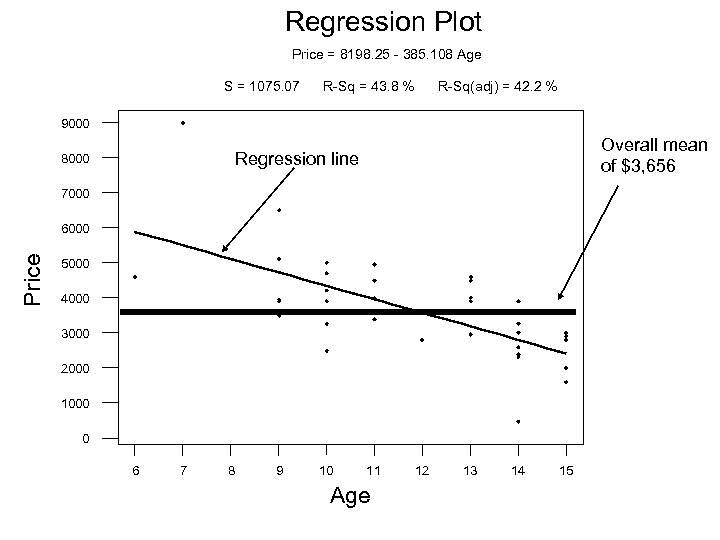 Regression Plot Price = 8198. 25 - 385. 108 Age S = 1075. 07 R-Sq = 43. 8 % R-Sq(adj) = 42. 2 % 9000 Overall mean of $3, 656 Regression line 8000 7000 Price 6000 5000 4000 3000 2000 1000 0 6 7 8 9 10 11 Age 12 13 14 15
Regression Plot Price = 8198. 25 - 385. 108 Age S = 1075. 07 R-Sq = 43. 8 % R-Sq(adj) = 42. 2 % 9000 Overall mean of $3, 656 Regression line 8000 7000 Price 6000 5000 4000 3000 2000 1000 0 6 7 8 9 10 11 Age 12 13 14 15
 (I divided price by $1000. Think about why this doesn’t really matter. ) Source Regression Residual Error Total DF 1=p-1 37=n-p 38=n-1 SS 33. 274 42. 763 76. 038 MS 33. 274 1. 156 F 28. 79 P 0. 000 p is the number of regression parameters (2 for now) SSTotal = {y 1 –mean(y)}2 + … + {y 39 – mean(y)}2 = 76. 038 SSTotal / 38 is an estimate of the variance around the overall mean. (i. e. variance in the data without doing regression) SSE = {y 1 – (b 0 + b 1 x 1)}2 + … + {y – (b 0 + b 1 xn)}2 = 42. 763 MSE = SSE / 37 is an estimate of the variance around the line. (i. e. variance that is not explained by the regression) SSR = SSTotal – SSE MSR = SSR / 1 is the variance the data that is “explained by the regression”.
(I divided price by $1000. Think about why this doesn’t really matter. ) Source Regression Residual Error Total DF 1=p-1 37=n-p 38=n-1 SS 33. 274 42. 763 76. 038 MS 33. 274 1. 156 F 28. 79 P 0. 000 p is the number of regression parameters (2 for now) SSTotal = {y 1 –mean(y)}2 + … + {y 39 – mean(y)}2 = 76. 038 SSTotal / 38 is an estimate of the variance around the overall mean. (i. e. variance in the data without doing regression) SSE = {y 1 – (b 0 + b 1 x 1)}2 + … + {y – (b 0 + b 1 xn)}2 = 42. 763 MSE = SSE / 37 is an estimate of the variance around the line. (i. e. variance that is not explained by the regression) SSR = SSTotal – SSE MSR = SSR / 1 is the variance the data that is “explained by the regression”.
 (I divided price by $1000. Think about why this doesn’t really matter. ) Source Regression Residual Error Total DF 1=p-1 37=n-p 38=n-1 SS 33. 274 42. 763 76. 038 MS 33. 274 1. 156 F 28. 79 P 0. 000 p is the number of regression parameters A test of H 0: b 1 = 0 versus HA: parameter is not 0 Reject if the variance explained by the regression is high compared to the unexplained variability in the data. Reject if F is large. F = MSR / MSE p-value is Pr(Fp-1, n-p > MSR / MSE) Reject H 0 for any a less than the p-value (Assuming errors are independent and normal. )
(I divided price by $1000. Think about why this doesn’t really matter. ) Source Regression Residual Error Total DF 1=p-1 37=n-p 38=n-1 SS 33. 274 42. 763 76. 038 MS 33. 274 1. 156 F 28. 79 P 0. 000 p is the number of regression parameters A test of H 0: b 1 = 0 versus HA: parameter is not 0 Reject if the variance explained by the regression is high compared to the unexplained variability in the data. Reject if F is large. F = MSR / MSE p-value is Pr(Fp-1, n-p > MSR / MSE) Reject H 0 for any a less than the p-value (Assuming errors are independent and normal. )
 R 2 • Another summary of a regression is: R 2 = Sum of Squares for Regression Sum of Squares Total 0<= R 2 <= 1 This is the percentage of the of variation in the data that is described by the regression.
R 2 • Another summary of a regression is: R 2 = Sum of Squares for Regression Sum of Squares Total 0<= R 2 <= 1 This is the percentage of the of variation in the data that is described by the regression.
 Two different ways to assess “worth” of a regression 1. Absolute size of slope: bigger = better 2. Size of error variance: smaller = better 1. R 2 close to one 2. Large F statistic
Two different ways to assess “worth” of a regression 1. Absolute size of slope: bigger = better 2. Size of error variance: smaller = better 1. R 2 close to one 2. Large F statistic
