Angles and Arcs Section 10 -2 central

Angles and Arcs Section 10 -2

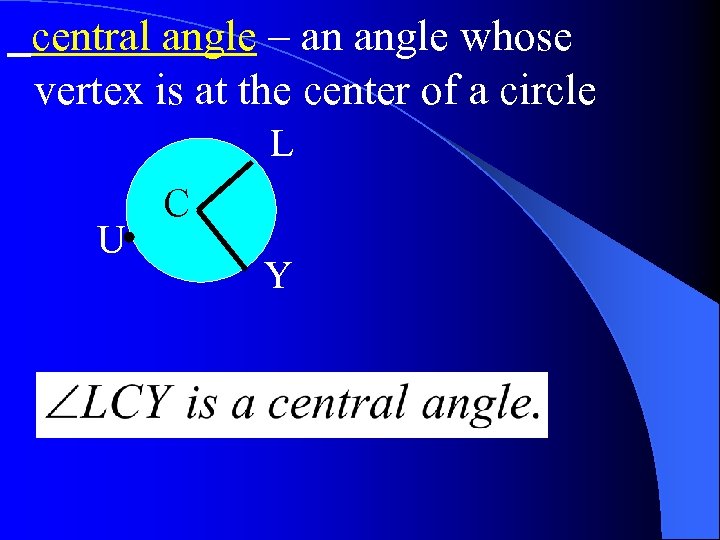central angle – an angle whose vertex is at the center of a circle L U C Y

Theorem 10 -1 l. In the same or in congruent circles, two arcs are congruent iff their corresponding central angles are congruent.

Sum of Central Angles The sum of the measures of the central angles of a circle with no interior points in common is 360 o.

LUY is a major arc L U C LY is a minor arc Y A minor arc consists of its endpoints and all points on the circle interior to the angle. A major arc uses 3 letters to name the arc and consists of its endpoints and all points on the circle exterior to the angle.

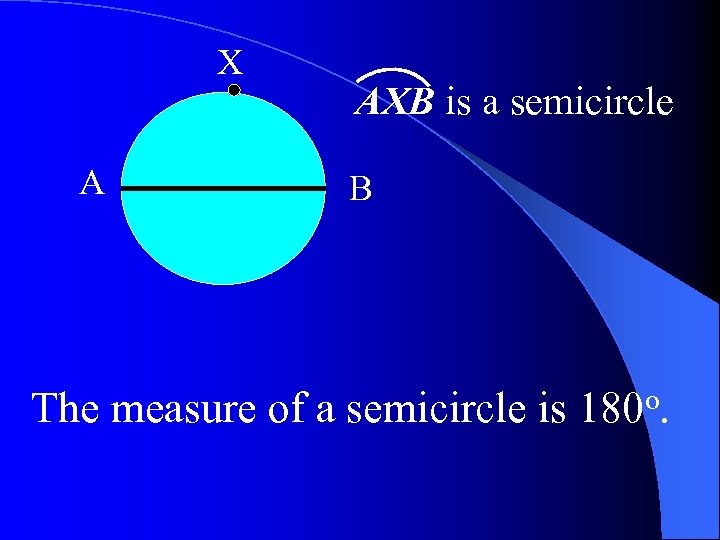X A AXB is a semicircle B The measure of a semicircle is 180 o.

Definition of Arc Measure The measure of a minor arc is the measure of its central angle. The measure of a major arc is 360 minus the measure of its central angle. P 100 o C R m PM = 100 o M m PRM = 260 o

Arc Addition Postulate The measure of an arc formed by 2 adjacent arcs is the sum of the measures of the 2 arcs. That is, if Q is a point on PR, then P m PQ + m QR = m PQR. Q R

Arc Length The arc length is different from the degree measure of an arc. Suppose a circle was made of string. The length of the arc would be the linear distance of that piece of string representing the arc.

Arc Length =

Concentric circles lie in the same plane and have the same center, but have different radii. All circles are similar, so concentric circles are also similar.

Joke Time What flower grows between your nose and your chin? Tulips

Why were Goldilocks and the Big Bad Wolf in the same house? It was two-story