Математика на английском.pptx
- Количество слайдов: 41
Analysis Sets The individual objects of the set are called members or elements. Any part of a set is called a subset of the given set. The set consisting of no elements is called the empty set or null set. Отдельные объекты множества называются членами или элементами. Любая часть множества называется подмножеством данного множества. Множество, не содержащее элементов, называется пустым множеством. object member element subset given empty null объект член элемент подмножество данный пустой нуль 1

Real Numbers The number system based on the symbols 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 is called a base ten system. Система счисления, основанная на символах, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 называется десятичной системой счисления. real symbol base действительный символ основание 2

Natural numbers 1. Natural numbers 1, 2, 3, 4, . . . , also called positive integers, are used in counting members of a set. The sum a + b and product a・b or ab of any two natural numbers a and b is also a natural number. The set of natural numbers is closed under the operations of addition and multiplication, or satisfies the closure property with respect to these operations. 1. Натуральные числа 1, 2, 3, 4, . . . , называемые также положительными целыми, используются при подсчете членов множества. Сумма а + b и произведение а · b или аb любых двух натуральных чисел а и b также натуральное число. Множество натуральных чисел замкнуто относительно операций сложения и умножения, или удовлетворяет свойству замкнутости относительно этих операций. natural positive integer count operation closure property with respect to натуральный положительный целый считать операция замкнутый свойство по отношению к 3

Integer numbers 2. Negative integers and zero, denoted by – 1, – 2, – 3, . . . , and 0, respectively, arose to permit solutions of equations such as x + b = a, where a and b are any natural numbers. This leads to the operation of subtraction, or inverse of addition, and we write x = a – b. The set of positive and negative integers and zero is called the set of integers. 2. Отрицательные числа и ноль, обозначаемые -1, -2, -3, . . . , , и 0, соответственно, возникли для обеспечения решения уравнений, таких как x + b = a, где а и b – любые натуральные числа. Это приводит к операции вычитания или обращению сложения, и мы пишем x = a – b. Множество положительных и отрицательных чисел и нуля, называется множеством целых чисел. . negative arise permit lead subtraction отрицательный возникать позволять вести вычитание 4

Rational numbers 3. Rational numbers or fractions such as 2/3 , 5/4, . . . arose to permit solutions of equations such as bx = a for all integers a and b, where b _ 0. This leads to the operation of division, or inverse of multiplication, and we write x = a/b or a ÷ b, where a is the numerator and b the denominator. The set of integers is a subset of the rational numbers, since integers correspond to rational numbers where b = 1. 3. Рациональные числа или дроби, такие как 2/3 , 5/4, . . . , возникли, чтобы позволить решения уравнений, таких как bx = a для всех целых чисел а и b, где b _ 0. Это приводит к операции деления, или обращения умножения, и мы пишем x = a/b или a ÷ b, где a, где а – числитель и b – знаменатель. Множество целых чисел есть подмножество рациональных чисел, так как целые числа соответствуют рациональным числам, в которых b = 1. . rational fractions division numerator denominator рациональный дробь деление числитель знаменатель 5

Irrational numbers 4. Irrational numbers such as and π are numbers which are not rational; i. e. , they cannot be expressed as a/b (called the quotient of a and b), where a and b are integers and b 0. The set of rational and irrational numbers is called the set of real numbers. 4. Иррациональные числа, такие как и π – числа, которые не являются рациональными; т. е. они не могут быть выражены в виде a/ b (называемому частным а и b), где а и b целые и b 0. Множество рациональных и иррациональных чисел называется множеством действительных чисел . irrational иррациональный express выражать quotient частное 6
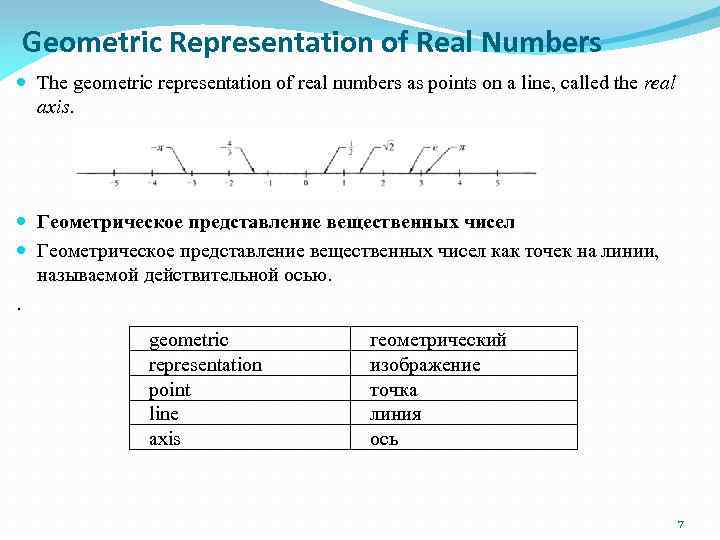
Geometric Representation of Real Numbers The geometric representation of real numbers as points on a line, called the real axis. Геометрическое представление вещественных чисел как точек на линии, называемой действительной осью. . geometric representation point line axis геометрический изображение точка линия ось 7
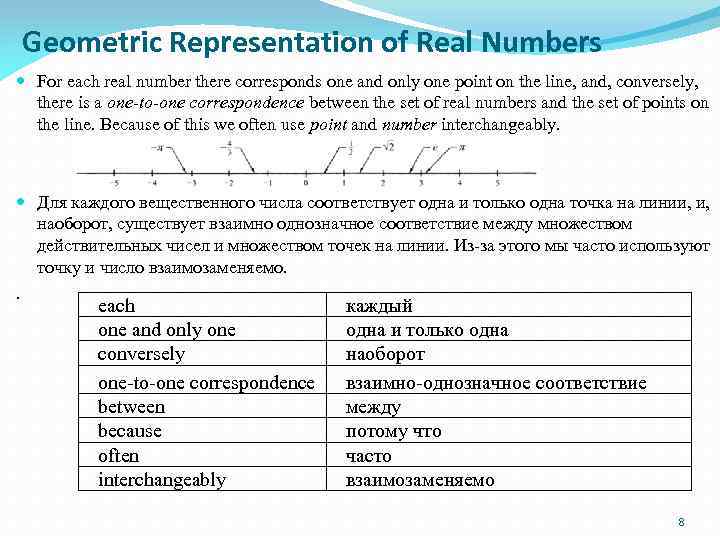
Geometric Representation of Real Numbers For each real number there corresponds one and only one point on the line, and, conversely, there is a one-to-one correspondence between the set of real numbers and the set of points on the line. Because of this we often use point and number interchangeably. Для каждого вещественного числа соответствует одна и только одна точка на линии, и, наоборот, существует взаимно однозначное соответствие между множеством действительных чисел и множеством точек на линии. Из-за этого мы часто используют точку и число взаимозаменяемо. . each one and only one conversely one-to-one correspondence between because often interchangeably каждый одна и только одна наоборот взаимно-однозначное соответствие между потому что часто взаимозаменяемо 8

Geometric Representation of Real Numbers The set of real numbers to the right of 0 is called the set of positive numbers, the set to the left of 0 is the set of negative numbers, while 0 itself is neither positive nor negative. Множество действительных чисел справа от 0 называется множеством положительных чисел, множество слева от 0 – множеством отрицательных чисел, в то время как 0 само по себе не является ни положительным, ни отрицательным. to the right of … справа от … to the left of … слева от … neither … nor ни … ни… 9

Operations with Real Numbers If a, b, c belong to the set R of real numbers, then: . Если a, b, c принадлежат множеству R of действительных чисел, тогда: 1 a + b and ab belong to R Closure law Закон замыкания 2 . a + b = b + a Commutative law of addition Коммутативный закон для сложения 3 a + (b + c) = (a + b) + c Associative law of addition Ассоциативный закон для сложения 4 ab = ba 5 a(bc) = (ab)c 6 a(b + c) = ab + ac 7 a + 0 = 0 + a = a, 1・a = a・ 1 = a Commutative law of multiplication Associative law of multiplication belong closure commutative law associative distributive Distributive law Коммутативный закон для умножения Ассоциативный закон для умножения Дистрибутивный закон принадлежать замыкание коммутативнный закон ассоциативный дистрибутивный 10

Inequalities If a – b is a nonnegative number, we say that a is greater than or equal to b or b is less than or equal to a, and write, respectively, a > b or b < a. If there is no possibility that a = b, we write a > b or b < a. Geometrically, a > b if the point on the real axis corresponding to a lies to the right of the point corresponding to b. Неравенства Если a – b неотрицательное число, мы говорим, что a больше или равно b или b is меньше или равно a, и пишем, соответственно, a > b или b < a. Если невозможно, что a = b, мы пишем a > b или b < a. Геометрически, a > b если точка на действительной оси, соответствующая a лежит справа от точки, соответствующей b. inequality nonnegative greater than or equal less than or equal lie неравенство неотрицательный большой больше или равно меньше или равно лежать 11

Absolute Value of Real Numbers The absolute value of a real number a, denoted by |a|, is defined as a if a > 0, – a if a < 0, and 0 if a = 0. The distance between any two points (real numbers) a and b on the real axis is |a–b| = |b–a|. Абсолютное значение действительных чисел Абсолютное значение действительного числа a, обозначаемое |a|, определяется как a если a > 0, – a если a < 0, и 0 если a = 0. Расстояние между двумя точками (действительными числами) a и b на действительной оси есть |a–b| = |b–a|. absolute distance абсолютный расстояние 12

Exponents and Roots The product a・ a. . . a of a real number a by itself p times is denoted by ap, where p is called the exponent and a is called the base. If ap = N, where p is a positive integer, we call a a pth root of N, written If p and q are positive integers, we define . Показатели и корни Произведение a・ a. . . a действительного числа a на себя p обозначают ap, где p называют показателем и a называют основанием. Если ap = N, где p положительное число, мы называем a a p-ым корнем из N, пишется Если p и q положительные целые, мы определяем . exponent root itself base показатель корень себя основание 13

Logarithms If ap = N, p is called the logarithm of N to the base a, written p = loga N. If a and N are positive and a 1, there is only one real value for p. Логарифмы Если ap = N, p называют логарифмом N по основанию a, пишется p = loga N. Если a и N положительны и a 1, существует только одно действительное значение для p. . logarithm логарифм 14

Logarithms In practice, two bases are used: base a = 10, and the natural base a = e = 2. 71828. . The logarithmic systems associated with these bases are called common and natural, respectively. The common logarithm system is signified by log N; i. e. , the subscript 10 is not used. For natural logarithms, the usual notation is ln N. На практике два основания применяют: основание a = 10, и натуральное основание a = e = 2, 71828. . Логарифмические системы, связанные с этими основаниями, называют обыкновенной и натуральной, соответственно. Десятичная логарифмическая система обозначается signified log N; то есть, нижний индекс 10 не используется. Для натуральных логарифмов обычная запись – ln N. . common общий common logarithm signify natural logarithm use usual notation десятичный логарифм обозначать натуральный логарифм использовать обычный запись 15

Intervals The set of points x such that a x b is called a closed interval and is denoted by [a, b]. The set a < x < b is called an open interval, denoted by (a, b). The sets a < x b and a x < b, denoted by (a, b] and [a, b), respectively, are called half-open or half-closed intervals. Множество точек x, таких, что a x b называется a закрытым интервалом и обозначается [a, b]. Множество a < x < b называется открытым интервалом, обозначаемым (a, b). Множества a < x b и a x < b, обозначаемые (a, b] и [a, b), соответственно, называются полу or half-closed intervals. . interval closed interval open interval half-open half-closed интервал замкнутый интервал открытый интервал полуоткрытый полузакрытый 16

Intervals The set x > a can also be represented by a < x < _. Such a set is called an infinite or unbounded interval. Similarly, –_ < x < represents all real numbers x. Множество x > a может также быть представлено как a < x < _. Такое множество называется an бесклнечным или неограниченным интервалом. Аналогично, –_ < x < _ представляет все действительные числа. . infinite nterval unbounded nterval бесконечный интервал неограниченный интервал 17

Neighborhoods The set of all points x such that |x – a|< δ, where δ > 0, is called a δ neighborhood of the point a. The set of all points x such that 0 < |x – a| < δ, in which x = a is excluded, is called a deleted δ neighborhood of a or an open ball of radius δ about a. Множество всех точек x таких, что |x – a|< δ, где δ > 0, называется δ окрестностью точки a. Множество всех точек x, таких что 0 < |x – a| < δ, в котором x = a исключено, называетсяa проколотой δ окрестностью a или открытым шаром радиуса δ около a. . neighborhood deleted δ neighborhood ball radius about окрестность проколотая δ окрестность шар радиус около 18

Bounds If for all numbers x of a set there is a number M such that x < M, the set is bounded above and M is called an upper bound. Similarly if x > m, the set is bounded below and m is called a lower bound. If for all x we have m < x < M, the set is called bounded. Если для всех чисел x множества существует число M такое что x < M, множество ограничено сверху и M называется верхней границей. Аналогично, если x > m, множество ограничено снизу и m называется a нижней границей. Если для всех x мы имеем m < x < M, множество называется ограниченным. bounded above upper bounded below lower bounded ограниченный сверху верхняя граница ограниченный снизу нижняя граница ограниченный 19

Algebraic and Transcendental Numbers A number x which is a solution to the polynomial equation a 0 xn + a 1 xn– 1 + a 2 xn– 2 +. . . + an– 1 x + an = 0 where a 0 0, a 1, a 2, . . . , an are integers and n is a positive integer, called the degree of polynomial, is called an algebraic number. A number which cannot be expressed as a solution of any polynomial equation with integer coefficients is called a transcendental number. Число x которое является решением степенного уравнения (…) где a 0 0, a 1, a 2, . . . , an целые и n положительное целое, называемое степенью многочлена, называется алгебраическим числом. Числа, которые не могут быть выражены как решение какого-нибудь степенного уравнения с целыми коэффициентами, называются трансцедентными числами. . polynom degree algebraic number transcendental number многочлен степень алгебраичечкое число трансцендентное число 20

The Complex Number System We can consider a complex number as an object having the form a + bi, where a and b are real numbers called the real and imaginary parts, and i = is called the imaginary unit. Мы рассматриваем комплексное число как объект, имеющий форму a + bi, где a и b действительные числа, называемые действительной и мнимой частями, и i = называется мнимой единицей. . complex number real part imaginary unit комплексное число действительная часть мнимая единица 21

The Complex Number System The absolute value or modulus of a + bi is defined as |a + bi| = . The complex conjugate of a + bi is defined as a – bi. The complex conjugate of the complex number z is often indicated by or z*. Абсолютное значение или модуль a + bi определяется как |a + bi| = . Комплексно сопряженное к a + bi определяется как a – bi. Комплексно сопряженное комплексного числа z часто обозначается как or z*. absolute value modulus conjugate complex conjugate абсолютная величина модуль сопряженный комплексно сопряженный 22

Polar Form of Complex Numbers Since a complex number x + iy can be considered as an ordered pair (x, y), we can represent such numbers by points in an xy plane called the complex plane. Так комплексное число x + iy может рассматриваться как упорядоченная пара (x, y), мы можем представить эти числа точками на xy плоскости, называемой комплексной плоскостью. polar ordered pair plane complex plane полярный упорядоченная пара плоскость комплексная плоскость 23

Polar Form of Complex Numbers We see that x = ρ cos φ, y = ρ sin φ, where =| x + iy| and φ, called the amplitude and argument, is the angle which line OP makes with the positive x axis OX. It follows that z = x + iy = ρ(cos φ + i sin φ) called the polar form of the complex number, where ρ and φ are called polar coordinates. It is sometimes convenient to write cis φ instead of cos φ + i sin φ. Мы видим, что x = ρ cos φ, y = ρ sin φ, где = |x + iy| и φ, называемые амплитудой и аргументом, – угол, который линия OP делает с положительным x оси. OX. Отсюда следует, что z = x + iy = ρ(cos φ + i sin φ), называемое полярной формой комплексного числа, где ρ и φ называются полярными координатами. Иногда удобно писать cis φ вместо cos φ + i sin φ. amplitude амплитуда argument аргумент angle угол polar form полярная форма polar coordinates полярные координаты convenient удобный 24

Polar Form of Complex Numbers If z 1 = x 1 + iy 1 = ρ1 (cos φ1 + i sin φ1) and z 2 = x 2 + iy 2 = ρ2(cosφ2 + i sin φ2) and by using the addition formulas for sine and cosine, we can show that z 1 z 2 = ρ1ρ2{cos(φ1 + φ2) + i sin(φ1 + φ2)} Если z 1 = x 1 + iy 1 = ρ1 (cos φ1 + i sin φ1) и z 2 = x 2 + iy 2 = ρ2(cosφ2 + i sin φ2), используя формулу сложения для синуса и косинуса, мы можем показать, что (…) sine cosine синус косинус 25

Function A function is composed of a domain set, a range set, and a rule of correspondence that assigns exactly one element of the range to each element of the domain. Функция состоит из области определения, области значений и правила соответствия, которое назначает точно один элемент из области значений каждому элементу из области определения. domain set range set rule область определения область значений правило 26

Monotonic Functions A function is called monotonic increasing in an interval if for any two points x 1 and x 2 in the interval, (x 1 < x 2), . If whenever x 1 < x 2, then f(x) the function is called strictly increasing. Функция называется монотонно неубывающей на интервале, если для любых двух точек x 1 и x 2 на интервале, ( x 1 < x 2), . Если функция называется монотонно возрастающей. monotonic increasing strictly increasing монотонно неубывающая монотонно возрастающая 27

Monotonic Functions A function is called monotonic decreasing in an interval if for any two points x 1 and x 2 in the interval, (x 1 < x 2), If whenever x 1 < x 2, then f(x) the function is called strictly вуcreasing. Функция называется монотонно невозрастающей на интервале, если для любых двух точек x 1 и x 2 на интервале, ( x 1 < x 2), . Если функция называется монотонно возрастающей. monotonic decreasing strictly decreasing монотонно невозрастающая монотонно убывающая 28

Inverse function Let the correspondence y=f(x) between the domain and range values be one-to-one. Then a new function f – 1, called the inverse function of f, can be created by interchanging the domain and range of f. This information is contained in the form x = f – 1(y). Пусть соответствие y=f(x) между областью определения и областью значений взаимно-однозначно. Тогда новая функция f – 1, называемая обратной функцией f, может быть образована взаимозаменой областью определения и области значений f. Эта информация содержится в форме x = f – 1(y). inverse function обратная функция 29

Maximum and minimum If there exists an open interval (a, b) containing c such that f (x) < f (c) for all x other than c in the interval, then f (c) is a relative maximum of f. If f (x) > f (c) for all x in (a, b) other than c, then f (c) is a relative minimum of f. Если существует открытый интервал (a, b) содержащий c такой, что f (x) < f (c) для всех x ероме c в этом интервале, тогда f (c) – локальный максимум f. Если f (x) > f (c) для всех x in (a, b) кроме c, тогда f (c) – локальный минимум f. relative maximum relative minimum локальный максимум локальный минимум 30

Types of Elementary Functions 1. Polynomial functions have the form where a 0, . . . , an are constants and n is a positive integer called the degree of the polynomial if 2. Algebraic functions are functions satisfying an equation of the form where are polynomials in x. If the function can be expressed as the quotient of two polynomials, i. e. , where P(x) and Q(x) are polynomials, it is called a rational algebraic function; otherwise, it is an irrational algebraic function. 31

Types of Elementary Functions 3. Transcendental functions are functions which are not algebraic; i. e. , they do not satisfy equations of the form of previous Equation. 3. 1. Exponential function: 3. 2. Logarithmic function: . If a = e = 2. 71828. . . , called the natural base of logarith we write , called the natural logarithm of x. 32

Types of Elementary Functions 3. 3. Trigonometric functions (also called circular functions because of their geometric interpretation with respect to the unit circle): tangent cotangent secant cosecant тангенс котангенс секанс косеканс 33

Types of Elementary Functions 3. 4. Inverse trigonometric functions. The following is a list of the inverse trigonometric functions and their principal values: arc sine, anti-sine, inverse sine arc cosine, anti-sine , inverse cosine arc tangent, inverse tangent, anti-tangent arc cotangent, inverse cotangent, anti-cotangent арксинус арккосинус арктангенс арккотангенс 34

Types of Elementary Functions 3. 5. Hyperbolic functions. Hyperbolic гиперболический 35

Limit of Functions Let f (x) be defined and single-valued for all values of x near x = x 0 with the possible exception of x = x 0 itself (i. e. , in a deleted δ neighborhood of x 0). We say that the number l is the limit of f(x) as x approaches x 0 and write if for any positive number (however small) we can find some positive number δ (usually depending on ) such that whenever . In such a case we also say that f(x) approaches l as x approaches x 0 and write f (x) → l as x → x 0. Пусть f (x) определена и однозначна для всех значений x около x = x 0 с возможным исключением x = x 0 самой (т. е. , в проколотой δ окрестности x 0). Мы говорим, что число l –это предел f(x), когда x стремится к x 0 и пишем если для любого положительного числа (как угодно малого) мы можем найти такое положительное число δ (обычно зависящего от ) такое, что когда . . В этом случае, мы также говорим, что f(x) стремится к l при x стремящимся к x 0 и пишем f (x) → l as x → x 0. 36

Derivatives The derivative of the function f at its domain value x 0 is a limit If this limit can be formed at each point of a subdomain of the domain of f, then f is said to be differentiable on that subdomain and a new function f′ has been constructed. Производная функции f в точке ее области определения x 0 это предел …. . Если этот предел может быть образован в каждой точке подмножества области определения f, тогда f , говорят, дифференцируема на этом подмножестве и новая функция f′ построена. derivative производная subdomain подобласть differentiable дифференцируемый construct строить 37

Derivatives Let P 0 (x 0) be a point on the graph of y = f (x). Let P(x) be a nearby point on this same graph of the function f. Then the straight line through these two points is called a secant line. Its slope, ms, is the difference quotient where Δx and Δy are called the increments in x and y, respectively, h =x x 0=Δx. Пусть P 0 (x 0) - точка на графике y = f (x). Пусть P(x) является близкой точкой на том же графике функции f. Тогда прямая линия через эти две точки называется секущей. Ее наклон, ms, это разностное отношение где Δx и Δy называются приращениями x и y, соответственно, h =x– x 0=Δx. nearby straight secant slope difference quotient increment близкий прямая секущая наклон разностное отношение приращение 38

Differentials Let Δx = dx be an increment given to x. Then Δy = f (x + Δx) – f (x) is called the increment in y = f (x). If f (x) is continuous and has a continuous first derivative in an interval, then Δy = f ′(x) Δx + Δx where → 0 as Δx → 0. The expression dy = f ′(x)dx is called the differential of y or f (x) or the principal part of Δy. Пусть Δx = dx приращение, данное x. Тогда Δy = f (x + Δx) – f (x) называется приращением y = f (x). если f (x) непрерывна и имеет непрерывную первую производную на интервале, тогда Δy = f ′(x) Δx + Δx где _ → 0 при Δx → 0. Выражение dy = f ′(x)dx называется дифференциалом y или f (x) или главной частью Δy. differential continuous expression principal part дифференциал непрерывный выражение главная часть 39

The Differentiation of Composite Functions If u=f(x) and y = g(u), respectively, then y =g(f(x)). The rule of composite function differentiation is called the chain rule and is represented by . IЕсли u=f(x) и y = g(u), соответственно, тогда y =g(f(x)) Правило дифференцирования сложных функций называется цепным правилом и представлено как…. differentiation composite functions chain rule дифференцирование сложная функция цепное правило 40

Higher-Order Derivatives If f (x) is differentiable in an interval, its derivative is given by f ′(x), y′ or dy/dx, where y = f (x). If f ′(x) is also differentiable in the interval, its derivative is denoted by f ″(x), y″ or . Similarly, the nth derivative of f (x), if it exists, is denoted by where n is called the order of the derivative. IЕсли f (x) is дифференцируема в интервалеl, ее производная, дается как f ′(x), y′ or dy/dx, где y = f (x). Если f ′(x) также дифференцируема на интервале, ее производная обозначается f ″(x), y″ or … Аналогично, n-ая производная f (x), если она существует, обозначается как …. где n is называется порядком производной. higher-order derivatives производные высших порядков 41
Математика на английском.pptx