Analysis Design of Algorithms CSCE 321 Prof

Analysis & Design of Algorithms (CSCE 321) Prof. Amr Goneid Department of Computer Science, AUC Part 10. Dynamic Programming Prof. Amr Goneid, AUC 1

Dynamic Programming Prof. Amr Goneid, AUC 2

Dynamic Programming n Introduction n What is Dynamic Programming? n How To Devise a Dynamic Programming n n n n Approach The Sum of Subset Problem The Knapsack Problem Minimum Cost Path Coin Change Problem Optimal BST DP Algorithms in Graph Problems Comparison with Greedy and D&Q Methods Prof. Amr Goneid, AUC 3

1. Introduction We have demonstrated that n Sometimes, the divide and conquer approach seems appropriate but fails to produce an efficient algorithm. n. One of the reasons is that D&Q produces overlapping subproblems. Prof. Amr Goneid, AUC 4

Introduction n Solution: Buy speed using space n Store previous instances to compute current instance n instead of dividing the large problem into two (or more) smaller problems and solving those problems (as we did in the divide and conquer approach), we start with the simplest possible problems. n We solve them (usually trivially) and save these results. These results are then used to solve slightly larger problems which are, in turn, saved and used to solve larger problems again. n This method is called Dynamic Programming n Prof. Amr Goneid, AUC 5

2. What is Dynamic Programming n An algorithm design method used when the solution is a result of a sequence of decisions (e. g. Knapsack, Optimal Search Trees, Shortest Path, . . etc). n Makes decisions one at a time. Never make an erroneous decision. n Solves a sub-problem by making use of previously stored solutions for all other subproblems. Prof. Amr Goneid, AUC 6

Dynamic Programming n Invented by American mathematician Richard Bellman in the 1950 s to solve optimization problems n“Programming” here means “planning” Prof. Amr Goneid, AUC 7

When is Dynamic Programming Two main properties of a problem that suggest that the given problem can be solved using Dynamic programming. n Overlapping Subproblems n Optimal Substructure Prof. Amr Goneid, AUC 8

Overlapping Subproblems n. Like Divide and Conquer, Dynamic Programming combines solutions to subproblems. Dynamic Programming is mainly used when solutions of same subproblems are needed again and again. n Examples are computing the Fibonacci Sequence, Binomial Coefficients, etc. Prof. Amr Goneid, AUC 9

Optimal Substructure: Principle of Optimality n Dynamic programming uses the Principle of Optimality to avoid non-optimal decision sequences. n For an optimal sequence of decisions, the remaining decisions must constitute an optimal sequence. n Example: Shortest Path Find Shortest path from vertex (i) to vertex (j) Prof. Amr Goneid, AUC 10

Principle of Optimality Let k be an intermediate vertex on a shortest ito-j path i , a , b, … , k , l , m , … , j. The path i , a , b, … , k must be shortest i-to-k , and the path k , l , m , … , j must be shortest k-to-j k i j l a b m Prof. Amr Goneid, AUC 11

3. How To Devise a Dynamic Programming Approach n Given a problem that is solvable by a Divide & n n n Conquer method Prepare a table to store results of sub-problems Replace base case by filling the start of the table Replace recursive calls by table lookups Devise for-loops to fill the table with sub-problem solutions instead of returning values Solution is at the end of the table Notice that previous table locations also contain valid (optimal) sub-problem solutions Prof. Amr Goneid, AUC 12

Example(1): Fibonacci Sequence n The Fibonacci graph is not a tree, indicating an Overlapping Subproblem. n Optimal Substructue: If F(n-2) and F(n-1) are optimal, then F(n) = F(n-2) + F(n-1) is optimal Prof. Amr Goneid, AUC 13

Fibonacci Sequence Dynamic Programming Solution: n Buy speed with space, a table F(n) n Store previous instances to compute current instance Prof. Amr Goneid, AUC 14

Fibonacci Sequence Fib(n): Table F[n] if (n < 2) return 1; F[0] = F[1] = 1; else if ( n >= 2) return Fib(n-1) + Fib(n-2) for i = 2 to n F[i] = F[i-1] + F[i-2]; i-2 i-1 i return F[n]; Prof. Amr Goneid, AUC 15

Fibonacci Sequence Dynamic Programming Solution: n Space Complexity is O(n) n Time Complexity is T(n) = O(n) Prof. Amr Goneid, AUC 16

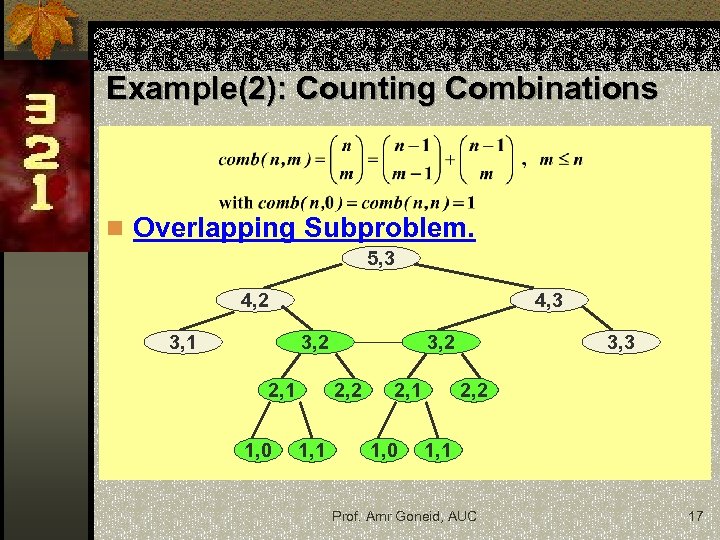Example(2): Counting Combinations n Overlapping Subproblem. 5, 3 4, 2 3, 1 4, 3 3, 2 2, 1 1, 0 3, 2 2, 2 1, 1 2, 1 1, 0 3, 3 2, 2 1, 1 Prof. Amr Goneid, AUC 17

Counting Combinations n Optimal Substructure The value of Comb(n, m) can be recursively calculated using following standard formula for Binomial Coefficients: Comb(n, m) = Comb(n-1, m-1) + Comb(n-1, m) Comb(n, 0) = Comb(n, n) = 1 Prof. Amr Goneid, AUC 18

Counting Combinations Dynamic Programming Solution: n Buy speed with space, Pascal’s Triangle. Use a table T[0. . n, 0. . m]. n Store previous instances to compute current instance Prof. Amr Goneid, AUC 19

Counting Combinations comb(n, m): if ((m == 0) || (m == n)) return 1; else return comb (n − 1, m − 1) + comb (n − 1, m); i-1, j-1 i-1 , j Table T[n, m] for (i = 0 to n − m) T[i, 0] = 1; for (i = 0 to m) T[i, i] = 1; for (j = 1 to m) for (i = j + 1 to n − m + j) T[i, j] = T[i − 1, j − 1] + T[i − 1, j]; return T[n, m]; i, j Prof. Amr Goneid, AUC 20

Counting Combinations Example n=4, m=2 1 1 2 1 3 3 6 Prof. Amr Goneid, AUC 21

Counting Combinations Dynamic Programming Solution: n Space Complexity is O(nm) n Time Complexity is T(n) = O(nm) Prof. Amr Goneid, AUC 22

Exercise Consider the following function: Consider the number of arithmetic operations used to be T(n): n Show that a direct recursive algorithm would give an exponential complexity. n Explain how, by not re-computing the same F(i) value twice, one can obtain an algorithm with T(n) = O(n 2) n Give an algorithm for this problem that only uses O(n) arithmetic operations. Prof. Amr Goneid, AUC 23

4. The Sum of Subset Problem n Given a set of positive integers W = {w 1, w 2. . . wn} n The problem: is there a subset of W that sums exactly to m? i. e, is Sum. Sub (w, n, m) true? w 1 w 2 . . wn m n Example: W = { 11 , 13 , 27 , 7} , m = 31 A possible subset that sums exactly to 31 is {11 , 13 , 7} Hence, Sum. Sub (w, 4, 31) is true Prof. Amr Goneid, AUC 24

The Sum of Subset Problem n Consider the partial problem Sum. Sub (w, i, j) to return true if there is a subset of the first i items that sums up exactly to j: w 1 w 2 . . wi j n Sum. Sub (w, i, j) is true if: wi is not needed, and {w 1, . . , wi-1} has a subset that sums to (j), i. e. , Sum. Sub (w, i-1, j) is true, OR n wi is needed to fill the rest of (j), i. e. , {w 1, . . , wi-1} has a subset that sums to (j-wi) so that adding wi sums up exactly to j- wi + wi = j n If there are no elements, i. e. (i = 0) then Sum. Sub (w, 0, j) is true if (j = 0) and false otherwise n Prof. Amr Goneid, AUC 25

Divide & Conquer Approach Algorithm: bool Sum. Sub (w, i, j) { if (i == 0) return (j == 0); else if (Sum. Sub (w, i-1, j)) return true; else if ((j - wi) >= 0) return Sum. Sub (w, i-1, j - wi); else return false; } Prof. Amr Goneid, AUC 26

Divide & Conquer Approach n Remember that this approach models to a recurrence relation: T(n) = 2 T(n-1) + 1 for n > 0 with T(0) = 1 leading to: T(n) = 2 n+1 -1 = O(2 n) = exponential time Can Dynamic Programming do Better? Prof. Amr Goneid, AUC 27

Dynamic Programming Approach Use a tabel t[i, j], i = 0. . n, j = 0. . m n Base case: set t[0, 0] = true and t[0, j] = false for (j != 0) n Recursive calls are constructed as follows: loop on i = 1 to n loop on j = 1 to m n test on Sum. Sub (w, i-1, j) is replaced by t[i, j] = t[i-1, j] n return Sum. Sub (w, i-1, j - wi) is replaced by t[i, j] = t[i-1, j] OR t[i-1, j – wi] Prof. Amr Goneid, AUC 28

Dynamic Programming Algorithm bool Sum. Sub (w , n , m) { 1. t[0, 0] = true; for (j = 1 to m) t[0, j] = false; 2. for (i = 1 to n) 3. for (j = 0 to m) i-1, 4. t[i, j] = t[i-1, j]; j - wi 5. if ((j-wi) >= 0) 6. t[i, j] = t[i-1, j] || t[i-1, j – wi]; 7. return t[n, m]; } Prof. Amr Goneid, AUC i-1, j i, j 29

Dynamic Programming Algorithm Analysis: costs O(1) + O(m) 2. costs O(n) 3. costs O(m) 4. costs O(1) 5. costs O(1) 6. costs O(1) 7. costs O(1) Hence, space complexity is O(nm) Time complexity is T(n) = O(m) + O(nm) = O(nm) 1. Prof. Amr Goneid, AUC 30

5. The (0/1) Knapsack Problem n Given n indivisible objects with positive integer weights W = {w 1, w 2. . . wn} and positive integer values V = {v 1, v 2. . . vn} and a knapsack of size (m) i=1 w 1 p 1 i=2 i=n w 2 wn ……. . m pn p 2 n Find the highest valued subset of objects with total weight at most (m) Prof. Amr Goneid, AUC 31

The Decision Instance n Assume that we have tried objects of type (1, 2, . . . , i -1) to fill the sack up to a capacity (j) with a maximum profit of P(i-1, j) n If j wi then P(i-1, j - wi) is the maximum profit if we remove the equivalent weight wi of an object of type (i). n By trying to add object (i), we expect the maximum profit to change to P(i-1, j - wi) + vi Prof. Amr Goneid, AUC 32

The Decision Instance n If this change is better, we do it, otherwise we leave things as they were, i. e. , P(i , j) = max { P(i-1, j) , P(i-1, j - wi) + vi } for j wi P(i , j) = P(i-1, j) for j < wi n The above instance can be solved for P(n , m) by initializing P(0, j) = 0 and successively computing P(1, j) , P(2, j). . . , P (n , j) for all 0 j m Prof. Amr Goneid, AUC 33

Divide & Conquer Approach Algorithm: int Knapsackr (int w[ ], int v[ ], int i, int j) { if (i == 0) return 0; else { int a = Knapsackr (w, v, i-1, j); if ((j - w[i]) >= 0) { int b = Knapsackr (w, v, i-1, j-w[i]) + v[i]; return (b > a? b : a); } else return a; } } Prof. Amr Goneid, AUC 34

Divide & Conquer Approach Analysis: T(n) = no. of calls to Knapsackr (w, v, n, m): n For n = 0, one main call, T(0) = 1 n For n > 0, one main call plus two calls each with n-1 n The recurrence relation is: T(n) = 2 T(n-1) + 1 for n > 0 with T(0) = 1 n Hence T(n) = 2 n+1 -1 = O(2 n) = exponential time Prof. Amr Goneid, AUC 35

Dynamic Programming Approach n The following approach will give the maximum profit, but not the collection of objects that produced this profit n Initialize P(0 , j) = 0 for 0 j m n Initialize P(i , 0) = 0 for 0 i n n for each object i from 1 to n do for a capacity j from 0 to m do P(i , j) = P(i-1 , j) if ( j >= wi) if (P(i-1 , j) < P(i-1, j - wi) + vi ) P(i , j) P(i-1 , j - wi) + vi Prof. Amr Goneid, AUC 36

DP Algorithm int Knapsackdp (int w[ ], int v[ ], int n, int m) { int p[N][M]; for (int j = 0; j <= m; j++) p[0][j] = 0; for (int i= 0; i <= n; i++) p[i][0] = 0; for (int i = 1; i <= n; i++) for (j = 0; j <= m; j++) { int a = p[i-1][j]; p[i][j] = a; if ((j-w[i]) >= 0) { int b = p[i-1][j-w[i]]+v[i]; if (b > a) p[i][j] = b; } } return p[n][m]; } Hence, space complexity is O(nm) Time complexity is T(n) = O(n) + O(m) + O(nm) = O(nm) Prof. Amr Goneid, AUC 37

Example: Knapsack capacity m = 5 item weight value ($) 1 2 12 2 1 10 3 3 20 4 2 15 Prof. Amr Goneid, AUC 38

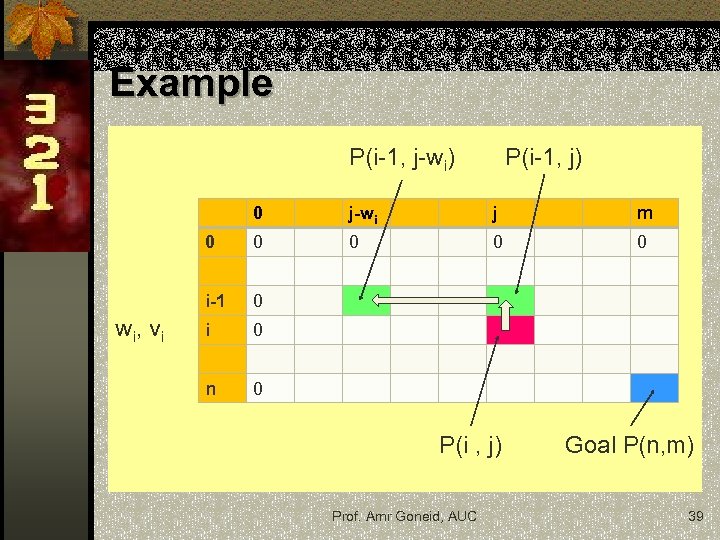Example P(i-1, j-wi) P(i-1, j) 0 j m 0 0 0 i-1 w i, v i j-wi 0 n 0 P(i , j) Prof. Amr Goneid, AUC Goal P(n, m) 39

Example. Prof. Amr Goneid, AUC 40

Exercises n Modify the previous Knapsack algorithm so that it could also list the objects contributing to the maximum profit. n Explain how to reduce the space complexity of the Knapsack problem to only O(m). You need only to find the maximum profit, not the actual collection of objects. Prof. Amr Goneid, AUC 41

Exercise: Longest Common Sequence Problem n Given two sequences A = {a 1, . . . , an} and B = {b 1, . . . , bm}. n Find the longest sequence that is a subsequence of both A and B. For example, if A = {aaadebcbac} and B = {abcadebcbec}, then {adebcb} is subsequence of length 6 of both sequences. n Give the recursive Divide & Conquer algorithm and the Dynamic programming algorithm together with their analyses n Hint: Let L(i, j) be the length of the longest common subsequence of {a 1, . . . , ai} and {b 1, . . . , bj}. If ai = bj then L(i, j) = L(i− 1, j − 1)+1. Otherwise, one can see that L(i, j) = max (L(i, j − 1), L(i − 1, j)). Prof. Amr Goneid, AUC 42

6. Minimum Cost Path n Given a cost matrix C[ ][ ] and a position (n, m) in C[ ][ ], find the cost of minimum cost path to reach (n , m) from (0, 0). n Each cell of the matrix represents a cost to traverse through that cell. Total cost of a path to reach (n, m) is the sum of all the costs on that path (including both source and destination). n From a given cell (i, j), You can only traverse down to cell (i+1, j), , right to cell (i, j+1) and diagonally to cell (i+1, j+1). Assume that all costs are positive integers Prof. Amr Goneid, AUC 43

Minimum Cost Path Example: what is the minimum cost path to (2, 2)? The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 3). n Optimal Substructure Minimum cost to reach (n, m) is “minimum of the 3 cells plus cost[n][m]“. i. e. , min. Cost(n, m) = min (min. Cost(n-1, m-1), min. Cost(n-1, m), min. Cost(n, m-1)) + C[n][m] Prof. Amr Goneid, AUC 44

Minimum Cost Path (D&Q) n Overlapping Subproblems: The recursive definition suggests a D&Q approach with overlapping subproblems: int Min. Cost(int C[ ][M], int n, int m) { if (n < 0 || m < 0) return ∞; else if (n == 0 && m == 0) return C[n][m]; else return C[n][m] + min( Min. Cost(C, n-1, m-1), Min. Cost(C, n-1, m), Min. Cost(C, n, m-1) ); } Anaysis: For m=n, T(n) = 3 T(n-1) + 3 for n > 0 with T(0) = 0 Hence T(n) = O(3 n) , exponential complexity Prof. Amr Goneid, AUC 45

Dynamic Programming Algorithm In the Dynamic Programming(DP) algorithm, recomputations of same subproblems can be avoided by constructing a temporary array T[ ][ ] in a bottom up manner. int min. Cost(int C[ ][M], int n, int m) Space complexity is O(nm) { int i, j; int T[N][M]; Time complexity is T[0][0] = C[0][0]; T(n) = O(n)+O(m) + /* Initialize first column */ O(nm) = O(nm) for (i = 1; i <= n; i++) T[i][0] = T[i-1][0] + C[i][0]; /* Initialize first row */ for (j = 1; j <= m; j++) T[0][j] = T[0][j-1] + C[0][j]; /* Construct rest of the array */ for (i = 1; i <= n; i++) for (j = 1; j <= m; j++) T[i][j] = min(T[i-1][j-1], T[i-1][j], T[i][j-1]) + C[i][j]; return T[n][m]; } Prof. Amr Goneid, AUC 46

7. Coin Change Problem n We want to make change for N cents, and we have infinite supply of each of S = {S 1 , S 2, …Sm} valued coins, how many ways can we make the change? (For simplicity's sake, the order does not matter. ) n Mathematically, how many ways can we express N as n For example, for N = 4, S = {1, 2, 3}, there are four solutions: {1, 1, 1, 1}, {1, 1, 2}, {2, 2}, {1, 3}. n We are trying to count the number of distinct sets. n Since order does not matter, we will impose that our solutions (sets) are all sorted in non-decreasing order (Thus, we are looking at sorted-set solutions: collections). Prof. Amr Goneid, AUC 47

Coin Change Problem n With S 1 < S 2 < …

D&Q Algorithm int count( int S[ ], int m, int n ) { // If n is 0 then there is 1 solution (do not include any coin) if (n == 0) return 1; // If n is less than 0 then no solution exists if (n < 0) return 0; // If there are no coins and n is greater than 0, then no solution if (m <=0 && n >= 1) return 0; // count is sum of solutions (i) including S[m-1] (ii) excluding // S[m-1] return count( S, m - 1, n ) + count( S, m, n-S[m-1] ); } The algorithm has exponential complexity. Prof. Amr Goneid, AUC 49

DP Algorithm int count( int S[ ], int m, int n ) { int i, j, x, y; int table[n+1][m]; // n+1 rows to include the case (n = 0) for (i=0; i < m; i++) table[0][i] = 1; // Fill for the case (n = 0) // Fill rest of the table enteries bottom up for (i = 1; i < n+1; i++) for (j = 0; j < m; j++) { x = (i-S[j] >= 0)? table[i - S[j]][j]: 0; // solutions including S[j] y = (j >= 1)? table[i][j-1]: 0; // solutions excluding S[j] table[i][j] = x + y; // total count } return table[n][m-1]; } Space comlexity is O(nm) Time comlexity is O(m) + O(nm) = O(nm) Prof. Amr Goneid, AUC 50

8. Optimal Binary Search Trees n Problem: Given a set of keys K 1 , K 2 , … , Kn and their corresponding search frequencies P 1 , P 2 , … , Pn , find a binary search tree for the keys such that the total search cost is minimum. n Remark: The problem is similar to that of the optimal merge trees (Huffman Coding) but more difficult because now: - Keys can exist in internal nodes - The binary search tree condition (Left < Parent < Right) is imposed Prof. Amr Goneid, AUC 51

(a) Example n A Binary Search Tree of 5 words: Word a am and if two Freq (tot 100) 22 18 20 30 10 n A Greedy Algorithm: Insert words in the tree in order of decreasing frequency of search. Prof. Amr Goneid, AUC 52

A Greedy BST n Insert (if) , (and) , (am) , (two) if 22 Level 1 30 a two and 10 20 2 3 4 18 am n Total Search Cost (100 searches) = 1*30 + 2*22 + 2* 10 + 3*20 + 4*18 = 226 Prof. Amr Goneid, AUC 53

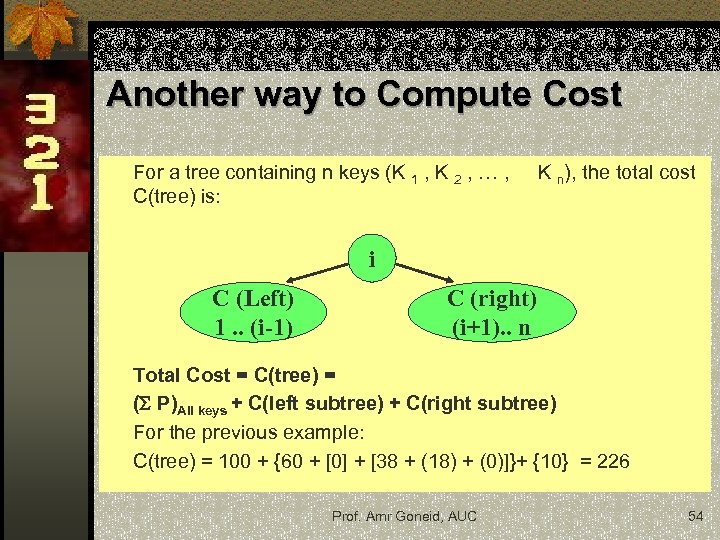Another way to Compute Cost For a tree containing n keys (K 1 , K 2 , … , C(tree) is: K n), the total cost i C (Left) 1. . (i-1) C (right) (i+1). . n Total Cost = C(tree) = ( P)All keys + C(left subtree) + C(right subtree) For the previous example: C(tree) = 100 + {60 + [0] + [38 + (18) + (0)]}+ {10} = 226 Prof. Amr Goneid, AUC 54

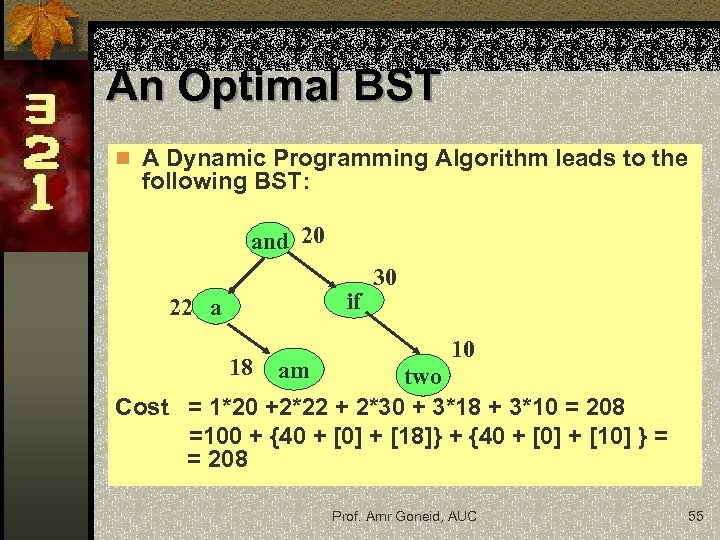An Optimal BST n A Dynamic Programming Algorithm leads to the following BST: and 20 if 22 a 18 am 30 10 two Cost = 1*20 +2*22 + 2*30 + 3*18 + 3*10 = 208 =100 + {40 + [0] + [18]} + {40 + [0] + [10] } = = 208 Prof. Amr Goneid, AUC 55

(b) Dynamic Programming Method n For n keys, we perform n-1 iterations 1 j n-1 n In each iteration (j), we compute the best way to build a sub-tree containing j+1 keys (K i , K i+1 , … , K i+j) for all possible BST combinations of such j+1 keys ( i. e. for 1 i n-j). n Each sub-tree is tried with one of the keys as the root and a minimum cost sub-tree is stored. n For a given iteration (j), we use previously stored values to determine the current best sub-tree. Prof. Amr Goneid, AUC 56

Simple Example n For 3 keys (A < B < C), we perform 2 iterations j = 1 , j = 2 n For j = 1, we build sub-trees using 2 keys. These come from i = 1, (A-B), and i = 2, (B-C). n For each of these combinations, we compute the least cost sub-tree, i. e. , the least cost of the two sub-trees (A*, B) and (A, B*) and the least cost of the two sub-trees (B*, C) and (B, C*) , where (*) denotes parent. Prof. Amr Goneid, AUC 57

Simple Example (Cont. ) n For j = 2, we build trees using 3 keys. These come from i = 1, (A-C). n For this combination, we compute the least cost tree of the trees (A*, (B-C)) , (A , B* , C) , ((A-B) , C*). This is done using previously computed least cost sub-trees. Prof. Amr Goneid, AUC 58

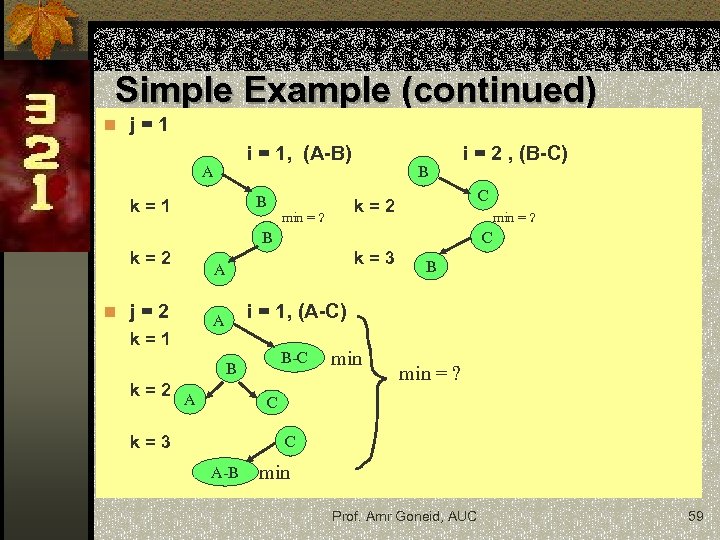Simple Example (continued) n j=1 i = 1, (A-B) A B k=1 B i = 2 , (B-C) C k=2 min = ? B k=2 n j=2 k=1 C k=3 A B i = 1, (A-C) A B-C B k=2 A min = ? C k=3 C A-B min Prof. Amr Goneid, AUC 59

(c) Example Revisited: Optimal BST for 5 keys n Iterations 1. . 2 Prof. Amr Goneid, AUC 60

Optimal BST for 5 keys n Iterations 3. . n-1 Prof. Amr Goneid, AUC 61

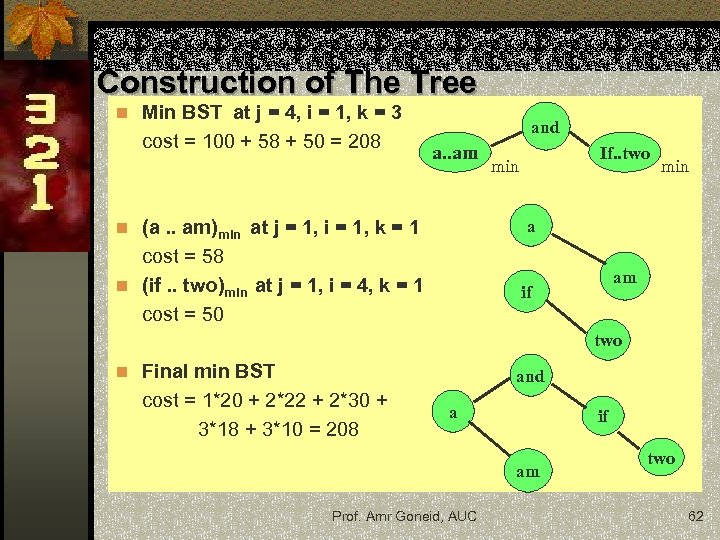Construction of The Tree n Min BST at j = 4, i = 1, k = 3 cost = 100 + 58 + 50 = 208 and a. . am If. . two min a n (a. . am)min at j = 1, i = 1, k = 1 cost = 58 n (if. . two)min at j = 1, i = 4, k = 1 cost = 50 am if two n Final min BST and cost = 1*20 + 2*22 + 2*30 + 3*18 + 3*10 = 208 a if am Prof. Amr Goneid, AUC two 62

(d) Complexity Analysis n Skeletal Algorithm: for j = 1 to n-1 do { // sub-tree has j+1 nodes for i = 1 to n-j do { // for each of the n-j sub-tree combinations for k = i to i+j do { find cost of each of the j+1 configurations and determine minimum cost } } } n T(n) = 1 j n-1 ( j + 1) (n – j) = O(n 3) , S(n) = O(n 2) Prof. Amr Goneid, AUC 63

Exercise n Find the optimal binary search tree for the following words with the associated frequencies: a (18) , and (22) , I (19) , it (20) , or (21) n Answer: Min cost = 20 + 2*43 + 3*37 = 217 it 20 21 22 or and 18 a I Prof. Amr Goneid, AUC 19 64

9. Dynamic Programming Algorithms for Graph Problems Various optimization graph problems have been solved using Dynamic Programming algorithms. Examples are: n Dijkstra's algorithm solves the single-source shortest path problem for a graph with nonnegative edge path costs n Floyd–Warshall algorithm for finding all pairs shortest paths in a weighted graph (with positive or negative edge weights) and also for finding transitive closure n The Bellman–Ford algorithm computes single-source shortest paths in a weighted digraph for graphs with negative edge weights. These will be discussed later under “Graph Algorithms”. Prof. Amr Goneid, AUC 65

10. Comparison with Greedy and Divide & Conquer Methods n Greedy vs. DP : n n n Both are optimization techniques, building solutions from a collection of choices of individual elements. The greedy method computes its solution by making its choices in a serial forward fashion, never looking back or revising previous choices. DP computes its solution bottom up by synthesizing them from smaller subsolutions, and by trying many possibilities and choices before it arrives at the optimal set of choices. There is no a priori test by which one can tell if the Greedy method will lead to an optimal solution. By contrast, there is a test for DP, called The Principle of Optimality Prof. Amr Goneid, AUC 66

Comparison with Greedy and Divide & Conquer Methods n D&Q vs. DP: Both techniques split their input into parts, find subsolutions to the parts, and synthesize larger solutions from smaller ones. n D&Q splits input at pre-specified deterministic points (e. g. , always in the middle) n DP splits input at every possible split point rather than at pre-specified points. After trying all split points, it determines which split point is optimal. n Prof. Amr Goneid, AUC 67