взаимосвязи качественных признаков.ppt
- Количество слайдов: 55
 АНАЛИЗ ВЗАИМОСВЯЗЕЙ КАЧЕСТВЕННЫХ ПРИЗНАКОВ
АНАЛИЗ ВЗАИМОСВЯЗЕЙ КАЧЕСТВЕННЫХ ПРИЗНАКОВ
 Типы качественных признаков l Качественные признаки делятся на два типа: ранговые и номинальные: l l Ранговые признаки представлены упорядоченными категориями, Номинальные признаки представлены неупорядоченными категориями.
Типы качественных признаков l Качественные признаки делятся на два типа: ранговые и номинальные: l l Ранговые признаки представлены упорядоченными категориями, Номинальные признаки представлены неупорядоченными категориями.
 Взаимосвязь ранговых признаков
Взаимосвязь ранговых признаков
 Взаимосвязь ранговых признаков Меры взаимосвязи между парой ранговых признаков называются коэффициентами ранговой корреляции. Эти коэффициенты строятся так, чтобы выполнялись следующие свойства: l l 1. Если ранжированные ряды по обоим признакам полностью совпадают, то коэффициент ранговой корреляции равен +1, что означает полную положительную корреляцию.
Взаимосвязь ранговых признаков Меры взаимосвязи между парой ранговых признаков называются коэффициентами ранговой корреляции. Эти коэффициенты строятся так, чтобы выполнялись следующие свойства: l l 1. Если ранжированные ряды по обоим признакам полностью совпадают, то коэффициент ранговой корреляции равен +1, что означает полную положительную корреляцию.
 Взаимосвязь ранговых признаков 2. 3. Если объекты в обоих рядах расположены в противоположном порядке, коэффициент равен – 1, что означает полную отрицательную корреляцию. Нулевое значение коэффициента означает отсутствие соответствия между ранжированными рядами.
Взаимосвязь ранговых признаков 2. 3. Если объекты в обоих рядах расположены в противоположном порядке, коэффициент равен – 1, что означает полную отрицательную корреляцию. Нулевое значение коэффициента означает отсутствие соответствия между ранжированными рядами.
 Взаимосвязь ранговых признаков 3. В остальных ситуациях значения коэффициента заключены в интервале [– 1, +1]; при этом возрастание абсолютного значения коэффициента корреляции от 0 до 1 характеризует увеличение соответствия между двумя ранжированными рядами.
Взаимосвязь ранговых признаков 3. В остальных ситуациях значения коэффициента заключены в интервале [– 1, +1]; при этом возрастание абсолютного значения коэффициента корреляции от 0 до 1 характеризует увеличение соответствия между двумя ранжированными рядами.
 Коэффициенты ранговой корреляции l l Наиболее известны коэффициенты ранговой корреляции Спирмена и Кендалла . Их значения достаточно близки, но коэффициент Кендалла дает более осторожную оценку корреляции, чем коэффициент Спирмена (числовое значение всегда меньше, чем значение ).
Коэффициенты ранговой корреляции l l Наиболее известны коэффициенты ранговой корреляции Спирмена и Кендалла . Их значения достаточно близки, но коэффициент Кендалла дает более осторожную оценку корреляции, чем коэффициент Спирмена (числовое значение всегда меньше, чем значение ).
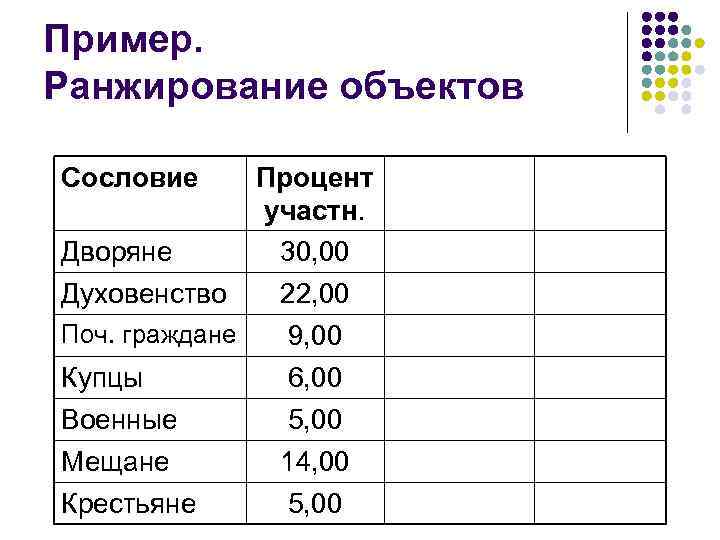 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Военные Мещане 5, 00 14, 00 Крестьяне 5, 00
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Военные Мещане 5, 00 14, 00 Крестьяне 5, 00
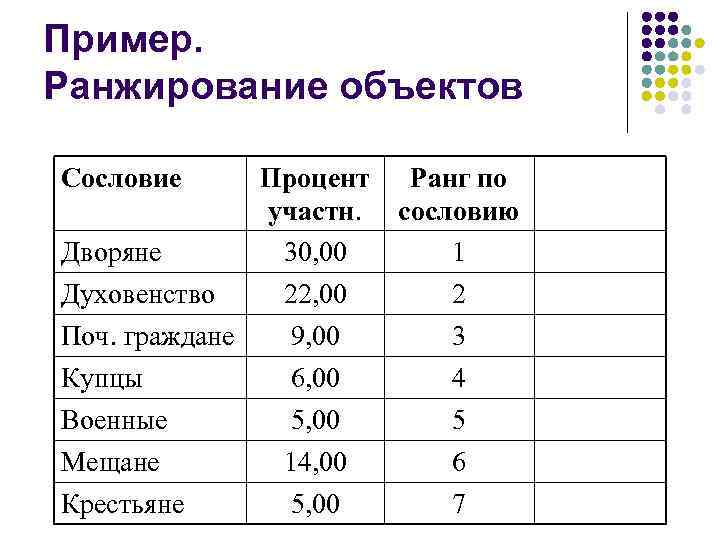 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию 1 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию 1 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
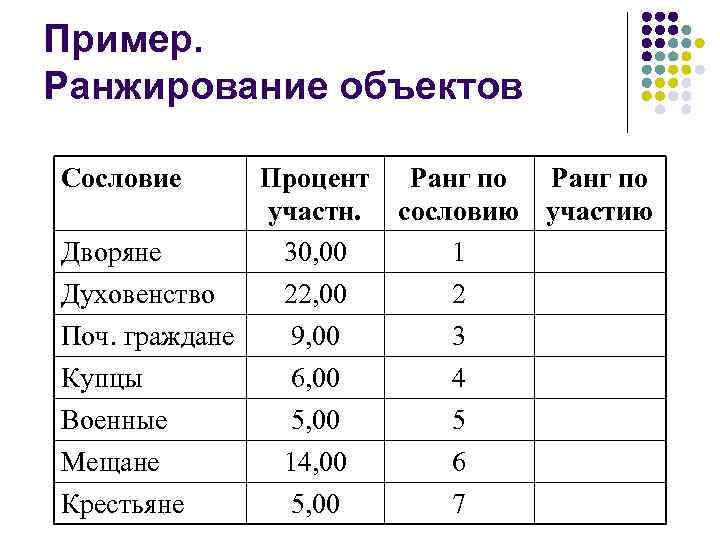 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
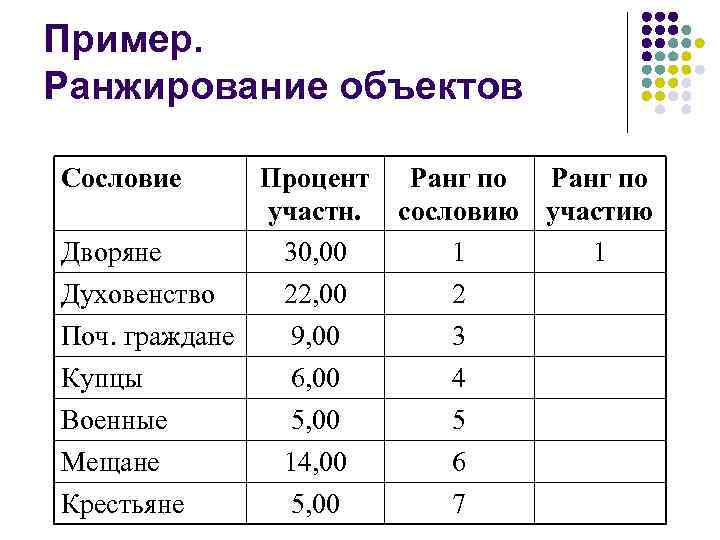 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
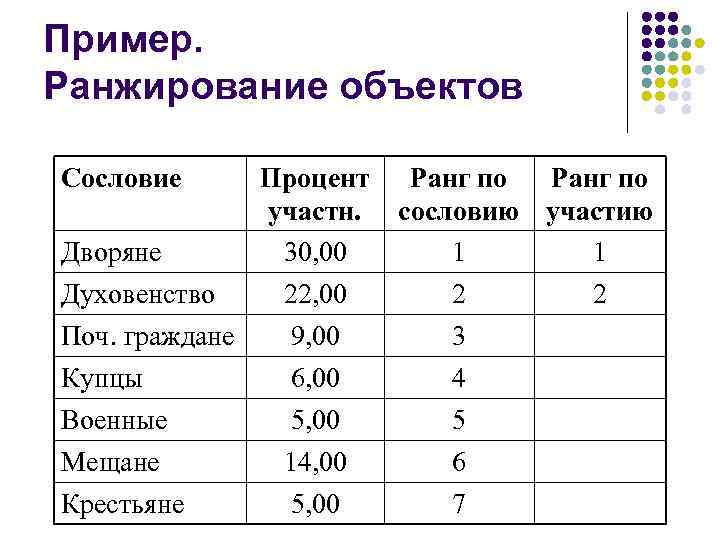 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7
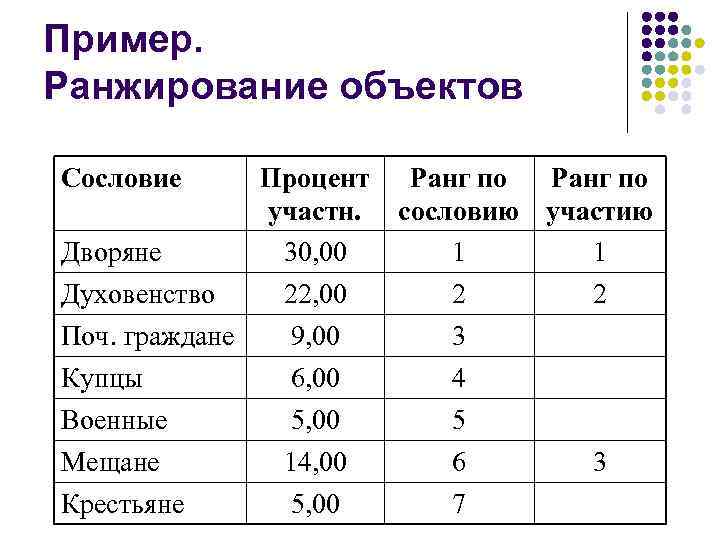 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7 3
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7 3
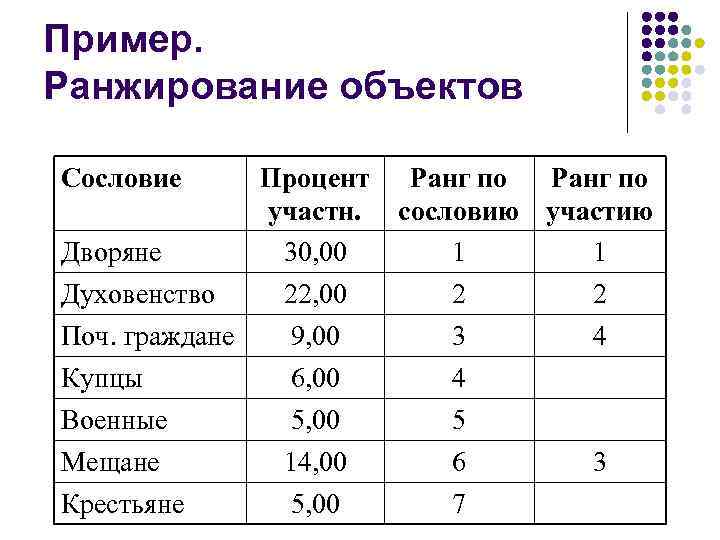 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7 3
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 4 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7 3
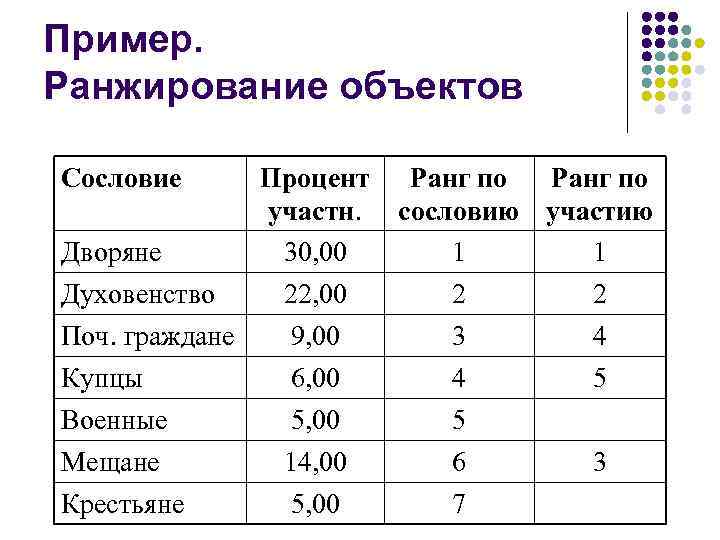 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 4 5 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7 3
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 4 5 Военные Мещане 5, 00 14, 00 5 6 Крестьяне 5, 00 7 3
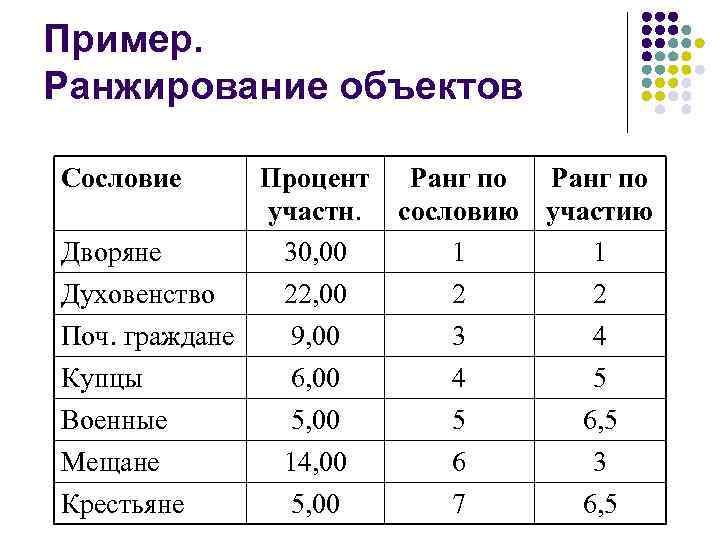 Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 4 5 Военные Мещане 5, 00 14, 00 5 6 6, 5 3 Крестьяне 5, 00 7 6, 5
Пример. Ранжирование объектов Сословие Процент участн. Дворяне 30, 00 Духовенство 22, 00 Поч. граждане 9, 00 Купцы 6, 00 Ранг по сословию участию 1 1 2 2 3 4 4 5 Военные Мещане 5, 00 14, 00 5 6 6, 5 3 Крестьяне 5, 00 7 6, 5
 Ранжирование объектов l Если два (или больше) объектов получают одинаковые ранги, такие объекты называют связанными. Ранг связанных объектов равен среднему значению рангов, которые имели бы эти объекты, если бы они были различны. l Например, если связанными оказались 3 -й, 4 -й и 5 -й объекты в ранжированном ряду, то каждому из них приписывается ранг – ?
Ранжирование объектов l Если два (или больше) объектов получают одинаковые ранги, такие объекты называют связанными. Ранг связанных объектов равен среднему значению рангов, которые имели бы эти объекты, если бы они были различны. l Например, если связанными оказались 3 -й, 4 -й и 5 -й объекты в ранжированном ряду, то каждому из них приписывается ранг – ?
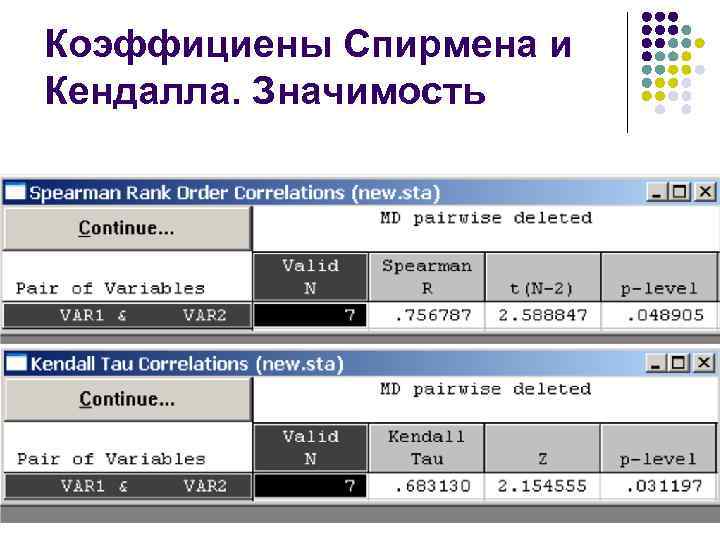 Коэффициены Спирмена и Кендалла. Значимость
Коэффициены Спирмена и Кендалла. Значимость
 Коэффициены Спирмена и Кендалла. Значимость l l Проверка значимости коэффициентов ранговой корреляции проходит по той же схеме, что и проверка значимости коэффициентов корреляции для количественных признаков. Вычисляется величина t-статистики и соответствующая ей величина p – вероятность ошибки (случайного получения в выборке таких коэффициентов при отсутствии корреляции в генеральной совокупности).
Коэффициены Спирмена и Кендалла. Значимость l l Проверка значимости коэффициентов ранговой корреляции проходит по той же схеме, что и проверка значимости коэффициентов корреляции для количественных признаков. Вычисляется величина t-статистики и соответствующая ей величина p – вероятность ошибки (случайного получения в выборке таких коэффициентов при отсутствии корреляции в генеральной совокупности).
 Коэффициены Спирмена и Кендалла. Значимость l l Если значение t достаточно велико (| t | >2), а вероятность p, соответственно, достаточно мала (p <0, 05) коэффициент ранговой корреляции можно считать статистически значимым, т. е. гипотеза о независимости признаков в генеральной совокупности должна быть отклонена. Иначе – коэффициент ранговой корреляции считается статистически незначимым.
Коэффициены Спирмена и Кендалла. Значимость l l Если значение t достаточно велико (| t | >2), а вероятность p, соответственно, достаточно мала (p <0, 05) коэффициент ранговой корреляции можно считать статистически значимым, т. е. гипотеза о независимости признаков в генеральной совокупности должна быть отклонена. Иначе – коэффициент ранговой корреляции считается статистически незначимым.
 Применение ранговой корреляции l Какие коэффициенты можно использовать для измерения силы связи между ранговым и количественным признаками? l Как должны быть преобразованы значения количественного признака?
Применение ранговой корреляции l Какие коэффициенты можно использовать для измерения силы связи между ранговым и количественным признаками? l Как должны быть преобразованы значения количественного признака?
 Взаимосвязь номинальных признаков Таблицы сопряженности
Взаимосвязь номинальных признаков Таблицы сопряженности
 Таблицы сопряженности l В статистическом анализе существуют различные методы, позволяющие изучать взаимосвязи номинальных признаков. l Наиболее популярным из них является метод построения таблиц сопряженности (кросс-табуляция).
Таблицы сопряженности l В статистическом анализе существуют различные методы, позволяющие изучать взаимосвязи номинальных признаков. l Наиболее популярным из них является метод построения таблиц сопряженности (кросс-табуляция).
 Таблицы сопряженности l l Таблицей сопряженности называется прямоугольная таблица, по строкам которой указываются категории одного признака, а по столбцам – категории другого. Каждый объект совокупности "попадает" в какую-либо из клеток этой таблицы в соответствии с тем, к какой категории он относится по каждому из двух признаков.
Таблицы сопряженности l l Таблицей сопряженности называется прямоугольная таблица, по строкам которой указываются категории одного признака, а по столбцам – категории другого. Каждый объект совокупности "попадает" в какую-либо из клеток этой таблицы в соответствии с тем, к какой категории он относится по каждому из двух признаков.
 Таблицы сопряженности l l В каждой клетке таблицы находится частота совместной встречаемости соответствующих категорий двух признаков. Характер распределения частот внутри таблицы позволяет судить о том, существует ли связь между признаками.
Таблицы сопряженности l l В каждой клетке таблицы находится частота совместной встречаемости соответствующих категорий двух признаков. Характер распределения частот внутри таблицы позволяет судить о том, существует ли связь между признаками.
 Таблицы сопряженности l Что означает связь между номинальными признаками? l Например. Что означает связь между: l l социальным статусом и партийной принадлежностью? образованием и родом занятий?
Таблицы сопряженности l Что означает связь между номинальными признаками? l Например. Что означает связь между: l l социальным статусом и партийной принадлежностью? образованием и родом занятий?
 Таблицы сопряженности l Формально, связь номинальных признаков понимается как более частая (или наоборот, более редкая) совместная встречаемость отдельных комбинаций категорий по сравнению с ожидаемой встречаемостью – ситуацией чисто случайного распределения объектов по категориям двух признаков.
Таблицы сопряженности l Формально, связь номинальных признаков понимается как более частая (или наоборот, более редкая) совместная встречаемость отдельных комбинаций категорий по сравнению с ожидаемой встречаемостью – ситуацией чисто случайного распределения объектов по категориям двух признаков.
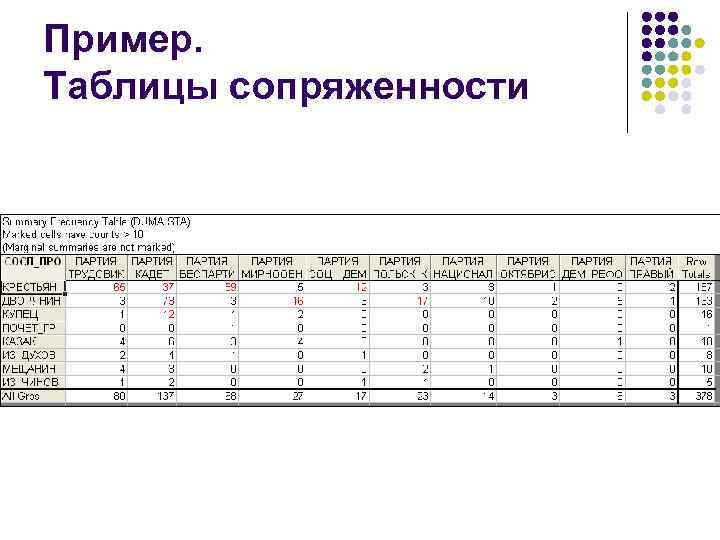 Пример. Таблицы сопряженности
Пример. Таблицы сопряженности
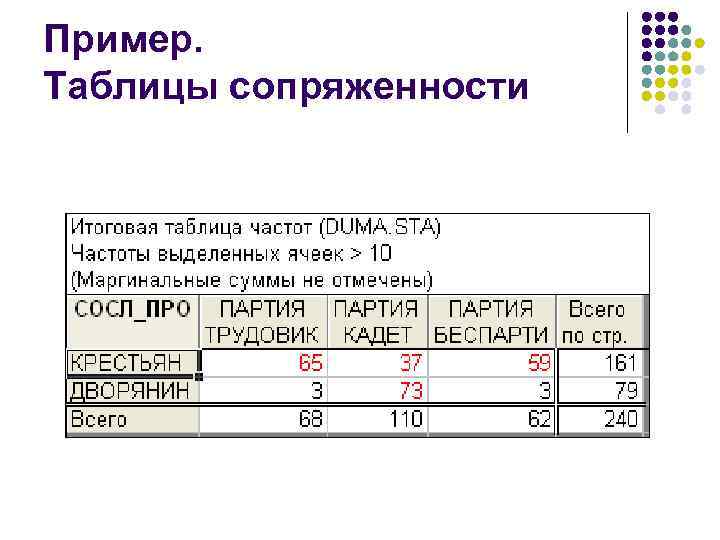 Пример. Таблицы сопряженности
Пример. Таблицы сопряженности
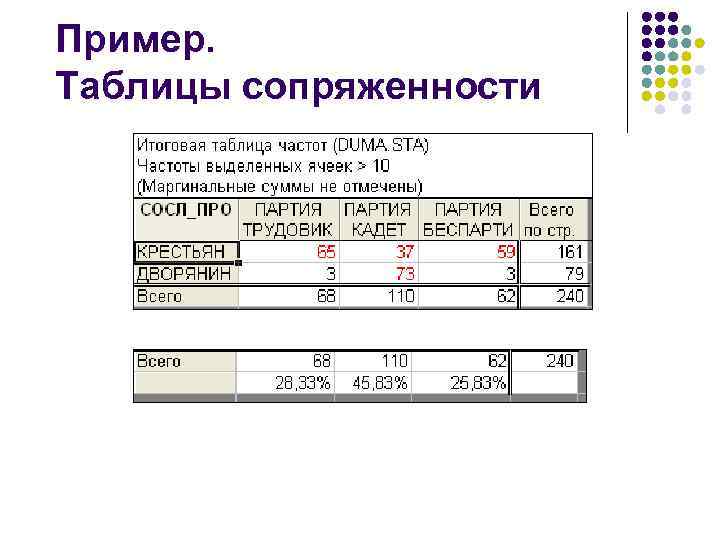 Пример. Таблицы сопряженности
Пример. Таблицы сопряженности
 Пример. Таблицы сопряженности l l В таблице представлены данные для 240 депутатов; среди них 79 человек (т. е. 1/3, или 33%) являются дворянами. Если бы распределение по фракциям не зависело от социального происхождения, то доля дворян и среди кадетов, и среди трудовиков, и среди беспартийных также составляла бы 1/3 численности каждой из этих фракций.
Пример. Таблицы сопряженности l l В таблице представлены данные для 240 депутатов; среди них 79 человек (т. е. 1/3, или 33%) являются дворянами. Если бы распределение по фракциям не зависело от социального происхождения, то доля дворян и среди кадетов, и среди трудовиков, и среди беспартийных также составляла бы 1/3 численности каждой из этих фракций.
 Пример. Таблицы сопряженности Например, из общего числа трудовиков (68 человек) 1/3, или 23 человека "должны были бы" являться дворянами.
Пример. Таблицы сопряженности Например, из общего числа трудовиков (68 человек) 1/3, или 23 человека "должны были бы" являться дворянами.
 Пример. Таблицы сопряженности Например, из общего числа трудовиков (68 человек) 1/3, или 23 человека "должны были бы" являться дворянами. Если же взглянуть на реальное число трудовиков-дворян, то окажется, что их всего трое, то есть значительно меньше, чем ожидалось.
Пример. Таблицы сопряженности Например, из общего числа трудовиков (68 человек) 1/3, или 23 человека "должны были бы" являться дворянами. Если же взглянуть на реальное число трудовиков-дворян, то окажется, что их всего трое, то есть значительно меньше, чем ожидалось.
 Пример. Таблицы сопряженности В партии кадетов (которых было 110 чел. ) тоже должно было быть 1/3 дворян, то есть 37 человек.
Пример. Таблицы сопряженности В партии кадетов (которых было 110 чел. ) тоже должно было быть 1/3 дворян, то есть 37 человек.
 Пример. Таблицы сопряженности В партии кадетов (которых было 110 чел. ) тоже должно было быть 1/3 дворян, то есть 37 человек. Однако в действительности дворян–кадетов было 73 человека, то есть вдвое больше, чем ожидалось бы.
Пример. Таблицы сопряженности В партии кадетов (которых было 110 чел. ) тоже должно было быть 1/3 дворян, то есть 37 человек. Однако в действительности дворян–кадетов было 73 человека, то есть вдвое больше, чем ожидалось бы.
 Пример. Таблицы сопряженности
Пример. Таблицы сопряженности
 Проверка гипотезы о независимости признаков
Проверка гипотезы о независимости признаков
 Проверка гипотезы о независимости признаков l Для проверки гипотезы о независимости признаков надо сравнить таблицу реальных частот с таблицей ожидаемых частот (т. е. частот, соответствующих гипотезе, что два изучаемых признака независимы).
Проверка гипотезы о независимости признаков l Для проверки гипотезы о независимости признаков надо сравнить таблицу реальных частот с таблицей ожидаемых частот (т. е. частот, соответствующих гипотезе, что два изучаемых признака независимы).
 Проверка гипотезы о независимости признаков l Для этого надо подсчитать суммарное расхождение между таблицами: сумму квадратов разностей между реальными и ожидаемыми частотами по всем клеткам таблиц. l Если таблицы совпадают, каково суммарное расхождение между ними?
Проверка гипотезы о независимости признаков l Для этого надо подсчитать суммарное расхождение между таблицами: сумму квадратов разностей между реальными и ожидаемыми частотами по всем клеткам таблиц. l Если таблицы совпадают, каково суммарное расхождение между ними?
 Проверка гипотезы о независимости признаков l Чем больше суммарное расхождение между таблицами, тем меньше вероятность гипотезы (нулевой гипотезы) о независимости признаков.
Проверка гипотезы о независимости признаков l Чем больше суммарное расхождение между таблицами, тем меньше вероятность гипотезы (нулевой гипотезы) о независимости признаков.
 Проверка гипотезы о независимости признаков l l Суммарное расхождение, или сумма квадратов разностей реальных и ожидаемых частот по всем клеткам таблицы обозначается Хи-квадрат (X 2). Для каждого значения Хи-квадрат известна вероятность p того, что это значение может быть получено случайно в выборке из генеральной совокупности, в которой признаки независимы.
Проверка гипотезы о независимости признаков l l Суммарное расхождение, или сумма квадратов разностей реальных и ожидаемых частот по всем клеткам таблицы обозначается Хи-квадрат (X 2). Для каждого значения Хи-квадрат известна вероятность p того, что это значение может быть получено случайно в выборке из генеральной совокупности, в которой признаки независимы.
 Проверка гипотезы о независимости признаков l l Если вероятность p, соответствующая величине Хи-квадрат, достаточно мала (p < 0, 05), это свидетельствует о том, что гипотеза о независимости признаков отклоняется и связь между ними является статистически значимой. Если p больше выбранного уровня (0, 05), гипотеза о независимости признаков не отклоняется и связь между ними является статистически незначимой.
Проверка гипотезы о независимости признаков l l Если вероятность p, соответствующая величине Хи-квадрат, достаточно мала (p < 0, 05), это свидетельствует о том, что гипотеза о независимости признаков отклоняется и связь между ними является статистически значимой. Если p больше выбранного уровня (0, 05), гипотеза о независимости признаков не отклоняется и связь между ними является статистически незначимой.
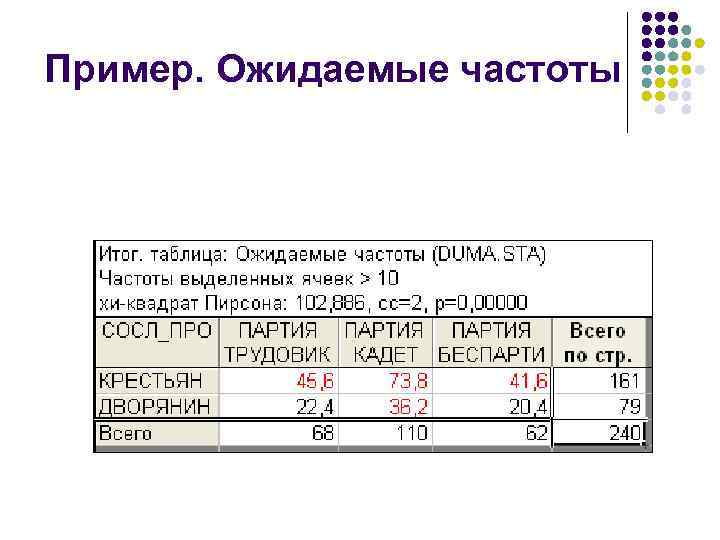 Пример. Ожидаемые частоты
Пример. Ожидаемые частоты
 Проверка гипотезы о независимости признаков l В заголовке таблицы ожидаемых частот приводятся: l l l значение X 2, которое равно 103, и соответствующее ему значение вероятности (p = 0, 0000), которое практически равно нулю. Следовательно, связь между признаками является статистически значимой? незначимой?
Проверка гипотезы о независимости признаков l В заголовке таблицы ожидаемых частот приводятся: l l l значение X 2, которое равно 103, и соответствующее ему значение вероятности (p = 0, 0000), которое практически равно нулю. Следовательно, связь между признаками является статистически значимой? незначимой?
 Коэффициенты взаимосвязи номинальных признаков
Коэффициенты взаимосвязи номинальных признаков
 Коэффициенты взаимосвязи номинальных признаков l l При отсутствии связи величина Хи-квадрат равна нулю, и это значение является минимальным. Существует ли максимальное значение для Хи-квадрат?
Коэффициенты взаимосвязи номинальных признаков l l При отсутствии связи величина Хи-квадрат равна нулю, и это значение является минимальным. Существует ли максимальное значение для Хи-квадрат?
 Коэффициенты взаимосвязи номинальных признаков l l Значимая величина Хи-квадрат является свидетельством связи между двумя признаками, но не имеет общего для всех таблиц сопряженности максимального значения. Более того, так как Хи-квадрат зависит от числа клеток таблицы, невозможно сравнивать между собой значения этой величины для таблиц с разным числом строк и столбцов.
Коэффициенты взаимосвязи номинальных признаков l l Значимая величина Хи-квадрат является свидетельством связи между двумя признаками, но не имеет общего для всех таблиц сопряженности максимального значения. Более того, так как Хи-квадрат зависит от числа клеток таблицы, невозможно сравнивать между собой значения этой величины для таблиц с разным числом строк и столбцов.
 Коэффициенты взаимосвязи номинальных признаков l Как же измерить силу этой связи? l Необходим коэффициент, который, подобно коэффициенту корреляции, имел бы фиксированный максимум в случае максимальной связи и позволял бы сравнивать между собой разные таблицы.
Коэффициенты взаимосвязи номинальных признаков l Как же измерить силу этой связи? l Необходим коэффициент, который, подобно коэффициенту корреляции, имел бы фиксированный максимум в случае максимальной связи и позволял бы сравнивать между собой разные таблицы.
 Коэффициент Крамера l l l Одним из коэффициентов, удовлетворяющих этим требованиям, является коэффициент Крамера V. Базируясь на значении Хи-квадрат, коэффициент Крамера позволяет измерять силу связи между двумя номинальными признаками. Коэффициент Крамера принимает значения от 0 до 1, т. е. от полного отсутствия связи до максимально сильной связи.
Коэффициент Крамера l l l Одним из коэффициентов, удовлетворяющих этим требованиям, является коэффициент Крамера V. Базируясь на значении Хи-квадрат, коэффициент Крамера позволяет измерять силу связи между двумя номинальными признаками. Коэффициент Крамера принимает значения от 0 до 1, т. е. от полного отсутствия связи до максимально сильной связи.
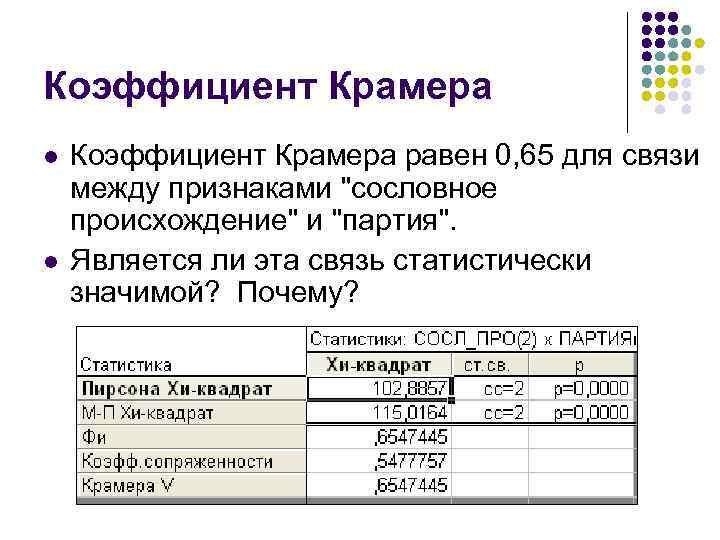 Коэффициент Крамера l l Коэффициент Крамера равен 0, 65 для связи между признаками "сословное происхождение" и "партия". Является ли эта связь статистически значимой? Почему?
Коэффициент Крамера l l Коэффициент Крамера равен 0, 65 для связи между признаками "сословное происхождение" и "партия". Является ли эта связь статистически значимой? Почему?
 Коэффициент Крамера l Коэффициент Крамера можно использовать для сравнения силы связи одного признака с несколькими другими.
Коэффициент Крамера l Коэффициент Крамера можно использовать для сравнения силы связи одного признака с несколькими другими.
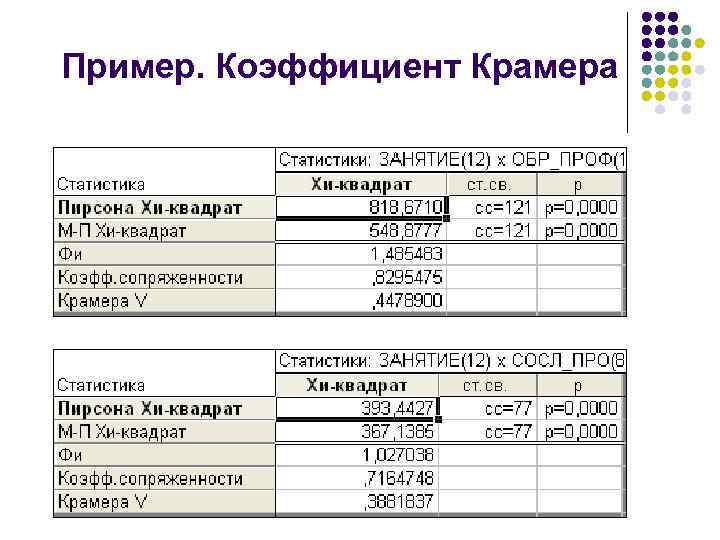 Пример. Коэффициент Крамера
Пример. Коэффициент Крамера
 Заключение 1. 2. 3. Методы измерения связи различаются для количественных, ранговых и номинальных признаков. Величины мер связи признаков различной природы не сравнимы между собой. Если требуется измерить связь между двумя признаками разной природы, то для этого обычно используют меры зависимости, пригодные для низшего уровня измерения.
Заключение 1. 2. 3. Методы измерения связи различаются для количественных, ранговых и номинальных признаков. Величины мер связи признаков различной природы не сравнимы между собой. Если требуется измерить связь между двумя признаками разной природы, то для этого обычно используют меры зависимости, пригодные для низшего уровня измерения.
 Заключение l l При этом следует учитывать, что возникают потери исходной информации, ее "огрубление". Однако такое огрубление иногда полезно, поскольку позволяет количественные данные с грубыми ошибками трактовать как ранговые или даже номинальные. Уменьшение точности при этом компенсируется повышением надежности данных.
Заключение l l При этом следует учитывать, что возникают потери исходной информации, ее "огрубление". Однако такое огрубление иногда полезно, поскольку позволяет количественные данные с грубыми ошибками трактовать как ранговые или даже номинальные. Уменьшение точности при этом компенсируется повышением надежности данных.
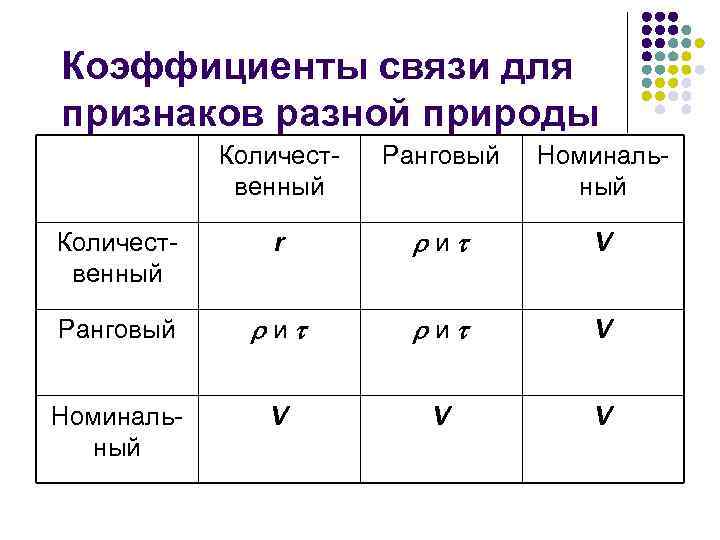 Коэффициенты связи для признаков разной природы Количественный Ранговый Номинальный Количественный r и V Ранговый и и V Номинальный V V V
Коэффициенты связи для признаков разной природы Количественный Ранговый Номинальный Количественный r и V Ранговый и и V Номинальный V V V


