Анализ временных рядов Метод Бокса-Дженкинса Модели одномерных

Анализ временных рядов Метод Бокса-Дженкинса

Модели одномерных временных рядов • АРСС (ARMA) для стационарных временных рядов • Процесс авторегрессии (AR) и его свойства • Процесс скользящего среднего (MA) и его свойства

«Белый шум» • Прежде всего введем «белого шума» . Будем обозначать его t. • Последовательность наблюдений случайной величины t будем называть «белым шумом» , если:

Пусть анализируемый процесс является стационарным • (См. определение стационарного процесса) • При анализе ARMA процессов важное значение имеют: – выборочная автокорреляционная функция (ACF) – выборочная частная автокорреляционная функция (PACF)

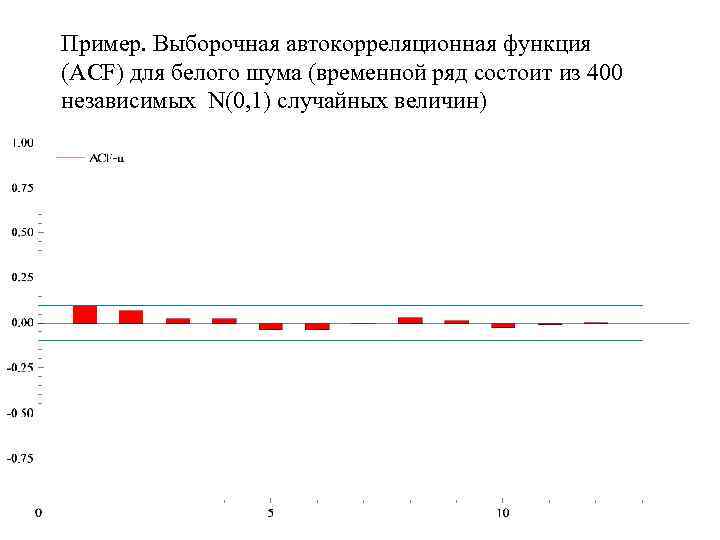
Пример. Выборочная автокорреляционная функция (ACF) для белого шума (временной ряд состоит из 400 независимых N(0, 1) случайных величин)

Выборочная частная автокорреляционная функция (PACF) • Коэффициент частной автокорреляции , определяется как оценка параметра авторегрессии k-го порядка

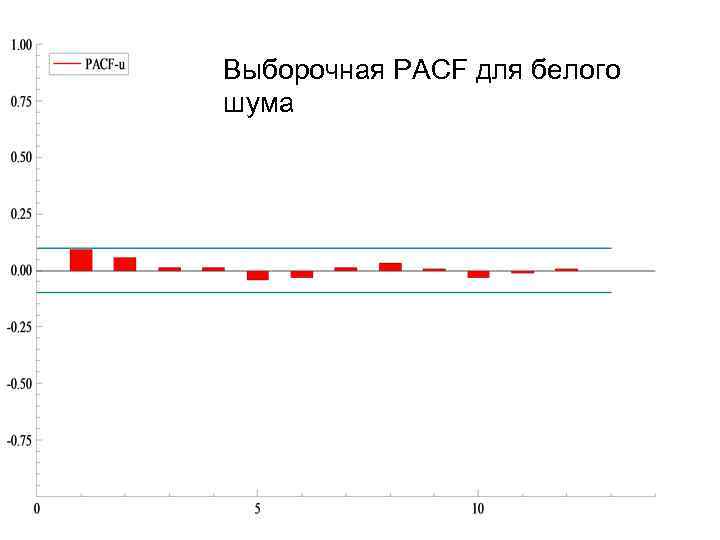
Выборочная PACF для белого шума

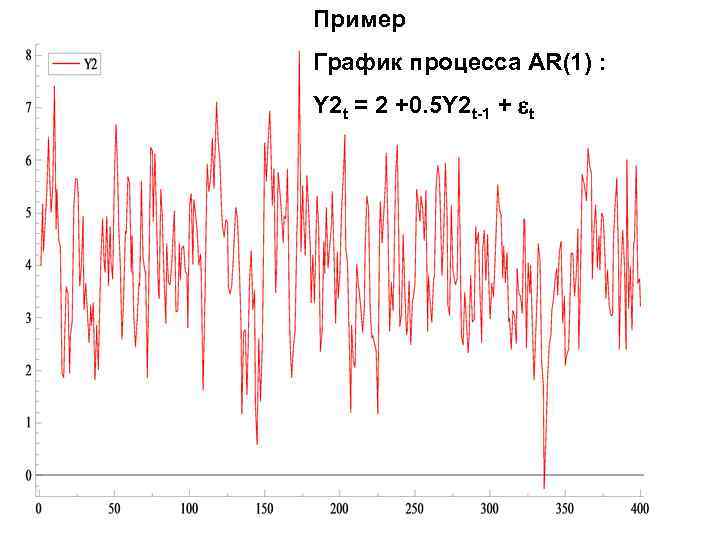
Пример График процесса AR(1) : Y 2 t = 2 +0. 5 Y 2 t-1 + t

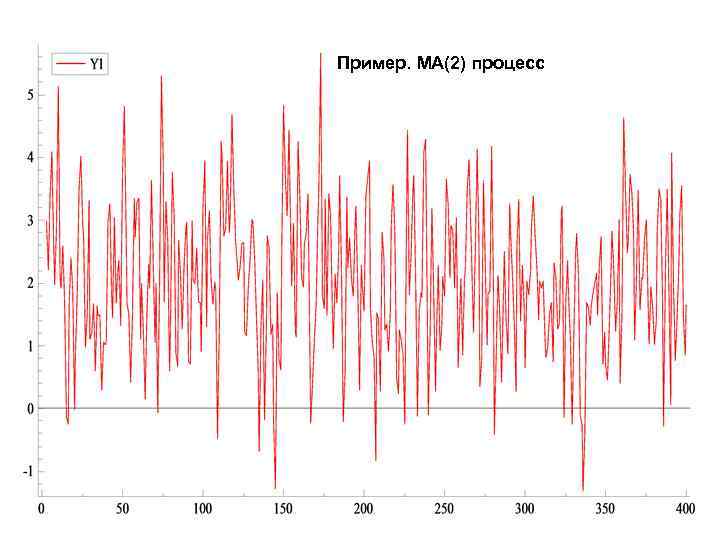
Пример. MA(2) процесс

Процесс авторегрессии – скользящего среднего ARMA • Если временной ряд Y порождается процессом ARMA (p, q), то он может быть записан в виде:

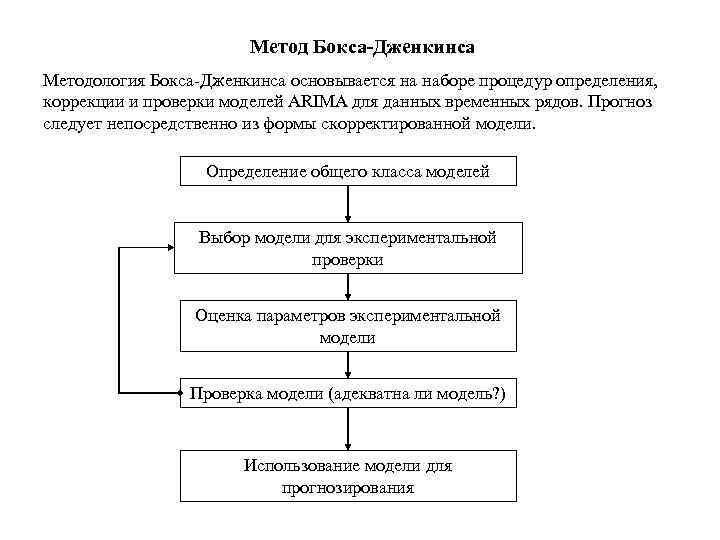
Метод Бокса-Дженкинса Методология Бокса-Дженкинса основывается на наборе процедур определения, коррекции и проверки моделей ARIMA для данных временных рядов. Прогноз следует непосредственно из формы скорректированной модели. Определение общего класса моделей Выбор модели для экспериментальной проверки Оценка параметров экспериментальной модели Проверка модели (адекватна ли модель? ) Использование модели для прогнозирования

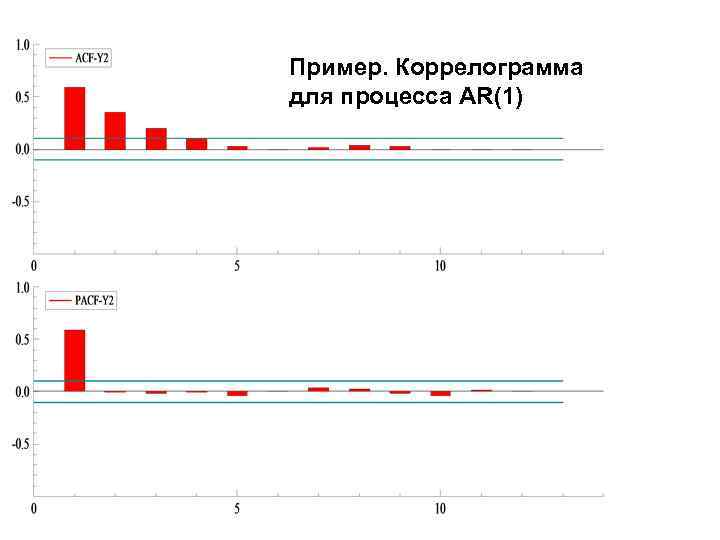
Пример. Коррелограмма для процесса AR(1)

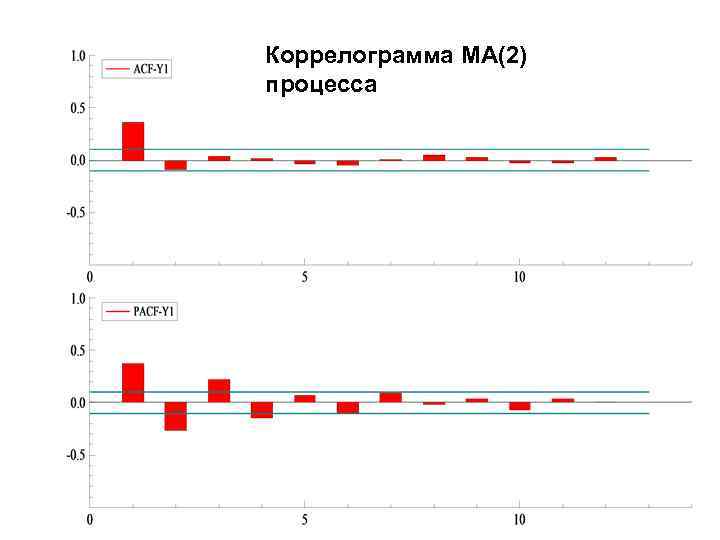
Коррелограмма MA(2) процесса

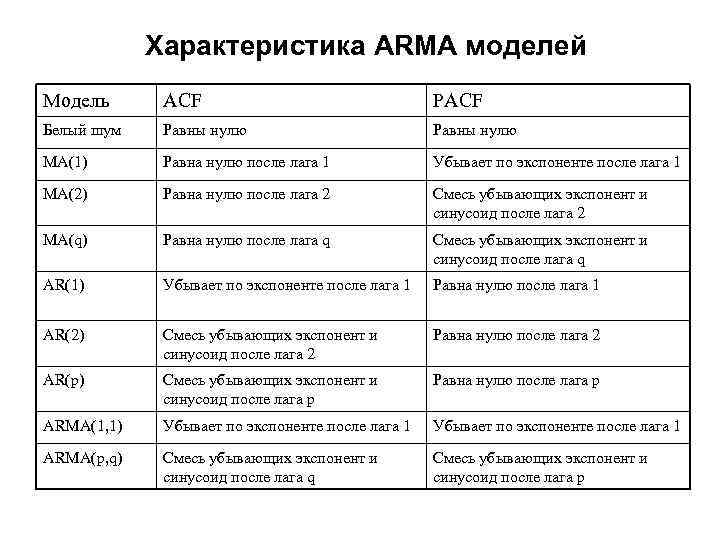
Характеристика ARMA моделей Модель ACF PACF Белый шум Равны нулю MA(1) Равна нулю после лага 1 Убывает по экспоненте после лага 1 MA(2) Равна нулю после лага 2 Смесь убывающих экспонент и синусоид после лага 2 MA(q) Равна нулю после лага q Смесь убывающих экспонент и синусоид после лага q AR(1) Убывает по экспоненте после лага 1 Равна нулю после лага 1 AR(2) Смесь убывающих экспонент и синусоид после лага 2 Равна нулю после лага 2 AR(p) Смесь убывающих экспонент и синусоид после лага p Равна нулю после лага p ARMA(1, 1) Убывает по экспоненте после лага 1 ARMA(p, q) Смесь убывающих экспонент и синусоид после лага q Смесь убывающих экспонент и синусоид после лага p

Реализация стратегии разработки модели Этап 1. Определение модели 1. На этапе определения модели следует выяснить, является ли ряд стационарным, то есть изменяются ли значения ряда в окрестностях некоторого фиксированного уровня. Для этого полезно посмотреть на график временного ряда и график выборочной автокорреляционной функции. Временные ряды не являются стационарными, если присутствует тренд, рост или спад. Если ряд не является стационарным его предварительно необходимо преобразовать в стационарный. 2. После того как получен стационарный ряд определяют общие характеристики модели. Так как при определении параметров ARMA на основе ACF и PACF имеет место некоторая неоднозначность, начальный выбор рассматривается как пробный. При равных условиях всегда следует отдавать предпочтение более простой модели.

Этап 2. Оценка модели 1. После того как пробная модель будет выбрана, необходимо выполнить оценку ее параметров. В общем случае для реализации этой процедуры должен применяться нелинейный метод наименьших квадратов. В результате находят оценки коэффициентов модели, их стандартные ошибки, t-статистики. 2. Вычисляется остаточная дисперсия и остаточная среднеквадратическая ошибка. Стандартная ошибка используется для сравнения различных моделей. Кроме того, она используется при построении доверительных интервалов при прогнозировании.

Этап 3. Проверка модели Прежде чем приступить к прогнозированию модель должна пройти проверку на адекватность. В целом, если модель является адекватной, если полученные остатки не могут использоваться для уточнения модели. Иначе говоря, остатки должны быть случайными. 1. Отдельные остаточные автокорреляции rk(e) должны быть малыми. 2. Поведение функции остаточной автокорреляции в целом должно соответствовать автокорреляции, полученным для набора случайных ошибок. 3. Полезно проанализировать временной график остатков, гистограмму остатков, и график их нормального распределения и т. п. Общая проверка адекватности модели проводится с помощью теста Бокса. Льюинга. Этот тест оценивает общие размеры остаточных коэффициентов корреляции.

Этап 4. Прогнозирование на основе выбранной модели 1. Когда адекватная модель найдена, можно делать прогнозы на один или несколько периодов вперед 2. Как только станут доступны данные новых наблюдений, ту же модель ARMA можно применять для модифицированного прогноза, с иным началом отсчета времени. 3. Если характер поведения ряда меняется, новые данные могут послужить для переоценки параметров модели, или, возможно, разработки совершенно новой модели.

Тест Бокса-Льюинга Тестовая статистика имеет вид: и подчиняется приблизительно Хи-квадрат распределению с n-p-q степенями свободы, rk(e) – коэффициент остаточной автокорреляции для лага k; T – число остатков (длина временного ряда); m – количество интервалов временных интервалов, включаемых в проверку. Если наблюдаемое значение Q – статистики превосходит критическое, то рассматриваемая модель неадекватна.

Нестационарные временные ряды: модели ARIMA Многие временные ряды являются нестационарными. Часто нестационарные ряды можно преобразовать в стационарные путем взятия разностей. Предположим временной ряд Yt возрастает со временем, но его первые разности Yt = Yt – Yt-1 изменяется в окрестностях некоторого фиксированного уровня, то есть является стационарным. В этом случае, переходят к первым разностям и для них строят ARMA модель. В некоторых случаях, для того чтобы получить стационарные данные, необходимо взять разностей: 2 Yt = Yt – Yt-1= (Yt – Yt-1) - (Yt-1 – Yt-2) = Yt – 2 Yt-1 + Yt-2 В общем случае число повторных взятий разностей обозначают буквой d.

Модели для нестационарных временных рядов называют моделями авторегрессии интегрированного скользящего среднего ARIMA(p, d, q). Параметр p соответствует порядку авторегрессионной части модели, d определяет порядок разности, q указывает порядок компоненты скользящего среднего. Если исходный ряд является стационарным (d=0), модель ARIMA упрощается до модели ARMA. Несмотря на то, что в моделях ARIMA фигурируют разности, из подобранных моделей всегда может быть сделать прогноз для исходных временных рядов.

Критерии выбора модели Модели ARIMA подбираются на основе предварительного анализа графиков ACF и PACF, идентификации коэффициентов и анализа остатков. Однако в этой процедуре присутствует некоторая доля субъективизма. Возможно, что две или более моделей адекватно описывают данные. Если модели содержат одинаковое число параметров, то обычно предпочтение отдают модели с меньшей среднеквадратической ошибкой s 2. Если модели разное число параметров, то необходимо выбирать между простотой и точностью модели. Согласно критерию Акаике (Akaike) выбирают модель, которая минимизирует выражение: где ln s 2– натуральный логарифм остаточной дисперсии s 2, T – число наблюдений, r – число параметров модели (r=p+q+1).

Согласно Байесовскому критерию, разработанному Шварцем (Schwarz), отбирается та модель, которая минимизирует следующее выражение: Второе слагаемое в формулах критериев AIC и BIC - это штрафной фактор, учитывающий включение в модель дополнительных параметров. Критерий BIC накладывает большее ограничение на количество параметров в сравнении с критерием AIC. Поэтому минимизация критерия BIC всегда даст количество параметров, не превышающее количество, устанавливаемых, согласно критерию AIC. Часто оба критерия дают один и тот же результат. Критерии AIC и BIC следует рассматривать как дополнительные параметры, призванные помочь при окончательном выборе модели. Они не способны заменить внимательное изучение выборочных коэффициентов автокорреляции и частной автокорреляции.

Преимущества и недостатки моделей ARIMA Подход Бокса-Дженкинса к анализу временных рядов является весьма мощным инструментом для построения точных прогнозов с малой дальностью прогнозирования. Модели ARIMA достаточно гибкие и могут описывать широкий спектр характеристик временных рядов, встречающихся на практике. Формальная процедура проверки модели на адекватность проста и доступна. Кроме того, прогнозы и интервалы предсказания следуют непосредственно из подобранной модели. Однако использование моделей ARIMA имеет и несколько недостатков. 1. Необходимо относительно большое количество исходных данных. Следует понимать, что если данные периодичны со, скажем, сезонным периодом S= 12, то наблюдения за один полный год будут составлять фактически одно сезонное значение данных (один взгляд на сезонную структуру), а не двенадцать значений. Вообще говоря, при использовании модели ARIMA для несезонных данных необходимо около 40 или более наблюдений. При построении модели ARIMA для сезонных данных нужны наблюдения приблизительно за 6 -10 лет, в зависимости от величины периода сезонности. 2. Не существует простого способа корректировки параметров моделей ARIMA, такого как в некоторых сглаживающих методах, когда задействуются новые данные. Модель приходится периодически полностью перестраивать, а иногда требуется выбрать совершенно новую модель. 3. Построение удовлетворительной модели ARIMA зачастую требует больших затрат времени и ресурсов. Для моделей ARIMA расходы на построение модели, время выполнения вычислений и объемы необходимых баз данных могут оказаться существенно выше, чем для более традиционных методов прогнозирования, таких как сглаживание.