Модель_кат_теор.ppt
- Количество слайдов: 11
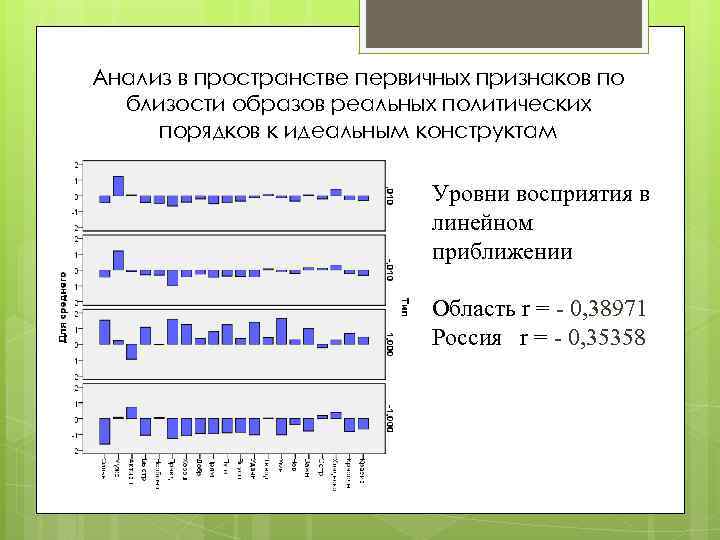
Анализ в пространстве первичных признаков по близости образов реальных политических порядков к идеальным конструктам Уровни восприятия в линейном приближении Область r = - 0, 38971 Россия r = - 0, 35358
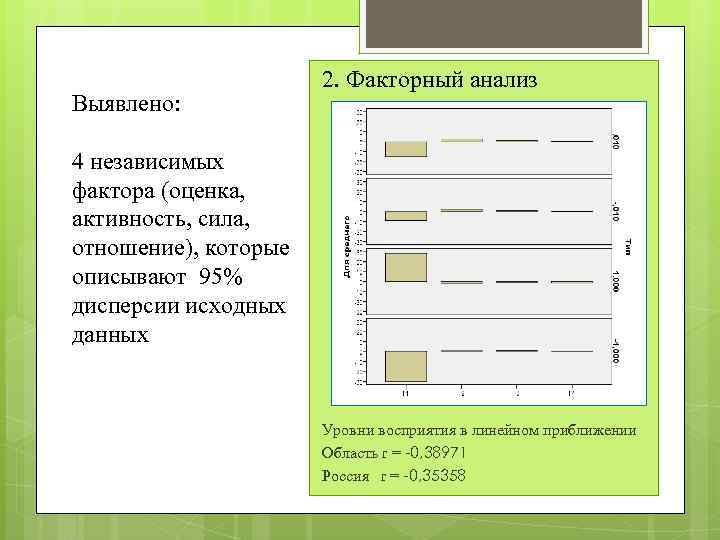
Выявлено: 2. Факторный анализ 4 независимых фактора (оценка, активность, сила, отношение), которые описывают 95% дисперсии исходных данных Уровни восприятия в линейном приближении Область r = -0, 38971 Россия r = -0, 35358

v. Результаты расчетов в линейном приближении по усредненным семантическим портретов: уровень равен rобл = - 0, 35239 для восприятия политического порядка в области и r. Рос = - 0, 31828 для восприятия порядка в России в целом. v. Выявлено 4 латентных фактора, определяющие всю совокупность первичных признаков. Первый фактор описывает 79 % дисперсии всей совокупности результатов. Суммарная дисперсия, соответствующая следующим трем факторам составляет 16 %. Кумулятивная дисперсия, соответствующая этим четырем факторам равна 95 %. v Результаты по линейному приближения в факторном пространстве: уровень равен rобл = - 0, 38971 для восприятия политического порядка в области и r. Рос = - 0, 35358 для восприятия порядка в России в целом

Линейное приближение Близость образов двух объектов в семантическом пространстве оценивается по абсолютным и относительным расстояниям между образами. Абсолютное расстояние между образами k и l рассчитывается по обычной формуле ( где xki и xli – координаты точек в пространстве признаков, N=20 – размерность этого пространства, k и l – тип политического порядка). Для анализа удобнее пользоваться относительным расстоянием между образами. При нормировке расстояния между образами двух идеальных порядков на 2, формулы расчета относительного расстояния dkl выглядят следующим образом: В соответствии с теорий идеальной точки Кумбса, уровень эмоционального восприятия определяется относительными расстояниями
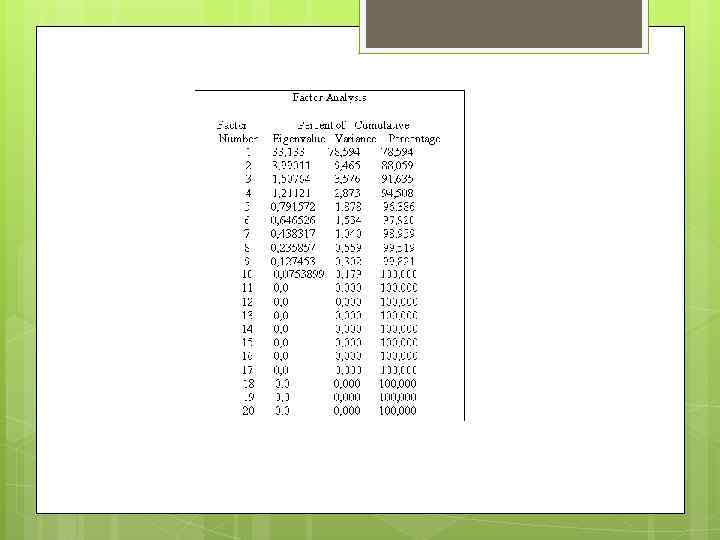

Уровень достоверности линейного приближения: ≈ 0, 8 Для повышения уровня до 0, 95 необходимо учитывать все 4 фактора и строить нелинейное приближение. Модель в рамках теории катастроф Психосемантическая феноменологическая модель Изменение уровня восприятия r' описывается градиентным образом dr'/dt=-d. F/dr', где F – некоторая функция общего положения (потенциал эмоционального восприятия) Уравнение стационарного состояния: d. F/dr‘=0

Результаты модели не всегда корелируют Для более адекватной привязки моделей было предложено выйти за пределы классического метода семантического дифференциала. Использовать для уменьшения размерности исходных данных (первичных семантических признаков) не только корреляции между ними (факторный анализ), но и особенности восприятия респондентов. Многомерное шкалирование, который также как и факторный анализ уменьшает размерность переменных, но кроме того, позволяет учесть особенности восприятия исследуемого процесса, и опирается на модель идеальной точки Кумбса.
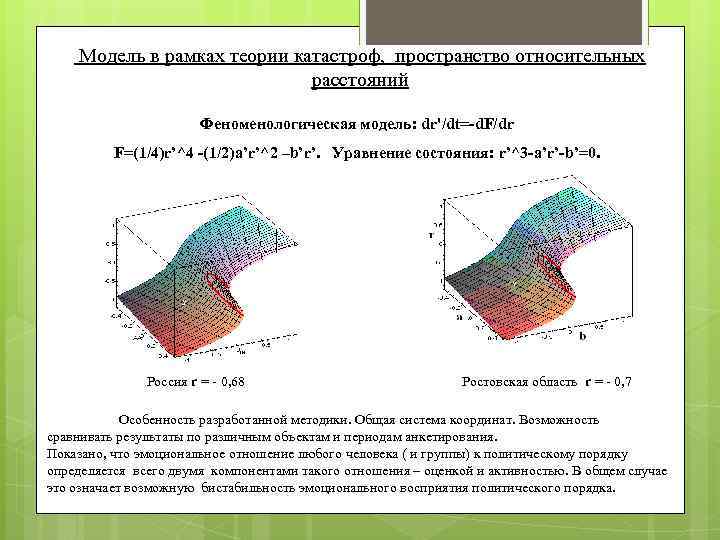
Модель в рамках теории катастроф, пространство относительных расстояний Феноменологическая модель: dr'/dt=-d. F/dr F=(1/4)r’^4 -(1/2)a’r’^2 –b’r’. Уравнение состояния: r’^3 -a’r’-b’=0. Россия r = - 0, 68 Ростовская область r = - 0, 7 Особенность разработанной методики. Общая система координат. Возможность сравнивать результаты по различным объектам и периодам анкетирования. Показано, что эмоциональное отношение любого человека ( и группы) к политическому порядку определяется всего двумя компонентами такого отношения – оценкой и активностью. В общем случае это означает возможную бистабильность эмоционального восприятия политического порядка.

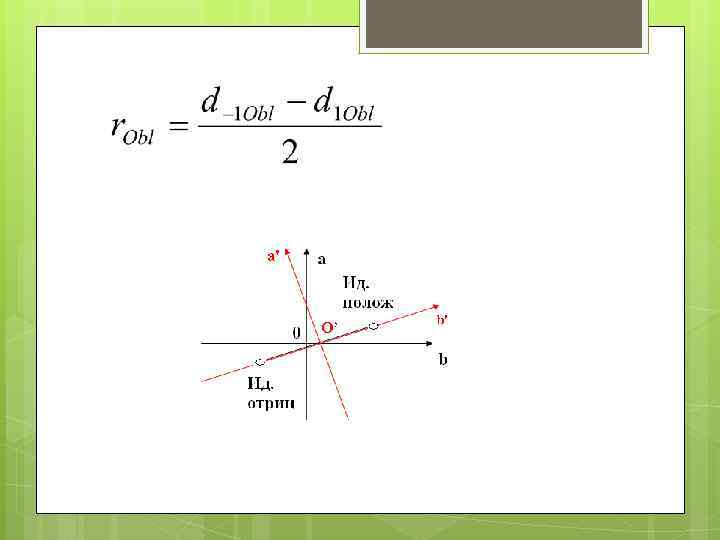
a и b – феноменологические параметры, диффеморфно зависящие от относительных расстояний d 1 x и d -1 x, где x означает Obl или Ros соответственно , модельный параметр порядка r’ также диффеоморфен уровню эмоционального восприятия r. Для определения явного вида этой зависимости рассмотрим группу перестановок образов идеальных конструктов. a= -(d 1 x + d -1 x)/2; b= (d -1 x - d 1 x)/2. Здесь

Модель в рамках теории катастроф Психосемантическая феноменологическая модель Изменение уровня восприятия r' описывается градиентным образом dr'/dt=-d. F/dr', где F – некоторая функция общего положения (потенциал эмоционального восприятия) Уравнение стационарного состояния: d. F/dr‘=0 F=(1/4)r’ 4 -(1/2)a’r’ 2 –b’r’. Уравнение состояния: r’ 3 -a’r’-b’=0. a= -(d 1 x + d -1 x)/2; b= (d -1 x - d 1 x)/2. r’=β r, β находится из условий нормировки.
Модель_кат_теор.ppt