Анализ результатов определений о чем говорят нам результаты

Анализ результатов определений (о чем говорят нам результаты наших инструментальных методов определения различных веществ)

В прошлый раз мы говорили о градуировочной функции. Мы допускали, что Градуировочная функция линейна и определяли её параметры — тангенс угла наклона к оси абсцисс и пересечение с осью ординат. И говорили о том, что результаты определения вещества в градуировочных растворах никогда не лягут точно на нашу градуировочную функцию. И поэтому мы, для определения её параметров, пользуемся методом наименьших квадратов (Ексель, Сервис, анализ данных, регрессия). Но это только начало. Когда мы начинаем определять наше вещество, для которого мы построили градуировочную функцию, в реальной пробе (нитраты в огурцах, например), мы каждый раз получаем разные результаты. Например, такие

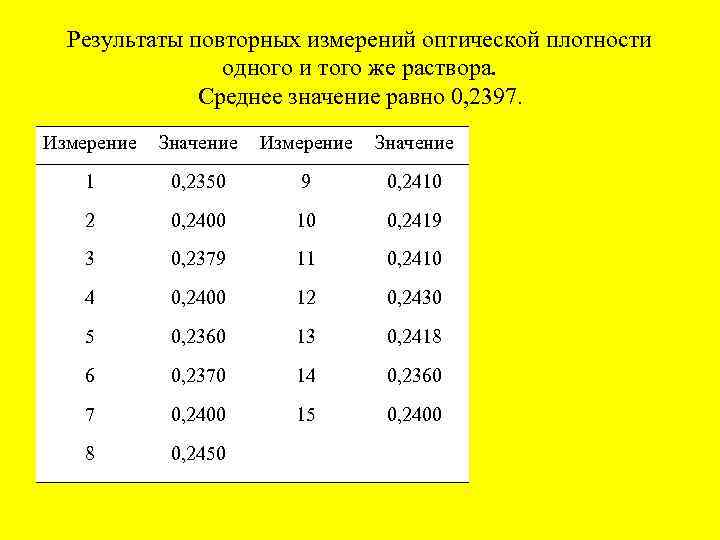Результаты повторных измерений оптической плотности одного и того же раствора. Среднее значение равно 0, 2397. Измерение Значение 1 0, 2350 9 0, 2410 2 0, 2400 10 0, 2419 3 0, 2379 11 0, 2410 4 0, 2400 12 0, 2430 5 0, 2360 13 0, 2418 6 0, 2370 14 0, 2360 7 0, 2400 15 0, 2400 8 0, 2450

Очень часто это приводит к таким результатам: В пробе сточной воды три раза определяли содержание фенола. Найденное среднее значение равно 0. 51 мг/л ПДК (предельно допустимая концентрация) фенола в сточных водах равна 0. 5 мг/л. Что значит ПДК для сточных вод? А это значит, что сточные воды сливают в канализационные трубы, из которых она поступает на станцию очистки. При превышении установленных нормативов в поступающих на очистку сточных водах очистные сооружения (как правило, аэротенки, где происходит биологическая очистка) могут выйти из строя. Это катастрофа! Что делать? Можно сливать такую воду в канализацию или нет? (Счет за выход из строя аэротенков будет астрономический) Как правильно интерпретировать результаты анализа?

Это не для вас? Увы! Очень часто при анализе остаточных содержаний пестицидов в продуктах вы будете попадать в такую же ситуацию. Пустить в продажу продукты с превышением ПДК — уголовное преступление. Но не пустить в продажу продукты с содержанием пестицидов не более ПДК — большие финансовые потери. Как быть? При определении нефтепродуктов в бутилированной питьевой воде — а ПДК нефтепродуктов в этой воде от 0, 01 (вода высшей категории) до 0, 05 мг/л (вода первой категории)— вы часто будете получать 0, 02 или 0, 07 мг/л. Как быть? Принимать такую партию воды или нет? И с другими продуктами очень часто будет точно такая же история. Так как же интерпретировать результаты определения?

Понятие о случайной величине И потому нам надо вспомнить о случайных величинах. Как вы, вероятно, знаете, на свете нет двух одинаковых вещей. Даже два шарика от шарикоподшипника будут разными (http: //roller. ru/content/kolesa/article-24. html). Они немножко отличаются по размеру. А к шарикам предъявляют очень высокие требования. Происходит это самых разных причин. От того, что ветерок подул в цехе (температура изменилась), от того, что напряжение в электрической сети немного изменилось, от того, что машина рядом с цехом проехала и стены и пол задрожали и от множества других случайных причин, которые мы учесть не в силах. Но именно потому, что причин этих много, в действии их на конечный результат прослеживается определенная закономерность.

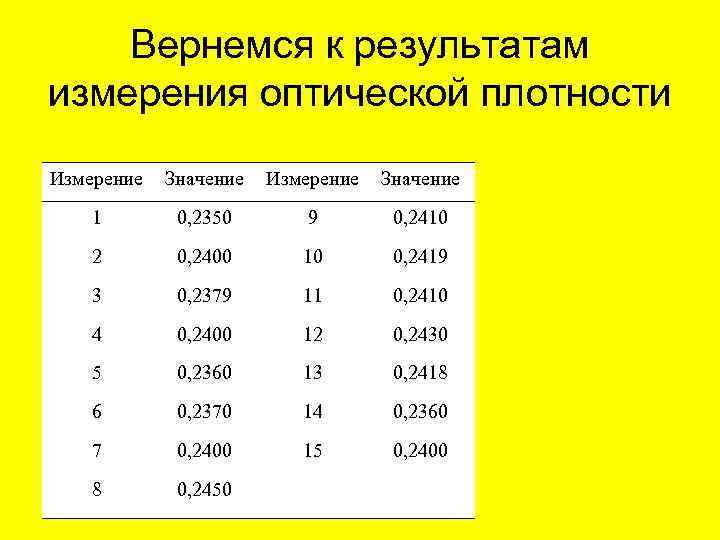Вернемся к результатам измерения оптической плотности Измерение Значение 1 0, 2350 9 0, 2410 2 0, 2400 10 0, 2419 3 0, 2379 11 0, 2410 4 0, 2400 12 0, 2430 5 0, 2360 13 0, 2418 6 0, 2370 14 0, 2360 7 0, 2400 15 0, 2400 8 0, 2450

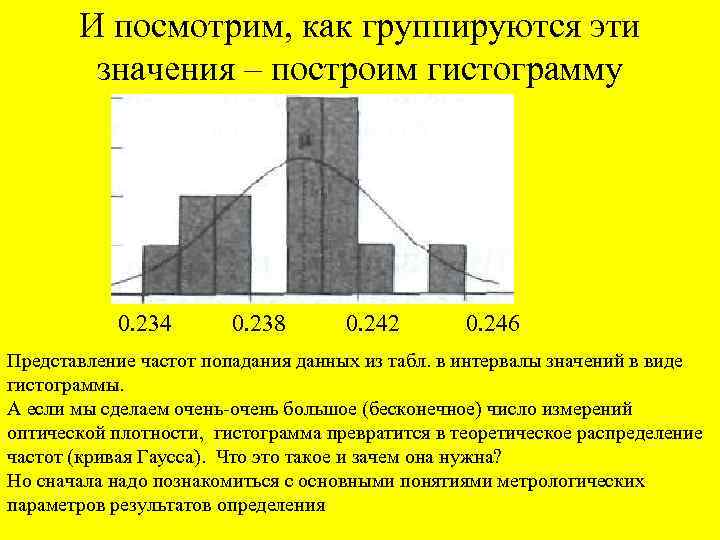И посмотрим, как группируются эти значения – построим гистограмму 0. 234 0. 238 0. 242 0. 246 Представление частот попадания данных из табл. в интервалы значений в виде гистограммы. А если мы сделаем очень-очень большое (бесконечное) число измерений оптической плотности, гистограмма превратится в теоретическое распределение частот (кривая Гаусса). Что это такое и зачем она нужна? Но сначала надо познакомиться с основными понятиями метрологических параметров результатов определения

Погрешности анализа бывают случайные и систематические. Если мы, например, градуировку делали, используя одну кювету, а для определения используем кювету, которая немного толще или тоньше (с отечественными кюветами это случалось), то это будет вносить систематическую ошибку. Систематические ошибки «сдвигают» результат определения в одну сторону. А при случайных погрешностях результаты определения при их повторении случайным образом разбросаны относительно друга. Величину случайной погрешности определения характеризует понятие «воспроизводимость» результатов определения. Оценивают её, выполнив независимую серию повторных (параллельных) определений и рассчитав величину стандартного отклонения результатов относительно среднего значения.

Все мы знакомы с понятием средней величины. Если у нас n параллельных определений, то средняя величина Стандартное отклонение можно выразить и в относительной форме, разделив его на среднее значение. Относительное стандартное отклонение sr вычисляется как sr=sy/yср

Общая погрешность процесса анализа определяется не только погрешностью измерения соответствующим образом подготовленной пробы, но и погрешностями пробоотбора, пробоподготовки и обработки данных. Для оценки общей погрешности служит закон распространения погрешностей. При наличии нескольких суммирующихся независимых друг от друга источников погрешностей для оценки общей погрешности следует сложить квадраты стандартных отклонений — дисперсии — отдельных составляющих. Для оценки погрешности произведения или частного следует сложить квадраты относительных случайных погрешностей. Однако при всех этих операциях мы оцениваем «воспроизводимость» , а не правильность определения. Может случиться так, что воспроизводимость результатов определения очень хорошая, но определяем мы плохо. И это серьезная проблема. Для характеристики правильности результатов определения служит «процентная мера правильности» (recovery =100 Хср/Хист). Определить эту величину очень сложно (определяют сравнением результатов определения разными методами и разными лабораториями)

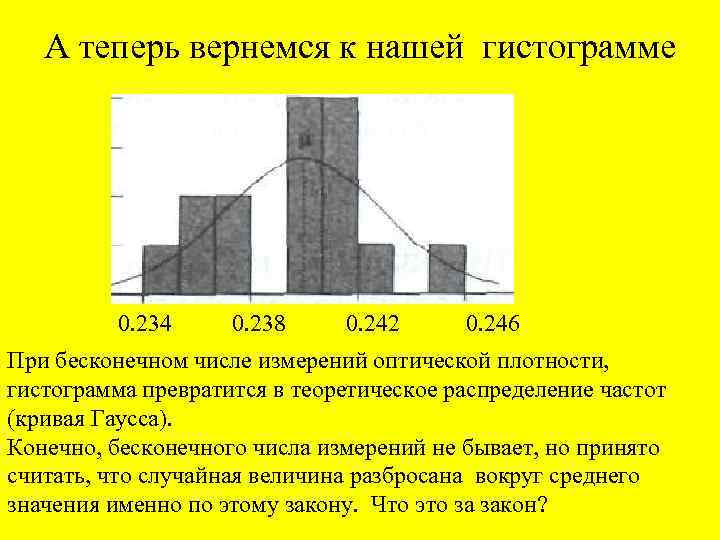А теперь вернемся к нашей гистограмме 0. 234 0. 238 0. 242 0. 246 При бесконечном числе измерений оптической плотности, гистограмма превратится в теоретическое распределение частот (кривая Гаусса). Конечно, бесконечного числа измерений не бывает, но принято считать, что случайная величина разбросана вокруг среднего значения именно по этому закону. Что это за закон?

Случайная величина при бесконечном числе определений Характеристики случайной величины Математическим ожиданием М (Х) дискретной случайной величины Х называется сумма произведений всех возможных значений величины Х на соответствующие вероятности: М(Х) = x 1· p 1 + x 2· p 2 + … + xn· pn. Грубо говоря, среднее значение Дисперсией D (X) дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания: D(X) = M [(X - M(X))2] или D(X) = M (X 2) - M 2(X). Грубо говоря, квадрат стандартного отклонения Средним квадратическим отклонением s(Х) случайной величины Х называется корень квадратный из ее дисперсии: Интегральной функцией распределения непрерывной случайной величины Х называется функция F(x), равная вероятности того, что Х приняла значение, меньшее х: F(x) = P(X < x). Дифференциальной функцией распределения непрерывной случайной величины Х (или ее плотностью вероятности) называется функция f(x), равная производной интегральной функции:

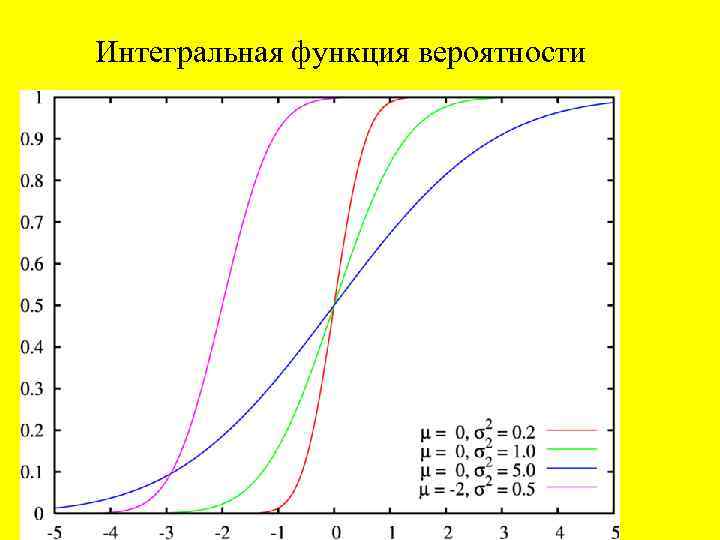Интегральная функция вероятности

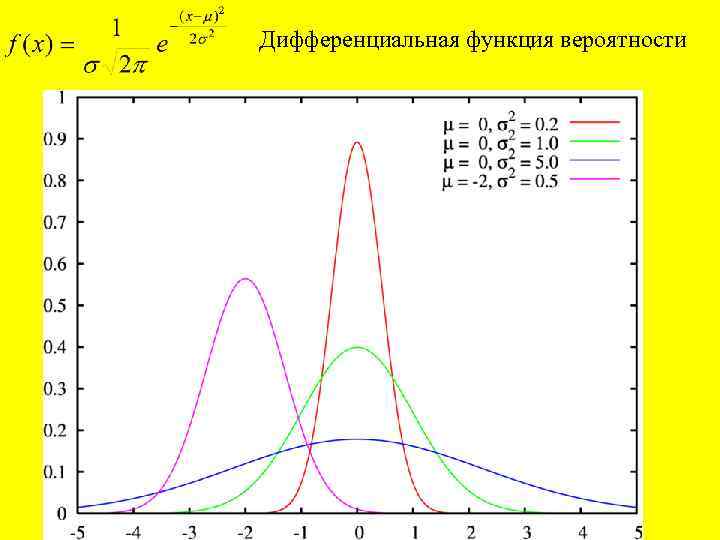Дифференциальная функция вероятности

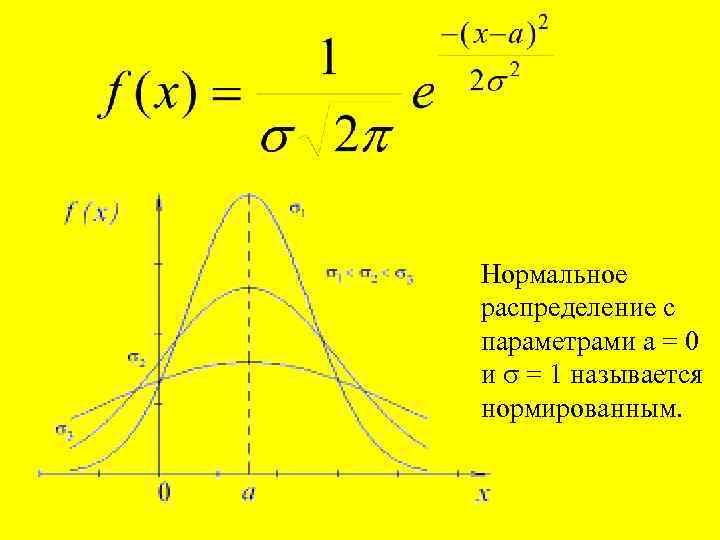Нормальное распределение с параметрами а = 0 и = 1 называется нормированным.

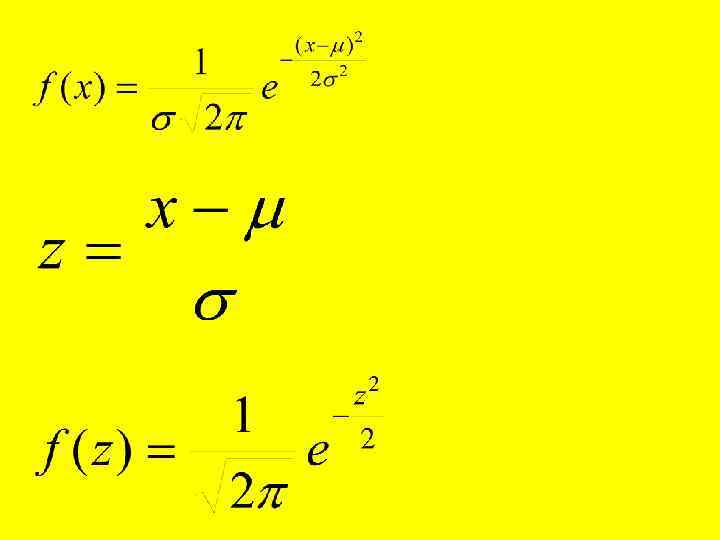
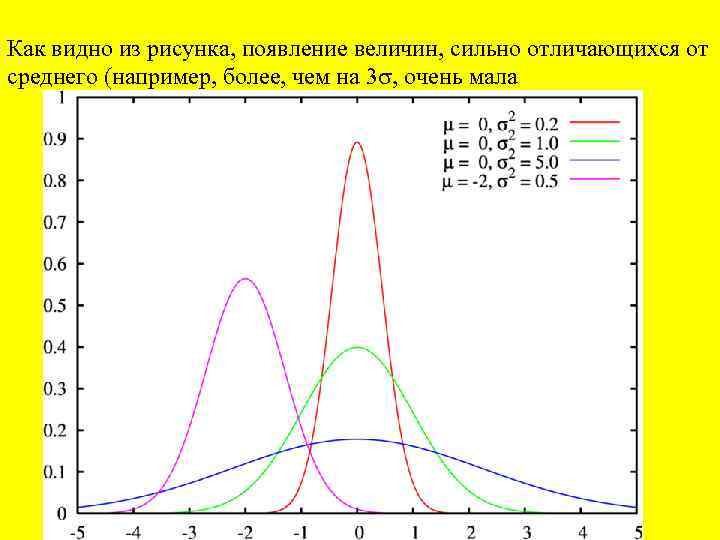Как видно из рисунка, появление величин, сильно отличающихся от среднего (например, более, чем на 3 , очень мала

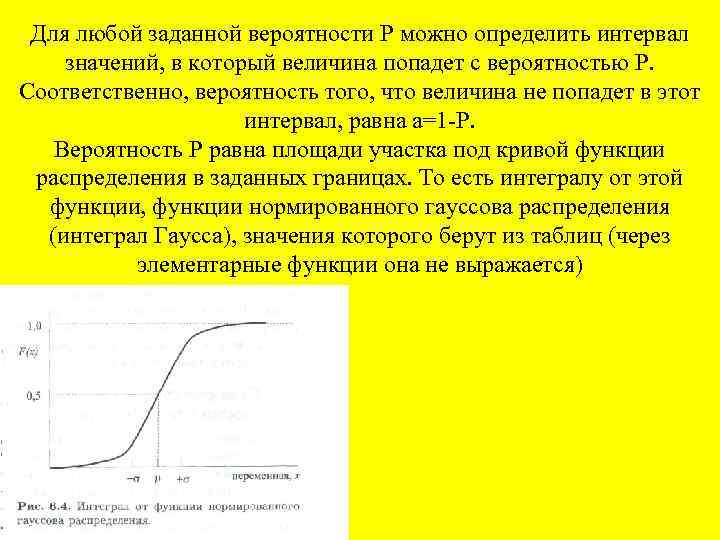Для любой заданной вероятности Р можно определить интервал значений, в который величина попадет с вероятностью Р. Соответственно, вероятность того, что величина не попадет в этот интервал, равна а=1 -Р. Вероятность Р равна площади участка под кривой функции распределения в заданных границах. То есть интегралу от этой функции, функции нормированного гауссова распределения (интеграл Гаусса), значения которого берут из таблиц (через элементарные функции она не выражается)

Пример. Какова вероятность того, что результат измерения окажется между значениями 27, 5 и 37, 5. если среднее значение равно =25, 0 а дисперсия равна 2=25, 0 Для нормированного распределения z=(x- )/ То есть Z 1=(27. 5 -25. 0)/sqr(25)=0. 5 Z 2=(37. 5 -25. 0)/sqr(25. 0)=2. 5 Значения интеграла Гаусса равны, соответственно, 0, 99379 и 0, 69146 То есть искомая вероятность равна 0, 99379 - 0, 69146= 0, 30233 или 30, 23%

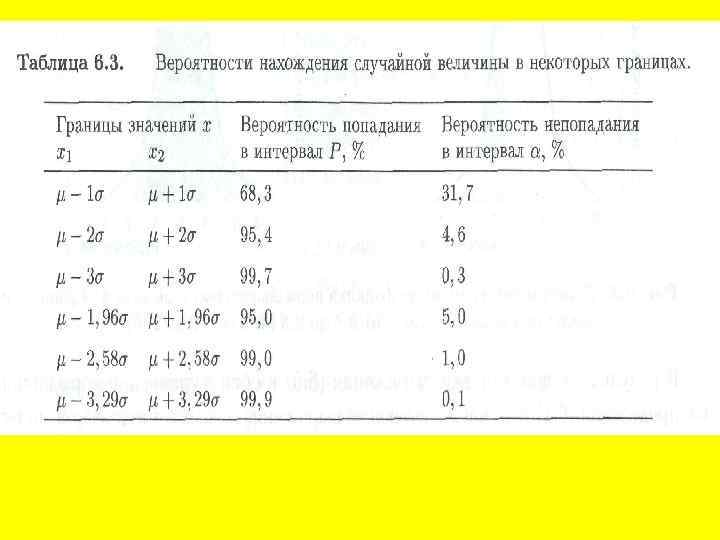
В химическом анализе для проверки результатов чаще всего используют значения Р, равные 0, 95 или 0, 99. Еще раз отметим, что распределение Гаусса строго применимо лишь для описания бесконечно большой серии данных, для которой величины и известны точно. Но такого не бывает. Если же известны лишь их приближенные оценки х и s, то для расчета вероятностей и соответствующих им границ значений вместо распределения Гаусса следует использовать распределение Стьюдента (t-распределение). Оно очень часто используется в различных статистических тестах. И вообще. В статистике ничего строго рассчитать нельзя. Можно только «оценить» . И вот теперь мы вернемся к самому началу. Когда у нас есть реальная задача и небольшое число измерений.

Распределение Стьюдента — это, так сказать, исправленное распределение Гаусса. Которое учитывает, что число измерений у нас ограничено. И потому наши оценки погрешности будут отличаться от «теоретических» . Естественно, в этом случае оценки будут грубее, но с этим приходится смириться — бесконечного число измерений мы сделать не можем. Однако при использовании этого распределения мы предполагаем, что распределение случайной величины подчиняется распределению Гаусса. Как вы помните, задача была такая: В пробе сточной воды три раза определяли содержание фенола. Найденное среднее значение равно 0. 51 мг/л ПДК (предельно допустимая концентрация) фенола в сточных водах равна 0. 5 мг/л. Нам нужно определить, превышена или нет ПДК.

Предположим, что величины 0, 50( ) и 0, 51(Хср) — это одна и та же величина, а различие между ними чисто случайно. Это НУЛЬГИПОТЕЗА Альтернативная гипотеза — что это разные величины. Простой t-тест Стьюдента для проверки гипотезы о различии между средним значением и начинается с вычисления Тестовой статистики T=[X- ]sqr(n)/S Где S — оценка стандартного отклонения той серии данных, из которых рассчитана величина X (среднее значение) n — число измерений в серии Затем выбирают уровень значимости альтернативной теории — достаточно малую вероятность принять эту теорию. Обычно это 0, 05 или 0, 01 (для Р=0, 95 и Р=0, 99) По таблице находят критическое значение функции распределения при степени свободы f=n-1 Если рассчитанное значение не превышает табличного, принимают нуль-гипотезу, в противном случае — альтернативную.

Пример Три определения Среднее значение 0, 513 мг/л, стандартное отклонение 0, 05 мг/л Аттестованное значение равно 0, 52 мг/л. Можно ли утверждать, что погрешность имеет случайный характер? Нуль-гипотеза — да Альтернативная — нет T=[0. 513 -0. 52]sqr(3)/0. 05=0. 242 Из таблиц для двухстороннего теста t(a=5%, f=2)=4. 0303 То есть различие случайно, величины одинаковы. В этом случае нас интересовало, есть ли различие. И потому тест двухсторонний. А если нас интересует, превышает ли экспериментальная величина заданное значение, применяют односторонний тест t=[0. 513 -0. 5]sqr(3)/0. 05=0. 45 При t(a=5%, f=2)=2. 902 Это меньше критического. Значение ПДК не превышено

Не пугайтесь. Запомнить вы это не запомните, но помнить, что вы это слышали вам надо. И посмотрите в Сети, что такое карты Шухарта