06 временной метод_.ppt
- Количество слайдов: 8

АНАЛИЗ ДИНАМИЧЕСКИХ ЦЕПЕЙ ВО ВРЕМЕННОЙ ОБЛАСТИ ПРИ ВОЗДЕЙСТВИИ СИГНАЛОВ ПРОИЗВОЛЬНОЙ ФОРМЫ

Метод наложения позволяет разложить заданное входное воздействие сложной формы на подобные другу слагаемые более простой формы, для которых легко найти реакцию цепи. Суммируя эти реакции, можно определить реакцию цепи на сложное воздействие. Отдельные составляющие целесообразно выбирать так, чтобы они были математически простыми, и расчет реакций, ими вызываемых, был бы несложен. Элементарные составляющие воздействия выражают с помощью двух функций: 1. Единичная функция (единичного скачка); 2. Импульсной функцией (дельта-функция). Единичная функция. С помощью единичной функции любая функция времени может быть представлена в виде произведения. Например, U=ƒ(t) *1(t). Если воздействие подается на цепь не в момент t=0, а с запаздыванием на t 1, его следует записать с помощью единичной функции с запаздывающим аргументом. Реакция цепи на единичную функцию называется переходной характеристикой цепи и обозначается h(t) определяется при нулевых начальных условиях. В зависимости от типа реакции и типа воздействия (ток или напряжение)переходная характеристика может быть безразмерной величиной, либо иметь размерность А/В или В/А. h(t) можно находить как классически, так и операторными методами.

Интеграл Дюамеля. Требуется определить ток в линейном пассивном двухполюснике, переходная характеристика которого известна. Начальный запас энергии двухполюсника равен нулю. Hy(t)= i(t)/1(t). Текущее время обозначим через τ, изменяется в пределах 0≤τ≤t. Замена плавной кривой ступенчатой позволяет считать, что в момент времени τ=0 включается постоянное начальное напряжение U(0)*1(τ) воздействующее на цепь в течении всего интервала времени от нуля до ∞. Затем, через промежуток времени τ1 вступает в действие дополнительное постоянное напряжение величиной ∆U 1, воздействующее на цепь начиная с момента времени τ1 и т. д. Используя единичную функцию времени с запаздывающим аргументом, можно приближенно записать приложенное к цепи напряжение в виде суммы: Реакция цепи (ток) определяется как алгебраическая сумма реакций цепи на воздействия начального напряжения и всех последующих скачков напряжения, включаемых друг за другом. n- число промежутков, на которое разбит интервал времени от 0 до t.

Для того, чтобы перейти от ступенчатой кривой напряжения к заданному плавно изменяющемуся напряжению, необходимо промежутки времени уменьшить до бесконечно малой величины dτ, а n→∞. Величину каждого скачка d. U можно представить : d. U/dτ=U′(τ) d. U= U′(τ)dτ В пределе сумма перейдет в интеграл: Данное выражение называется интегралом Дюамеля. Интеграл Дюамеля записывают и в других формах. Докажем для двух функций ƒ 1(t) и ƒ 2(t) при t>0 Каждый интегралов в приведенном равенстве называется сверткой функции ƒ 1(t) и ƒ 2(t). Для доказательства справедливости этого равенства проведем подстановку t- τ =x, тогда dτ=-dx и τ=t-x. Пределы изменятся при τ=t, верхних предел х=0, а при τ=о нижний предел х=τ. Под знаком интеграла можно поменять местами и в этом состоит эквивалентное преобразование интеграла вида свертки функции. Вторая форма записи интеграла Дюамеля. Выполнив интегрирование по частям в первой форме записи интеграла Дюамеля, найдем третью форму записи:

Используем вновь эквивалентное преобразование интеграла, получим четвертую форму записи интеграла Дюамеля: Включение пассивного двухполюсника на напряжение (ток) любой формы. Интегралом Дюамеля применим и в тех случаях, когда напряжение, подводимое к цепи, представляет собой кусочно-непрерывную функцию, содержащие разрывы непрерывности первого рода, т. е. скачки напряжения (тока) конечной величины. hy(t) для данной цепи известна. Рассмотрим 2 интервала 0≤t≤t 1. Интеграл Дюамеля данного промежутка времени:

Импульсная функция. Импульсная характеристика. Данный импульс можно сформировать, используя единичную функцию: Интерес в теоретическом отношении представляет предельный случай δ(t, ∆t), когда ∆t→ 0, а высота А→∞ δ(t) называется импульсная функция, часто δ(t) называют «дельта-функцией» или «функцией Дирака» . Импульсная функция обладает следующими свойствами: 1. δ=0 при t<0 и при t>0 δ(t)=0 при t≠ 0 2. δ(0)=∞ 3. Данный импульс является, конечно, математической абстракцией. Импульс можно считать коротким, если его длительность ∆t несоизмеримо мала по сравнению с постоянной времени цепи или периодом собственных колебаний контура. В цепи, на которую воздействует такой импульс, возникает переходный процесс.

Если δ(t) отлична от нуля не в момент t=0, а в момент τ, т. у. запаздывает на время τ, то она записывается с запаздывающим аргументом δ(t- τ). Свойство функции сохраняется. Между импульсной и единичной функцией существует аналитическая связь: Импульсная характеристика. Импульсной характеристикой цепи называют реакцию цепи на воздействие импульсной функции δ(t) , обозначается импульсная характеристика g(t). При рассмотрении линейных цепей, следствия находятся в тех же соотношениях, что и вызывающие их причины, реакция цепи на воздействие импульсной функции должна быть производной реакции цепи на воздействие единичной функции.
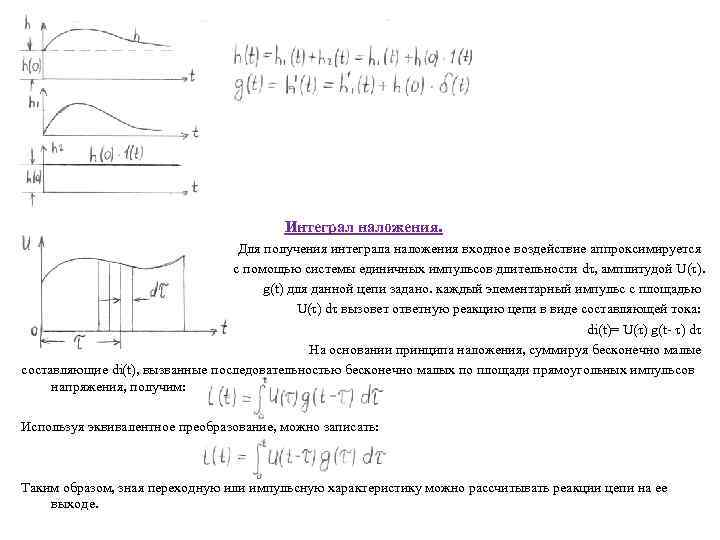
Интеграл наложения. Для получения интеграла наложения входное воздействие аппроксимируется с помощью системы единичных импульсов длительности dτ, амплитудой U(τ). g(t) для данной цепи задано. каждый элементарный импульс с площадью U(τ) dτ вызовет ответную реакцию цепи в виде составляющей тока: di(t)= U(τ) g(t- τ) dτ На основании принципа наложения, суммируя бесконечно малые составляющие di(t), вызванные последовательностью бесконечно малых по площади прямоугольных импульсов напряжения, получим: Используя эквивалентное преобразование, можно записать: Таким образом, зная переходную или импульсную характеристику можно рассчитывать реакции цепи на ее выходе.
06 временной метод_.ppt