Анализ данных в системе Fitter Алексей Померанцев Институт

Анализ данных в системе Fitter Алексей Померанцев Институт химической физики РАН 17. 02. 03 1

Содержание 1. Введение 2. Данные 3. Модель 4. Оценка параметров 5. Пример Box. Bod 6. Прогнозирование 7. Тестирование модели 8. Мультиколлинеарность 9. Прогноз срока службы ПВХ изоляции 10. Выводы 17. 02. 03 2

1. Введение 17. 02. 03 3

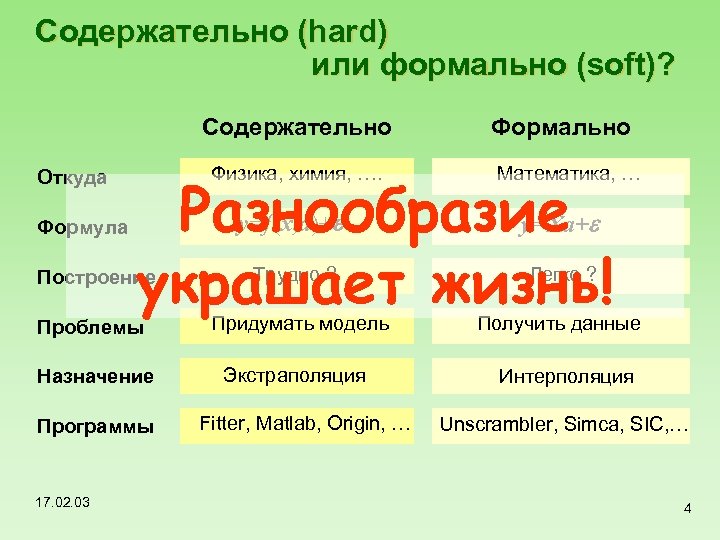Содержательно (hard) или формально (soft)? Содержательно Откуда Формула Физика, химия, …. Формально Математика, … e Разнообразие e украшает жизнь! y=f (x, a)+ y=Xa+ Построение Трудно ? Легко ? Проблемы Придумать модель Получить данные Назначение Экстраполяция Программы 17. 02. 03 Fitter, Matlab, Origin, … Интерполяция Unscrambler, Simca, SIC, … 4

Система Fitter –это надстройка (Add-In) к программе Excel Фактор Отклик Модель 17. 02. 03 Значения Веса Комментарии Параметры Уравнение 5

Установка Fitter Add-In установлен! 17. 02. 03 6

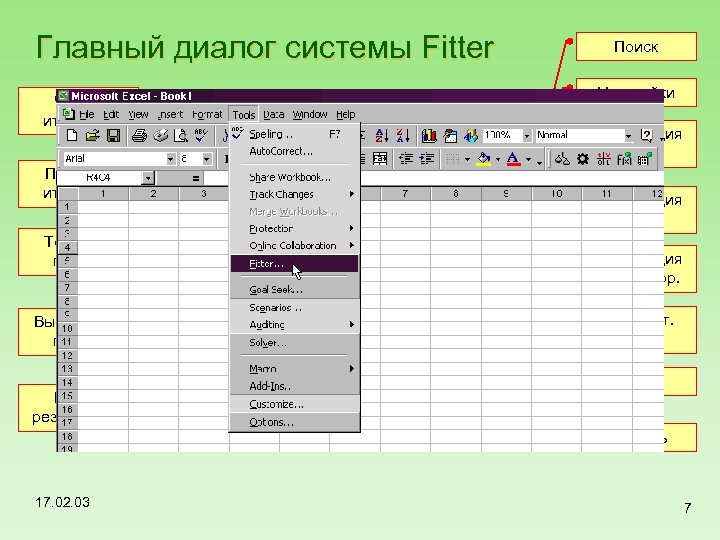Главный диалог системы Fitter Число итераций Пауза на итерации Точность поиска Вывод хода поиска Вывод результатов Поиск Настройки Регистрация данных Регистрация модели Регистрация апр. инфор. Дополнит. диалог Выход Помощь 17. 02. 03 7

2. Данные 17. 02. 03 8

Данные и ошибки При содержательном подходе связь между данными нелинейная например Отклик Предикторы Веса Параметры Модель Вес и дисперсия y=a 1*exp(a 2*x)+a 3*exp(a 4*x) Абсолютная Относительная 17. 02. 03 9

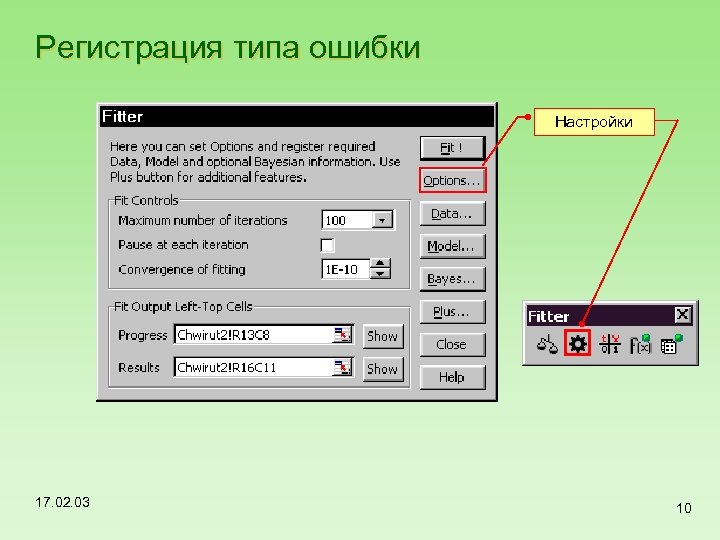Регистрация типа ошибки Настройки 17. 02. 03 10

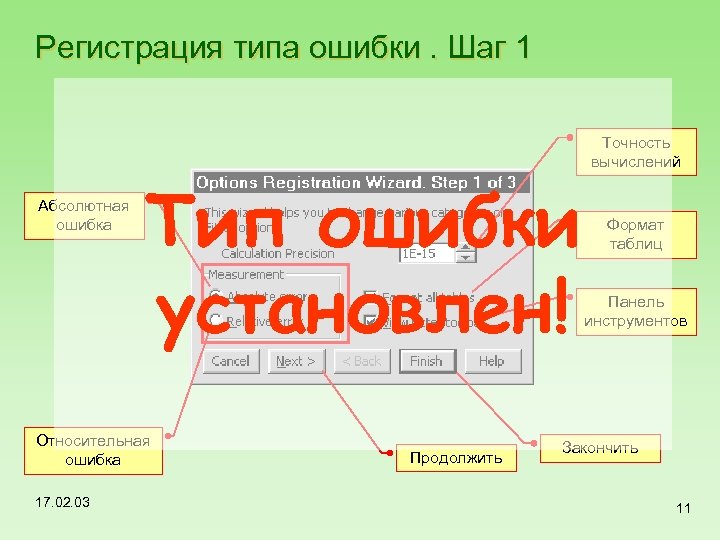Регистрация типа ошибки. Шаг 1 Абсолютная ошибка Тип ошибки установлен! Относительная ошибка 17. 02. 03 Продолжить Точность вычислений Формат таблиц Панель инструментов Закончить 11

Представление данных в системе Fitter Все данные вводятся и выводятся на страницу Excel 17. 02. 03 12

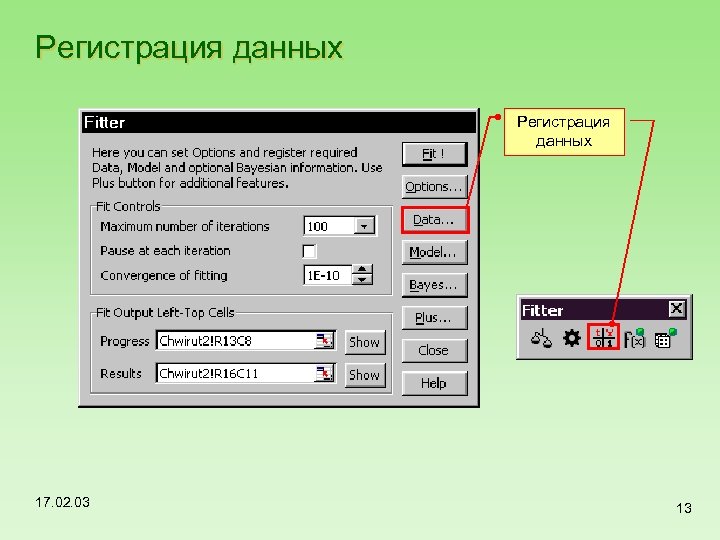Регистрация данных 17. 02. 03 13

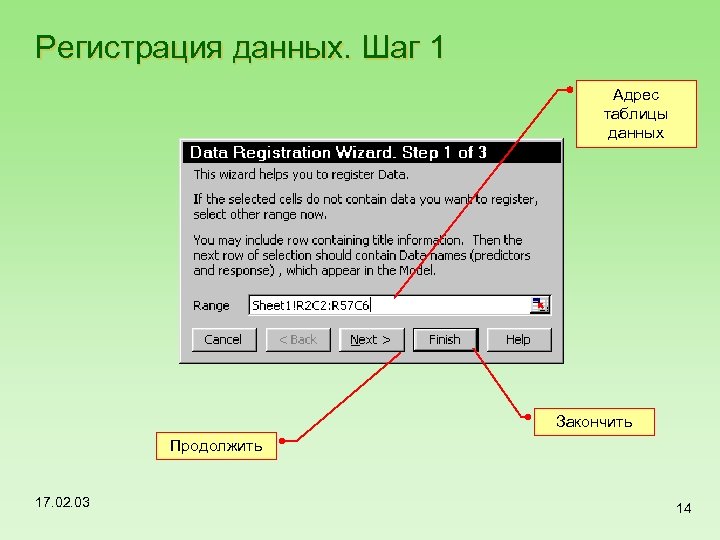Регистрация данных. Шаг 1 Адрес таблицы данных Закончить Продолжить 17. 02. 03 14

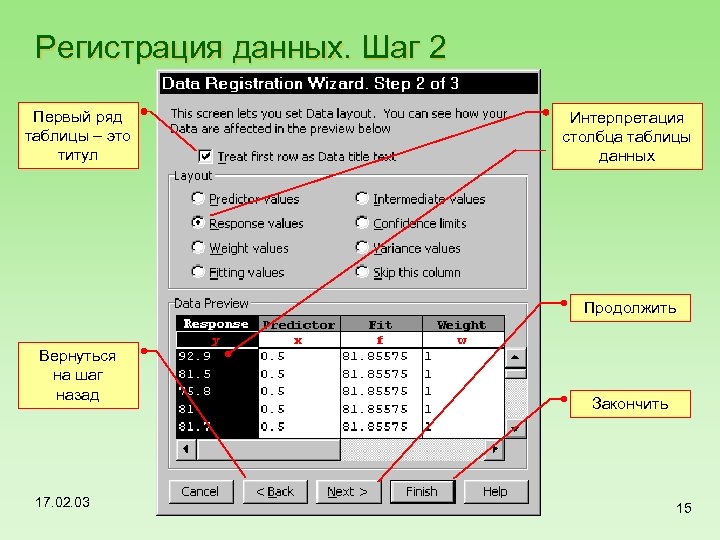Регистрация данных. Шаг 2 Первый ряд таблицы – это титул Интерпретация столбца таблицы данных Продолжить Вернуться на шаг назад 17. 02. 03 Закончить 15

Регистрация данных. Шаг 3 При регистрации данные нельзя изменить, а можно только объяснять Результаты регистрации таблицы данных Вернуться на шаг назад 17. 02. 03 Закончить 16

3. Модель 17. 02. 03 17

Данные и модель Мера согласия данных и моделиэто сумма квадратов отклонений Мера согласия 17. 02. 03 18

Представление модели в системе Fitter Модель записывается в текстовое поле (Text Box), а параметры на страницу Excel 17. 02. 03 19

Модель f(x, a) Различные формы записи одной и той же модели y = a + (b – a)*exp(–c*x) Явная Очень сложная модель! 0 = a + (b – a)*exp(–c*x) – y Неявная Дифф. уравнение d[y]/d[x] = – c*(y –a); y(0) = b Представление в Fitter 17. 02. 03 20

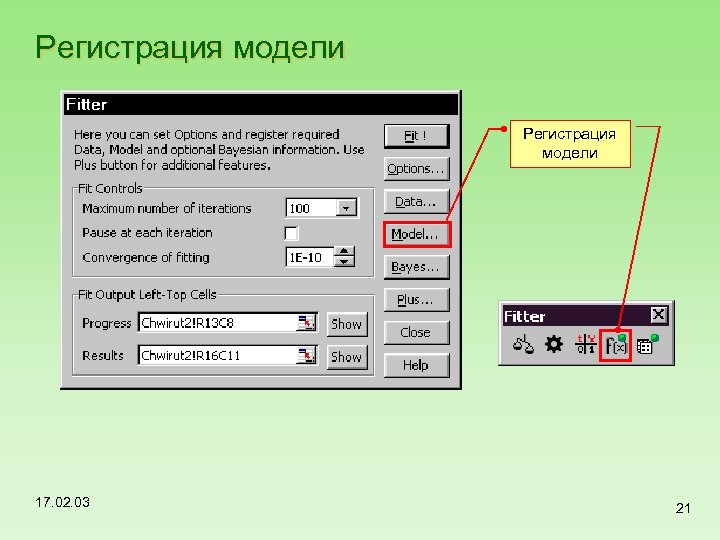Регистрация модели 17. 02. 03 21

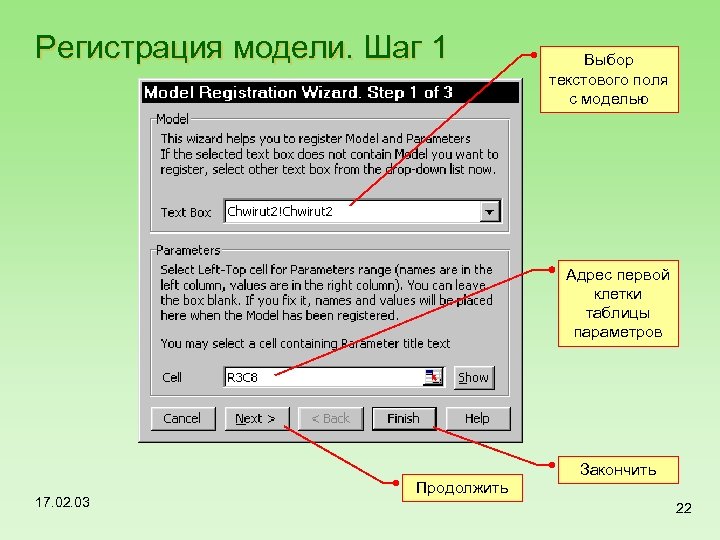Регистрация модели. Шаг 1 Выбор текстового поля с моделью Адрес первой клетки таблицы параметров Закончить 17. 02. 03 Продолжить 22

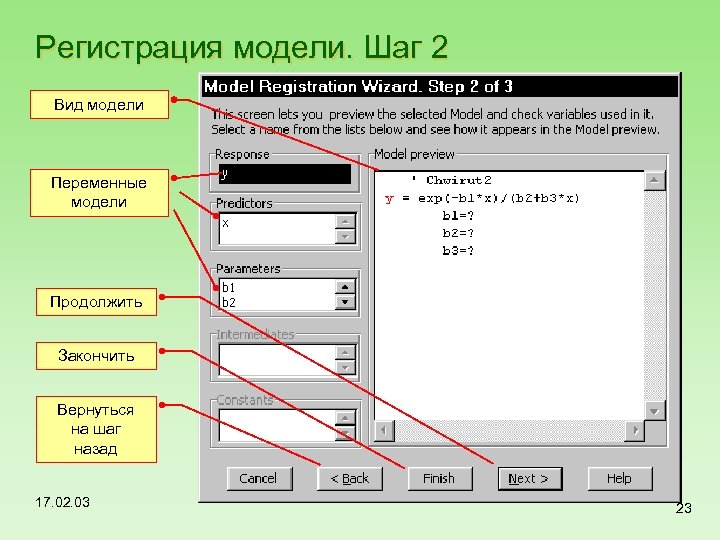Регистрация модели. Шаг 2 Вид модели Переменные модели Продолжить Закончить Вернуться на шаг назад 17. 02. 03 23

Регистрация модели. Шаг 3 При регистрации модель нельзя изменить, а можно только объяснять Первый ряд таблицы параметров – это титул Вернуться на шаг назад 17. 02. 03 Начальные значения параметров Закончить 24

4. Оценка параметров 17. 02. 03 25

Целевая функция Q(a) Целевая функция Qэто сумма квадратов и, может быть, что-то еще… Сумма квадратов Байесовский член Целевая функция Оценки параметров 17. 02. 03 26

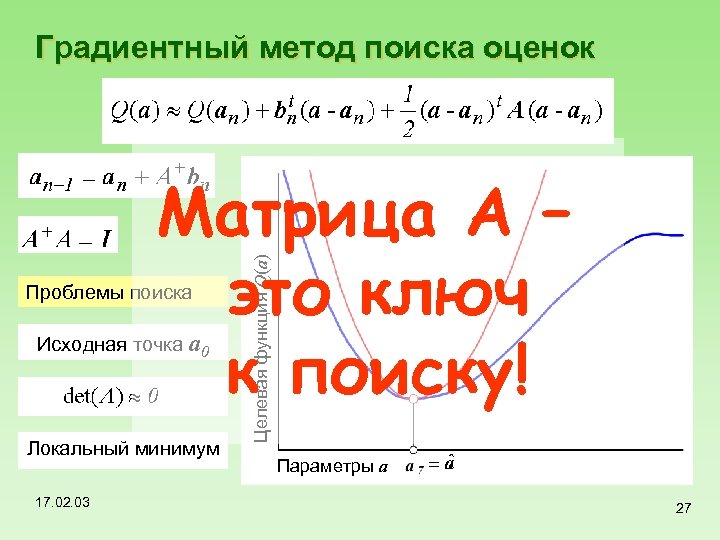Градиентный метод поиска оценок Проблемы поиска Исходная точка a 0 Локальный минимум 17. 02. 03 Целевая функция Q(a) Матрица A – это ключ к поиску! Параметры a 27

Точность оценивания (статистики) Матрица A – это мера качества оценивания! Матрица ковариаций Средне-квадратичные отклонения оценок Матрица корреляций F-матрица (Фишера) Оценка дисперсии и число степеней свободы 17. 02. 03 28

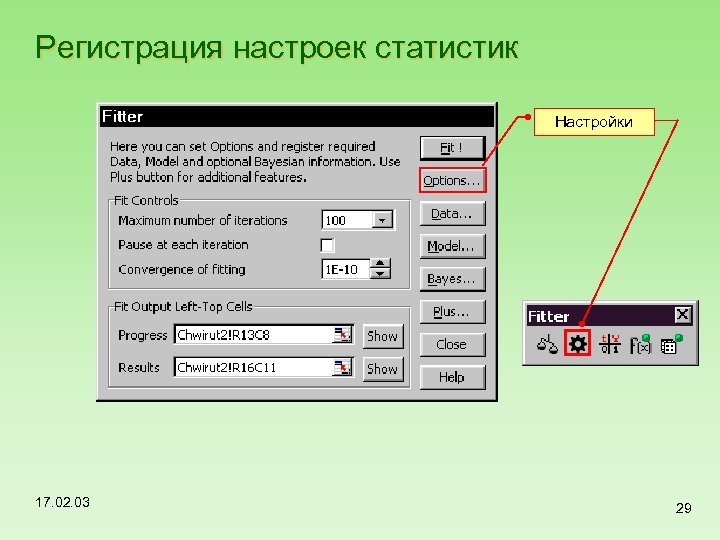Регистрация настроек статистик Настройки 17. 02. 03 29

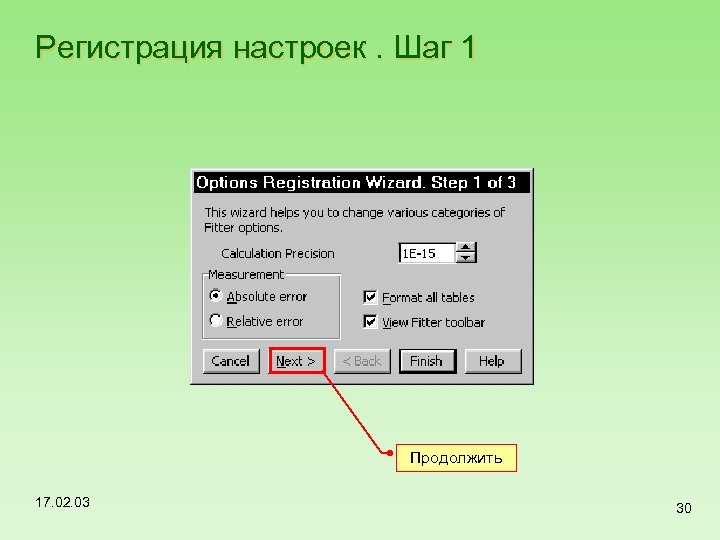Регистрация настроек. Шаг 1 Продолжить 17. 02. 03 30

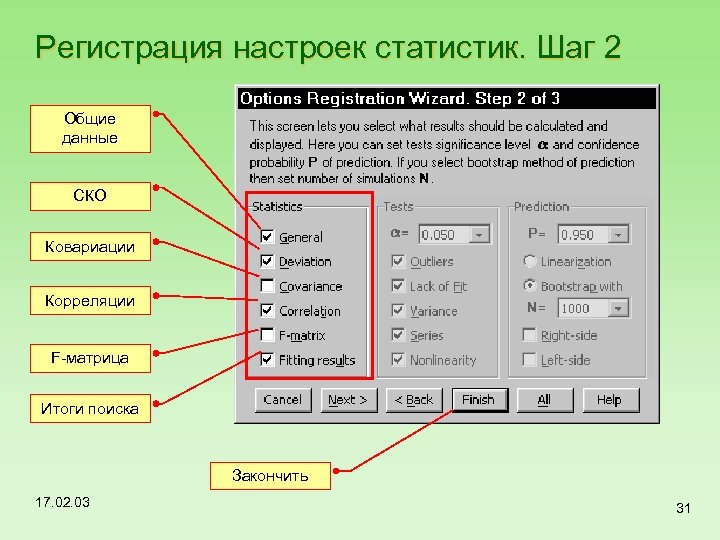Регистрация настроек статистик. Шаг 2 Общие данные СКО Ковариации Корреляции F-матрица Итоги поиска Закончить 17. 02. 03 31

5. Пример Box. Bod (NIST) Данные Модель Посмотрим, как работает Fitter Параметры Априорная (байесовская) информация 17. 02. 03 32

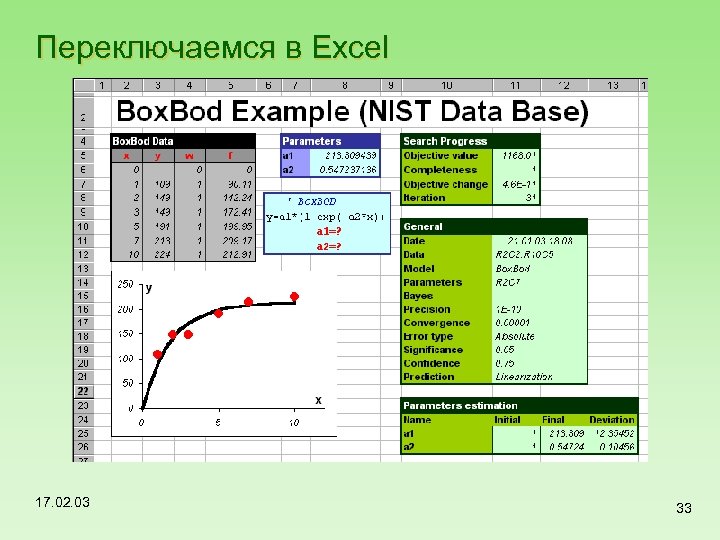Переключаемся в Excel 17. 02. 03 33

6. Прогноз 17. 02. 03 34

Достоверный прогноз должен учитывать погрешности в оценках Оценка отклика Доверительные границы Линеаризация 17. 02. 03 35

Имитационное прогнозирование Нелинейные модели требуют специальных методов достоверного прогноза 17. 02. 03 36

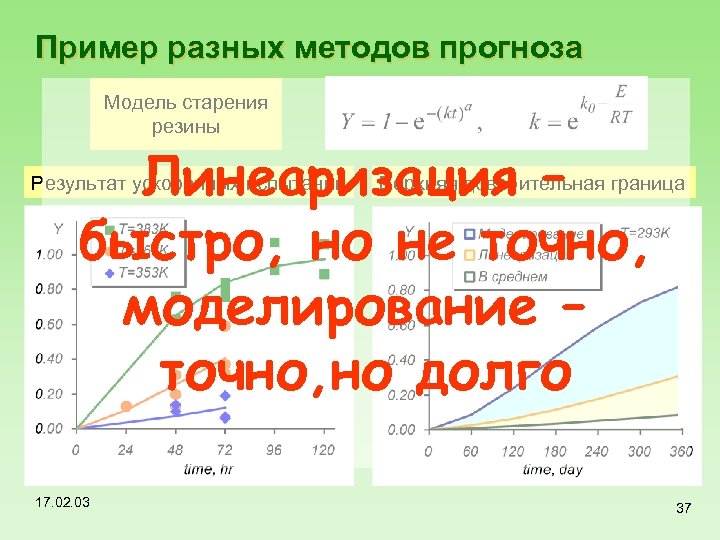Пример разных методов прогноза Модель старения резины Линеаризация – быстро, но не точно, моделирование – точно, но долго Результат ускоренных испытаний 17. 02. 03 Верхняя доверительная граница 37

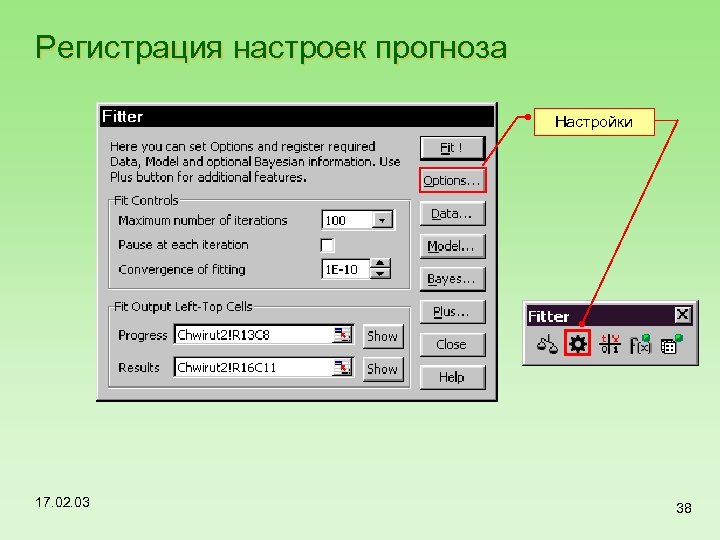Регистрация настроек прогноза Настройки 17. 02. 03 38

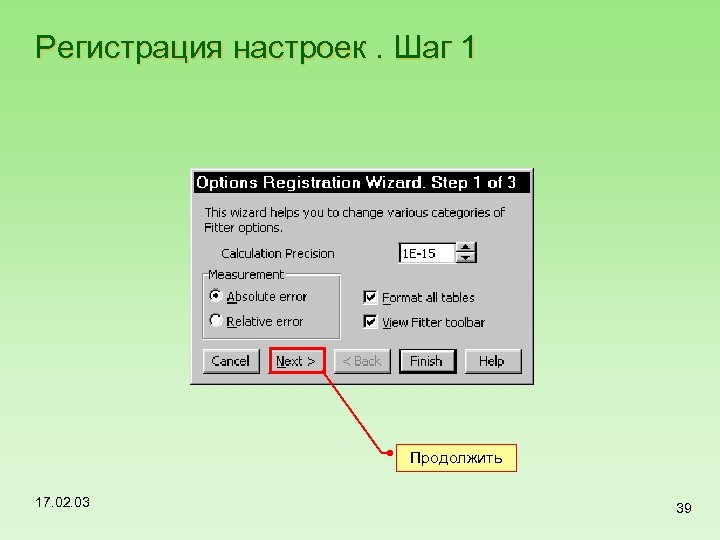Регистрация настроек. Шаг 1 Продолжить 17. 02. 03 39

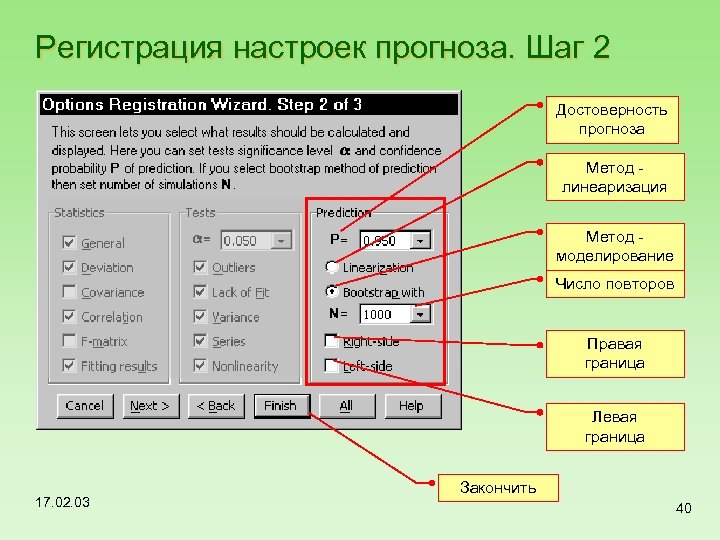Регистрация настроек прогноза. Шаг 2 Достоверность прогноза Метод линеаризация Метод моделирование Число повторов Правая граница Левая граница 17. 02. 03 Закончить 40

7. Тестирование модели 17. 02. 03 41

Проверка гипотез Статистика x сравнивается с критическим значением t (a) Из эксперимента 17. 02. 03 Тестовая статистика x Проверка не доказывает верности модели! Она только показывает, что гипотеза противоречит или не противоречит данным! Из теории 42

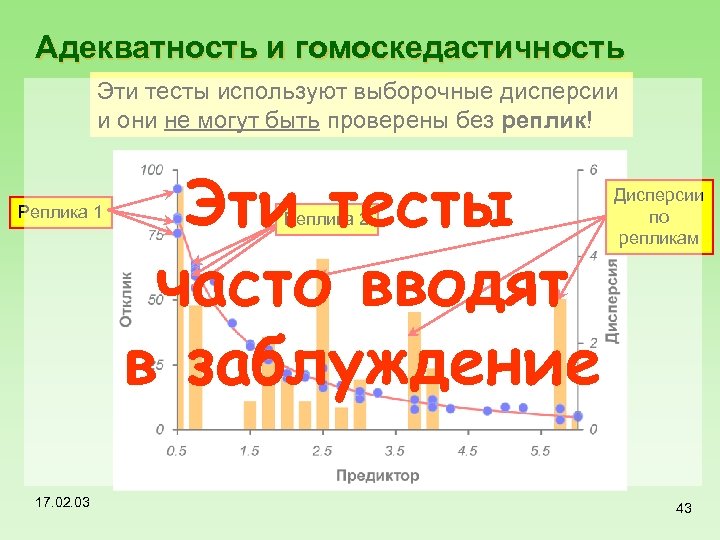Адекватность и гомоскедастичность Эти тесты используют выборочные дисперсии и они не могут быть проверены без реплик! Реплика 1 17. 02. 03 Эти тесты часто вводят в заблуждение Реплика 2 Дисперсии по репликам 43

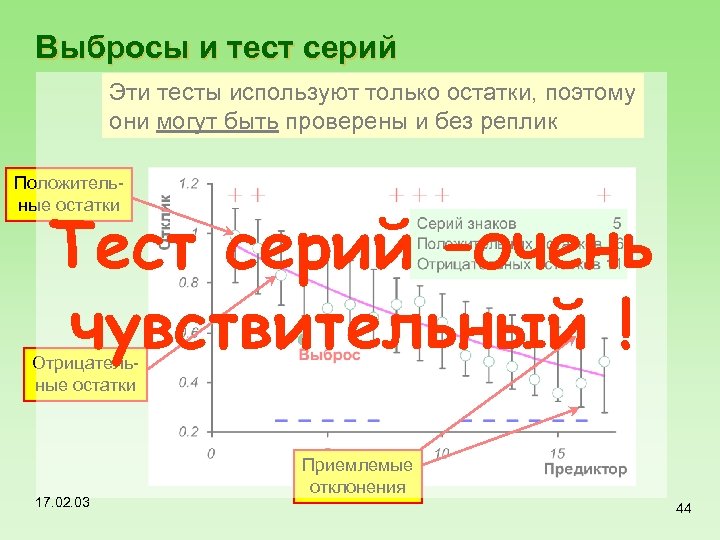Выбросы и тест серий Эти тесты используют только остатки, поэтому они могут быть проверены и без реплик Положительные остатки Тест серий –очень чувствительный ! Отрицательные остатки 17. 02. 03 Приемлемые отклонения 44

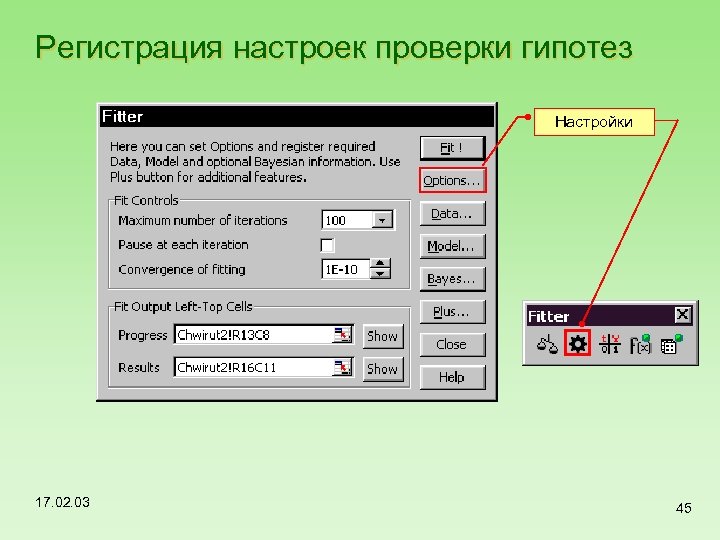Регистрация настроек проверки гипотез Настройки 17. 02. 03 45

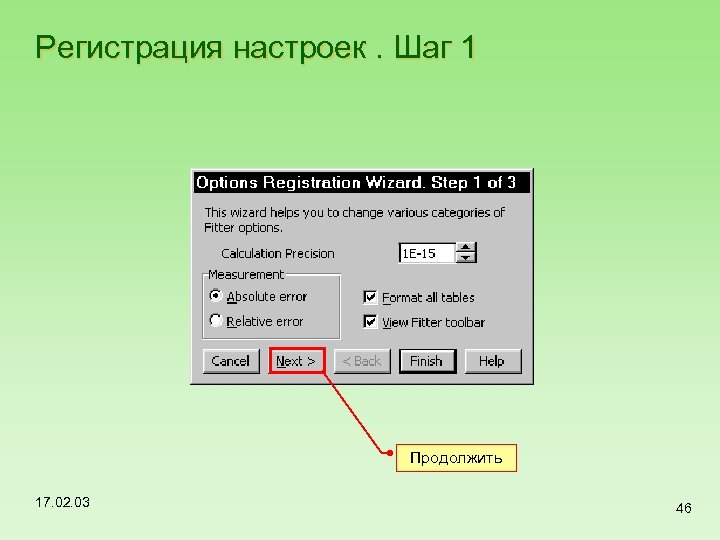Регистрация настроек. Шаг 1 Продолжить 17. 02. 03 46

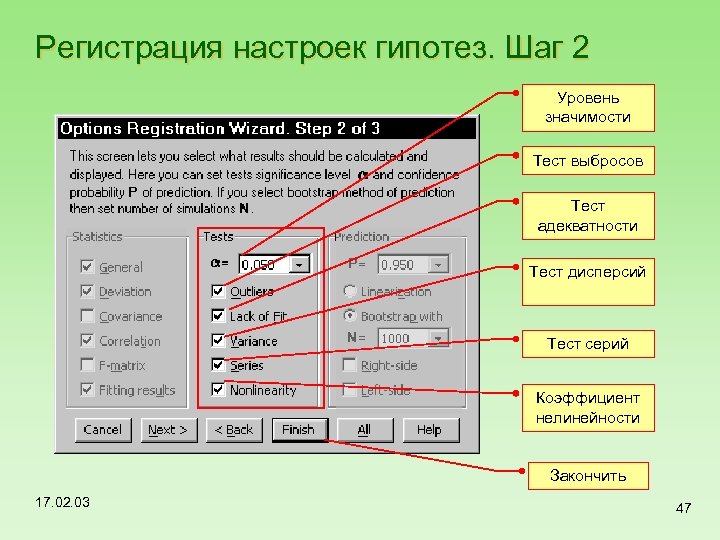Регистрация настроек гипотез. Шаг 2 Уровень значимости Тест выбросов Тест адекватности Тест дисперсий Тест серий Коэффициент нелинейности Закончить 17. 02. 03 47

8. Мультиколлинеарность 17. 02. 03 48

Что такое мультиколлинеарность Мультиколлинеарность – это вырождение матрицы A Целевая функция Q(a) Мультиколлинеарность – это наш главный враг! Разброс собственных значений: это мера вырождения матрицы A N(A) = 1 7 6 5 4 2 17. 02. 03 49

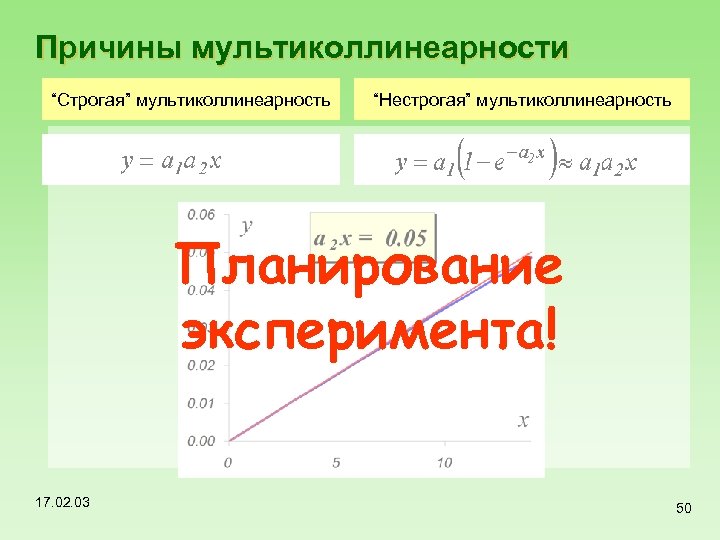Причины мультиколлинеарности “Строгая” мультиколлинеарность “Нестрогая” мультиколлинеарность Планирование эксперимента! 17. 02. 03 50

Подготовка данных и модели ((a + b) + c) + d a + (b + (c + d)) т. к. 1+10 – 20 = 1 64 -х битное представление числа в компьютере Компьютеру трудно – нужно ему помочь! 1 0 0 1 … 0 1 1 Средства Цель сделать матрицу A регулярной, т. е. уменьшить N(A) Шкалирование X m. X Центрирование X X – X 0 Перепараметризация 17. 02. 03 a (a) x (x) y (y) 51

Пример: закон Аррениуса Обычная форма записи Улучшенная форма записи Простые преобразования, дающие большой N(A) выигрыш! = 20 N(A) Шкалирование и центрирование Перепараметризация 17. 02. 03 52

Вычисление производных и точность N(A) A-1 y=f (a, x) 0=f (y, a, x) dy/dx=f (y, a, x) 6 10 8 6+2=8 10+2=12 8+2=10 8+0=8 12+0=12 10+0=10 8+2=10 10+2=12 12+2=14 14+2=16 10+2=12 12+2=14 1) Численное вычисление разностных производных 2) Автовычисление аналитических производных f=exp(-a*t) 17. 02. 03 df/da=-t*exp(-a*t) 53

9. Прогноз срока службы ПВХ изоляции 17. 02. 03 54

Постановка задачи Предсказать значения, которые нельзя измерить – это экстраполяция! Объект Кабельная изоляция из ПВХ Цель Прогноз срока службы Эксперимент Термогравиметрический метод Обработка Нелинейная регрессия + Fitter 17. 02. 03 55

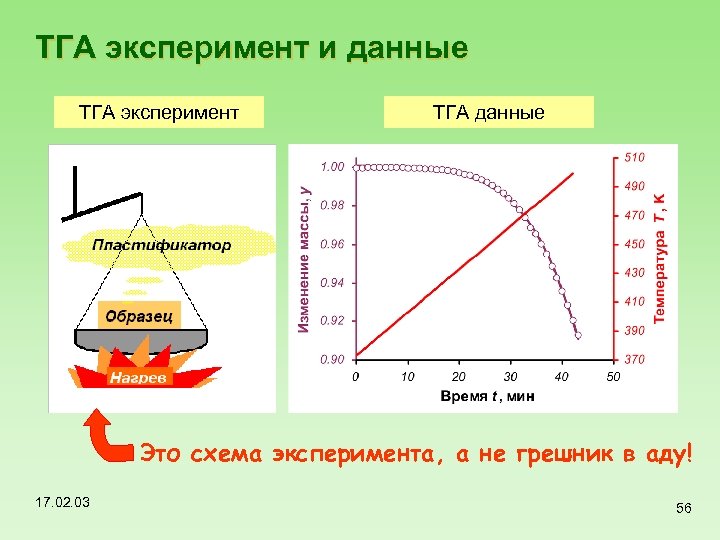ТГА эксперимент и данные ТГА эксперимент ТГА данные Это схема эксперимента, а не грешник в аду! 17. 02. 03 56

Переменные в примере ТГА Оцениваемые Измеряемые Нелинейная задача малой размерности! Отклик Промежуточные y=m/m 0 Изменение массы C Концентрация пластификатора Факторы Параметры t C 0 v T 0 F Время y 0 Начальное значение y Исходная концентрация k 0 Константа скорости испарения Скорость нагрева E Энергия активации Начальная температура Удельная поверхность образца 17. 02. 03 57

Модель испарения пластификатора Диффузия здесь не важна! Закон испарения Изменение объема Закон Аррениуса Рост температуры 17. 02. 03 58

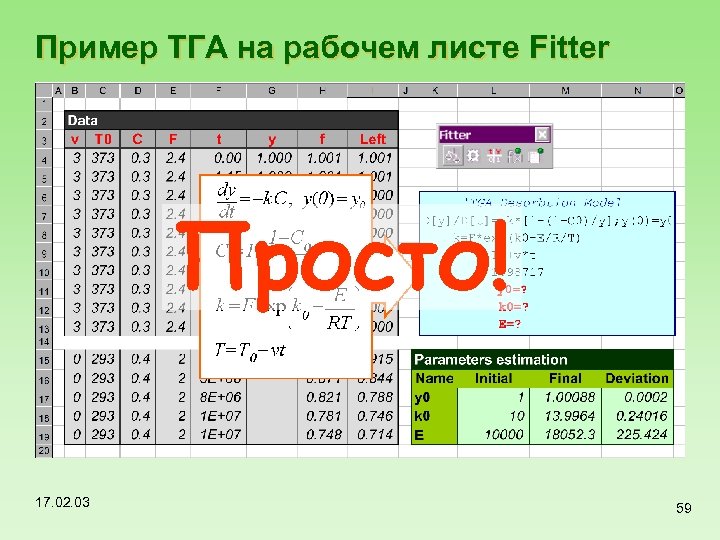Пример ТГА на рабочем листе Fitter Просто! 17. 02. 03 59

Прогноз срока службы На все условия, произвольный размер, с любой достоверностью! 17. 02. 03 60

10. Выводы Формальный подход Загадочная природа Содержательный подход Спасибо за внимание! 17. 02. 03 61