АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ Прямая на плоскости

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

Прямая на плоскости и ее уравнения Общее уравнение прямой. Уравнение первой степени относительно переменных х и у , т. е. уравнение вида при условии, что коэффициенты и одновременно не равны нулю, называется общим уравнением прямой. Отметим частные случаи общего уравнения прямой.

Уравнение прямой с угловым коэффициентом где угловой коэффициент – угол между прямой и осью Частные случаи:

Условия параллельности и перпендикулярности

Уравнение прямой, проходящей через данную точку Это уравнение можно рассматривать как уравнение пучка прямых, т. е. множества прямых, проходящих через одну и ту же точку плоскости.

Уравнение прямой, проходящей через две данные точки Угловой коэффициент прямой, проходящей через две точки , находится из соотношения

Уравнение прямой в отрезках на осях где и – соответственно абсцисса, и ордината точек пересечения прямой с осями ОХ и ОУ.

и , то координаты всякой третьей точки С, лежащей с ними на одной прямой, определяются формулами: и , где обозначает отношение, в котором точка С делит отрезок АВ, т. е. Каждой точке прямой АВ соответствует определенное значение параметра , и, обратно, каждомуединственная точка на прямой АВ. соответствует одна значению , и мы имеем: В частности, если точка С( x, y) делит отрезок АВ пополам, то и Деление отрезка в данном отношении. Если даны две точки.

Деление отрезка в данном отношении. Если даны две точки и , то координаты всякой третьей точки С, лежащей с ними на одной прямой, определяются формулами: где обозначает отношение, в котором точка С делит отрезок АВ, т. е. Каждой точке прямой АВ соответствует определенное значение параметра , и, обратно, каждому значению соответствует одна единственная точка на прямой АВ. В частности, если точка С( x, y) делит отрезок АВ пополам, то , и мы имеем: .

Полезные замечания. Три медианы треугольника пересекаются в одной точке (всегда внутри треугольника), являющейся центром тяжести треугольника. Эта точка делит каждую медиану в отношении 2: 1 (считая от вершины). Медиана делит треугольник на два равновеликих треугольника.

Пример 1. Через точку провести прямые параллельно, перпендикулярно и под углом к прямой (АВ): .

.

Кривые второго порядка Уравнение если А, В и С одновременно не равны нулю, задает на плоскости линии, которые называют кривыми II–го порядка. Если В=0 кривые имеют оси симметрии параллельные координатным осям. Будем рассматривать только этот случай.

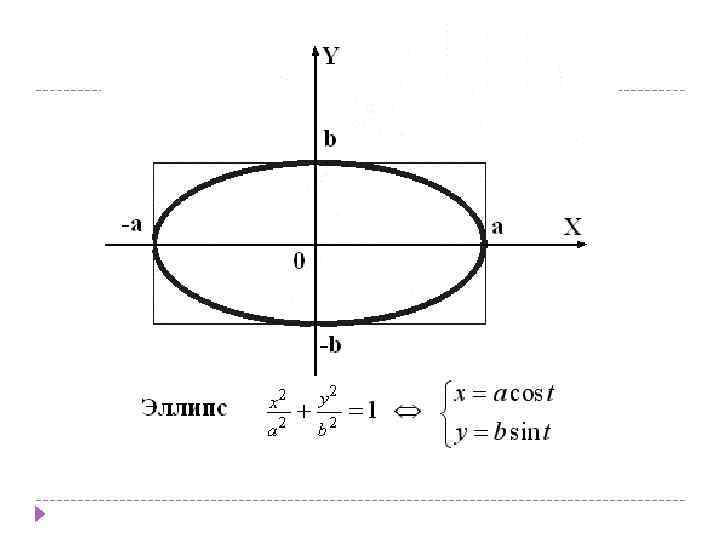
Выделяя полный квадрат, уравнение приводим к одному из следующих канонических видов: 1. – линии эллиптического типа: – эллипс с центром полуосями а и b. Если то уравнение запишется в виде – окружность с центром радиуса R.

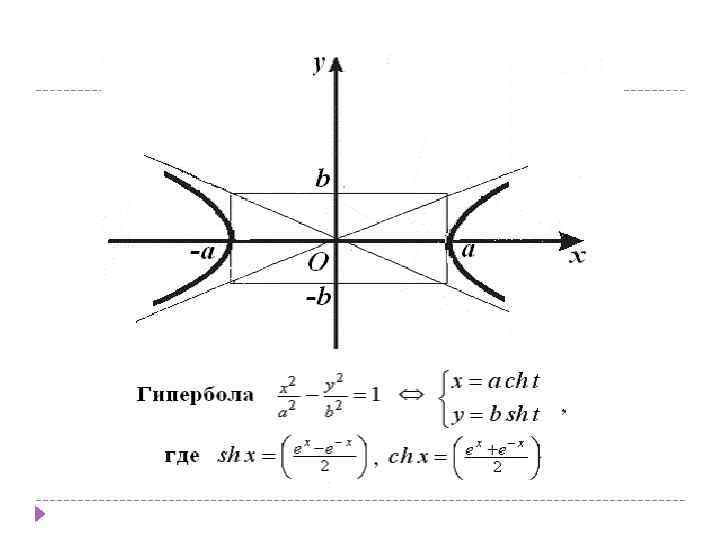
2. – линии гиперболического типа: – гипербола с центром вещественной полуосью – а, мнимой полуосью – b, или – сопряженная гипербола с центром вещественной полуосью – b, мнимой полуосью – а.

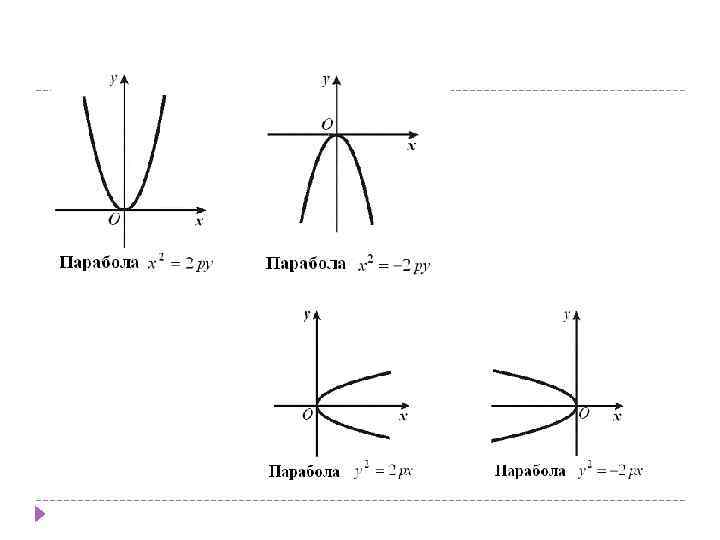
3. – линии параболического типа. Здесь возможны четыре случая: либо – параболы с вершиной В первом случае – ось симметрии параллельна оси ОХ, во втором – ОУ. Если в уравнении знак “+”, ветви параболы направлены в положительном направлении оси симметрии, знак “ –” — в противоположном.

Замечание. Возможны вырожденные случаи:

Пример: Установить вид кривой и построить ее график:

РЕШЕНИЕ: Выделим полные квадраты по переменным:

Это уравнение описывает гиперболу, центр симметрии которой находится в точке для построения введем новую систему координат В новой системе координат заданное уравнение принимает канонический вид

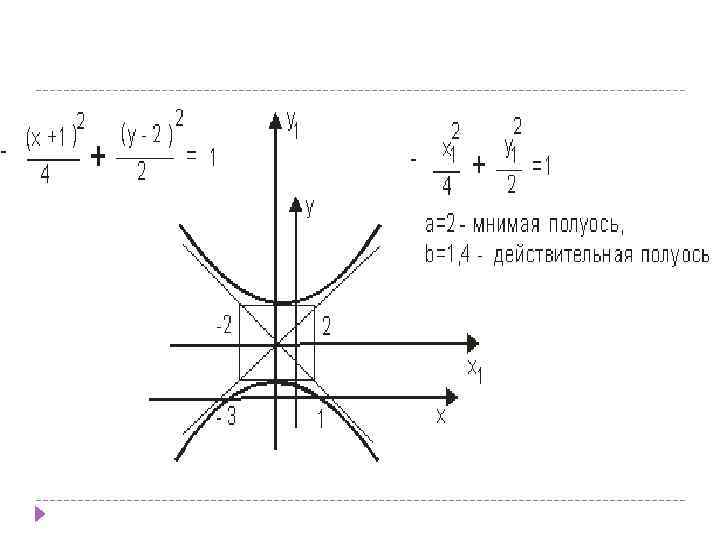
Определить тип кривой и построить