През Кривые второго порядка 1.ppt
- Количество слайдов: 26
 Аналитическая геометрия Лекции по математике для студентов I курса
Аналитическая геометрия Лекции по математике для студентов I курса
 Содержание n n Уравнение гиперболы Уравнение параболы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 2
Содержание n n Уравнение гиперболы Уравнение параболы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 2
 Уравнение гиперболы n Гипербола – это множество точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 3
Уравнение гиперболы n Гипербола – это множество точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 3
 Уравнение гиперболы n В соответствии с определением n Обозначим расстояние между фокусами 2 с, причём 2 a<2 c. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 4
Уравнение гиперболы n В соответствии с определением n Обозначим расстояние между фокусами 2 с, причём 2 a<2 c. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 4
 Уравнение гиперболы n Каноническое уравнение гиперболы, симметричной относительно осей координат, примет вид И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 5
Уравнение гиперболы n Каноническое уравнение гиперболы, симметричной относительно осей координат, примет вид И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 5
 Уравнение гиперболы n Обозначим вершины гиперболы буквами A 1 и A 2. n Координаты фокусов и вершин имеют вид: F 1(c, 0); F 2(c, 0); A 1(-a, 0); A 2 (a, 0). И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 1 A 2 6
Уравнение гиперболы n Обозначим вершины гиперболы буквами A 1 и A 2. n Координаты фокусов и вершин имеют вид: F 1(c, 0); F 2(c, 0); A 1(-a, 0); A 2 (a, 0). И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 1 A 2 6
 Уравнение гиперболы n n Параметр a называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы. Параметр b называют мнимой полуосью гиперболы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 1 A 2 7
Уравнение гиперболы n n Параметр a называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы. Параметр b называют мнимой полуосью гиперболы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 1 A 2 7
 Уравнение гиперболы n Отношение называется эксцентриситетом гиперболы. n Прямые, заданные уравнениями, называются асимптотами гиперболы. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 8
Уравнение гиперболы n Отношение называется эксцентриситетом гиперболы. n Прямые, заданные уравнениями, называются асимптотами гиперболы. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 8
 Уравнение гиперболы n Если параллельным сдвигом центр гиперболы разместить в точке с координатами уравнение гиперболы примет вид: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» , то 9
Уравнение гиперболы n Если параллельным сдвигом центр гиперболы разместить в точке с координатами уравнение гиперболы примет вид: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» , то 9
 Уравнение гиперболы n Каноническое уравнение гиперболы n Нормальное уравнение гиперболы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 10
Уравнение гиперболы n Каноническое уравнение гиперболы n Нормальное уравнение гиперболы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 10
 Пример Построить гиперболу если a=4, b=3. Решение. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 11
Пример Построить гиперболу если a=4, b=3. Решение. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 11
 Пример Найти координаты центра симметрии гиперболы, величину действительной и мнимой полуоси, координаты фокусов, уравнения асимптот, если гипербола задана уравнением Решение. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 12
Пример Найти координаты центра симметрии гиперболы, величину действительной и мнимой полуоси, координаты фокусов, уравнения асимптот, если гипербола задана уравнением Решение. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 12
 Решение Ответ. Координаты центра гиперболы (1; -3); величина действительной полуоси a=3, мнимой полуоси b=2; координаты фокусов: F 1(-5; 0) и F 2(-5; 0); уравнения асимптот: . И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 13
Решение Ответ. Координаты центра гиперболы (1; -3); величина действительной полуоси a=3, мнимой полуоси b=2; координаты фокусов: F 1(-5; 0) и F 2(-5; 0); уравнения асимптот: . И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 13
 Уравнение гиперболы, асимптотами которой являются оси координат В школьном курсе математики изучаются функции , k>0 графиками которых являются гиперболы. Асимптотами этих гипербол являются оси Ox и Oy. Если k>0, то ветви гиперболы лежат в первой и третьей четверти декартовой системы координат, при k<0 во второй и четвёртой. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 14
Уравнение гиперболы, асимптотами которой являются оси координат В школьном курсе математики изучаются функции , k>0 графиками которых являются гиперболы. Асимптотами этих гипербол являются оси Ox и Oy. Если k>0, то ветви гиперболы лежат в первой и третьей четверти декартовой системы координат, при k<0 во второй и четвёртой. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 14
 Уравнение гиперболы, асимптотами которой являются оси координат n n Иначе уравнение гиперболы можно записать: Можно показать, что координаты фокусов и вершин гиперболы при k >0 имеют вид: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 15
Уравнение гиперболы, асимптотами которой являются оси координат n n Иначе уравнение гиперболы можно записать: Можно показать, что координаты фокусов и вершин гиперболы при k >0 имеют вид: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 15
 Уравнение гиперболы, асимптотами которой являются оси координат n Если параллельным сдвигом центр гиперболы разместить в точке с координатами (xо, yо), то уравнение гиперболы примет вид: n Соответственно, получат сдвиг и координаты фокусов и вершин. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 16
Уравнение гиперболы, асимптотами которой являются оси координат n Если параллельным сдвигом центр гиперболы разместить в точке с координатами (xо, yо), то уравнение гиперболы примет вид: n Соответственно, получат сдвиг и координаты фокусов и вершин. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 16
 График дробно-линейной функции n Рассмотрим функцию Такие функции называются дробнолинейными. Покажем, что графиком этой функции также является гипербола. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 17
График дробно-линейной функции n Рассмотрим функцию Такие функции называются дробнолинейными. Покажем, что графиком этой функции также является гипербола. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 17
 Пример. Доказать, что графиком функции является гипербола. Найти координаты фокусов и вершин. Построить график. Решение. Выполним преобразования: Мы получили уравнение гиперболы, центр симметрии которой имеет координаты (-1; 2), параметр k=1. Фокусы и вершины задаются координатами: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 18
Пример. Доказать, что графиком функции является гипербола. Найти координаты фокусов и вершин. Построить график. Решение. Выполним преобразования: Мы получили уравнение гиперболы, центр симметрии которой имеет координаты (-1; 2), параметр k=1. Фокусы и вершины задаются координатами: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 18
 Уравнение параболы n Парабола – это множество точек, одинаково удалённых от данной точки (фокуса) и от данной прямой (директрисы). И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 19
Уравнение параболы n Парабола – это множество точек, одинаково удалённых от данной точки (фокуса) и от данной прямой (директрисы). И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 19
 Уравнение параболы n Обозначим расстояние от вершины параболы до фокуса буквой p/2, фокус F. n Из определения следует, что MK=MF И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 20
Уравнение параболы n Обозначим расстояние от вершины параболы до фокуса буквой p/2, фокус F. n Из определения следует, что MK=MF И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 20
 Уравнение параболы n n Каноническое уравнение параболы, вершина которой совпадает с началом координат, а ось симметрии с осью , имеет вид: Уравнение директрисы: Фокус имеет координаты: Вершина данной параболы находится в начале координат. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 21
Уравнение параболы n n Каноническое уравнение параболы, вершина которой совпадает с началом координат, а ось симметрии с осью , имеет вид: Уравнение директрисы: Фокус имеет координаты: Вершина данной параболы находится в начале координат. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 21
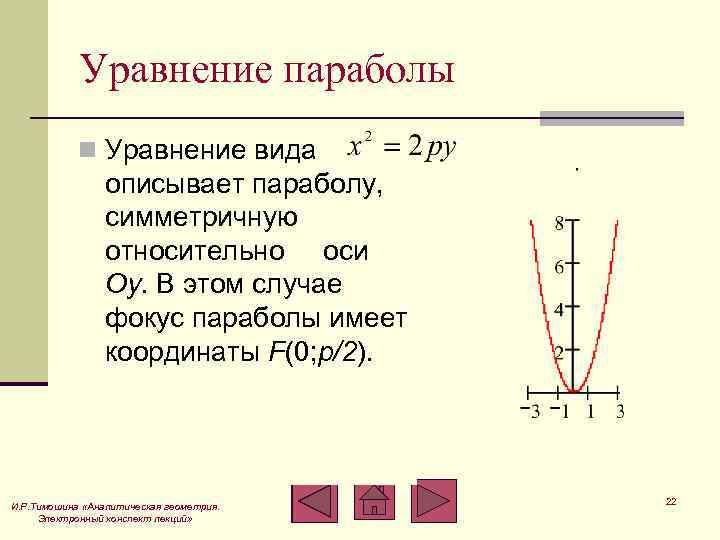 Уравнение параболы n Уравнение вида описывает параболу, симметричную относительно оси Oy. В этом случае фокус параболы имеет координаты F(0; p/2). И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 22
Уравнение параболы n Уравнение вида описывает параболу, симметричную относительно оси Oy. В этом случае фокус параболы имеет координаты F(0; p/2). И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 22
 Уравнение параболы n Если параллельным сдвигом центр параболы разместить в точке с координатами , то уравнение параболы будет иметь вид: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 23
Уравнение параболы n Если параллельным сдвигом центр параболы разместить в точке с координатами , то уравнение параболы будет иметь вид: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 23
 Пример Уравнение параболы имеет вид: Найти координаты вершины этой параболы, координаты фокуса и уравнение директрисы. Решение. Преобразуем правую часть уравнения: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 24
Пример Уравнение параболы имеет вид: Найти координаты вершины этой параболы, координаты фокуса и уравнение директрисы. Решение. Преобразуем правую часть уравнения: И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 24
 Решение Преобразуем правую часть уравнения: Сравнив полученное уравнение с уравнением убеждаемся, что координаты вершины параболы (-2; -11); параметр p=0, 25. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 25
Решение Преобразуем правую часть уравнения: Сравнив полученное уравнение с уравнением убеждаемся, что координаты вершины параболы (-2; -11); параметр p=0, 25. И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» 25
 Ответ Координаты вершины параболы координаты фокуса уравнение директрисы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» (-2; -11); ; 26
Ответ Координаты вершины параболы координаты фокуса уравнение директрисы И. Р. Тимошина «Аналитическая геометрия. Электронный конспект лекций» (-2; -11); ; 26


