 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ l. ПЛОСКАЯ ЛИНИЯ И ЕЕ УРАВНЕНИЕ В R 2 l. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ l. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ l. УРАВНЕНИЕ ПРЯМОЙ ПО ДВУМ ТОЧКАМ l. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ КОЭФФИЦИЕНТУ УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ КОЭФФИЦИЕНТОМ. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ l. ПЛОСКАЯ ЛИНИЯ И ЕЕ УРАВНЕНИЕ В R 2 l. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ l. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ l. УРАВНЕНИЕ ПРЯМОЙ ПО ДВУМ ТОЧКАМ l. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ КОЭФФИЦИЕНТУ УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ КОЭФФИЦИЕНТОМ. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
 ПРИМЕР l Построить линию, заданную уравнением l Придавая переменной различные числовые значения и вычисляя соответствующие значения , построим таблицу Введем на плоскости декартову систему координат и построим на этой плоскости соответствующие точки с координатами. Соединяя построенные точки линией, получим искомую кривую l
ПРИМЕР l Построить линию, заданную уравнением l Придавая переменной различные числовые значения и вычисляя соответствующие значения , построим таблицу Введем на плоскости декартову систему координат и построим на этой плоскости соответствующие точки с координатами. Соединяя построенные точки линией, получим искомую кривую l
 ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ l. Положение прямой на координатной плоскости вполне определяется заданием lлюбых двух ее точек lточки и вектора, параллельного прямой lточки и вектора, перпендикулярного прямой lуглового коэффициента и отрезка, отсекаемого прямой от оси OY lдругих величин.
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ l. Положение прямой на координатной плоскости вполне определяется заданием lлюбых двух ее точек lточки и вектора, параллельного прямой lточки и вектора, перпендикулярного прямой lуглового коэффициента и отрезка, отсекаемого прямой от оси OY lдругих величин.
 Уравнение прямой по точке и нормальному вектору l
Уравнение прямой по точке и нормальному вектору l
 Рассмотрим два случая: l
Рассмотрим два случая: l
 УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ l
УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ l
 Рассмотрим два случая: l
Рассмотрим два случая: l
 Замечание
Замечание
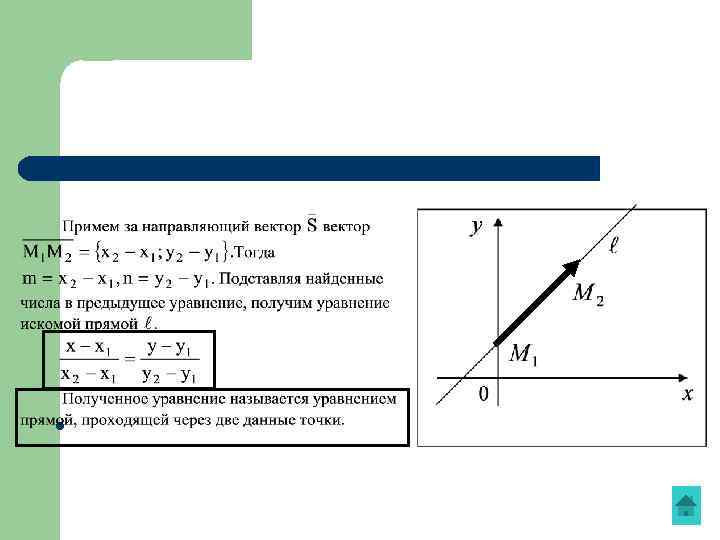 l
l
 УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ КОЭФФИЦИЕНТУ l
УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ КОЭФФИЦИЕНТУ l