Аналитическая геометрия Декартовы и полярные координаты точки

Аналитическая геометрия

Декартовы и полярные координаты точки Декартова система координат Декартовой прямоугольной системой координат в пространстве (на плоскости) называется совокупность некоторой точки О, называемой началом координат, и ортонормированного базиса Оси, проведенные через начало координат в направлении векторов , называются соответственно осями Ох, Оу, Оz (Ох, Оу). Радиус-вектор точки М есть вектор

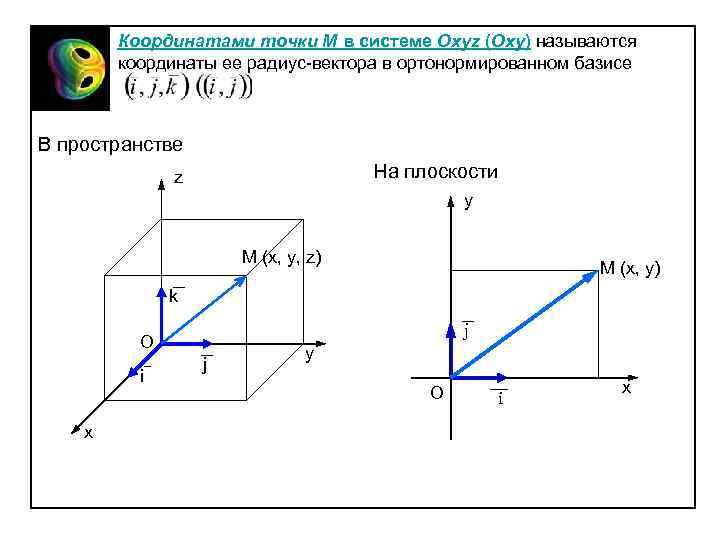Координатами точки М в системе Oxyz (Oxy) называются координаты ее радиус-вектора в ортонормированном базисе В пространстве На плоскости z y M (x, y, z) M (x, y) k j O i x j y O i x

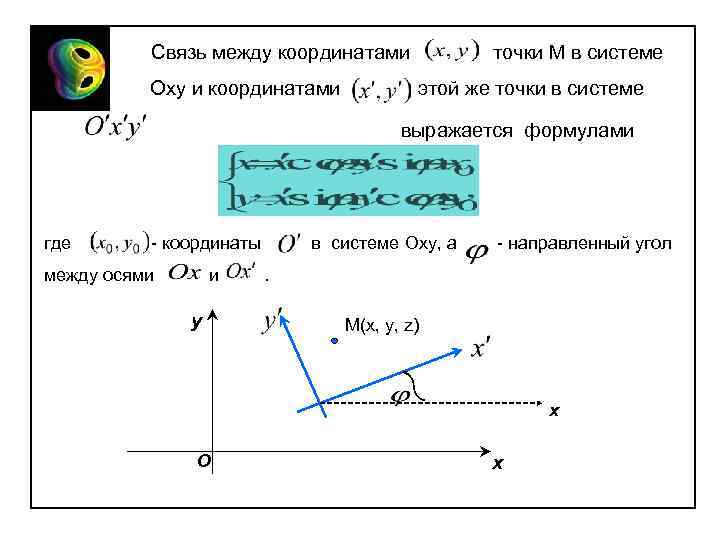Связь между координатами Oxy и координатами точки М в системе этой же точки в системе выражается формулами где - координаты между осями и y в системе Oxy, а - направленный угол . М(x, y, z) x О x

Полярная система координат Полярной системой координат на плоскости называется совокупность точки О, называемой полюсом, и выходящего из нее луча Ох, называемого полярной осью. Полярными координатами точки М на плоскости являются - полярный радиус и - полярный угол, причем М r О х

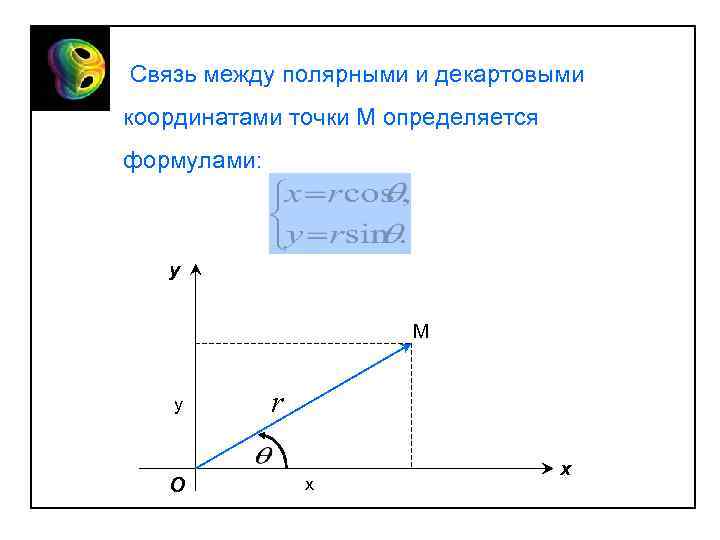Связь между полярными и декартовыми координатами точки М определяется формулами: y M y O r x x

Простейшие задачи аналитической геометрии Расстояние между точками формулой и выражается

Координаты точки М, делящей направленный отрезок в отношении , определяются формулами: Координаты середины отрезка выражаются формулами:

Уравнения линии и поверхности у L х Уравнение есть уравнение линии L на плоскости в заданной декартовой системе координат, если этому уравнению удовлетворяют координаты любой точки принадлежащей линии L , и не удовлетворяют координаты любой точки не принадлежащей L.

Пример. Вывести уравнение окружности радиуса r c центром в точке . у b С a х

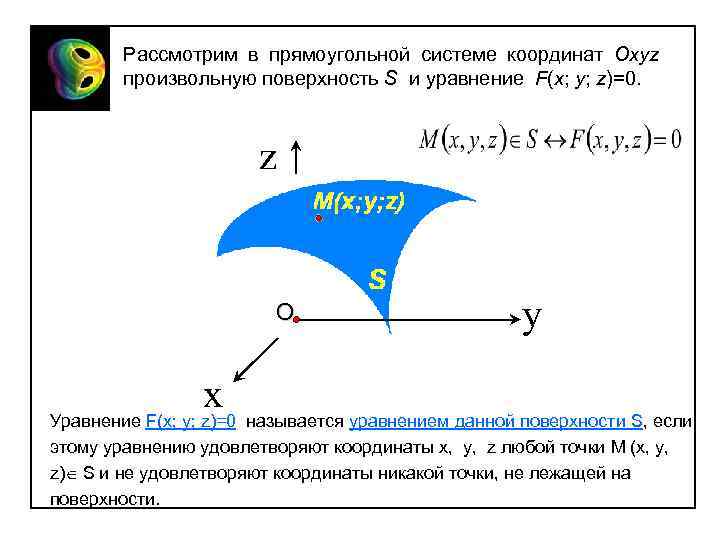Рассмотрим в прямоугольной системе координат Oxyz произвольную поверхность S и уравнение F(x; y; z)=0. z О x y Уравнение F(x; y; z)=0 называется уравнением данной поверхности S, если этому уравнению удовлетворяют координаты x, y, z любой точки M (x, y, z) S и не удовлетворяют координаты никакой точки, не лежащей на поверхности.

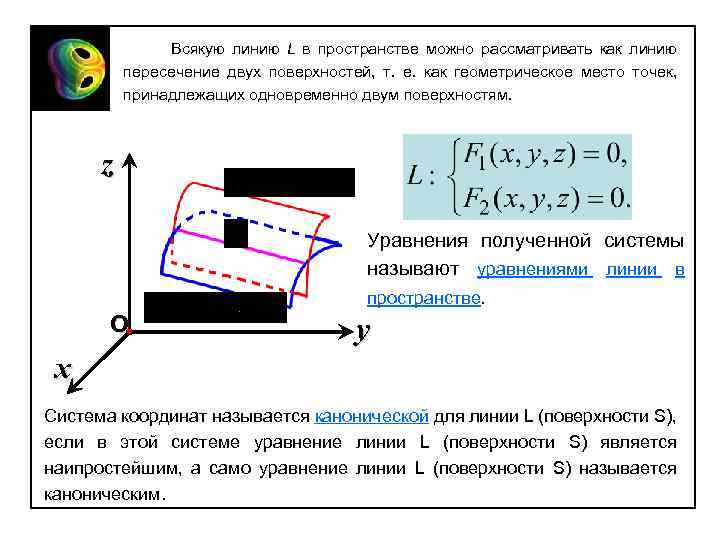Всякую линию L в пространстве можно рассматривать как линию пересечение двух поверхностей, т. е. как геометрическое место точек, принадлежащих одновременно двум поверхностям. z Уравнения полученной системы называют уравнениями линии в пространстве. О y x Система координат называется канонической для линии L (поверхности S), если в этой системе уравнение линии L (поверхности S) является наипростейшим, а само уравнение линии L (поверхности S) называется каноническим.

ПРЯМАЯ НА ПЛОСКОСТИ Линия L на плоскости называется линией первого порядка, если в некоторой декартовой системе координат Oxy эта линия определяется уравнением первой степени относительно переменных x, y. Теорема. В декартовой прямоугольной системе координат любая прямая определяется уравнением первой степени , и наоборот, любое уравнение первой степени определяет прямую на плоскости. Общее уравнение прямой L на плоскости y L x

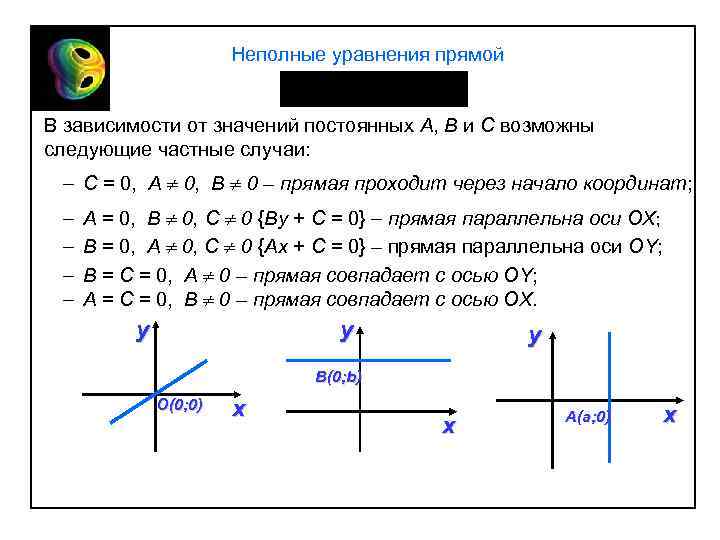Неполные уравнения прямой В зависимости от значений постоянных A, B и C возможны следующие частные случаи: C = 0, А 0, В 0 – прямая проходит через начало координат; А = 0, В 0, С 0 {By + C = 0} прямая параллельна оси OX; В = 0, А 0, С 0 {Ax + C = 0} – прямая параллельна оси ОY; В = С = 0, А 0 – прямая совпадает с осью ОY; А = С = 0, В 0 – прямая совпадает с осью OX. у у у B(0; b) O(0; 0) х х A(a; 0) х

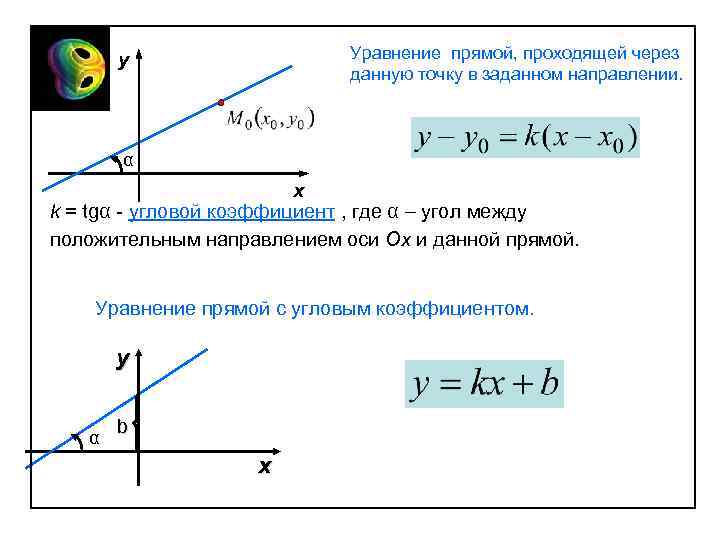Уравнение прямой, проходящей через данную точку в заданном направлении. y α x k = tgα - угловой коэффициент , где α угол между положительным направлением оси Oх и данной прямой. Уравнение прямой с угловым коэффициентом. у α b х

Направляющий вектор прямой – любой ненулевой вектор, параллельный этой прямой. Каноническое уравнение прямой у L х Параметрические уравнения прямой

Уравнение прямой, проходящей через две точки y x у Уравнение прямой в отрезках B(0; b) b A(a; 0) a х В уравнении в отрезках числа a и b имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает прямая на осях Oх и Oy соответственно (отрезки отсчитываются от начала координат).

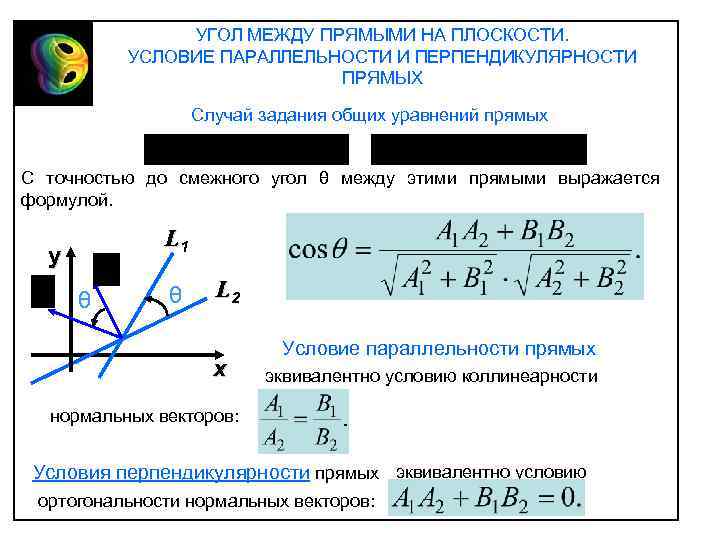УГОЛ МЕЖДУ ПРЯМЫМИ НА ПЛОСКОСТИ. УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ Случай задания общих уравнений прямых С точностью до смежного угол θ между этими прямыми выражается формулой. L 1 y θ θ L 2 х Условие параллельности прямых эквивалентно условию коллинеарности нормальных векторов: Условия перпендикулярности прямых эквивалентно условию ортогональности нормальных векторов:

Случай задания прямых уравнением с угловым коэффициентом Найдем угол θ между этими прямыми. y l 2 θ φ1 l 1 Условие параллельности прямых φ2 х Условие перпендикулярности прямых

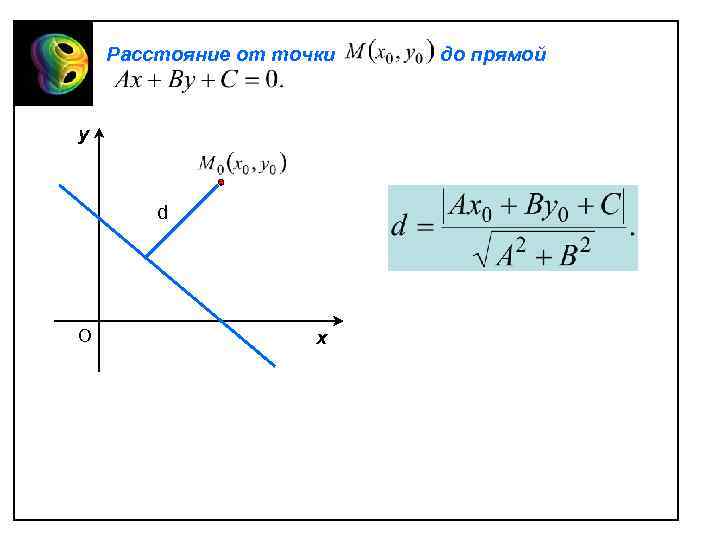Расстояние от точки y d О х до прямой

Плоскость в пространстве Поверхность S называется поверхностью первого порядка, если в декартовой системе Oxyz эта поверхность определяется уравнением первой степени с тремя переменными x, y, z. Теорема. В декартовой прямоугольной системе координат любая плоскость определяется уравнением первой степени c тремя переменными и, обратно, всякое уравнение Ax + By + Cz+ D = 0 первой степени определяет плоскость в пространстве. Общее уравнение плоскости z S y x

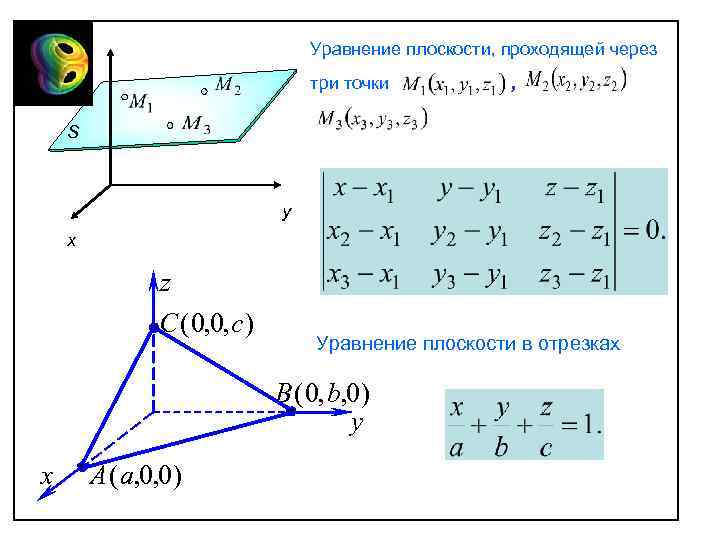Уравнение плоскости, проходящей через z три точки , S y x z C ( 0, 0, c ) Уравнение плоскости в отрезках B ( 0, b, 0 ) y x A (a, 0, 0 )

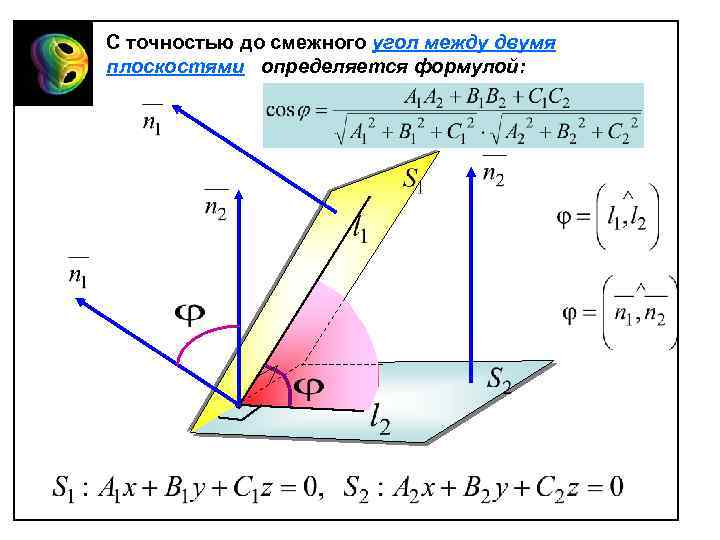С точностью до смежного угол между двумя плоскостями определяется формулой:

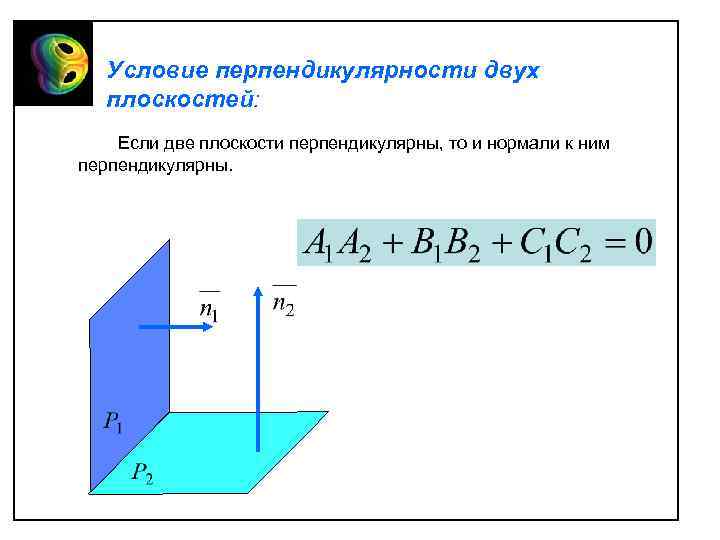Условие перпендикулярности двух плоскостей: Если две плоскости перпендикулярны, то и нормали к ним перпендикулярны.

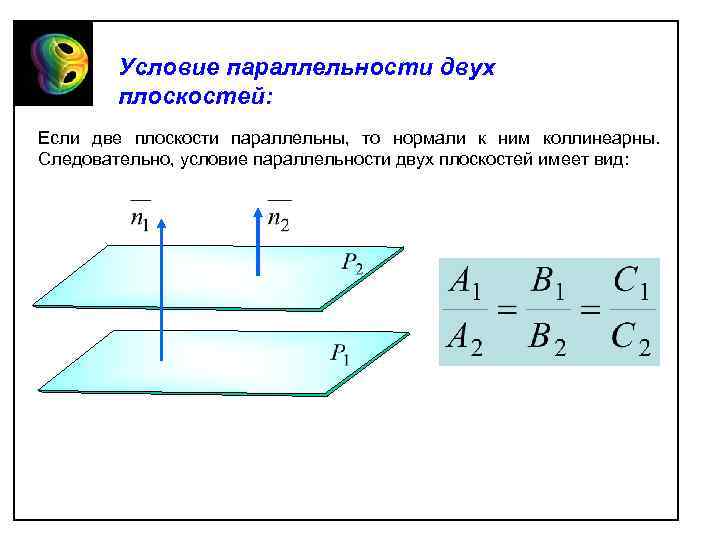Условие параллельности двух плоскостей: Если две плоскости параллельны, то нормали к ним коллинеарны. Следовательно, условие параллельности двух плоскостей имеет вид:

Расстоянием от точки до плоскости (не проходящей через эту точку) называется длина перпендикуляра, опущенного из точки на эту плоскость. Пусть плоскость Р задана уравнением Ax+By+Cz+D=0 и дана точка M 0(x 0; y 0; z 0). Тогда расстояние d от точки M 0 до плоскости Р определяется по формуле M 0(x 0; y 0; z 0) d Р

ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ Прямую L в пространстве можно рассматривать как линию пересечения двух плоскостей P 1 и P 2. L Данная система называется общими уравнениями прямой L в пространстве. Уравнения прямой в пространстве, проходящей через две точки z y х

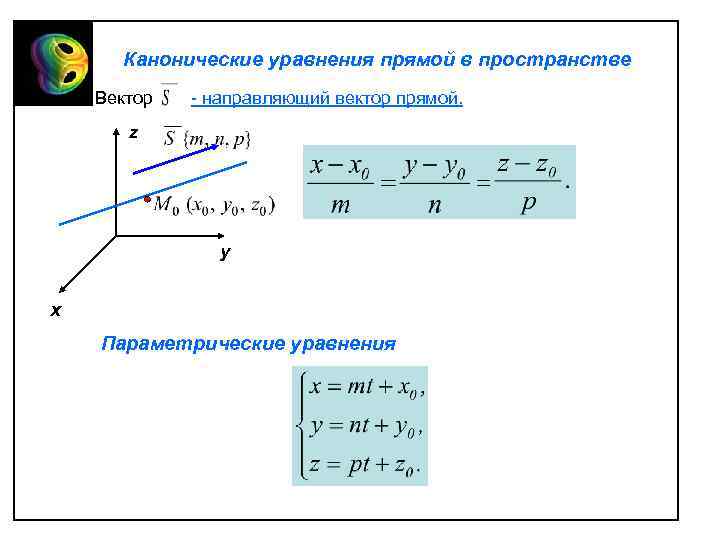Канонические уравнения прямой в пространстве Вектор - направляющий вектор прямой. z y x Параметрические уравнения

С точностью до смежного угол между двумя прямыми в пространстве определяется формулой: Прямые параллельны Прямые перпендикулярны

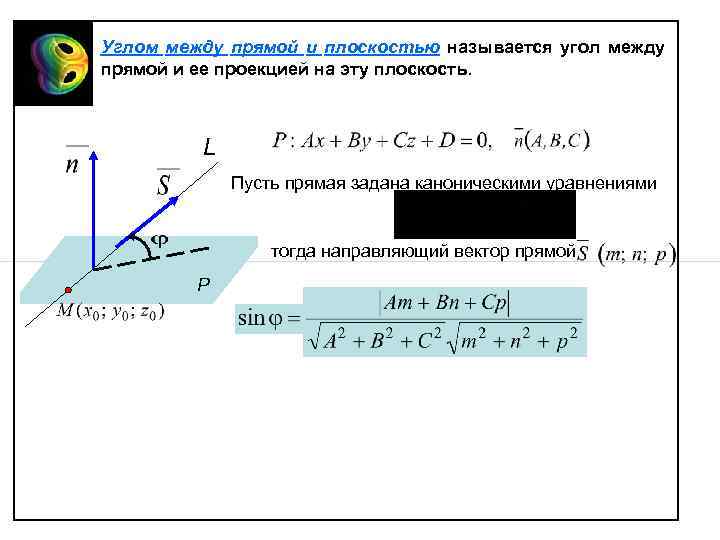Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. L Пусть прямая задана каноническими уравнениями тогда направляющий вектор прямой Р