An Overview of High Performance Computing and Challenges

An Overview of High Performance Computing and Challenges for the Future Jack Dongarra INNOVATIVE COMP ING LABORATORY University of Tennessee Oak Ridge National Laboratory University of Manchester 3/15/2018 1

Outline • Top 500 Results • Four Important Concepts that Will Effect Math Software § Effective Use of Many-Core § Exploiting Mixed Precision in Our Numerical Computations § Self Adapting / Auto Tuning of Software § Fault Tolerant Algorithms 2

H. Meuer, H. Simon, E. Strohmaier, & JD Rate - Listing of the 500 most powerful Computers in the World - Yardstick: Rmax from LINPACK MPP Ax=b, dense problem TPP performance - Updated twice a year Size SC‘xy in the States in November Meeting in Germany in June - All data available from www. top 500. org 3

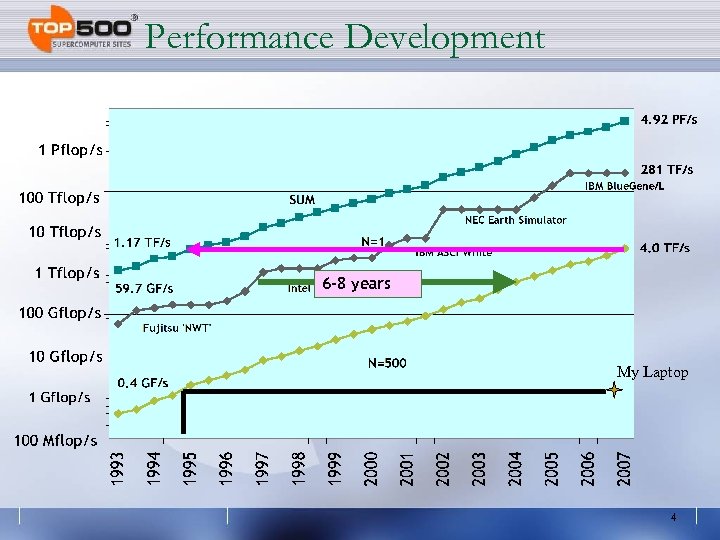Performance Development 6 -8 years My Laptop 4

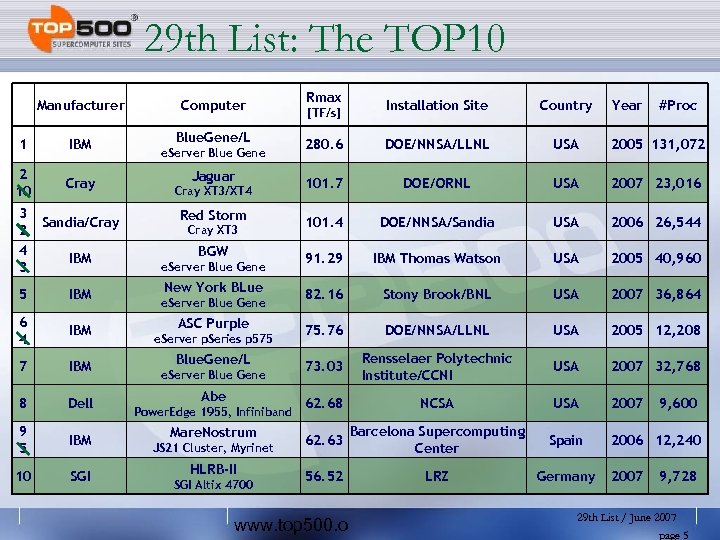29 th List: The TOP 10 Manufacturer 1 IBM 2 10 Cray 3 2 4 3 Sandia/Cray IBM 5 IBM 6 4 IBM 7 IBM 8 Dell 9 5 IBM 10 SGI Computer Blue. Gene/L e. Server Blue Gene Jaguar Cray XT 3/XT 4 Red Storm Cray XT 3 BGW e. Server Blue Gene New York BLue e. Server Blue Gene ASC Purple e. Server p. Series p 575 Blue. Gene/L e. Server Blue Gene Abe Power. Edge 1955, Infiniband Mare. Nostrum JS 21 Cluster, Myrinet HLRB-II SGI Altix 4700 Rmax Installation Site Country 280. 6 DOE/NNSA/LLNL USA 2005 131, 072 101. 7 DOE/ORNL USA 2007 23, 016 101. 4 DOE/NNSA/Sandia USA 2006 26, 544 91. 29 IBM Thomas Watson USA 2005 40, 960 82. 16 Stony Brook/BNL USA 2007 36, 864 75. 76 DOE/NNSA/LLNL USA 2005 12, 208 73. 03 Rensselaer Polytechnic Institute/CCNI USA 2007 32, 768 62. 68 NCSA USA 2007 62. 63 Barcelona Supercomputing Center Spain 56. 52 LRZ Germany [TF/s] www. top 500. o Year #Proc 9, 600 2006 12, 240 2007 9, 728 29 th List / June 2007 page 5

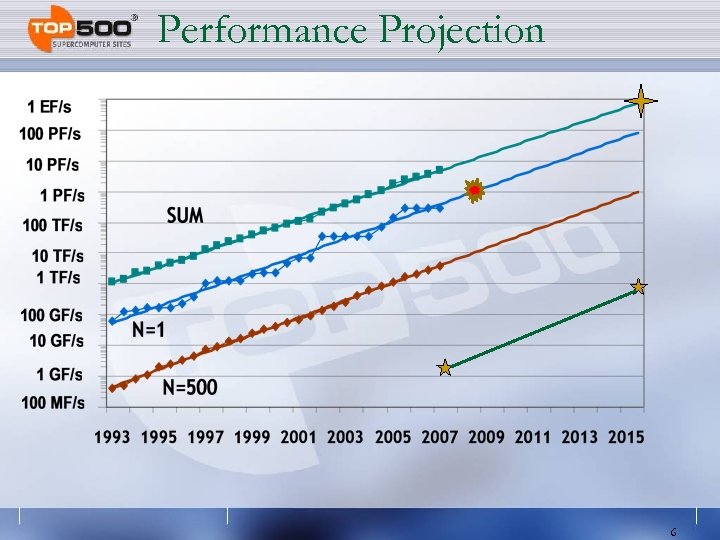Performance Projection 6

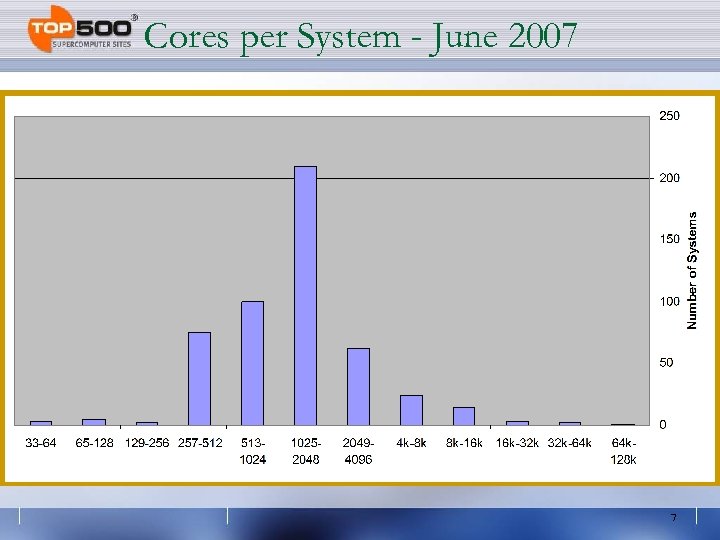Cores per System - June 2007 7

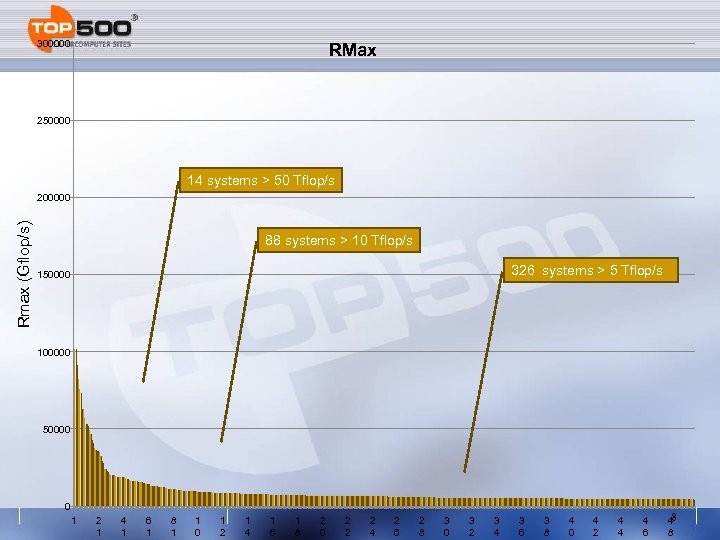300000 RMax 250000 14 systems > 50 Tflop/s Rmax (Gflop/s) 200000 88 systems > 10 Tflop/s 326 systems > 5 Tflop/s 150000 100000 50000 0 1 2 1 4 1 6 1 8 1 1 0 1 2 1 4 1 6 1 8 2 0 2 2 2 4 2 6 2 8 3 0 3 2 3 4 3 6 3 8 4 0 4 2 4 4 4 6 8 4 8

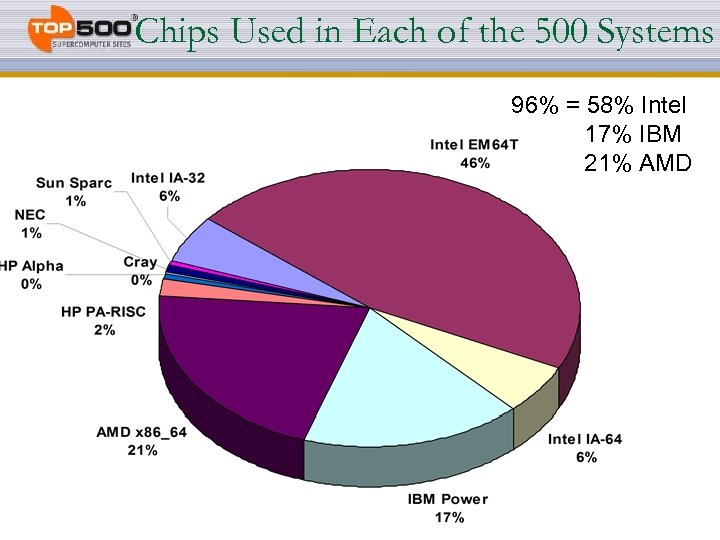Chips Used in Each of the 500 Systems 96% = 58% Intel 17% IBM 21% AMD 9

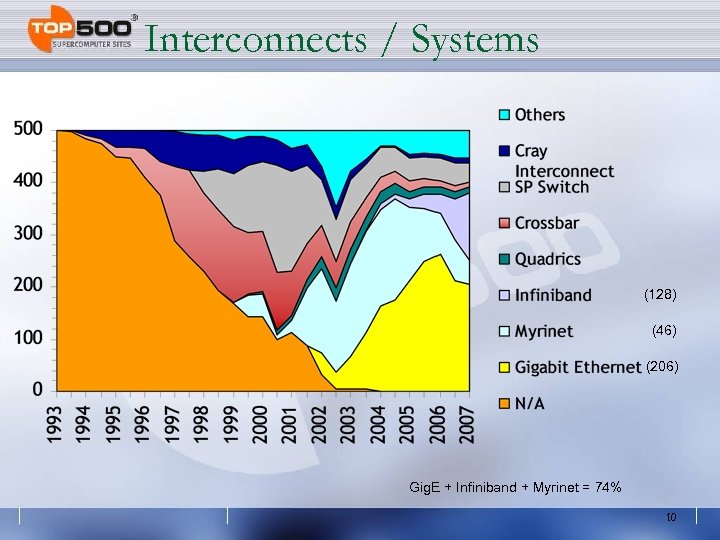Interconnects / Systems (128) (46) (206) Gig. E + Infiniband + Myrinet = 74% 10

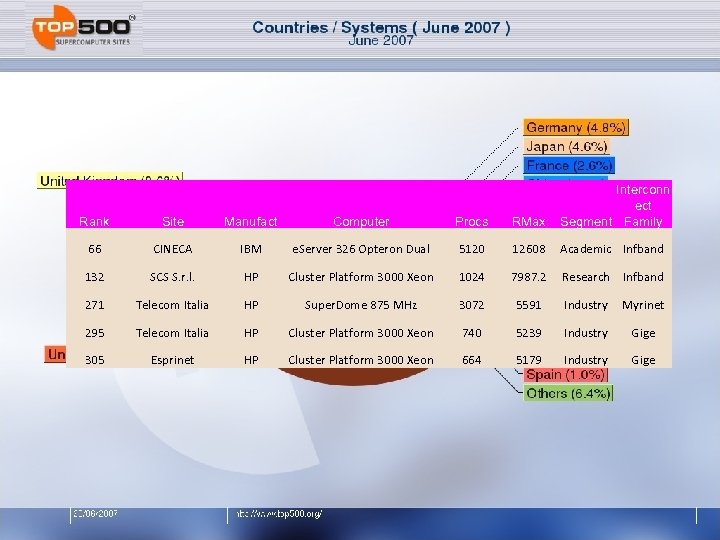Countries / Systems Rank Site Manufact Computer Procs RMax Interconn ect Segment Family 66 CINECA IBM e. Server 326 Opteron Dual 5120 12608 Academic Infband 132 SCS S. r. l. HP Cluster Platform 3000 Xeon 1024 7987. 2 Research Infband 271 Telecom Italia HP Super. Dome 875 MHz 3072 5591 Industry Myrinet 295 Telecom Italia HP Cluster Platform 3000 Xeon 740 5239 Industry Gige 305 Esprinet HP Cluster Platform 3000 Xeon 664 5179 Industry Gige www. top 500. o 29 th List / June 2007 page 11

Power is an Industry Wide Problem ¨ Google facilities Ø leveraging “Hiding in Plain Sight, Google Seeks More Power”, by John Markoff, June 14, 2006 hydroelectric power Ø old aluminum plants Ø >500, 000 servers worldwide New Google Plant in The Dulles, Oregon, from NYT, June 14, 2006 12

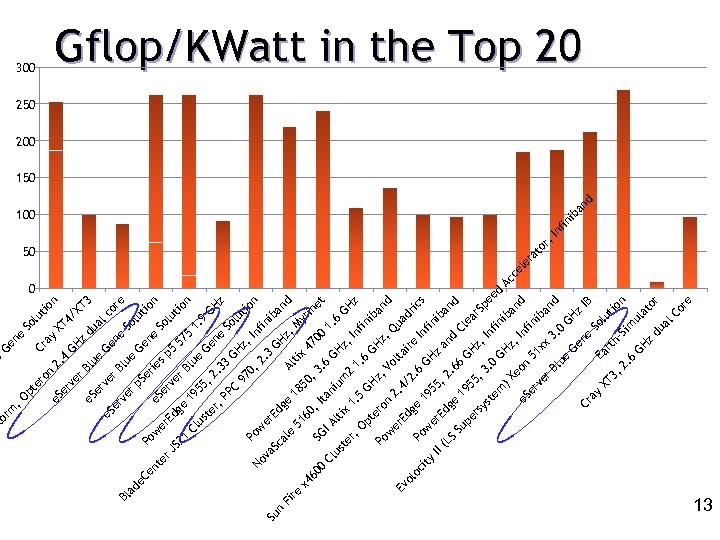21 JS ge Ed er w Po er B 57 lu So 3 n tio re co lu So al XT n tio 4/ XT lu So du ne Ge 5 z ne Ge GH ay Cr ne Ge sp e lu er ie p. S er v e. S er er B e lu er B 2. 4 e 100 50 0 tio n 5 19 lu Cl 1. e 55 us 9 Ge , 2 te GH ne r, . 3 z PP 3 GH Sol C ut 97 z, io Po 0, In n No w fin 2. er va 3 Su Ed Sc GH iba n nd ge al z, Fi Al e re 18 tix M 51 yr 50 x 4 60 47 in , 3 60 , I et 00 SG 0. 6 ta IA 1. Cl ni 6 us lti um GHz GH te x , I 2 1. r, z nf 1 5 Op in GH. 6 G ib te Hz a z, Po ro , Q nd n Vo w 2. er lta ua Ev 4/ Ed dr ire ol 2. ge ic oc Po 6 s 19 ity GH Infi w 55 ni er z II ba Ed , 2 an (L nd ge. 6 S d Su 6 Cl 19 GH pe ea 55 rs r. S z, , 3 ys p In. 0 te fin eed m GH ib Ac )X z, an ce eo In d e. S le n fin ra er 51 ib to ve xx an r, r. B 3. d In lu 0 fin e GH ib Ge z an ne Cr IB d ay So Ea lu XT rt tio 3, hn Si 2. m 6 ul GH at z or du al Co re er e. C en t ad Bl er v e. S n ro pt e , O m or St 300 Gflop/KWatt in the Top 20 250 200 150 13

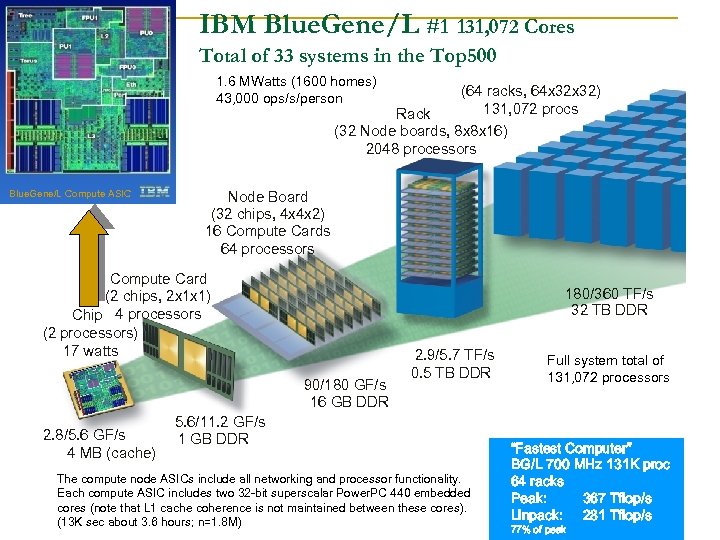IBM Blue. Gene/L #1 131, 072 Cores Total of 33 systems in the Top 500 1. 6 MWatts (1600 homes) 43, 000 ops/s/person (64 racks, 64 x 32) 131, 072 procs Rack (32 Node boards, 8 x 8 x 16) 2048 processors Blue. Gene/L Compute ASIC Node Board (32 chips, 4 x 4 x 2) 16 Compute Cards 64 processors Compute Card (2 chips, 2 x 1 x 1) Chip 4 processors (2 processors) 17 watts 180/360 TF/s 32 TB DDR 90/180 GF/s 16 GB DDR 2. 8/5. 6 GF/s 4 MB (cache) 2. 9/5. 7 TF/s 0. 5 TB DDR 5. 6/11. 2 GF/s 1 GB DDR The compute node ASICs include all networking and processor functionality. Each compute ASIC includes two 32 -bit superscalar Power. PC 440 embedded cores (note that L 1 cache coherence is not maintained between these cores). (13 K sec about 3. 6 hours; n=1. 8 M) Full system total of 131, 072 processors “Fastest Computer” BG/L 700 MHz 131 K proc 64 racks Peak: 367 Tflop/s Linpack: 281 Tflop/s 14 77% of peak

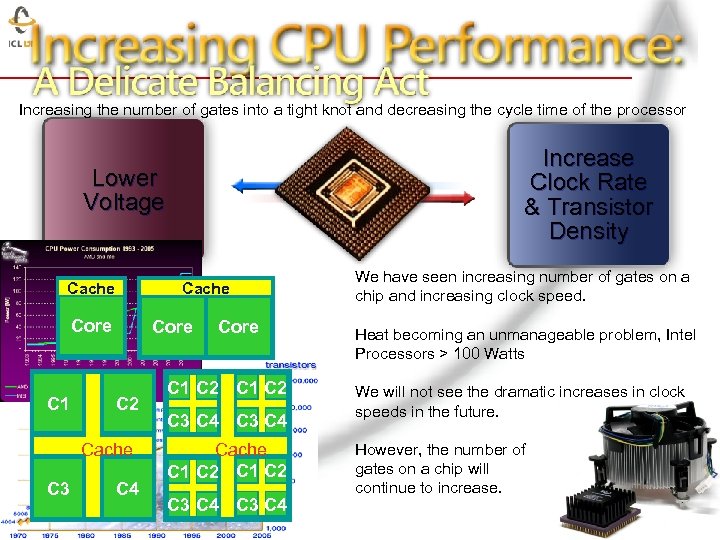Increasing the number of gates into a tight knot and decreasing the cycle time of the processor Increase Clock Rate & Transistor Density Lower Voltage Cache Core C 1 Core C 2 Cache C 3 C 4 Core We have seen increasing number of gates on a chip and increasing clock speed. Heat becoming an unmanageable problem, Intel Processors > 100 Watts C 1 C 2 C 3 C 4 We will not see the dramatic increases in clock speeds in the future. Cache C 1 C 2 C 3 C 4 However, the number of gates on a chip will continue to increase. 15

Power Cost of Frequency • Power ∝ Voltage 2 x Frequency (V 2 F) • Frequency ∝ Voltage • Power ∝Frequency 3 16

Power Cost of Frequency • Power ∝ Voltage 2 x Frequency (V 2 F) • Frequency ∝ Voltage • Power ∝Frequency 3 17

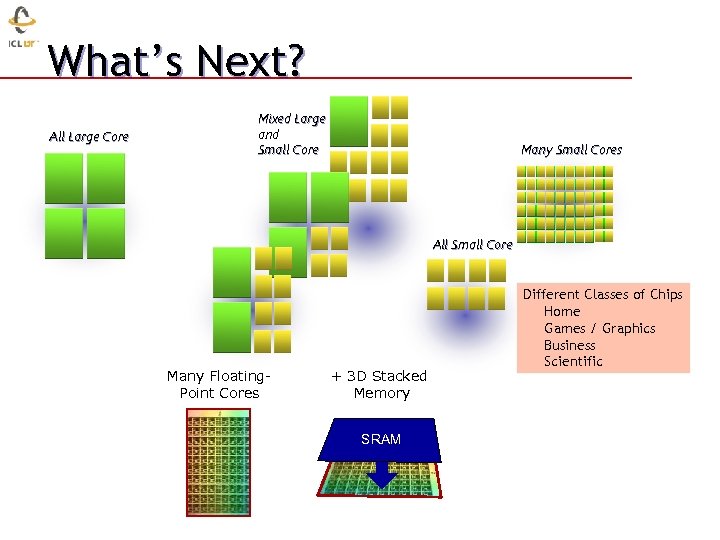What’s Next? All Large Core Mixed Large and Small Core Many Small Cores All Small Core Many Floating. Point Cores + 3 D Stacked Memory SRAM Different Classes of Chips Home Games / Graphics Business Scientific

Novel Opportunities in Multicores • Don’t have to contend with uniprocessors • Not your same old multiprocessor problem § How does going from Multiprocessors to Multicores impact programs? § What changed? § Where is the Impact? • Communication Bandwidth • Communication Latency 19

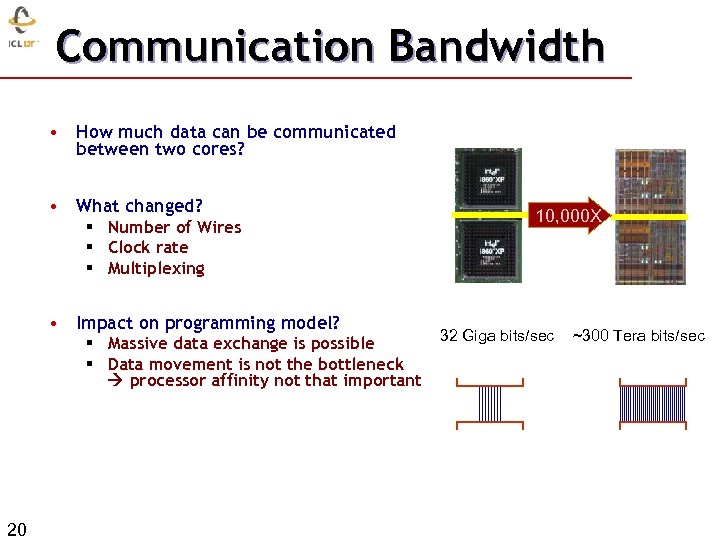Communication Bandwidth • How much data can be communicated between two cores? • What changed? § Number of Wires § Clock rate § Multiplexing • Impact on programming model? § Massive data exchange is possible § Data movement is not the bottleneck processor affinity not that important 20 10, 000 X 32 Giga bits/sec ~300 Tera bits/sec

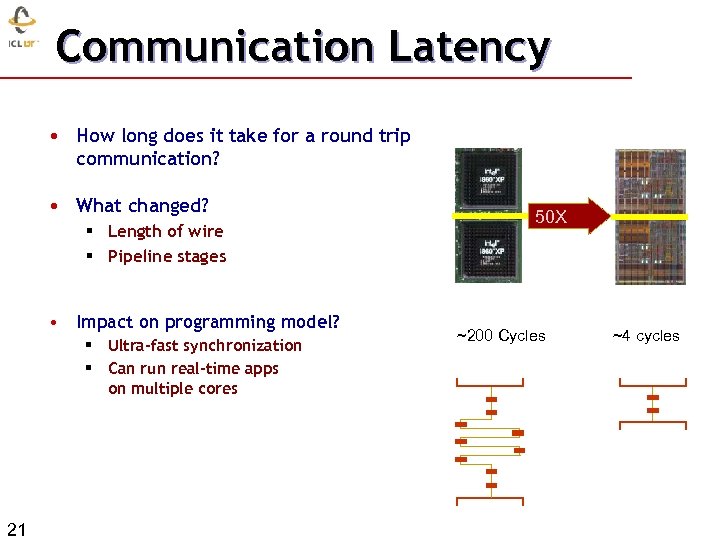Communication Latency • How long does it take for a round trip communication? • What changed? § Length of wire § Pipeline stages • Impact on programming model? § Ultra-fast synchronization § Can run real-time apps on multiple cores 21 50 X ~200 Cycles ~4 cycles

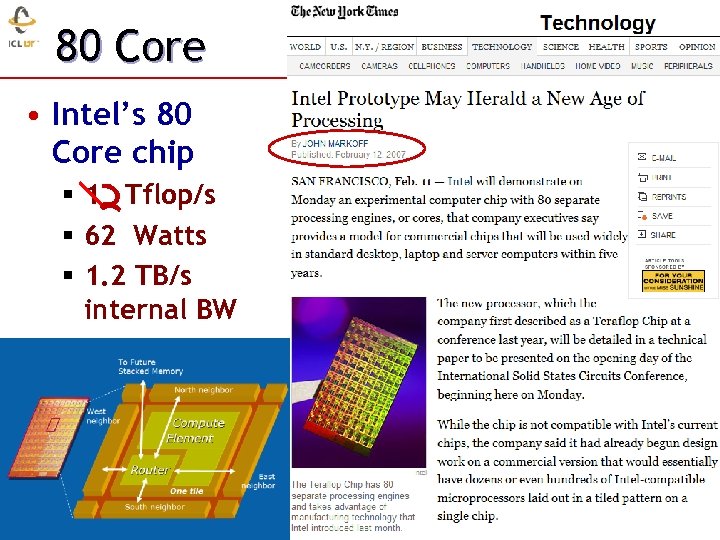80 Core • Intel’s 80 Core chip § 1 Tflop/s § 62 Watts § 1. 2 TB/s internal BW 22

NSF Track 1 – NCSA/UIUC • • $200 M 10 Pflop/s; 40 K 8 -core 4 Ghz IBM Power 7 chips; 1. 2 PB memory; 5 PB/s global bandwidth; interconnect BW of 0. 55 PB/s; 18 PB disk at 1. 8 TB/s I/O bandwidth. For use by a few people

NSF UTK/JICS Track 2 proposal • $65 M over 5 years for a 1 Pflop/s system § $30 M over 5 years for equipment • 36 cabinets of a Cray XT 5 • (AMD 8 -core/chip, 12 socket/board, 3 GHz, 4 flops/cycle/core) § $35 M over 5 years for operations • Power cost: • $1. 1 M/year • Cray Maintenance: • $1 M/year • To be used by the NSF community § 1000’s of users • Joins UCSD, PSC, TACC

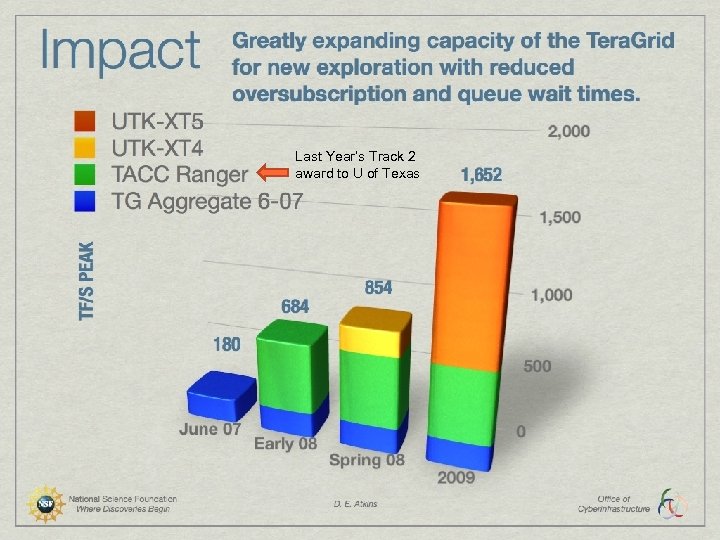Last Year’s Track 2 award to U of Texas

Major Changes to Software • Must rethink the design of our software § Another disruptive technology • Similar to what happened with cluster computing and message passing § Rethink and rewrite the applications, algorithms, and software • Numerical libraries for example will change § For example, both LAPACK and Sca. LAPACK will undergo major changes to accommodate this 27

Major Changes to Software • Must rethink the design of our software § Another disruptive technology • Similar to what happened with cluster computing and message passing § Rethink and rewrite the applications, algorithms, and software • Numerical libraries for example will change § For example, both LAPACK and Sca. LAPACK will undergo major changes to accommodate this 28

A New Generation of Software: Algorithms follow hardware evolution in time LINPACK (80’s) (Vector operations) Rely on - Level-1 BLAS operations LAPACK (90’s) (Blocking, cache friendly) Rely on - Level-3 BLAS operations PLASMA (00’s) New Algorithms (many-core friendly) Rely on - a DAG/scheduler - block data layout - some extra kernels Those new algorithms - have a very low granularity, they scale very well (multicore, petascale computing, … ) - removes a lots of dependencies among the tasks, (multicore, distributed computing) - avoid latency (distributed computing, out-of-core) - rely on fast kernels Those new algorithms need new kernels and rely on efficient scheduling algorithms.

A New Generation of Software: Parallel Linear Algebra Software for Multicore Architectures (PLASMA) Algorithms follow hardware evolution in time LINPACK (80’s) (Vector operations) Rely on - Level-1 BLAS operations LAPACK (90’s) (Blocking, cache friendly) Rely on - Level-3 BLAS operations PLASMA (00’s) New Algorithms (many-core friendly) Rely on - a DAG/scheduler - block data layout - some extra kernels Those new algorithms - have a very low granularity, they scale very well (multicore, petascale computing, … ) - removes a lots of dependencies among the tasks, (multicore, distributed computing) - avoid latency (distributed computing, out-of-core) - rely on fast kernels Those new algorithms need new kernels and rely on efficient scheduling algorithms.

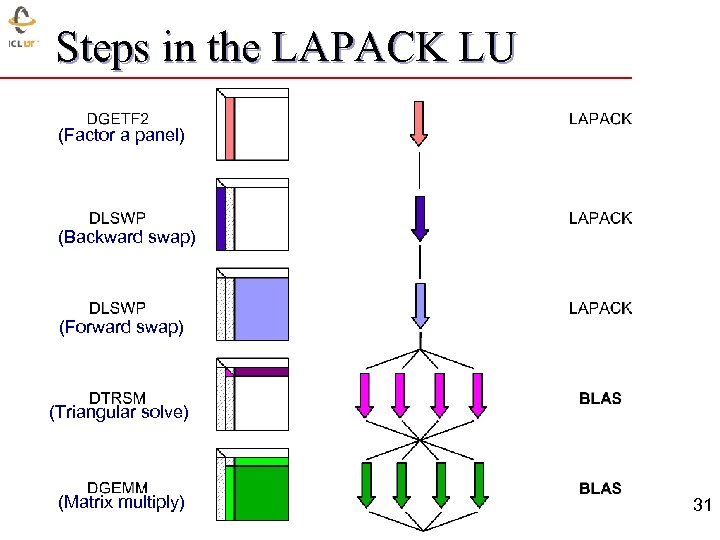Steps in the LAPACK LU (Factor a panel) (Backward swap) (Forward swap) (Triangular solve) (Matrix multiply) 31

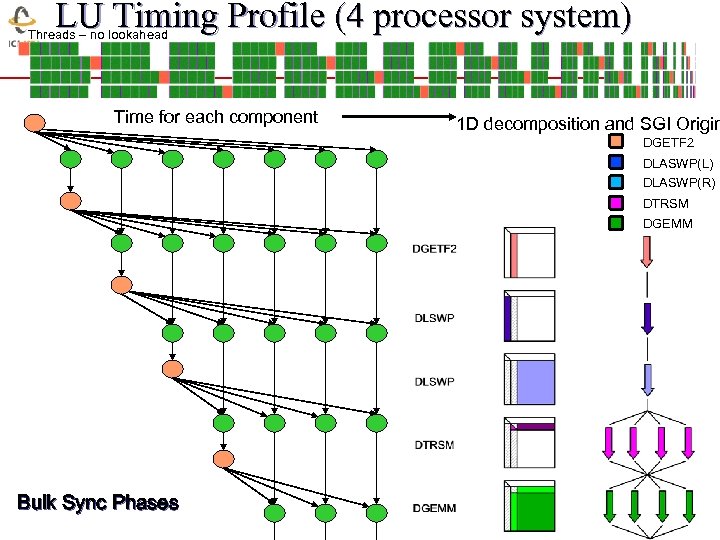LU Timing Profile (4 processor system) Threads – no lookahead Time for each component 1 D decomposition and SGI Origin DGETF 2 DLASWP(L) DLASWP(R) DTRSM DGEMM Bulk Sync Phases

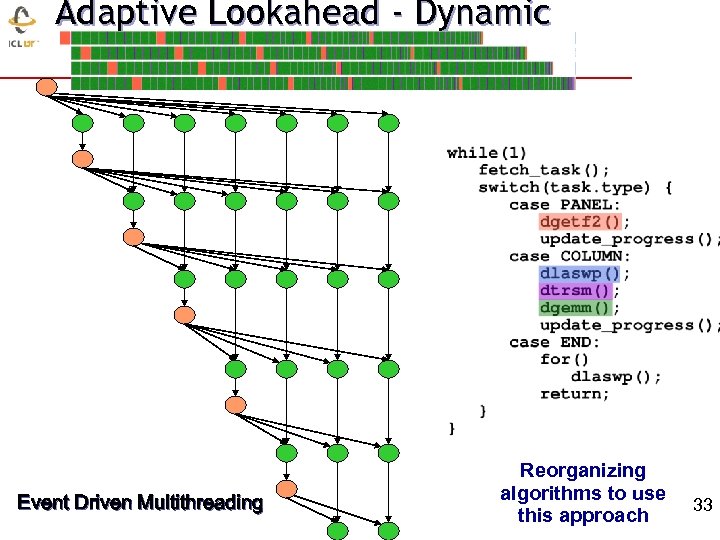Adaptive Lookahead - Dynamic Event Driven Multithreading Reorganizing algorithms to use this approach 33

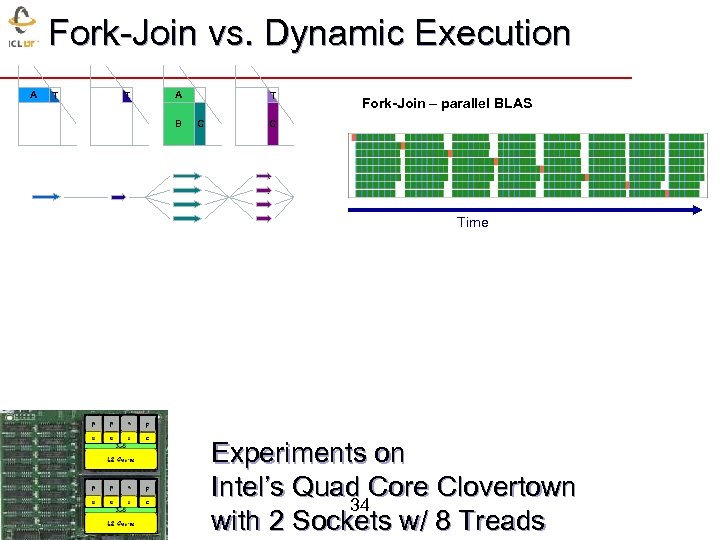Fork-Join vs. Dynamic Execution A T T A B T C Fork-Join – parallel BLAS C Time Experiments on Intel’s Quad Core Clovertown 34 with 2 Sockets w/ 8 Treads

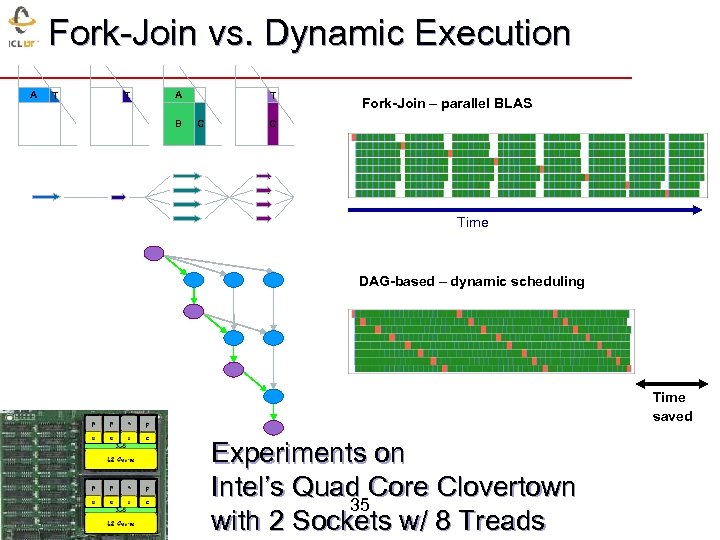Fork-Join vs. Dynamic Execution A T T A B T C Fork-Join – parallel BLAS C Time DAG-based – dynamic scheduling Time saved Experiments on Intel’s Quad Core Clovertown 35 with 2 Sockets w/ 8 Treads

With the Hype on Cell & PS 3 We Became Interested • The Play. Station 3's CPU based on a "Cell“ processor • Each Cell contains a Power PC processor and 8 SPEs. (SPE is processing unit, SPE: SPU + DMA engine) § An SPE is a self contained vector processor which acts independently from the others. • 4 way SIMD floating point units capable of a total of 25. 6 Gflop/s @ 3. 2 GHZ § 204. 8 Gflop/s peak! § The catch is that this is for 32 bit floating point; (Single Precision SP) § And 64 bit floating point runs at 14. 6 Gflop/s total for all 8 SPEs!! • Divide SP peak by 14; factor of 2 because of DP and 7 because of latency issues SPE ~ 25 Gflop/s peak 36

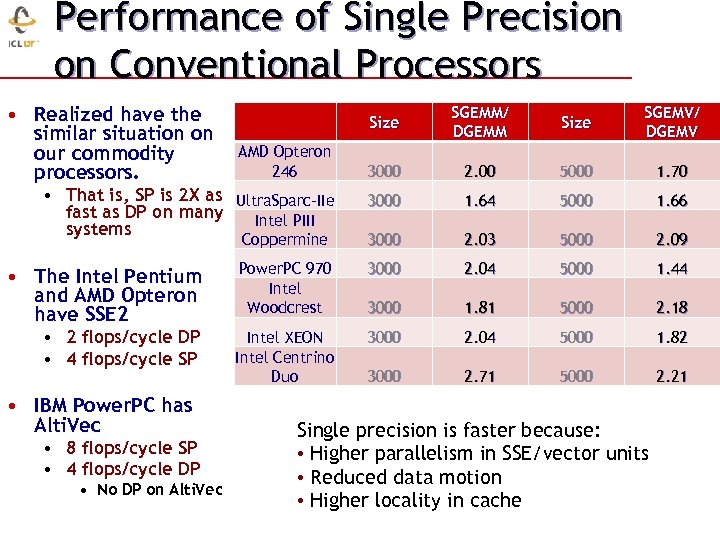Performance of Single Precision on Conventional Processors • Realized have the similar situation on our commodity processors. Size SGEMM/ DGEMM Size SGEMV/ DGEMV AMD Opteron 246 3000 2. 00 5000 1. 70 • That is, SP is 2 X as Ultra. Sparc-IIe fast as DP on many Intel PIII systems 3000 1. 64 5000 1. 66 Coppermine 3000 2. 03 5000 2. 09 • The Intel Pentium and AMD Opteron have SSE 2 Power. PC 970 Intel Woodcrest 3000 2. 04 5000 1. 44 3000 1. 81 5000 2. 18 • 2 flops/cycle DP • 4 flops/cycle SP Intel XEON Intel Centrino Duo 3000 2. 04 5000 1. 82 3000 2. 71 5000 2. 21 • IBM Power. PC has Alti. Vec • 8 flops/cycle SP • 4 flops/cycle DP • No DP on Alti. Vec Single precision is faster because: • Higher parallelism in SSE/vector units • Reduced data motion • Higher locality in cache

32 or 64 bit Floating Point Precision? • A long time ago 32 bit floating point was used § Still used in scientific apps but limited • Most apps use 64 bit floating point § Accumulation of round off error • A 10 TFlop/s computer running for 4 hours performs > 1 Exaflop (1018) ops. § Ill conditioned problems § IEEE SP exponent bits too few (8 bits, 10± 38) § Critical sections need higher precision • Sometimes need extended precision (128 bit fl pt) § However some can get by with 32 bit fl pt in some parts • Mixed precision a possibility § Approximate in lower precision and then refine or improve solution to high precision. 38

Idea Goes Something Like This… • Exploit 32 bit floating point as much as possible. § Especially for the bulk of the computation • Correct or update the solution with selective use of 64 bit floating point to provide a refined results • Intuitively: § Compute a 32 bit result, § Calculate a correction to 32 bit result using selected higher precision and, § Perform the update of the 32 bit results with the correction using high precision. 39

Mixed-Precision Iterative Refinement • Iterative refinement for dense systems, Ax = b, can work this way. L U = lu(A) x = L(Ub) O(n 3) SINGLE r = b – Ax DOUBLE O(n 2) WHILE || r || not small enough z = L(Ur) x=x+z DOUBLE r = b – Ax END SINGLE DOUBLE O(n 2) O(n 1) O(n 2)

Mixed-Precision Iterative Refinement • Iterative refinement for dense systems, Ax = b, can work this way. L U = lu(A) x = L(Ub) O(n 3) SINGLE r = b – Ax DOUBLE O(n 2) WHILE || r || not small enough z = L(Ur) SINGLE x=x+z DOUBLE r = b – Ax DOUBLE O(n 2) O(n 1) O(n 2) END § Wilkinson, Moler, Stewart, & Higham provide error bound for SP fl pt results when using DP fl pt. § It can be shown that using this approach we can compute the solution to 64 -bit floating point precision. • Requires extra storage, total is 1. 5 times normal; • O(n 3) work is done in lower precision • O(n 2) work is done in high precision • Problems if the matrix is ill-conditioned in sp; O(108)

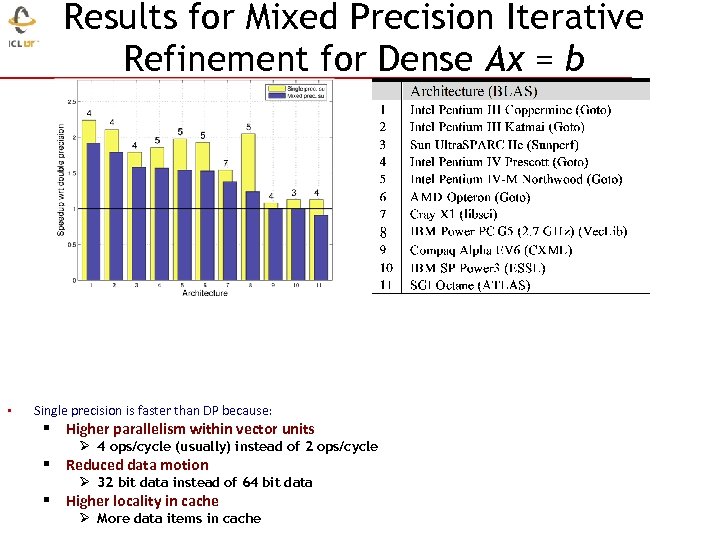Results for Mixed Precision Iterative Refinement for Dense Ax = b • Single precision is faster than DP because: § Higher parallelism within vector units Ø 4 ops/cycle (usually) instead of 2 ops/cycle § Reduced data motion Ø 32 bit data instead of 64 bit data § Higher locality in cache Ø More data items in cache

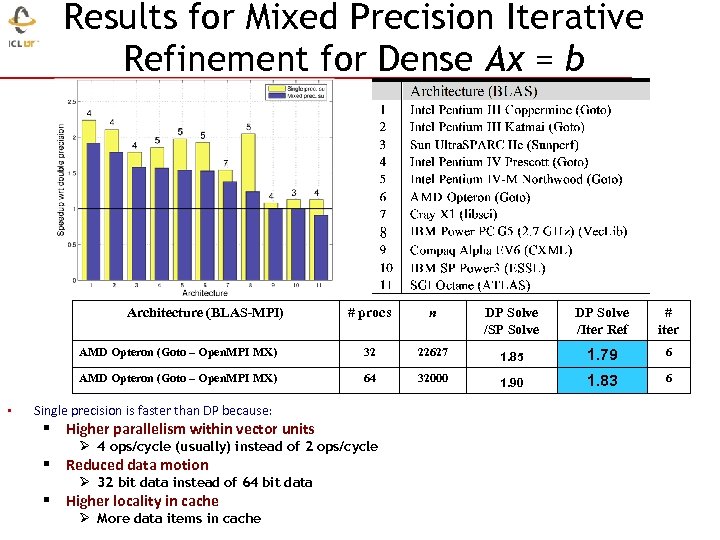Results for Mixed Precision Iterative Refinement for Dense Ax = b Architecture (BLAS-MPI) n DP Solve /SP Solve DP Solve /Iter Ref # iter AMD Opteron (Goto – Open. MPI MX) 32 22627 1. 85 1. 79 6 AMD Opteron (Goto – Open. MPI MX) • # procs 64 32000 1. 90 1. 83 6 Single precision is faster than DP because: § Higher parallelism within vector units Ø 4 ops/cycle (usually) instead of 2 ops/cycle § Reduced data motion Ø 32 bit data instead of 64 bit data § Higher locality in cache Ø More data items in cache

What about the Cell? • Power PC at 3. 2 GHz § DGEMM at 5 Gflop/s § Altivec peak at 25. 6 Gflop/s • Achieved 10 Gflop/s SGEMM • 8 SPUs § 204. 8 Gflop/s peak! § The catch is that this is for 32 bit floating point; (Single Precision SP) § And 64 bit floating point runs at 14. 6 Gflop/s total for all 8 SPEs!! • Divide SP peak by 14; factor of 2 because of DP and 7 because of latency issues 44

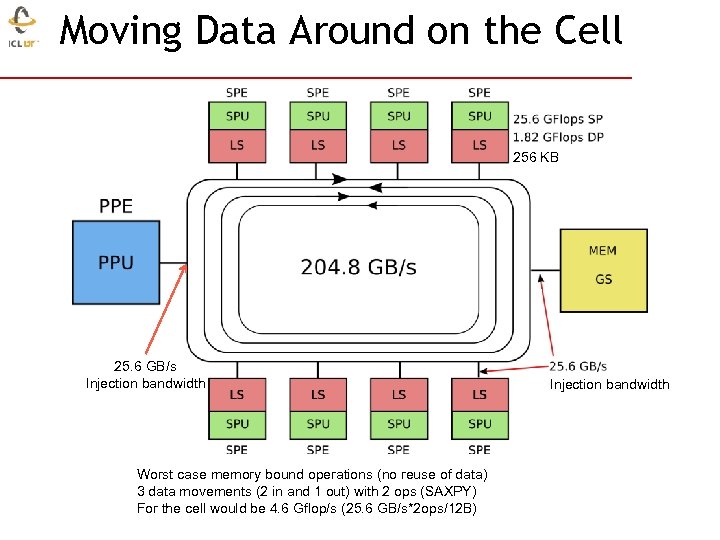Moving Data Around on the Cell 256 KB 25. 6 GB/s Injection bandwidth Worst case memory bound operations (no reuse of data) 3 data movements (2 in and 1 out) with 2 ops (SAXPY) For the cell would be 4. 6 Gflop/s (25. 6 GB/s*2 ops/12 B) Injection bandwidth

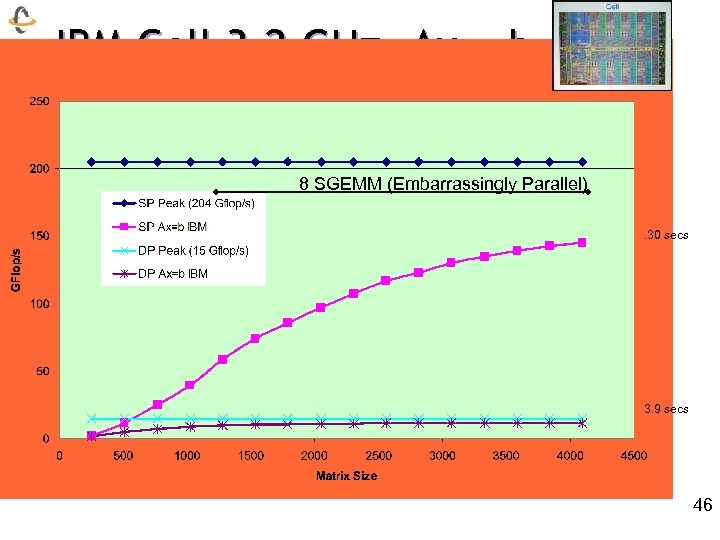IBM Cell 3. 2 GHz, Ax = b 8 SGEMM (Embarrassingly Parallel). 30 secs 3. 9 secs 46

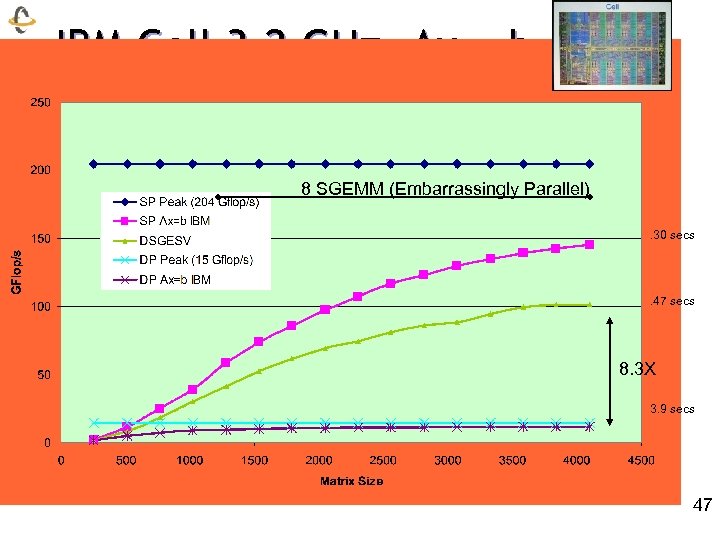IBM Cell 3. 2 GHz, Ax = b 8 SGEMM (Embarrassingly Parallel). 30 secs . 47 secs 8. 3 X 3. 9 secs 47

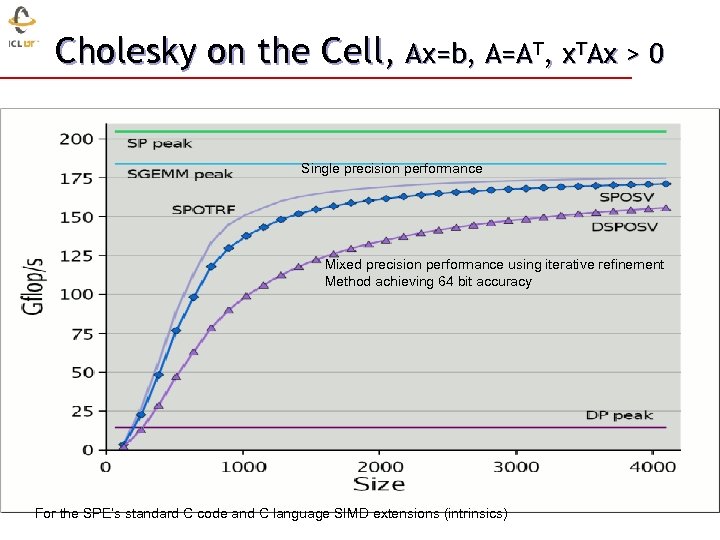Cholesky on the Cell, Ax=b, A=AT, x. TAx > 0 Single precision performance Mixed precision performance using iterative refinement Method achieving 64 bit accuracy 33 For the SPE’s standard C code and C language SIMD extensions (intrinsics) 48

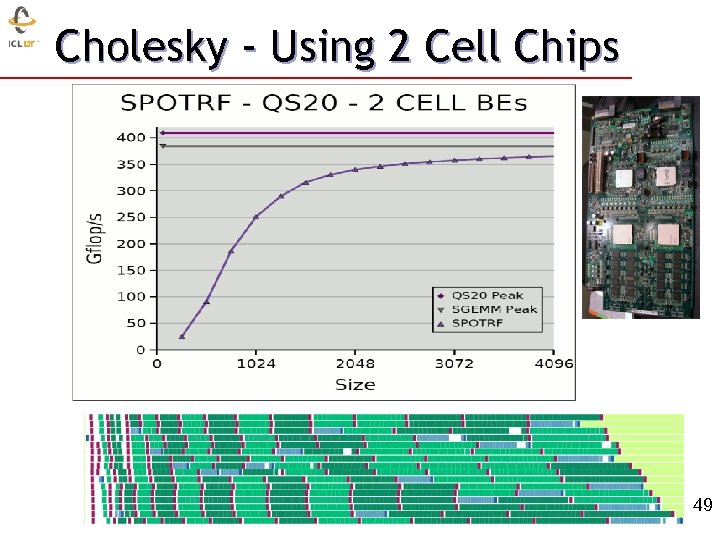Cholesky - Using 2 Cell Chips 49

Intriguing Potential • Exploit lower precision as much as possible § Payoff in performance • Faster floating point • Less data to move • Automatically switch between SP and DP to match the desired accuracy § Compute solution in SP and then a correction to the solution in DP • Potential for GPU, FPGA, special purpose processors § What about 16 bit floating point? • Use as little you can get away with and improve the accuracy • Applies to sparse direct and iterative linear systems and Eigenvalue, optimization problems, where Newton’s method is used. 50 Correction = - A(b – Ax)

IBM/Mercury Cell Blade ¨ From IBM or Mercury Ø 2 Cell chip Ø Each w/8 SPEs Ø 512 MB/Cell Ø ~$8 K - 17 K Ø Some SW 33 51

Sony Playstation 3 Cluster PS 3 -T ¨ From IBM or Mercury Ø 2 Cell chip Ø Each w/8 SPEs Ø 512 MB/Cell Ø ~$8 K - 17 K Ø Some SW ¨ From WAL*MART PS 3 Ø 1 Cell chip Ø w/6 SPEs Ø Ø 256 MB/PS 3 $600 Download SW Dual boot 33 52

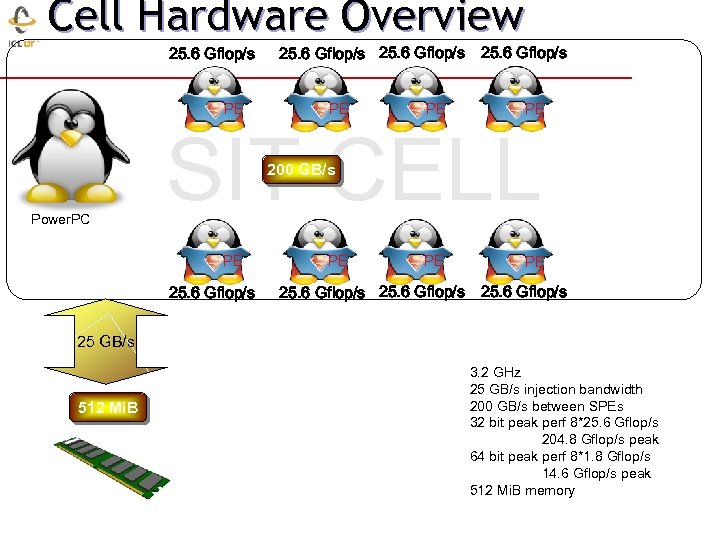Cell Hardware Overview 25. 6 Gflop/s PE 25. 6 Gflop/s PE PE PE SIT CELL 200 GB/s Power. PC PE 25. 6 Gflop/s PE PE PE 25. 6 Gflop/s 25 GB/s 512 Mi. B 3. 2 GHz 25 GB/s injection bandwidth 200 GB/s between SPEs 32 bit peak perf 8*25. 6 Gflop/s 204. 8 Gflop/s peak 64 bit peak perf 8*1. 8 Gflop/s 14. 6 Gflop/s peak 512 Mi. B memory

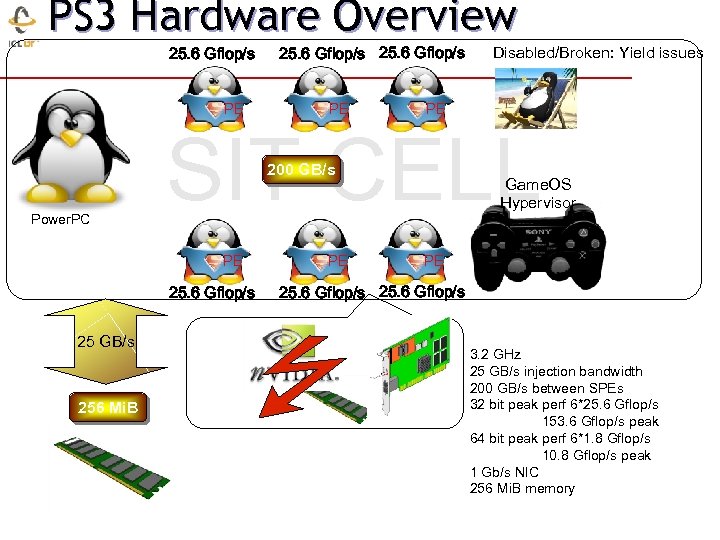PS 3 Hardware Overview 25. 6 Gflop/s PE PE SIT CELL 200 GB/s Power. PC PE 25. 6 Gflop/s 25 GB/s 256 Mi. B Disabled/Broken: Yield issues PE Game. OS Hypervisor PE 25. 6 Gflop/s 3. 2 GHz 25 GB/s injection bandwidth 200 GB/s between SPEs 32 bit peak perf 6*25. 6 Gflop/s 153. 6 Gflop/s peak 64 bit peak perf 6*1. 8 Gflop/s 10. 8 Gflop/s peak 1 Gb/s NIC 256 Mi. B memory

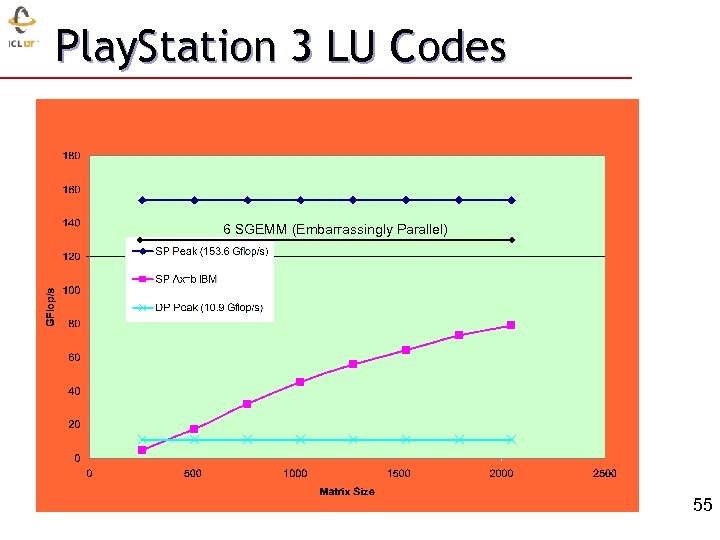Play. Station 3 LU Codes 6 SGEMM (Embarrassingly Parallel) 33 55

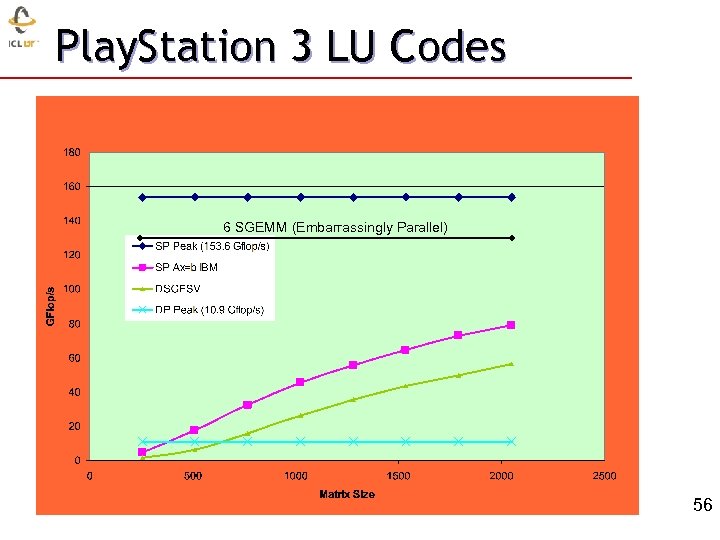Play. Station 3 LU Codes 6 SGEMM (Embarrassingly Parallel) 33 56

Cholesky on the PS 3, Ax=b, A=AT, x. TAx > 0 33 57

HPC in the Living Room 33 58

Matrix Multiple on a 4 Node Play. Station 3 Cluster What's bad What's good Gigabit network card. 1 Gb/s is too little for such computational power (150 Gflop/s per node) Linux can only run on top of Game. OS (hypervisor) Extremely high network access latencies (120 usec) Low bandwidth (600 Mb/s) Only 256 MB local memory Only 6 SPEs Very cheap: ~4$ per Gflop/s (with 32 bit fl pt theoretical peak) Fast local computations between SPEs Perfect overlap between communications and computations is possible (Open-MPI running): PPE does communication via MPI SPEs do computation via SGEMMs 33 Gold: Computation: 8 ms Blue: Communication: 20 ms

Users Guide for SC on PS 3 • SCOP 3: A Rough Guide to Scientific Computing on the Play. Station 3 • See webpage for details 33

Conclusions • For the last decade or more, the research investment strategy has been overwhelmingly biased in favor of hardware. • This strategy needs to be rebalanced barriers to progress are increasingly on the software side. • Moreover, the return on investment is more favorable to software. § Hardware has a half-life measured in years, while software has a half-life measured in decades. • High Performance Ecosystem out of balance § Hardware, OS, Compilers, Software, Algorithms, Applications • No Moore’s Law for software, algorithms and applications

Collaborators / Support Alfredo Buttari, UTK Julien Langou, UColorado Julie Langou, UTK Piotr Luszczek, Math. Works Jakub Kurzak, UTK Stan Tomov, UTK 33