An Inverse BEM GA Approach to Determining Heat Transfer

An Inverse BEM/GA Approach to Determining Heat Transfer Coefficient Distributions Within Film Cooling Holes/Slots Mahmood Silieti Eduardo Divo Alain Kassab Mechanical, Materials, and Aerospace Engineering Department University of Central Florida, Orlando, FL, USA IPE 2003 Tuscaloosa, Alabama 1

Overview: • Motivation • Procedure • Problem Setup • Conjugate Heat Transfer Solution • Direct BEM Conduction Solution/Verification • Inverse Problem and Objective Function • Optimization Technique: Genetic Algorithms • Numerical Results • Conclusions and Extensions IPE 2003 Tuscaloosa, Alabama 2

Motivation: Find end Wall Film Cooling Effectiveness and heat transfer coefficients (HTC) Can measure film effectiveness using optical thermography: which also provides To define endwall HTC. IPE 2003 Tuscaloosa, Alabama 3

Closed loop Transonic Test Rig at UCF funded by SWPC IPE 2003 Tuscaloosa, Alabama 4

To find endwall HTC: will solve 3 D inverse conduction problem using endwall temperature measurements, however, HTC in film hole is unknown? There are 10 types of film cooling holes in this experiment, several of these are shaped and all are inclined. Objective of this feasibility study is to find a means of determining HTC correlation in film hole to be used in later 3 D inverse problem analysis for endwall HTC Each type of film cooling hole is subject of a single hole calibration Experiment that will yield to be used in correlation IPE 2003 Tuscaloosa, Alabama 5

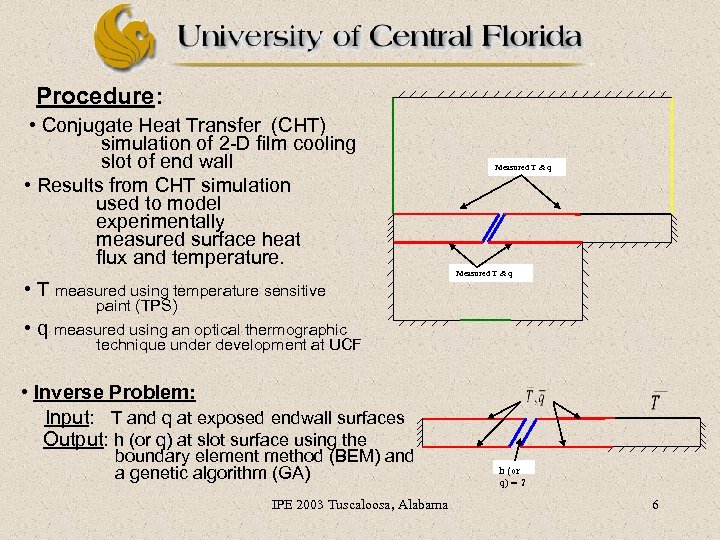
Procedure: • Conjugate Heat Transfer (CHT) simulation of 2 -D film cooling slot of end wall • Results from CHT simulation used to model experimentally measured surface heat flux and temperature. Measured T & q • T measured using temperature sensitive • q paint (TPS) measured using an optical thermographic technique under development at UCF • Inverse Problem: Input: T and q at exposed endwall surfaces Output: h (or q) at slot surface using the boundary element method (BEM) and a genetic algorithm (GA) IPE 2003 Tuscaloosa, Alabama h (or q) = ? 6

Setup for CHT Simulation: 2 -D Film Cooling Slot IPE 2003 Tuscaloosa, Alabama 7

Mesh has been created using Gambit (FLUENT grid generator) Fluid Grid Nodes=41, 112 Solid Grid Nodes=2, 104 IPE 2003 Tuscaloosa, Alabama 8

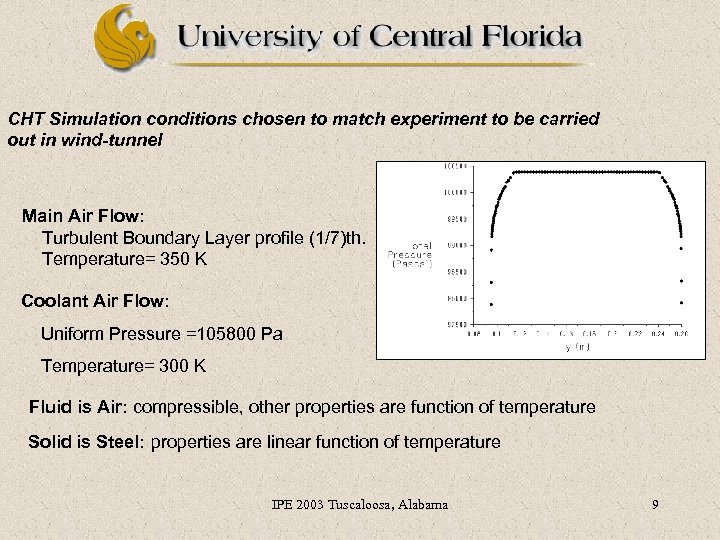
CHT Simulation conditions chosen to match experiment to be carried out in wind-tunnel Main Air Flow: Turbulent Boundary Layer profile (1/7)th. Temperature= 350 K Coolant Air Flow: Uniform Pressure =105800 Pa Temperature= 300 K Fluid is Air: compressible, other properties are function of temperature Solid is Steel: properties are linear function of temperature IPE 2003 Tuscaloosa, Alabama 9

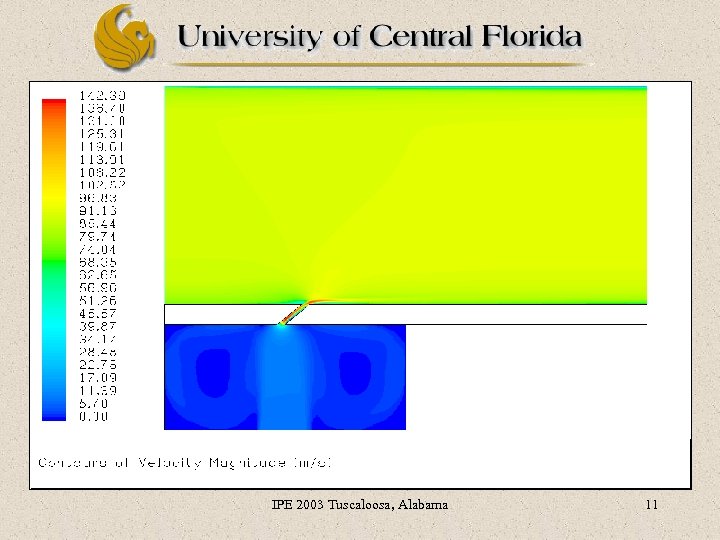
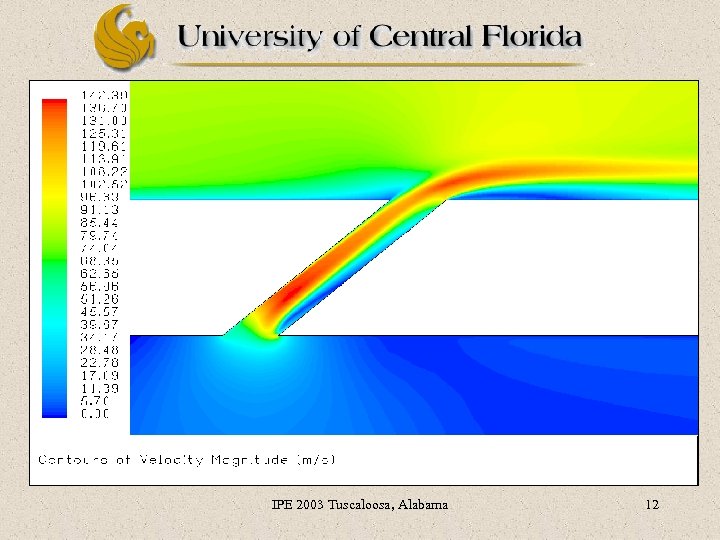
CHT Solver: Ø Commercial Code “Fluent” Finite Volume Ø Full Navier-Stokes Equation for compressible turbulent flow “RNG “ CHT Results: Ø Results are converged at least ( mass, momentum, energy, for all residuals & ) IPE 2003 Tuscaloosa, Alabama 10

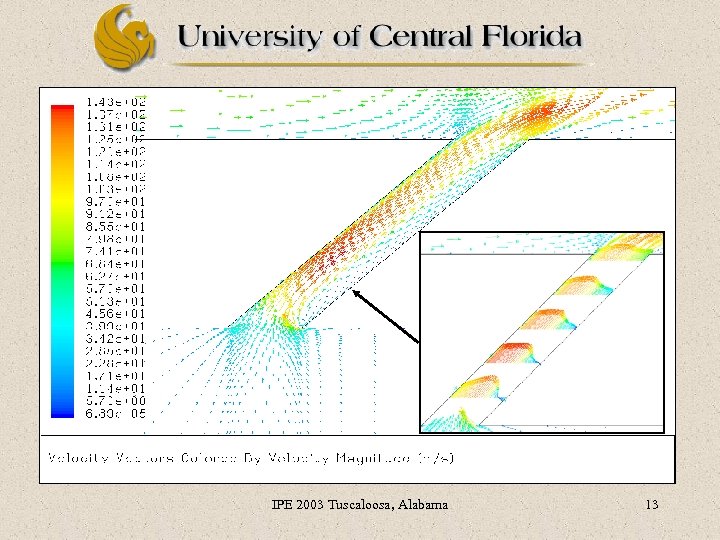
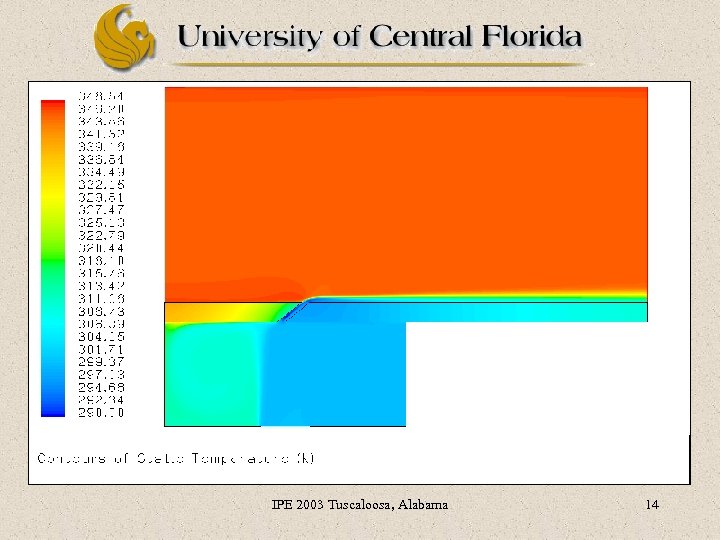
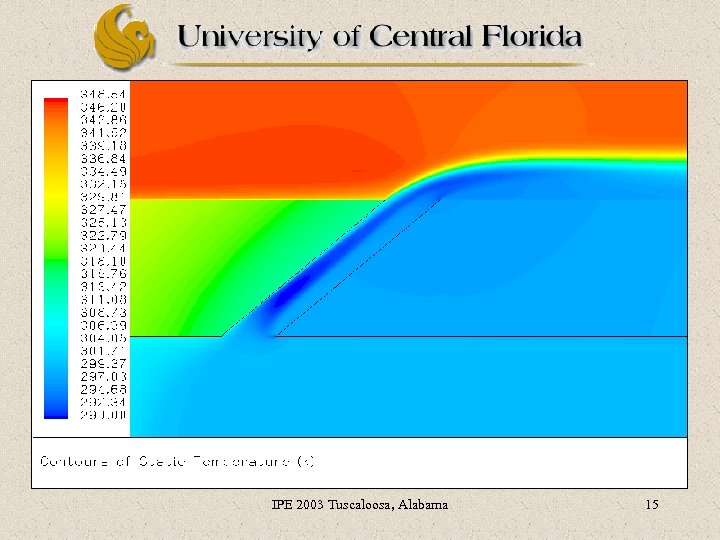
IPE 2003 Tuscaloosa, Alabama 11

IPE 2003 Tuscaloosa, Alabama 12

IPE 2003 Tuscaloosa, Alabama 13

IPE 2003 Tuscaloosa, Alabama 14

IPE 2003 Tuscaloosa, Alabama 15

Direct BEM Conduction Solution: Ø Numerical consistency check of BEM (in-house) and CHT (commercial) code. Ø BEM surface mesh and CHT surface mesh are different radial basis function (RBF) interpolation used to pass information from one grid to the other. Ø Input CHT wall temperatures at solid surfaces to BEM and check BEM computed heat fluxes. measured T IPE 2003 Tuscaloosa, Alabama 16

BEM Methodology Ø Surface Mesh only: (we use quadratic discontinuous elements) Ø Governing Equation: (Boundary Integral Equation for Laplace Eqn. ) Where: G(x, ) = (-1/ 2 k) ln r(x, ) in 2 D H(x, ) = -k G(x, ) / n IPE 2003 Tuscaloosa, Alabama q(x) = -k T(x) / n C( ) = 1 if C( ) = 1/2 if 17

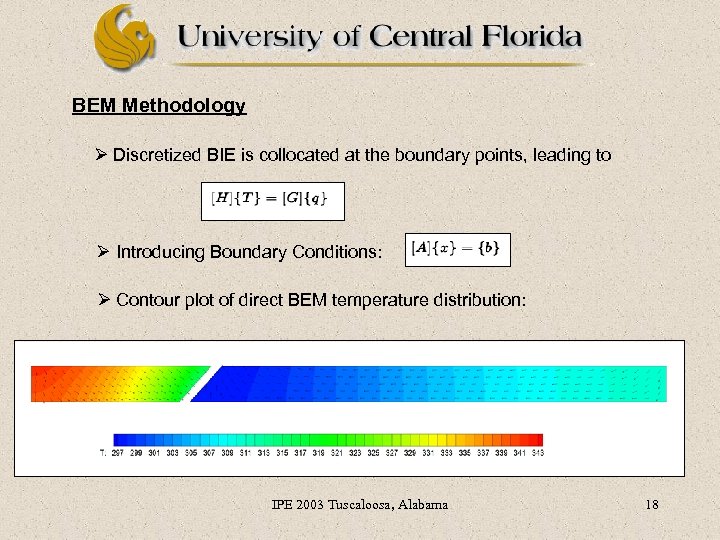
BEM Methodology Ø Discretized BIE is collocated at the boundary points, leading to Ø Introducing Boundary Conditions: Ø Contour plot of direct BEM temperature distribution: IPE 2003 Tuscaloosa, Alabama 18

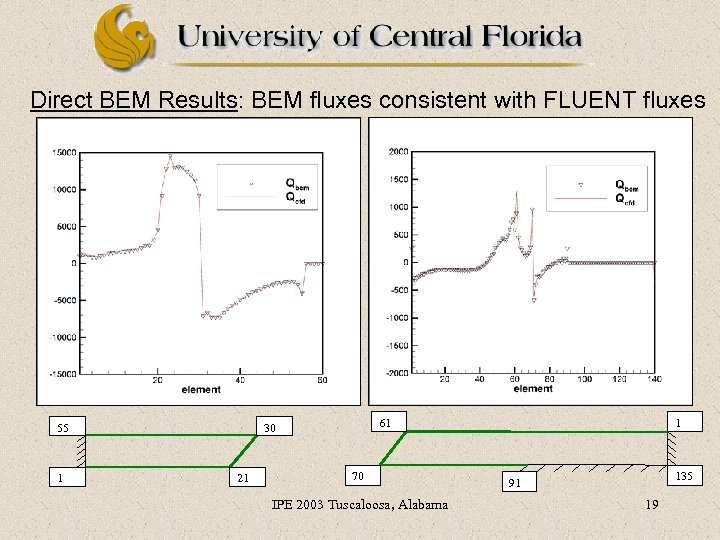
Direct BEM Results: BEM fluxes consistent with FLUENT fluxes 55 1 21 1 61 30 70 IPE 2003 Tuscaloosa, Alabama 135 91 19

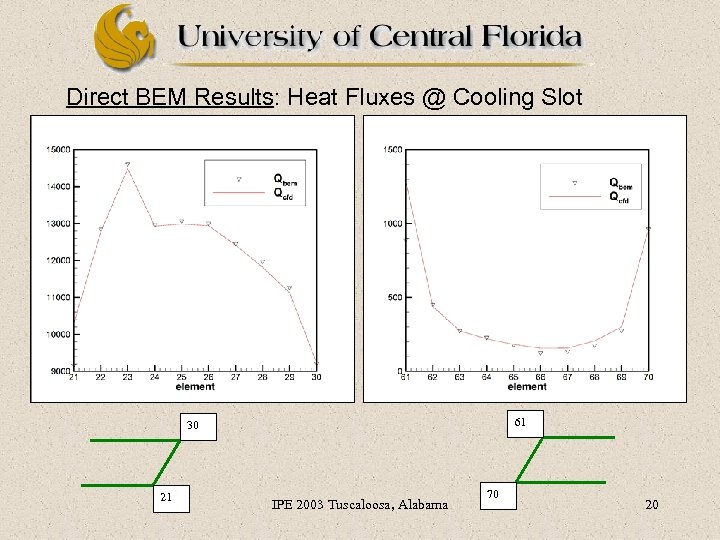
Direct BEM Results: Heat Fluxes @ Cooling Slot 61 30 21 IPE 2003 Tuscaloosa, Alabama 70 20

Inverse Problem: Ø Cauchy conditions (T and q) imposed at the surfaces exposed to hot and cold gases. Ø Both temperature and flux are unknown on the surfaces of the cooling slot. h (or q) = ? IPE 2003 Tuscaloosa, Alabama 21

Inverse Problem: Ø Identification of heat fluxes in the cooling slot to match over-specified boundary data at the exposed surfaces. Ø Parametric representation of heat flux in cooling slot using radial basis functions (RBF) Anchor point BEM node Ø Objective function is to minimize IPE 2003 Tuscaloosa, Alabama 22

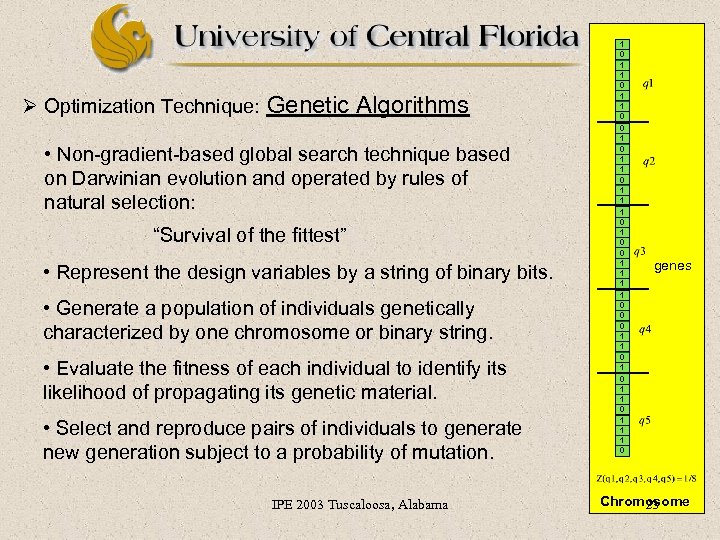
Ø Optimization Technique: Genetic Algorithms • Non-gradient-based global search technique based on Darwinian evolution and operated by rules of natural selection: “Survival of the fittest” • Represent the design variables by a string of binary bits. • Generate a population of individuals genetically characterized by one chromosome or binary string. • Evaluate the fitness of each individual to identify its likelihood of propagating its genetic material. • Select and reproduce pairs of individuals to generate new generation subject to a probability of mutation. IPE 2003 Tuscaloosa, Alabama 1 0 1 1 0 1 1 1 0 0 0 1 1 1 0 genes Chromosome 23

Optimization Technique: Advantages: Genetic Algorithms - Very robust - Almost guaranteed global optimal - Inherent regularization Disadvantage: - Very slow Solution: - Parallelize process in a Computer Cluster by assigning different individuals to different nodes in the cluster. (Very efficient parallelization as very little communication is necessary) IPE 2003 Tuscaloosa, Alabama 24

Optimization Technique: Parameters: Parallel Genetic Algorithms - population size = 50 - probability of jump mutation = 4% - probability of creep mutation = 20% - number of bits per parameter = 8 (255 steps) - number of children = 1 - ellitistic generation = 1 - parameter bound = searches for q between qmin and qmax block#1 (-15, 000 to 15, 000) block#2 (-2, 000 to 2, 000) IPE 2003 Tuscaloosa, Alabama 25

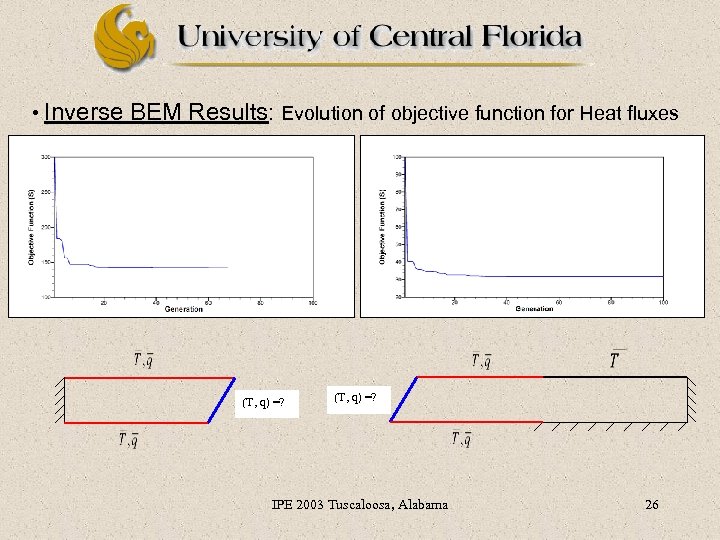
• Inverse BEM Results: Evolution of objective function for Heat fluxes (T, q) =? IPE 2003 Tuscaloosa, Alabama 26

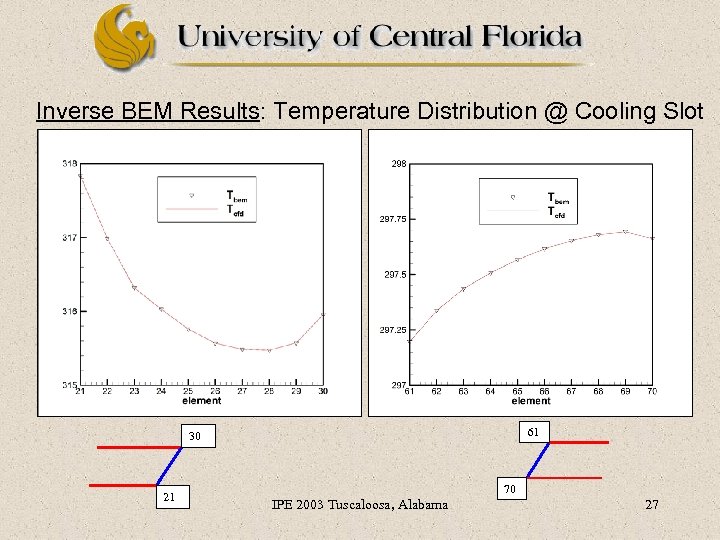
Inverse BEM Results: Temperature Distribution @ Cooling Slot 61 30 21 70 IPE 2003 Tuscaloosa, Alabama 27

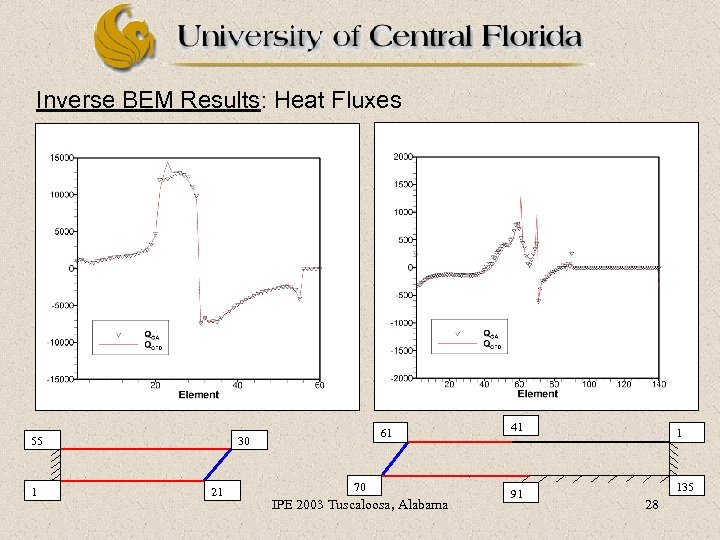
Inverse BEM Results: Heat Fluxes 55 1 61 30 21 70 IPE 2003 Tuscaloosa, Alabama 41 91 1 135 28

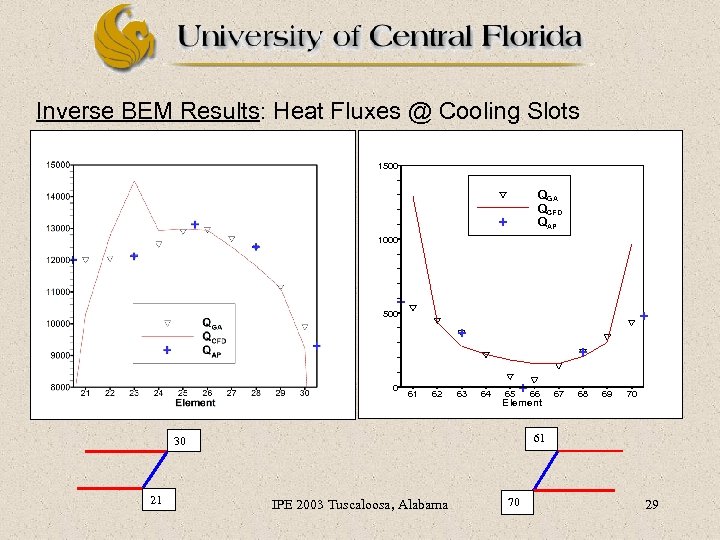
Inverse BEM Results: Heat Fluxes @ Cooling Slots 1500 QGA QCFD QAP + 1000 + + 500 + + 0 61 62 63 64 65 + 66 Element 68 69 70 61 30 21 67 IPE 2003 Tuscaloosa, Alabama 70 29

Conclusions and Extensions: • Methodology shows promise in predicting the temperature and the heat fluxes within the slot. • Add more anchor points to capture the changes in heat fluxes. Add a regularization term to reduce unwanted oscillations associated with more anchor points. • Need to study the effect of input error in temperature and heat flux on resolution. • Apply the methodology to multiple slots. • Apply the methodology to 3 -d single and multiple filmcooling holes. IPE 2003 Tuscaloosa, Alabama 30