6136b0fe5b537ebc03c91cb239d41601.ppt
- Количество слайдов: 42

An Introduction to X-Ray Diffraction by Single Crystals and Powders Patrick Mc. Ardle NUI, Galway, Ireland pma 2017

The Nature of Crystalline Materials • Crystalline materials differ from amorphous materials in that they have long range order. They also exhibit X-ray powder diffraction patterns. • Amorphous materials may have very short range order (e. g. molecular dimers) but do not have long range order and do not exhibit X-ray powder diffraction patterns. • The packing of atoms, molecules or ions within a crystal occurs in a symmetrical manner and furthermore this symmetrical arrangement is repetitive throughout a piece of crystalline material. • This repetitive arrangement forms a crystal lattice. A crystal lattice can be constructed as follows: pma 2017
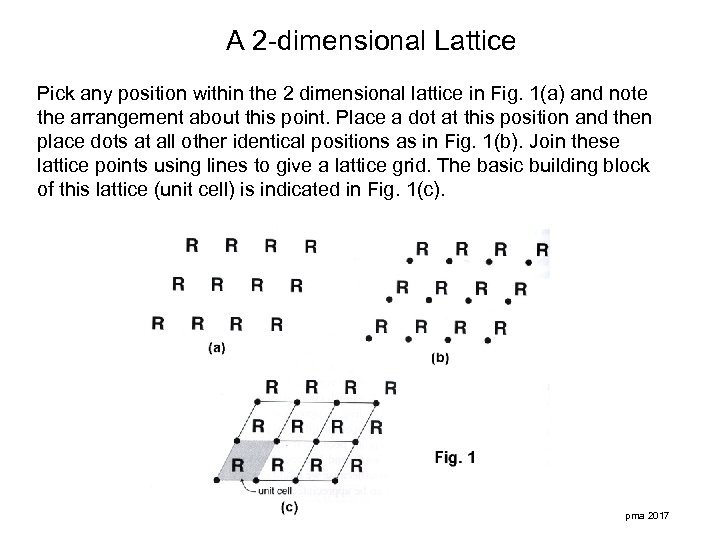
A 2 -dimensional Lattice Pick any position within the 2 dimensional lattice in Fig. 1(a) and note the arrangement about this point. Place a dot at this position and then place dots at all other identical positions as in Fig. 1(b). Join these lattice points using lines to give a lattice grid. The basic building block of this lattice (unit cell) is indicated in Fig. 1(c). pma 2017

Unit Cell Types and The Seven Crystal Systems Cubic Tetragonal Orthorhombic Monoclinic Triclinic Rhombohedral (or Trigonal) Hexagonal a = b = c. a = b c. a b c. . a = b = c. = = = 90º. = = = 90 º. = = 90º, 90º. = = 90 º. a = b c. = = 90º, = 120º. c b a Orthorhombic In general, six parameters are required to define the shape and size of a unit cell, these being three cell edge lengths (conventionally, defined as a, b, and c), and three angles (conventionally, defined as , , and ). In the strict mathematical sense, a, b, and c are vectors since they specify both length and direction. is the angle between b and c, is the angle between a and b. The unit cell should be right handed. Check the cell above with your right hand Unit Cells may centred on one or more faces or at the centre of the cell. When the unit cells listed above are combined with centring there are 14 different Bravais lattices. pma 2017
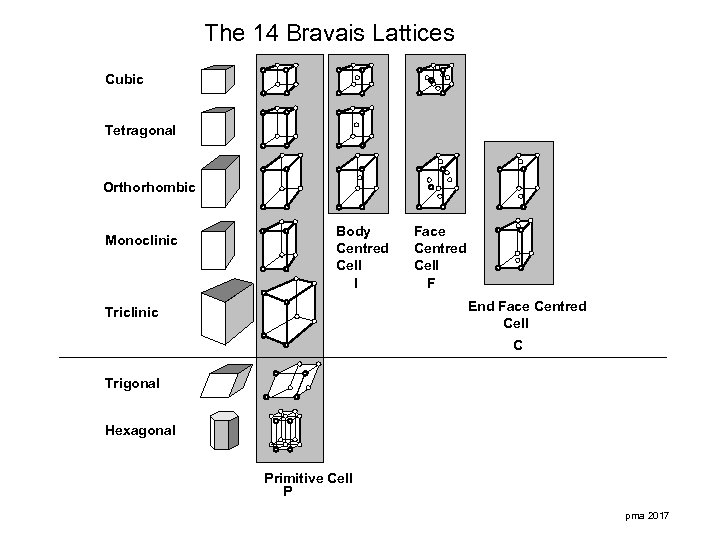
The 14 Bravais Lattices Cubic Tetragonal Orthorhombic Monoclinic Body Centred Cell I Face Centred Cell F End Face Centred Cell Triclinic C Trigonal Hexagonal Primitive Cell P pma 2017
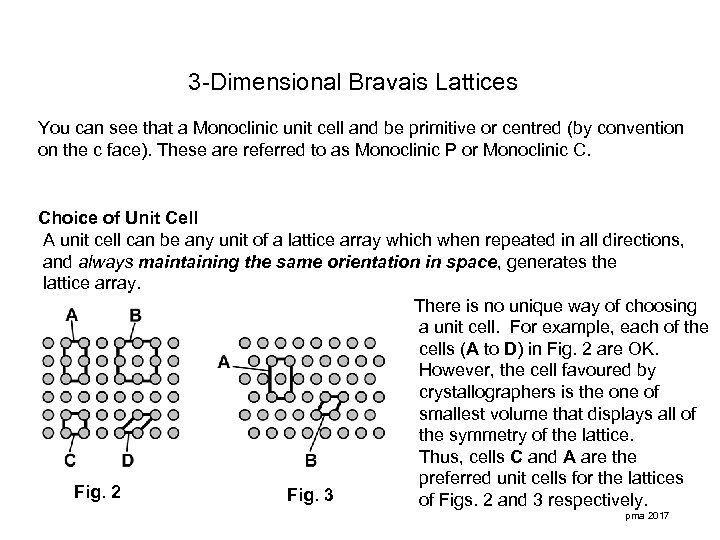
3 -Dimensional Bravais Lattices You can see that a Monoclinic unit cell and be primitive or centred (by convention on the c face). These are referred to as Monoclinic P or Monoclinic C. Choice of Unit Cell A unit cell can be any unit of a lattice array which when repeated in all directions, and always maintaining the same orientation in space, generates the lattice array. There is no unique way of choosing a unit cell. For example, each of the cells (A to D) in Fig. 2 are OK. However, the cell favoured by crystallographers is the one of smallest volume that displays all of the symmetry of the lattice. Thus, cells C and A are the preferred unit cells for the lattices Fig. 2 Fig. 3 of Figs. 2 and 3 respectively. pma 2017

Four important points on crystal lattices: 1. Every crystal system has a primitive Bravais lattice or P type. 2. The distribution of lattice points in a cell must be such as to maintain the total symmetry of the crystal system. Thus, the cubic system cannot have a C-type cell. 3. The fact that a unit cell meets the symmetry requirements of a crystal system does not guarantee its inclusion within the crystal system. This could result if the lattice it generated could be equally well represented by a unit cell type which is already included within the crystal system. The C-type cell for the tetragonal system (see Fig. 4) provides a good example. 4. If you apply point 3 to the orthorhombic system you will find that the primitive cell you generate will not have 90º angles. This would not be orthorhombic and thus orthorhombic C is included in the orthorhombic system. This is shown on the next slide. pma 2017
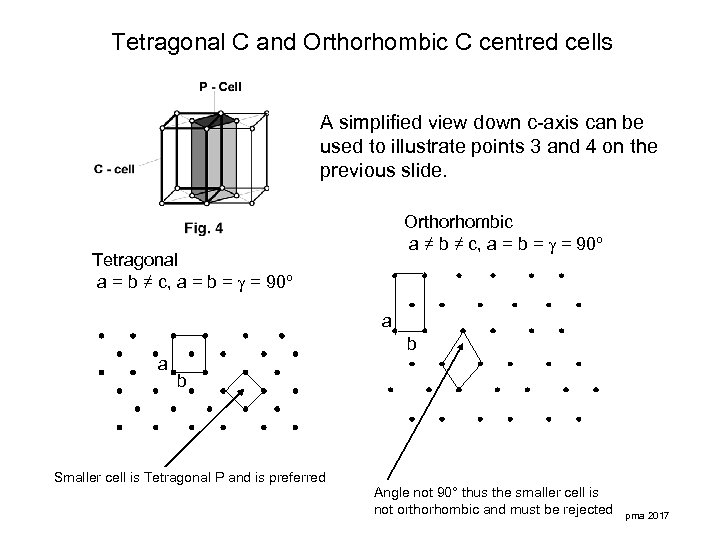
Tetragonal C and Orthorhombic C centred cells A simplified view down c-axis can be used to illustrate points 3 and 4 on the previous slide. Orthorhombic a ≠ b ≠ c, a = b = = 90º Tetragonal a = b ≠ c, a = b = = 90º a b Smaller cell is Tetragonal P and is preferred Angle not 90° thus the smaller cell is not orthorhombic and must be rejected pma 2017
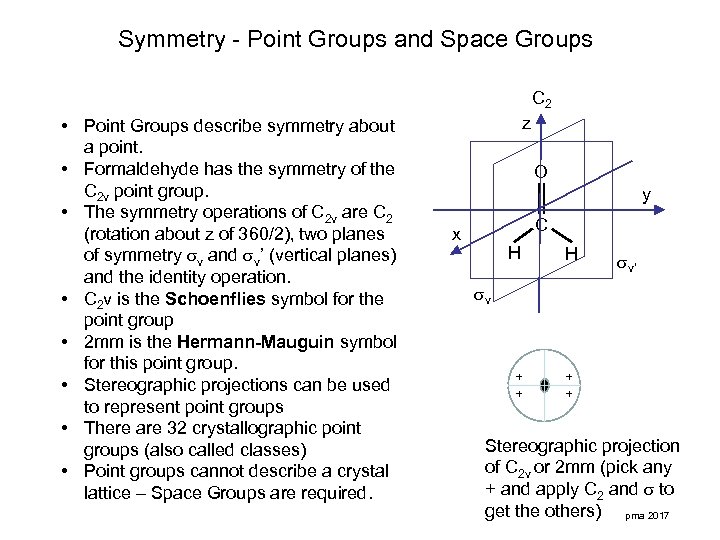
Symmetry - Point Groups and Space Groups C 2 • Point Groups describe symmetry about a point. • Formaldehyde has the symmetry of the C 2 v point group. • The symmetry operations of C 2 v are C 2 (rotation about z of 360/2), two planes of symmetry v and v’ (vertical planes) and the identity operation. • C 2 v is the Schoenflies symbol for the point group • 2 mm is the Hermann-Mauguin symbol for this point group. • Stereographic projections can be used to represent point groups • There are 32 crystallographic point groups (also called classes) • Point groups cannot describe a crystal lattice – Space Groups are required. z O y C x H H v’ v + + Stereographic projection of C 2 v or 2 mm (pick any + and apply C 2 and to get the others) pma 2017

Space Groups from Point Groups. Point Group symmetry operations (sym. ops. ) • Identity x, y, z → x, y, z • Inversion x, y, z → -x, -y, -z • Mirror e. g. xy plane mirror x, y, z → x, y, -z • Rotation axis rotation by 360/n n = 1, 2, 3, 4 or 6. Space Group sym. ops. also have translational symmetry – screw axes and glide planes A screw axis is represented by nm where n is the rotation (360/n) and m/n is the fraction of the unit cell length of the translation e. g. a 21 along b • 21 along b x, y, z → -x, 1/2+y, -z A glide plane has translation (often ½) and a reflection • b glide with a yz mirror x, y, z → -x, ½+y, z • Combining these symmetry operations with the 32 point groups leads to the 230 possible 3 d Space Groups. pma 2017

The 230 Space Groups The distribution of Space Groups among the Bravais lattice type is shown in Fig. 9. CRYSTAL SYSTEMS (7) BRAVAIS LATTICES (14) P F I SPACE GROUPS (230) 15 36 The International Tables for 11 10 Crystallography list the symmetry P 49 I 19 P F I C and A P 30 5 9 15 8 C 5 Triclinic P 2 2 Rhombohedral P and R 25 25 Hexagonal P 27 27 Cubic Tetragonal Orthorhombic Monoclinic Fig. 9 68 59 13 properties for all 230 Space Groups. The 2 nd edition was in one volume and edited by Kathleen Lonsdale. The current edition runs to 7 volumes. The CSD or Cambridge Data Base is a repository for the structures of organic and organometallic compounds. Space Group determination is an important step in crystal structure determination. pma 2017
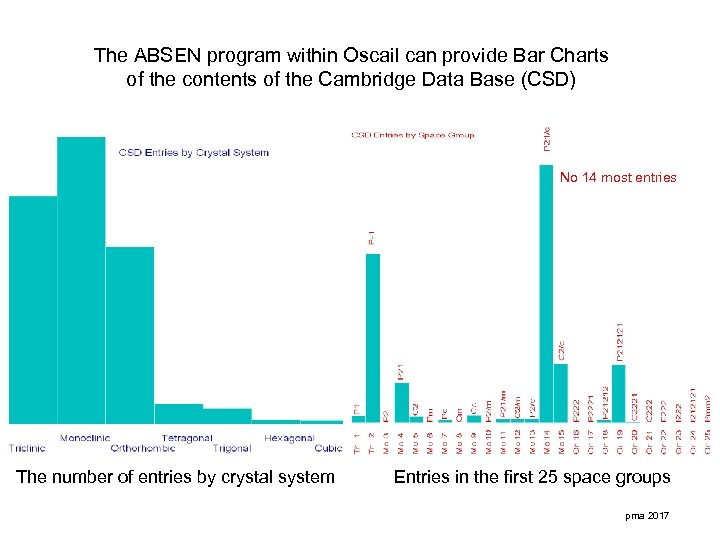
The ABSEN program within Oscail can provide Bar Charts of the contents of the Cambridge Data Base (CSD) No 14 most entries The number of entries by crystal system Entries in the first 25 space groups pma 2017

Space Group No. 14 P 21/c • • This monoclinic space group has the most entries on the CSD Read its name as “p 21 upon c” The full name is P 1 21/c 1 (there is no symmetry on a or c) There are 4 general positions 1 x, y, z 2 -x, 1/2+y, 1/2 -z 3 -x, -y, -z 4 x, 1/2 -y, 1/2+z 4 2 glide normal to screen at 1/4 b 1 3 Stereographic view down b 21 screw axis glide plane at 1/4 b View down a inversion centre pma 2017
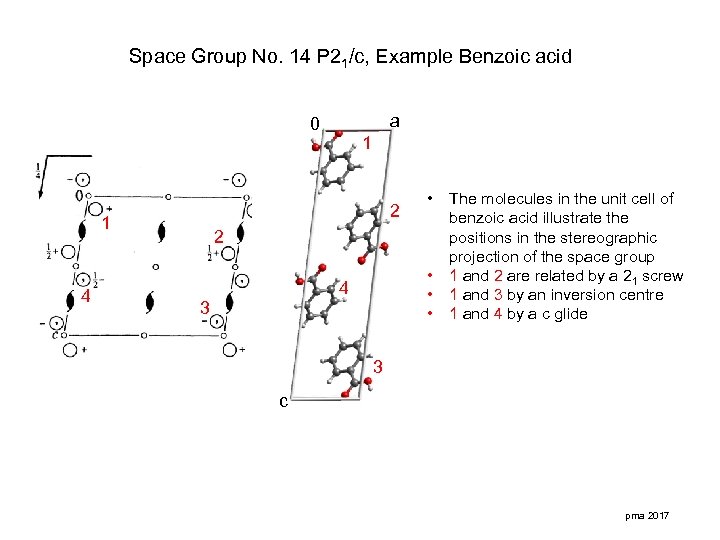
Space Group No. 14 P 21/c, Example Benzoic acid a 0 2 1 4 1 • 2 • • • 4 3 The molecules in the unit cell of benzoic acid illustrate the positions in the stereographic projection of the space group 1 and 2 are related by a 21 screw 1 and 3 by an inversion centre 1 and 4 by a c glide 3 c pma 2017
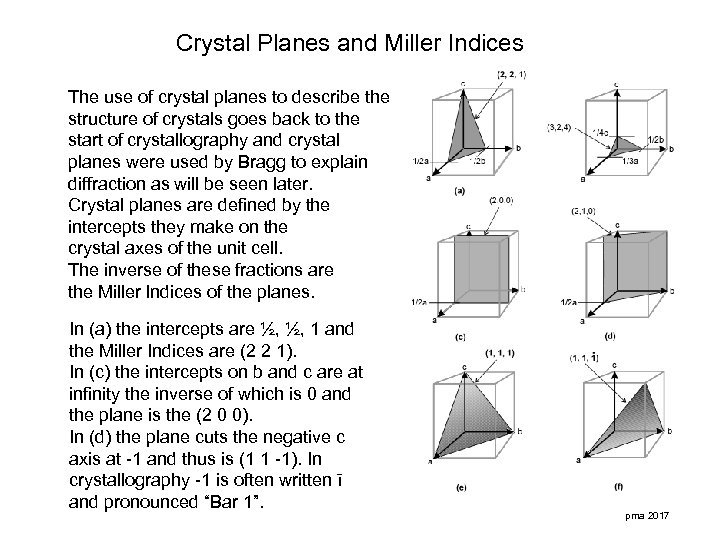
Crystal Planes and Miller Indices The use of crystal planes to describe the structure of crystals goes back to the start of crystallography and crystal planes were used by Bragg to explain diffraction as will be seen later. Crystal planes are defined by the intercepts they make on the crystal axes of the unit cell. The inverse of these fractions are the Miller Indices of the planes. In (a) the intercepts are ½, ½, 1 and the Miller Indices are (2 2 1). In (c) the intercepts on b and c are at infinity the inverse of which is 0 and the plane is the (2 0 0). In (d) the plane cuts the negative c axis at -1 and thus is (1 1 -1). In crystallography -1 is often written ī and pronounced “Bar 1”. pma 2017
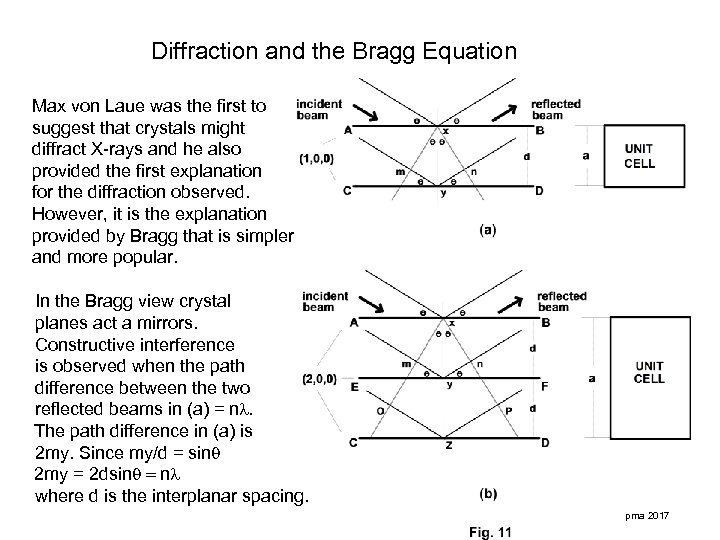
Diffraction and the Bragg Equation Max von Laue was the first to suggest that crystals might diffract X-rays and he also provided the first explanation for the diffraction observed. However, it is the explanation provided by Bragg that is simpler and more popular. In the Bragg view crystal planes act a mirrors. Constructive interference is observed when the path difference between the two reflected beams in (a) = n. The path difference in (a) is 2 my. Since my/d = sin 2 my = 2 dsin = n where d is the interplanar spacing. pma 2017

Bragg Reflection Order On the previous slide in (a) it is clear that the planes are the (1, 0, 0) set of planes. If the path difference is simply one wavelength the Bragg condition can be stated as This is a first order reflection. If the path difference is two wave lengths the Bragg condition becomes and the reflection is a second order reflection. pma 2017
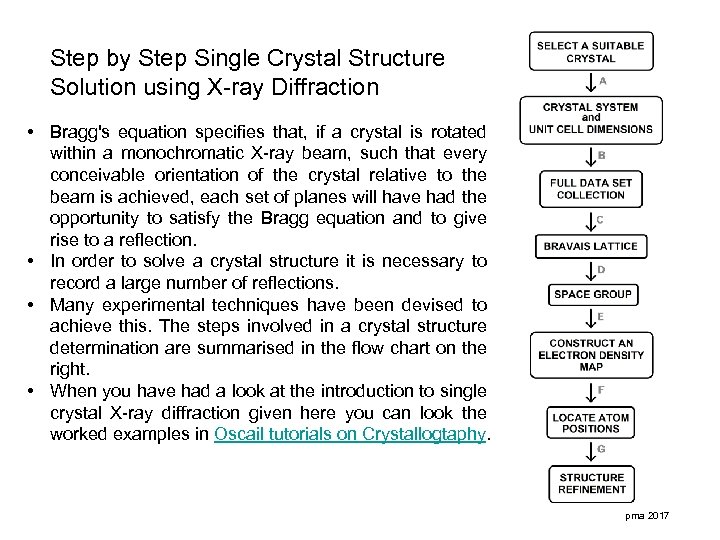
Step by Step Single Crystal Structure Solution using X-ray Diffraction • Bragg's equation specifies that, if a crystal is rotated within a monochromatic X-ray beam, such that every conceivable orientation of the crystal relative to the beam is achieved, each set of planes will have had the opportunity to satisfy the Bragg equation and to give rise to a reflection. • In order to solve a crystal structure it is necessary to record a large number of reflections. • Many experimental techniques have been devised to achieve this. The steps involved in a crystal structure determination are summarised in the flow chart on the right. • When you have had a look at the introduction to single crystal X-ray diffraction given here you can look the worked examples in Oscail tutorials on Crystallogtaphy. pma 2017

Single Crystal X-Ray Data Collection The first crystallographic data collection systems used photographic methods. Modern diffractometers use electronic area detectors which measure hundreds of reflections at a time. In a typical setup a crystal is oscillated over < 2° while an image is collected then the crystal is rotated by the same amount and oscillated again. The process is repeated over a total range of up to 180°. Data collection time depends on the crystal size, quality and other factors and may be from 40 mins to several hours. pma 2017

Determination of the Lattice type and Space Group High symmetry can lead to reflections being systematically absent from the data set. Absent reflections have no measurable intensity. There are two types of absences, General Absences and Special Absences. The general absences determine the lattice type; Primitive (P) has no general absences and no restrictions on h, k or l. End Cantered (C) h+k=2 n+1 are all absent. Face Cantered (F) only h, k, l, all even or all odd are observed. Body Cantered (I) h+k+l=2 n+1 are all absent. The special absences refer to specific sets of reflections and are used to detect the presence of glide planes and screw axes. Some Space Groups are uniquely determined by special absences but in many cases several Space Groups will have to be considered. Computer programs are able to lay out the data in tables with absences indicated and possible Space Groups can be suggested however the choice of Space Group will often need to be carefully considered. pma 2017
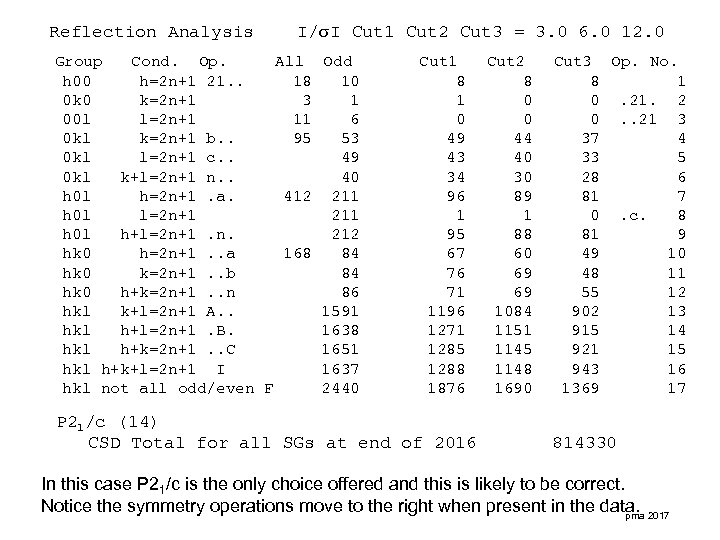
Reflection Analysis I/ I Cut 1 Cut 2 Cut 3 = 3. 0 6. 0 12. 0 Group Cond. Op. All h 00 h=2 n+1 21. . 18 0 k 0 k=2 n+1 3 00 l l=2 n+1 11 0 kl k=2 n+1 b. . 95 0 kl l=2 n+1 c. . 0 kl k+l=2 n+1 n. . h 0 l h=2 n+1. a. 412 h 0 l l=2 n+1 h 0 l h+l=2 n+1. n. hk 0 h=2 n+1. . a 168 hk 0 k=2 n+1. . b hk 0 h+k=2 n+1. . n hkl k+l=2 n+1 A. . hkl h+l=2 n+1. B. hkl h+k=2 n+1. . C hkl h+k+l=2 n+1 I hkl not all odd/even F Odd 10 1 6 53 49 40 211 212 84 84 86 1591 1638 1651 1637 2440 Cut 1 8 1 0 49 43 34 96 1 95 67 76 71 1196 1271 1285 1288 1876 P 21/c (14) CSD Total for all SGs at end of 2016 Cut 2 8 0 0 44 40 30 89 1 88 60 69 69 1084 1151 1145 1148 1690 Cut 3 Op. No. 8 1 0. 21. 2 0. . 21 3 37 4 33 5 28 6 81 7 0. c. 8 81 9 49 10 48 11 55 12 902 13 915 14 921 15 943 16 1369 17 814330 In this case P 21/c is the only choice offered and this is likely to be correct. Notice the symmetry operations move to the right when present in the data. 2017 pma
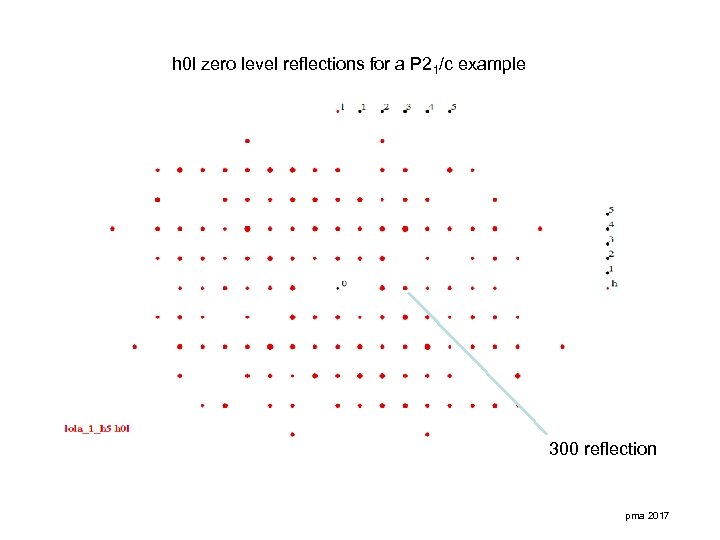
h 0 l zero level reflections for a P 21/c example 300 reflection pma 2017

Solving the Structure The unit cell, the Space Group and the reflection intensities cannot be used to generate the structure as there is no reflection phase information in the data set. This is the phase problem. If the reflection phases were known then an electron density map could be calculated using a Fourier series. If (x, y, z) is the electron density at x, y, z then The F here is the square root of the measured intensity When intensity is measured it is measured without sign and the phase is lost. There are three ways to solve the phase problem: 1. The Patterson or heavy atom method 2. Direct Methods (Hauptman and Karle 1985 Nobel prize) 3. The Charge flipping method is a recent development The Shelx. T program combines these methods automatically pma 2017

The Patterson or heavy atom method. It is the electrons that scatter X-rays. Atoms that are heavier than all others in the crystal will give rise to the strongest reflections. Heavy is a relative term however, all atoms after Rb are normally considered to be heavy. Iodine for example will scatter a lot of X-rays compared to carbon. Using the Patterson method it should be possible to calculate the position of an iodine atom and this could be used to phase most of the reflections and calculate an electron density map. Direct Methods After many years of study statistical trends were observed in reflection phases. It was also observed that some reflections are more important than others. The Direct Methods approach tries to guess the reflection phases and then awards a Figure of Merit to the guess. The most popular is the Combined Figure of Merit or CFOM). It is normal practice to accept solutions with CFOM values in the range 0. 03 -0. 15 and to try to use these phases to generate an electron density map. Charge Flipping The charge flipping method works well if the data has good resolution. There are examples in the Oscail crystallography tutorials. pma 2017

Refining a Structure It should be possible to “see” atoms in an electron density map if it has good resolution i. e. at least 1Å resolution. The steps in refining a structure are. 1. Use whatever atoms you have that look OK to generate an electron density map. 2. The known atoms are subtracted from this to generate a difference map. 3. Any atoms that have been missed should be in the difference map. 4. The refinement process minimises the difference between observed and calculated reflection intensities. 5. In the final difference map there should be no peaks larger than a H atom i. e. > 1 e/Å3. (A H atom has a volume of about 1Å3 and has 1 e. ) Resolution The resolution of a crystal structure is usually quoted in Angstroms, Å. Standard small molecule structures should always be at least of 1 Å resolution to give accurate bond lengths. Resolution can be related to Bragg angle at any wavelength through the Bragg equation n = 2 d sin. Using the value of the reflection with the largest Bragg angle in a data set then d = /2 sin gives the resolution. The pattern shown on slide 15 has a resolution of 0. 98Å at the edge. pma 2017

Final stages of refinement. There are many was in which a structure can be “improved”. The two most important considerations are addition of hydrogen atoms and anisotropic refinement of the non-hydrogen atoms. Addition of hydrogen atoms – Hydrogen atoms have only 1 electron and are often not seen in difference maps. It is best to include them at calculated positions. This is easy to do and it will improve the “R factor”. Anisotropic refinement of the non-hydrogen atoms – In the early stages atoms are refined as if they were spheres. Since atoms vibrate in a way that is controlled by chemical bonds and interactions with their neighbours, it is better to refine then as ellipsoids. One parameter (the radius) is enough to define a sphere this with x, y, z means that isotropic refinement requires 4 parameters per atom. An ellipsoid needs 6 parameters thus an anisotropic atom requires 9 parameters. This is an example of an anisotropic atom R Factor – The R factors used are Rw and w. R 2. Rw should be < 8% and w. R 2 should be <15%. The lower the better. If the R or error is greater then these values the structure is not much use. Rs are of the form Sum[(I 0 -Ic)/Io] pma 2017

Problems with single crystal X-ray Crystallography Locating Hydrogen atoms - Hydrogen atoms make extremely small contributions and for this reason X-ray crystallography is not a good technique for accurately locating hydrogen atom positions. If the location of hydrogen atoms is of specific interest (e. g. in the study of hydride structures and hydrogen bonding interactions) use has got to be made of the much more expensive and less available technique of neutron diffraction. The theory of neutron diffraction is very similar to that for X-ray diffraction but an essential difference is that hydrogen atoms scatter neutrons as effectively as many other atoms and for this reason they can be located with good accuracy in the structure determination. The Need for Single Crystals - In order to carry out a detailed X-ray structure determination, it is essential to have a crystal of the material in question. Many compounds cannot be crystallised and thus are not amenable to diffraction studies. There also commercially important materials such as glasses and many ceramics which owe their unique properties to their amorphous nature. Being amorphous (no long range order), the structures of these materials cannot be investigated in detail by diffraction techniques. Low Temperature Structure Determination – When X-ray data are collected at low temperature (<-150 ºC) thermal ellipsoids are smaller and better defined. N. B. bond lengths show very little variation with temperature. pma 2017
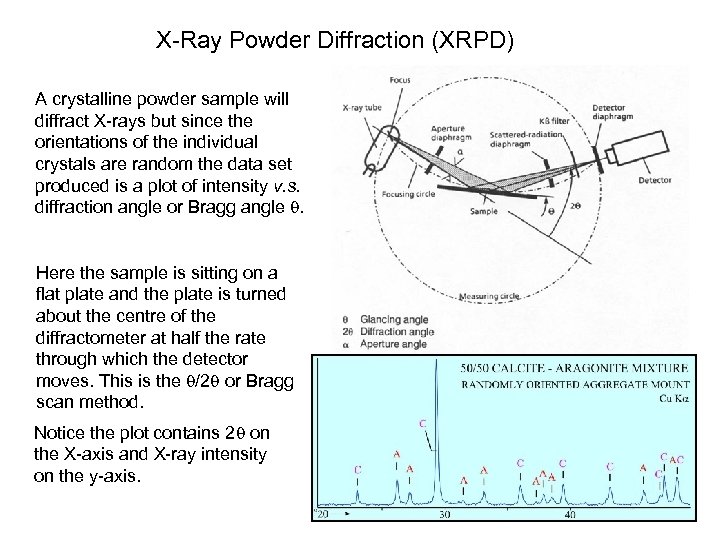
X-Ray Powder Diffraction (XRPD) A crystalline powder sample will diffract X-rays but since the orientations of the individual crystals are random the data set produced is a plot of intensity v. s. diffraction angle or Bragg angle . Here the sample is sitting on a flat plate and the plate is turned about the centre of the diffractometer at half the rate through which the detector moves. This is the /2 or Bragg scan method. Notice the plot contains 2 on the X-axis and X-ray intensity on the y-axis. pma 2017

Uses of X-ray Powder Diffraction In general, powder diffraction data are unsuitable for solving crystal structures. Some advances have recently been made using the Rietveld method. However this is far from trivial and it works best in relatively simple cases. It is very difficult to be sure that the unit cell is correct as the reflections overlap and are difficult to resolve from one another. There may also be problems with preferred orientation of crystallites. Important advantages and uses of powder diffraction: 1. The need to grow crystals is eliminated. 2. A powder diffraction pattern can be recorded very rapidly and the technique is non-destructive. 3. With special equipment very small samples may be used (1 -2 mg. ) 4. A powder diffraction pattern may be used as a fingerprint. It is often superior to an infrared spectrum in this respect. 5. It can be used for the qualitative, and often the quantitative, determination of the crystalline components of a powder mixture. 6. Powder diffractometry provides an easy and fast method for the detection of crystal polymorphs. Powder patterns are provided when a drug is being registered with the FDA. (Polymorphs are different crystal forms of the same substance. ) pma 2017
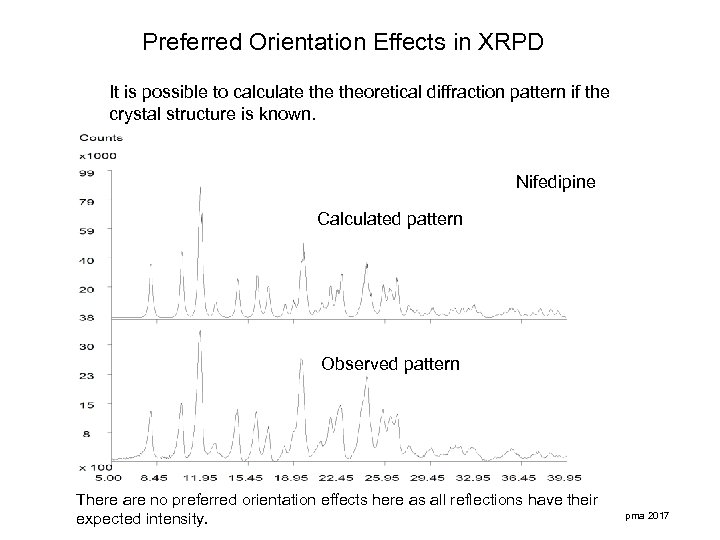
Preferred Orientation Effects in XRPD It is possible to calculate theoretical diffraction pattern if the crystal structure is known. Nifedipine Calculated pattern Observed pattern There are no preferred orientation effects here as all reflections have their expected intensity. pma 2017
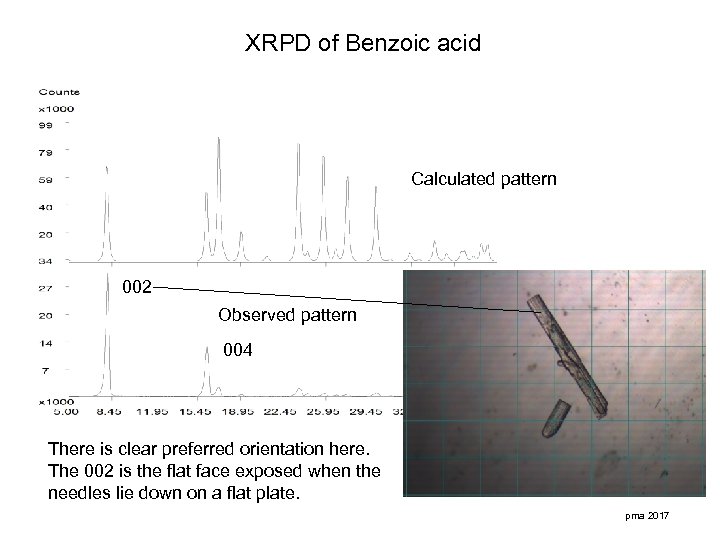
XRPD of Benzoic acid Calculated pattern 002 Observed pattern 004 There is clear preferred orientation here. The 002 is the flat face exposed when the needles lie down on a flat plate. pma 2017

Some points relating to preferred orientation effects. • Preferred orientation effects are often observed for needles and plates. • Preferred orientation effects can be reduced by sample rotation and sample grinding. • When an indexed calculated pattern is compared to that of a sample showing preferred orientation it may be possible to to index the faces of plate like crystals. • Deviations from calculated patterns can be used to monitor the crystal morphology of production batches. pma 2017
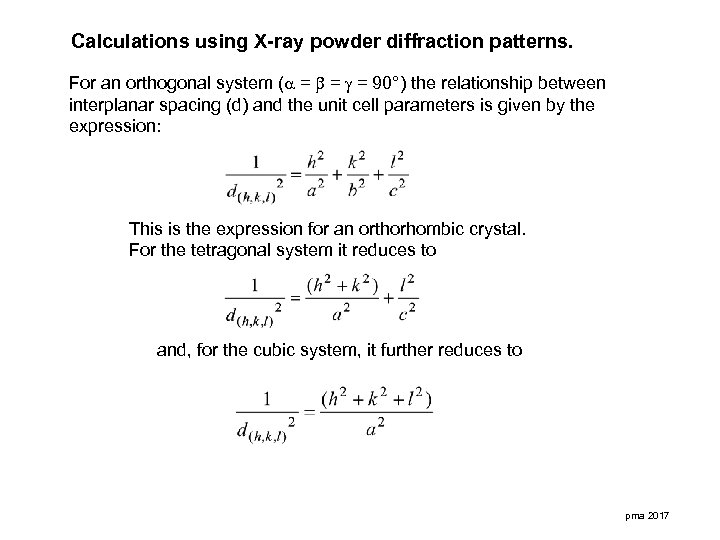
Calculations using X-ray powder diffraction patterns. For an orthogonal system ( = = = 90°) the relationship between interplanar spacing (d) and the unit cell parameters is given by the expression: This is the expression for an orthorhombic crystal. For the tetragonal system it reduces to and, for the cubic system, it further reduces to pma 2017
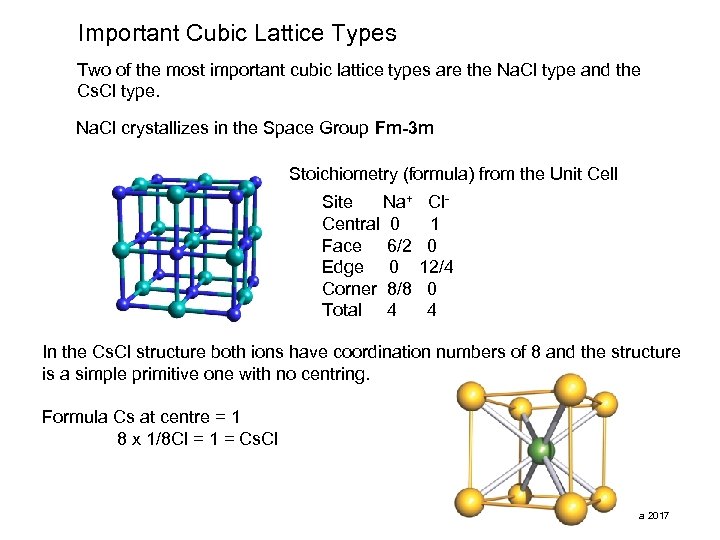
Important Cubic Lattice Types Two of the most important cubic lattice types are the Na. Cl type and the Cs. Cl type. Na. Cl crystallizes in the Space Group Fm-3 m Stoichiometry (formula) from the Unit Cell Site Na+ Central 0 Face 6/2 Edge 0 Corner 8/8 Total 4 Cl 1 0 12/4 0 4 In the Cs. Cl structure both ions have coordination numbers of 8 and the structure is a simple primitive one with no centring. Formula Cs at centre = 1 8 x 1/8 Cl = 1 = Cs. Cl pma 2017
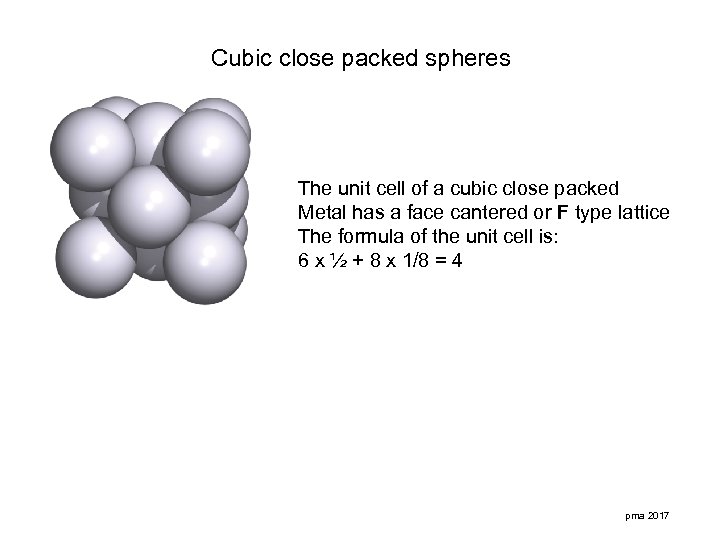
Cubic close packed spheres The unit cell of a cubic close packed Metal has a face cantered or F type lattice The formula of the unit cell is: 6 x ½ + 8 x 1/8 = 4 pma 2017

The Bragg equation may be rearranged (if n=1) from to If the value of 1/(dh, k, l)2 in the cubic system equation above is inserted into this form of the Bragg equation you have Since in any specific case a and are constant and if 2/4 a 2 = A pma 2017

Analysis Cubic XRPD patterns Example 1 Aluminium powder gives a diffraction pattern that yields the following eight largest d-spacings: 2. 338, 2. 024, 1. 431, 1. 221, 1. 169, 1. 0124, 0. 9289 and 0. 9055 Å. Aluminium has a cubic close packed structure and its atomic weight is 26. 98 and = 1. 5405 A. Problem - Index the diffraction data and calculate the density of aluminium. The Bragg equation, can be used to obtain sin , The ccp lattice is an F type lattice and the only reflections observed are those with all even or all odd indices. Thus the only values of sin 2 in that are allowed are 3 A, 4 A , 8 A, 11 A, 12 A, 16 A and 19 A for the first eight reflections. pma 2017
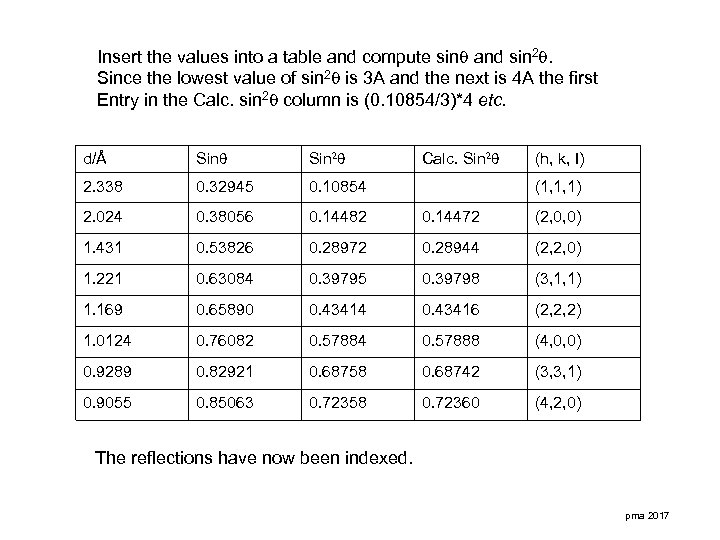
Insert the values into a table and compute sin and sin 2. Since the lowest value of sin 2 is 3 A and the next is 4 A the first Entry in the Calc. sin 2 column is (0. 10854/3)*4 etc. d/Å Sin 2 Calc. Sin 2 2. 338 0. 32945 0. 10854 2. 024 0. 38056 0. 14482 0. 14472 (2, 0, 0) 1. 431 0. 53826 0. 28972 0. 28944 (2, 2, 0) 1. 221 0. 63084 0. 39795 0. 39798 (3, 1, 1) 1. 169 0. 65890 0. 43414 0. 43416 (2, 2, 2) 1. 0124 0. 76082 0. 57884 0. 57888 (4, 0, 0) 0. 9289 0. 82921 0. 68758 0. 68742 (3, 3, 1) 0. 9055 0. 85063 0. 72358 0. 72360 (4, 2, 0) (h, k, I) (1, 1, 1) The reflections have now been indexed. pma 2017

Calculation of a For the first reflection (for which h 2 + k 2 + l 2 = 3) sin 2 = 3 A = 3 ( 2 / 4 a 2 ) a 2 = 3 2 / 4 sin 2 a = 4. 04946 Å = 4. 04946 x 10 -8 cm. Calculation of the density of aluminium a 3 = 66. 40356 Å3 = 66. 40356 x 10 -24 cm 3. If the density of aluminium is (g. cm. -3), the mass of the unit cell is x 66. 40356 x 10 -24 g. The unit cell of aluminium contains 4 atoms. The weight of one aluminium atom is 26. 98/(6. 022 x 1023) = 4. 48024 x 10 -23 and the weight of four atoms (the content of the unit cell) is 179. 209 x 10 -24. x 66. 40356 x 10 -24 = 179. 209 x 10 -24 p = 2. 6988 g. cm-3. pma 2017
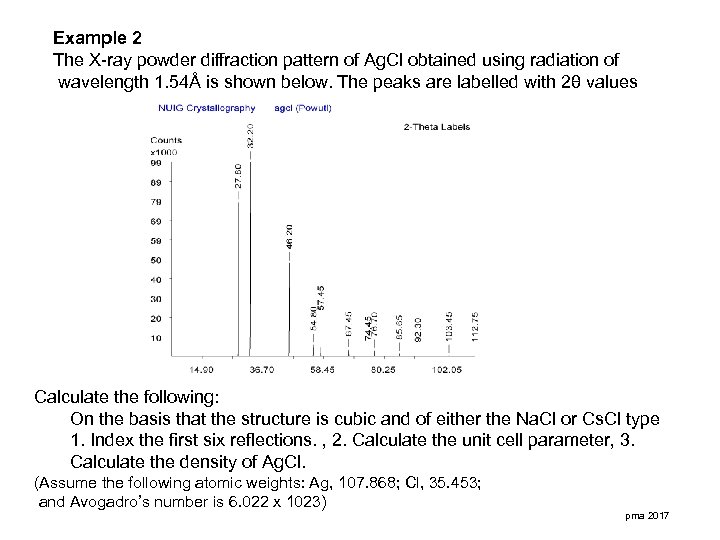
Example 2 The X-ray powder diffraction pattern of Ag. Cl obtained using radiation of wavelength 1. 54Å is shown below. The peaks are labelled with 2θ values Calculate the following: On the basis that the structure is cubic and of either the Na. Cl or Cs. Cl type 1. Index the first six reflections. , 2. Calculate the unit cell parameter, 3. Calculate the density of Ag. Cl. (Assume the following atomic weights: Ag, 107. 868; Cl, 35. 453; and Avogadro’s number is 6. 022 x 1023) pma 2017
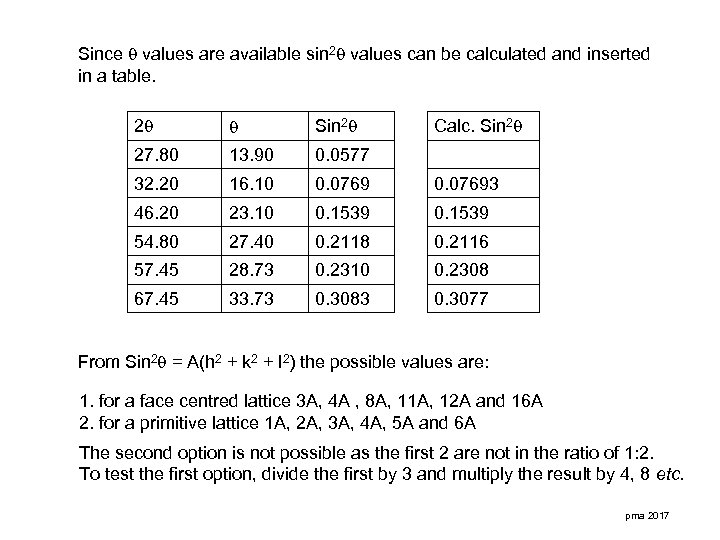
Since values are available sin 2 values can be calculated and inserted in a table. 2 Sin 2 Calc. Sin 2 27. 80 13. 90 0. 0577 32. 20 16. 10 0. 07693 46. 20 23. 10 0. 1539 54. 80 27. 40 0. 2118 0. 2116 57. 45 28. 73 0. 2310 0. 2308 67. 45 33. 73 0. 3083 0. 3077 From Sin 2 = A(h 2 + k 2 + l 2) the possible values are: 1. for a face centred lattice 3 A, 4 A , 8 A, 11 A, 12 A and 16 A 2. for a primitive lattice 1 A, 2 A, 3 A, 4 A, 5 A and 6 A The second option is not possible as the first 2 are not in the ratio of 1: 2. To test the first option, divide the first by 3 and multiply the result by 4, 8 etc. pma 2017

Density of Ag. Cl Since sin 2 = 2(h 2 + k 2 + l 2)/4 a 2 = (1. 54)2. (16)/4(0. 3083) using the largest (most accurate) 2 a 2 = 30. 7692 a = 5. 547Ǻ (1Ǻ = 10 -8 cm) Formula wt. of unit cell = 4 Ag. Cl = 573. 284 g This is the weight of 4 moles of Ag. Cl. The weight of 4 molecules is 573. 284 / (6. 02 x 1023) Density = 573. 284 / (6. 02 x 1023)(5. 547 x 10 -8)3 A is in Ǻ thus the answer should be multiplied by 1 / 10 -24 Density = 5. 580 g/cm 3 pma 2017
6136b0fe5b537ebc03c91cb239d41601.ppt