An Automated System for Floating- to Fixed-Point Conversion

“An Automated System for Floating- to Fixed-Point Conversion of High Performance of MATLAB Algorithms in FPGAs and ASICs” Eric Cigan and Robert Anderson September 2004

Outline § Motivation § For FPGA / ASIC implementation § For fixed-point arithmetic § Alternatives § Related approaches methods used § Changshun Shi – performance criteria and optimization § Approach used § MATLAB-based algorithmic synthesis § Heuristic-based approach § Advantages of approach § Single design source § Verification flow § Example § FIR filter EW Cigan 2 MAPLD 2004

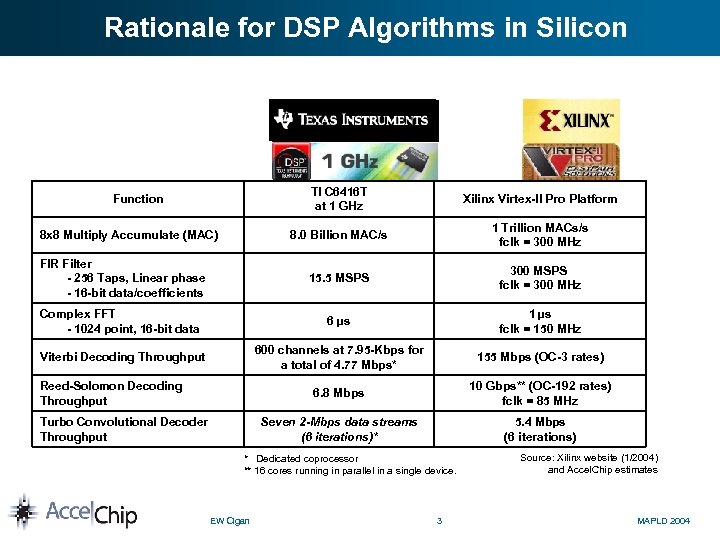Rationale for DSP Algorithms in Silicon TI C 6416 T at 1 GHz Xilinx Virtex-II Pro Platform 8 x 8 Multiply Accumulate (MAC) 8. 0 Billion MAC/s 1 Trillion MACs/s fclk = 300 MHz FIR Filter - 256 Taps, Linear phase - 16 -bit data/coefficients 15. 5 MSPS 300 MSPS fclk = 300 MHz Complex FFT - 1024 point, 16 -bit data 6 µs 1 µs fclk = 150 MHz Viterbi Decoding Throughput 600 channels at 7. 95 -Kbps for a total of 4. 77 Mbps* 155 Mbps (OC-3 rates) 6. 8 Mbps 10 Gbps** (OC-192 rates) fclk = 85 MHz Seven 2 -Mbps data streams (6 iterations)* 5. 4 Mbps (6 iterations) Function Reed-Solomon Decoding Throughput Turbo Convolutional Decoder Throughput * Dedicated coprocessor ** 16 cores running in parallel in a single device. EW Cigan 3 Source: Xilinx website (1/2004) and Accel. Chip estimates MAPLD 2004

Fixed-Point Implications § Increases in performance (throughput, frequency, etc. ) § In communications a 1 d. B increase in the link power budget results in a 25% increase in coverage § Power consumption § Word size = silicon area/memory => Cost Source: The Math. Works, 2003 EW Cigan 4 MAPLD 2004

Previous Work § Rule-of-thumb methods § § § Ad-hoc methods such as rounding and truncation. Manual scaling to and from integer representations. Recoding the source code in a hardware description language and then verifying performance in the RTL code. Substitution of floating-point functions with fixed-point equivalents, such as in C fixed-point libraries. Recent research § Keding, et al (RWTH Aachen, 1998) § § Algorithm described in C/C++ Oriented toward minimizing all wordlengths at same time Can require large number of iterations Shi and Brodersen (UC Berkeley, 2002 -2004) § § § Algorithm described in graphical design tool Optimization-based methodology Requires Monte Carlo simulation runs EW Cigan 5 MAPLD 2004

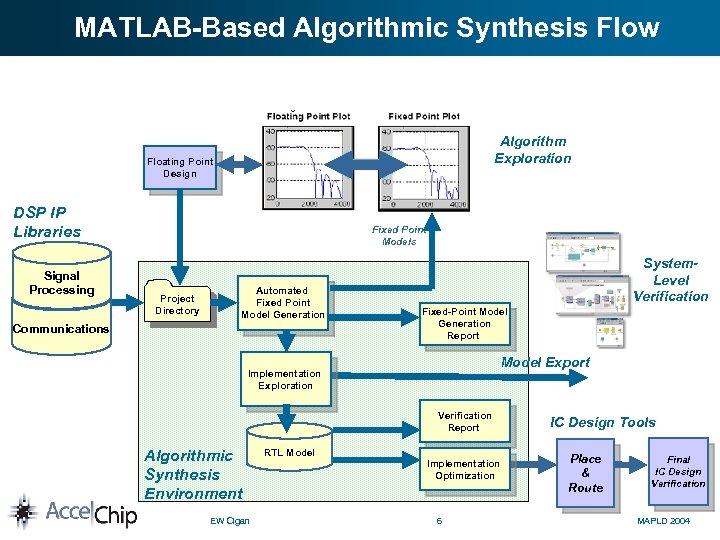MATLAB-Based Algorithmic Synthesis Flow Algorithm Exploration Floating Point Design DSP IP Libraries Signal Processing Fixed Point Models Project Directory Automated Fixed Point Model Generation Communications System. Level Verification Fixed-Point Model Generation Report Model Export Implementation Exploration Verification Report Algorithmic Synthesis Environment EW Cigan RTL Model Implementation Optimization 6 IC Design Tools Place & Route Final IC Design Verification MAPLD 2004

Synthesizable MATLAB Coding Basics § MATLAB script file applies input vectors to the design function in a loop called the “streaming loop” § The design to be synthesized needs to exist in a function called the design function § Additional MATLAB files or external data files may exist EW Cigan 7 MAPLD 2004

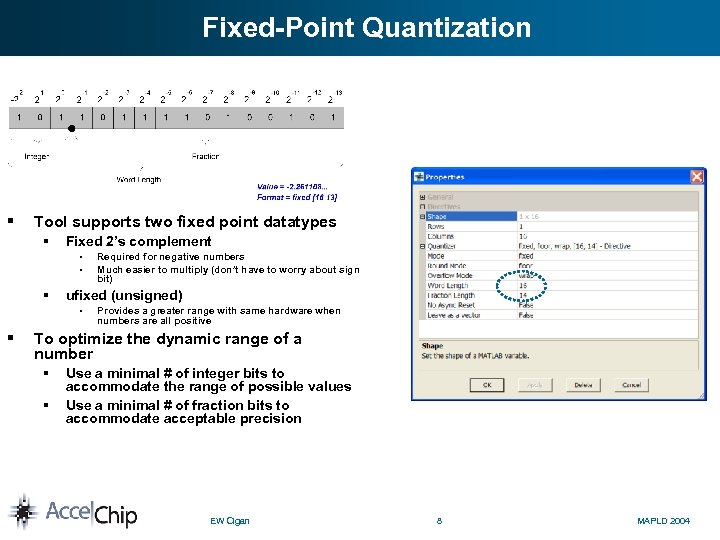Fixed-Point Quantization § Tool supports two fixed point datatypes § Fixed 2’s complement § § § ufixed (unsigned) § § Required for negative numbers Much easier to multiply (don’t have to worry about sign bit) Provides a greater range with same hardware when numbers are all positive To optimize the dynamic range of a number § § Use a minimal # of integer bits to accommodate the range of possible values Use a minimal # of fraction bits to accommodate acceptable precision EW Cigan 8 MAPLD 2004

Automated Quantization Method § Quantization performed on floating-point MATLAB § Bit widths are derived from § Stimulus waveforms § Text files loaded to initialize constants § Bit growth propagated from arithmetic operations § MATLAB quantizer statements in M-file § Explicit quantizer directives EW Cigan 9 MAPLD 2004

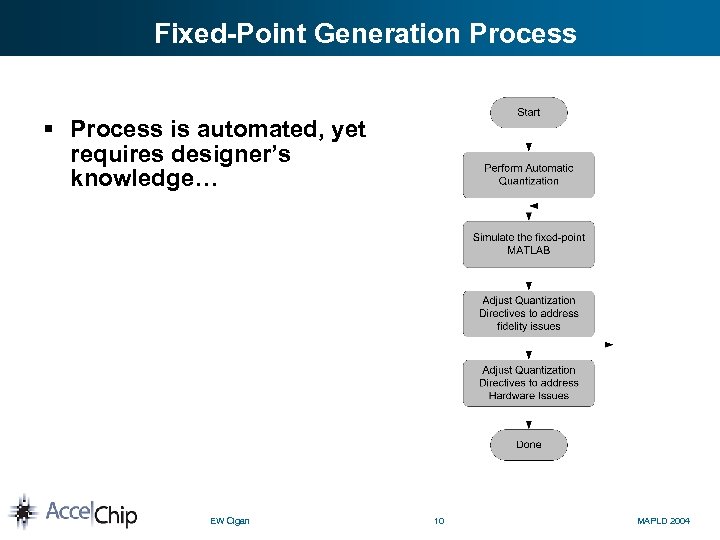Fixed-Point Generation Process § Process is automated, yet requires designer’s knowledge… EW Cigan 10 MAPLD 2004

Generated Fixed-Point MATLAB Files § Tool generates fixed-point M-files from source floating point Mfiles § The MATLAB “quantize” and “quantizer” functions are inserted into the original source code § Optimization of quantizer functions reduces simulation overhead of fixed-point simulation – up to 100 x faster Floating Point MATLAB Generated Fixed-Point Output EW Cigan 11 MAPLD 2004

The Quantize Directive § § § The Quantize directive allows users to override the automatic quantization Applying directive allows use of unmodified MATLAB source Directives can be typed at the command line or added to an “. add” directives file § Accel. Chip will create this file automatically when “Save -> Project” is executed Directives file located here Quantize directives can be applied interactively from the design browser Set. Directive Variables. indatabuf -quantize {fixed floor wrap {32 16}} EW Cigan 12 MAPLD 2004

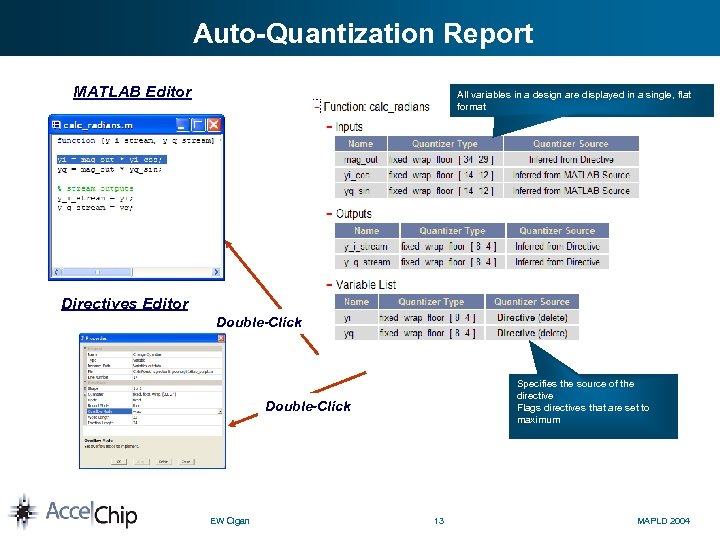Auto-Quantization Report MATLAB Editor All variables in a design are displayed in a single, flat format Directives Editor Double-Click Specifies the source of the directive Flags directives that are set to maximum Double-Click EW Cigan 13 MAPLD 2004

Overflow and Underflow § An underflow is defined as a number that is nonzero before it is quantized, and zero after it is quantized. § Example of an underflow: X = quantize(quantizer(‘ufixed’, ’floor’, ’wrap’, [2 2]), 0. 1); 00 b 01 b 10 b 11 b = = 0 0. 25 0. 50 0. 75 X will be zero because the smallest non-zero number will be too large § An overflow occurs when the magnitude of a number exceeds the dynamic range allowable by the integer bits as defined by the quantizer § Example of an overflow: X = quantize(quantizer(‘ufixed’, ’floor’, ’wrap’, [2 0]), 5); 00 b 01 b 10 b 11 b § = = 0 1 2 3 X will be one because the binary representation of 5, “ 101” will be wrapped to “ 01” A fidelity error is caused by either an overflow or an underflow § § Overflow errors tend to be severe distortions Underflow errors tend to be minor distortions EW Cigan 14 MAPLD 2004

Managing Underflow and Overflow Issues § Often a design has a large number of underflows and only a few overflows. § Displaying overflow and underflow messages together often makes it difficult to locate the overflows § Recommended Practice: § Begin the debug process by setting “Show Underflows” to False § Once overflows are addressed then set “Show Underflows” to True and Project options are available to address any remaining selectively disable displaying overflow or underflow message fidelity issues EW Cigan 15 MAPLD 2004

Addressing Bit Growth Due to Constants A constant introduced here Will affect all downstream hardware § Constants are represented in binary form with maximum accuracy § This can lead to unnecessary bit growth § Constants used directly in expressions can’t be quantized directly § Change in coding style allows bit growth management Y = x + quantize( quantizer(‘ufixed', 'floor', 'wrap ', [ 10, 9]), 1. 3 ) Y = x + 1. 3 or Const = 1. 3 Y = x + cost EW Cigan Recommended 16 MAPLD 2004

Improving Hardware through Quantization § Quantization can have a dramatic affect on performance and area § Tool will attempt to auto-quantize to preserve signal fidelity § A maximum of 53 bits will be used for internal variables § Consistent with abscissa of MATLAB “double” number § A maximum of 32 bits will be used for IO ports § Start by reviewing the fractional bits of the default quantization assigned to constants and the input data stream § Tool will use as much precision as necessary to represent number § E. g. , 0. 375 = 011 and 0. 3 = 01100110011001100110011001100 § Designer uses tool directives to trim bits Example – 16 -tap FIR filter Quantization on Filter Coefficients # of Slices Fixed, wrap, floor, [10 8] 55 Fixed, wrap, floor, [53 51]* 169 * Default quantization used 53 bits EW Cigan 17 MAPLD 2004

Conclusion § Algorithmic synthesis tool enables MATLAB design to be design source throughout process § Tool aids in automating process of converting floating point designs to fixed-point § Provides design exploration to increase performance and reduce size/power MATLAB Domain (Pure algorithmic non-implementation-specific) Untimed C Domain (non-implementation-specific) “m” language (used by MATLAB) More abstract, less implementationspecific Standard C (used by Catapult C) Timed C Domain Handel-C (implementation-specific) System. C RTL Domain Verilog and/or VHDL Less abstract, more implementationspecific (implementation-specific) Different levels of synthesis abstraction [source: Mentor Graphics white paper, “Catapult C Synthesis-based Design Flow, ” October 2003] EW Cigan 18 MAPLD 2004