f3fc52baff698605542a76e8268b8c36.ppt
- Количество слайдов: 99

An Adaptive Data Analysis Method with Some Biomedical Applications Norden E. Huang Research Center for Adaptive Data Analysis National Central University 2008

Data and Data Analysis Data are the our only connection to the reality. We are overwhelmed by the quantity of the data, But underserved by the quality of the analysis.

Data Processing and Data Analysis • Processing [proces < L. Processus < pp of Procedere = Proceed: pro- forward + cedere, to go] : A particular method of doing something. • Data Processing >>>> Mathematically meaningful parameters • Analysis [Gr. ana, up, throughout + lysis, a loosing] : A separating of any whole into its parts, especially with an examination of the parts to find out their nature, proportion, function, interrelationship etc. • Data Analysis >>>> Physical understandings

Henri Poincaré Science is built up of facts*, as a house is built of stones; but an accumulation of facts is no more a science than a heap of stones is a house. * Unexamined facts (data) are useless!

Scientific Activities Collecting, analyzing, synthesizing, and theorizing are the core of scientific activities. Data are our only connection to reality; they are also what separate science from philosophy. Therefore, data analysis is a key link in this continuous loop.

Data Analysis Data analysis is too important to be left to the mathematicians. Why? !

Different Paradigms I Mathematics vs. Science/Engineering • Mathematicians • Scientists/Engineers • Absolute proofs • Agreement with observations • Logic consistency • Physical meaning • Mathematical rigor • Working Approximations

Different Paradigms II Mathematics vs. Science/Engineering • Mathematicians • Scientists/Engineers • Idealized Spaces • Real Space • Perfect world in which everything is known • Real world in which knowledge is incomplete and limited • Inconsistency in the different spaces and the real world • Constancy in the real world within allowable approximation

Rigor vs. Reality As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality. Albert Einstein

Traditional Data Analysis In pursue of mathematic rigor and certainty, however, we are forced to idealize, but also deviate from, the reality. As a result, we are forced to live in a pseudo-real world, in which all processes are Linear and Stationary

削足適履 Trimming the foot to fit the shoe.

Available ‘Data Analysis’ Methods for Nonstationary (but Linear) time series • • Spectrogram Wavelet Analysis Wigner-Ville Distributions Empirical Orthogonal Functions aka Singular Spectral Analysis • Moving means • Successive differentiations

Available ‘Data Analysis’ Methods for Nonlinear (but Stationary and Deterministic) time series • Phase space method • Delay reconstruction and embedding • Poincaré surface of section • Self-similarity, attractor geometry & fractals • Nonlinear Prediction • Lyapunov Exponents for stability

Typical Apologia • Assuming the process is stationary …. • Assuming the process is locally stationary …. • As the nonlinearity is weak, we can use perturbation approach …. Though we can assume all we want, but the reality cannot be bent by the assumptions.

掩耳盜鈴 Stealing the bell with muffed ears

Motivations for alternatives: Problems for Traditional Methods • Physical processes are mostly nonstationary • Physical Processes are mostly nonlinear • Data from observations are invariably too short • Physical processes are mostly non-repeatable. Ensemble mean impossible, and temporal mean might not be meaningful for lack of stationarity and ergodicity. Traditional methods are inadequate.

The Job of a Scientist The job of a scientist is to listen carefully to nature, not to tell nature how to behave. Richard Feynman To listen is to use adaptive method and let the data sing, and not to force the data to fit preconceived modes.

Characteristics of Data from Nonlinear Processes

Duffing Pendulum x
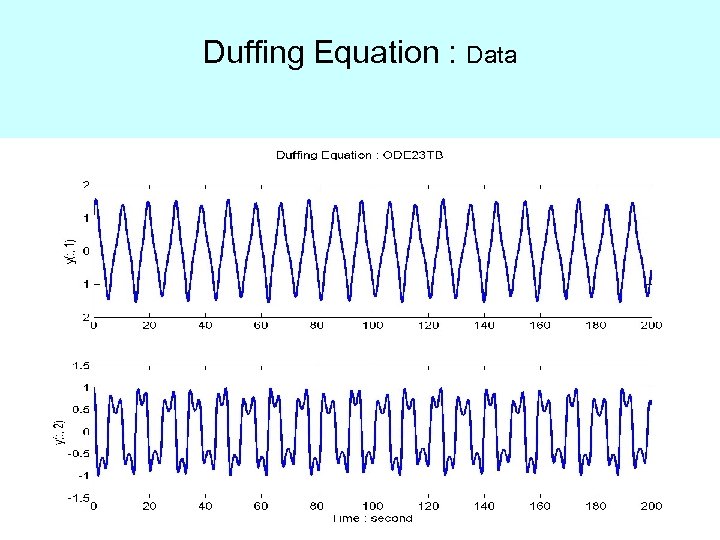
Duffing Equation : Data

Hilbert Transform : Definition
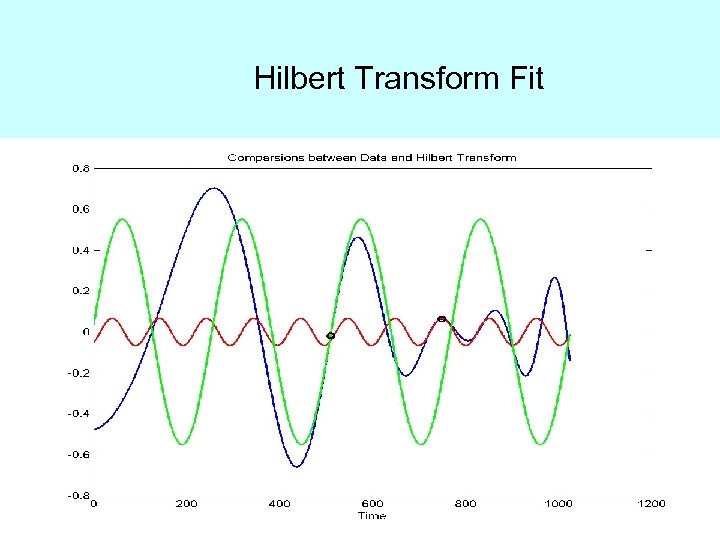
Hilbert Transform Fit

The Traditional View of the Hilbert Transform for Data Analysis
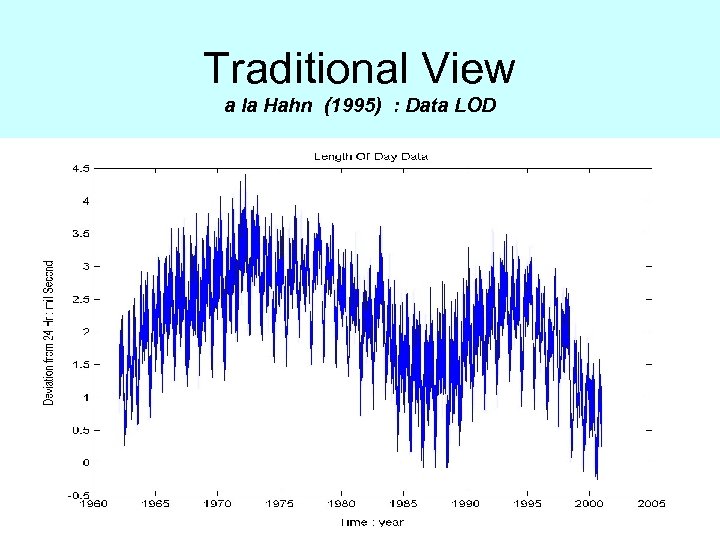
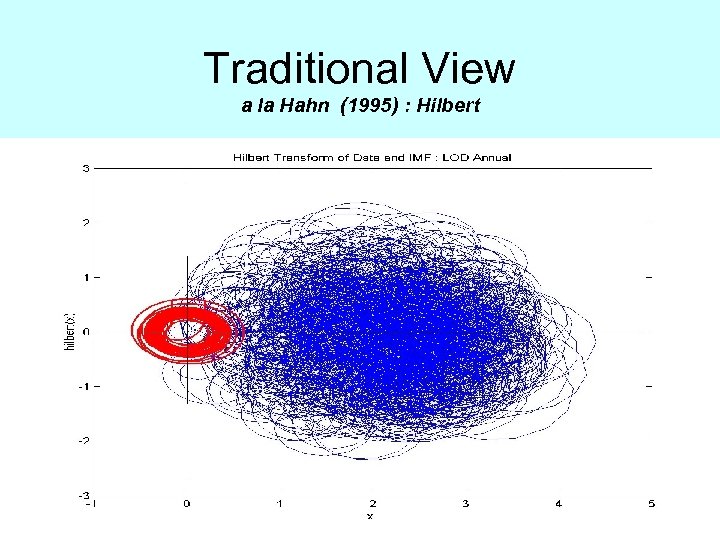
Traditional View a la Hahn (1995) : Data LOD
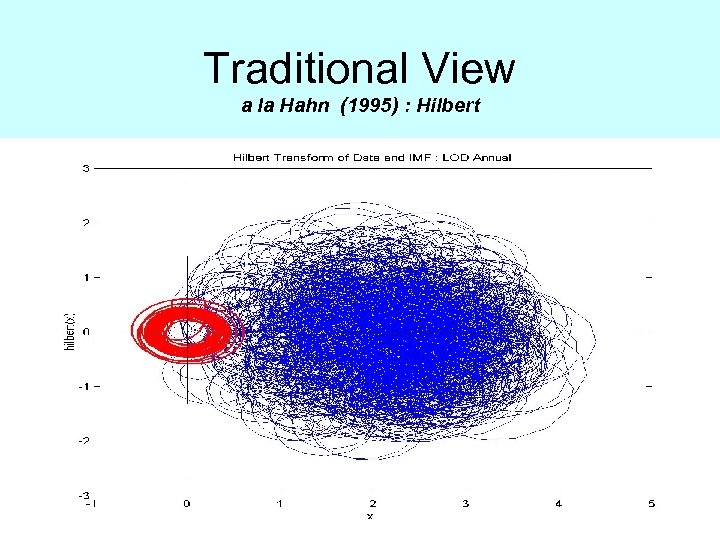
Traditional View a la Hahn (1995) : Hilbert

Why the traditional approach does not work?
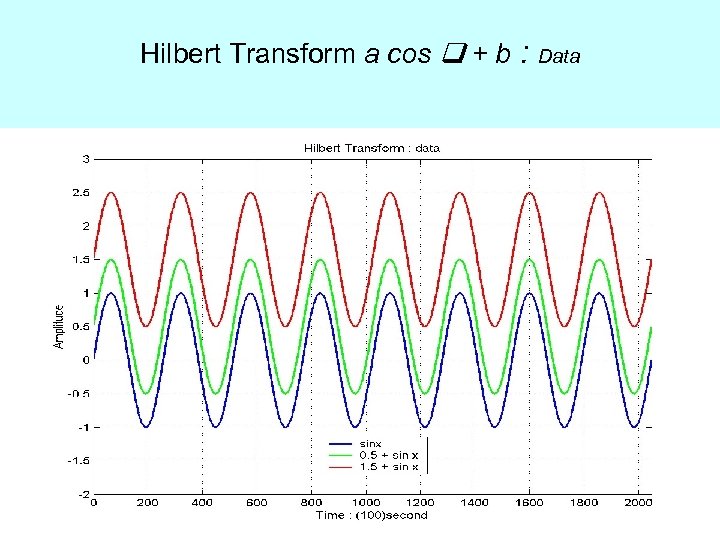
Hilbert Transform a cos + b : Data
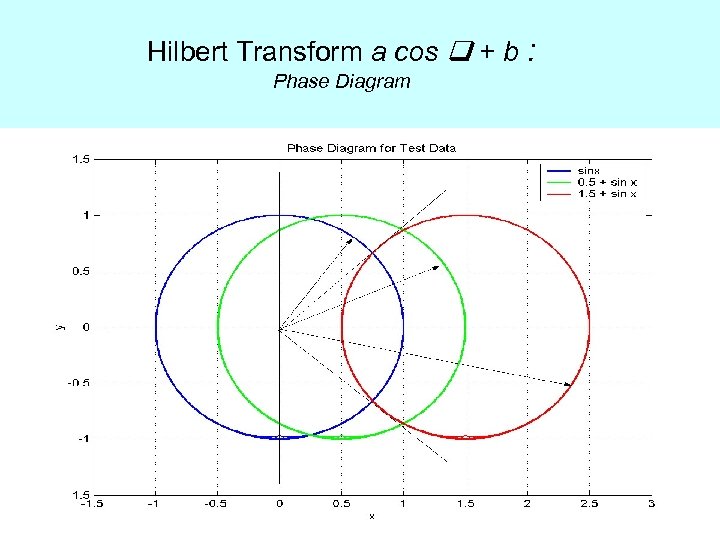
Hilbert Transform a cos + b : Phase Diagram
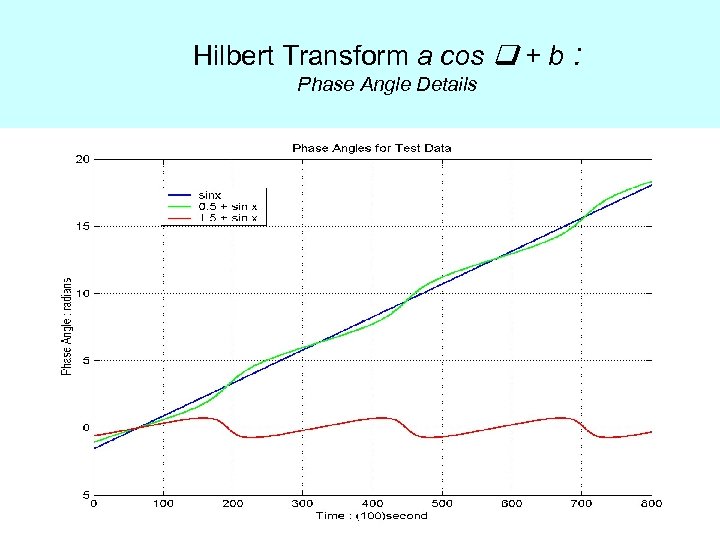
Hilbert Transform a cos + b : Phase Angle Details
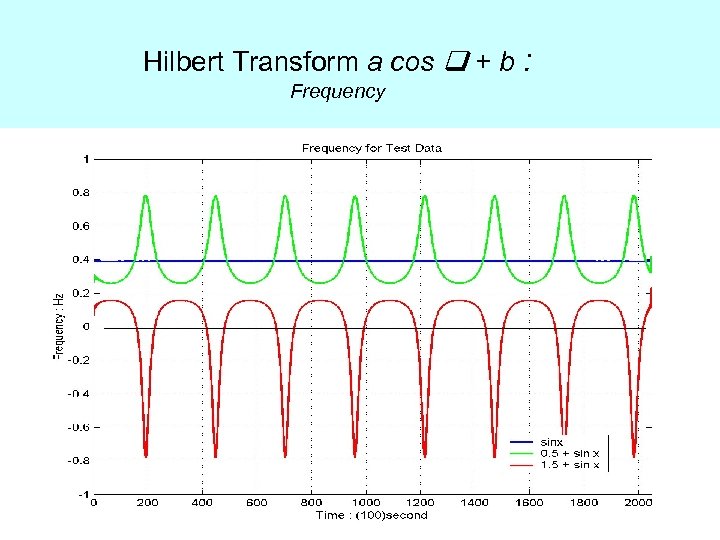
Hilbert Transform a cos + b : Frequency

The Empirical Mode Decomposition Method and Hilbert Spectral Analysis Sifting
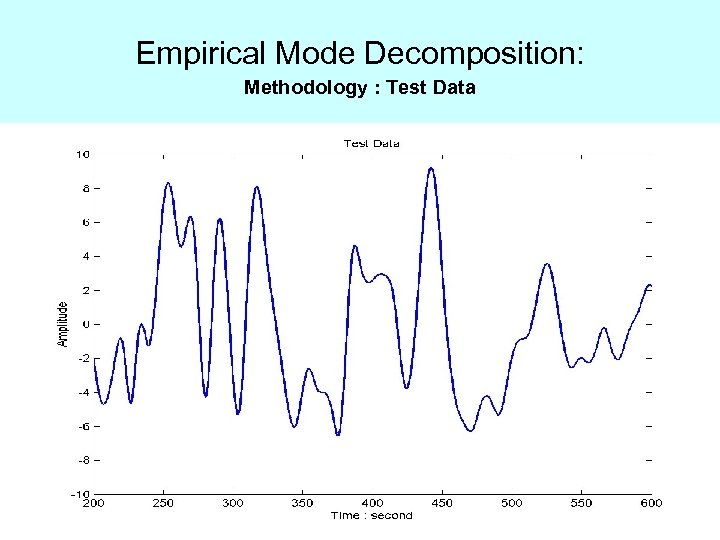
Empirical Mode Decomposition: Methodology : Test Data
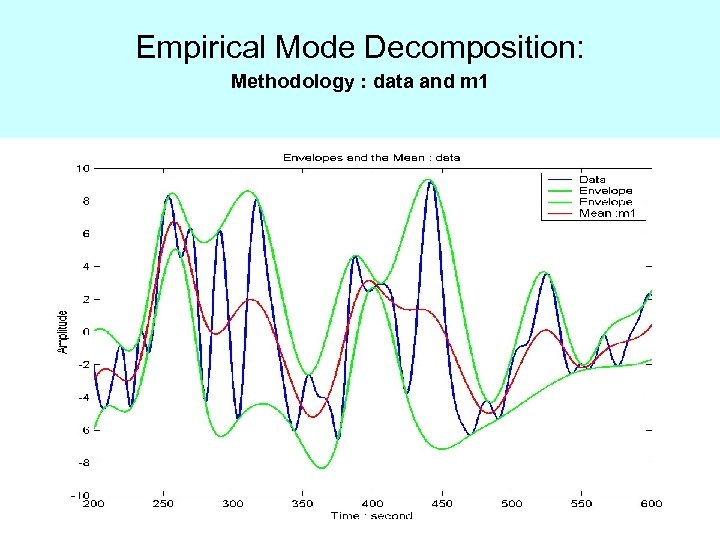
Empirical Mode Decomposition: Methodology : data and m 1
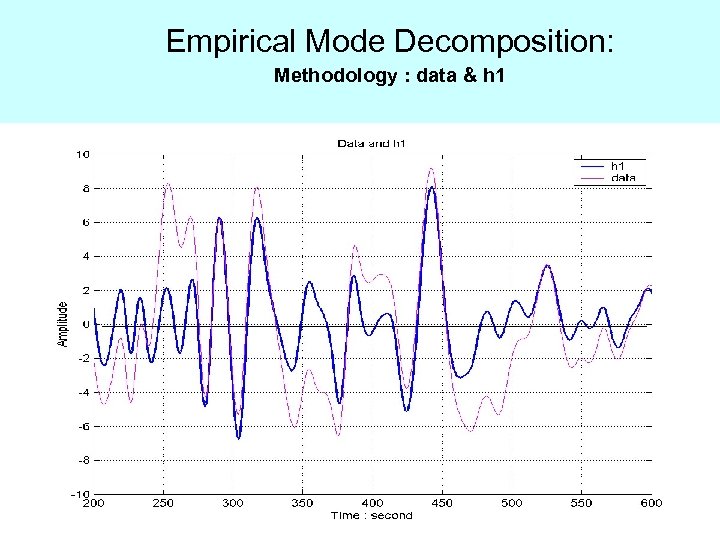
Empirical Mode Decomposition: Methodology : data & h 1
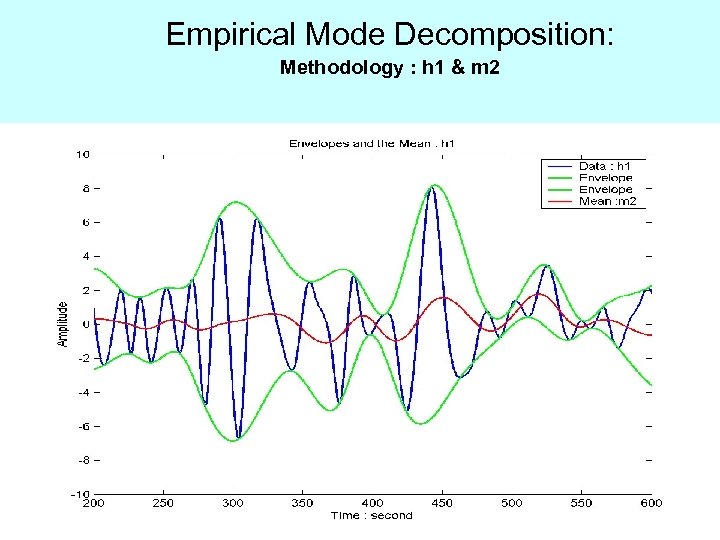
Empirical Mode Decomposition: Methodology : h 1 & m 2
Empirical Mode Decomposition: Methodology : h 3 & m 4
Empirical Mode Decomposition: Methodology : h 4 & m 5

Empirical Mode Decomposition Sifting : to get one IMF component

The Stoppage Criteria The Cauchy type criterion: when SD is small than a pre-set value, where
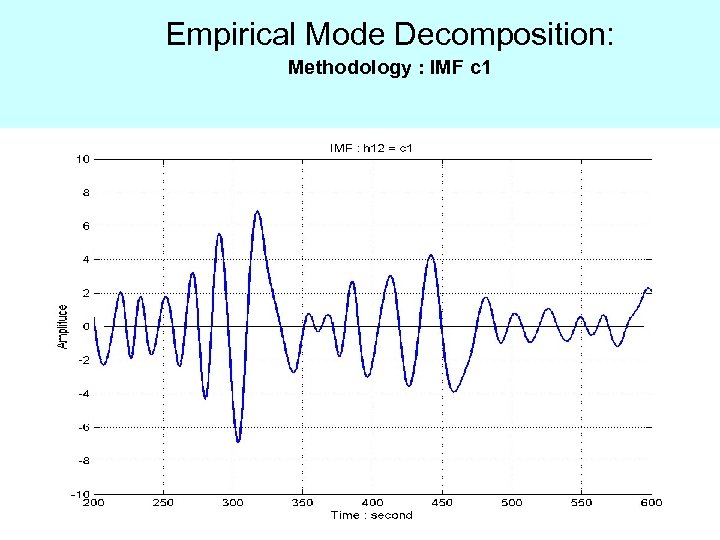
Empirical Mode Decomposition: Methodology : IMF c 1

Definition of the Intrinsic Mode Function (IMF)
Empirical Mode Decomposition: Methodology : data, r 1 and m 1

Empirical Mode Decomposition Sifting : to get all the IMF components

Definition of Instantaneous Frequency

Definition of Frequency Given the period of a wave as T ; the frequency is defined as

Instantaneous Frequency

The combination of Hilbert Spectral Analysis and Empirical Mode Decomposition is designated as HHT (HHT vs. FFT)

Jean-Baptiste-Joseph Fourier 1807 “On the Propagation of Heat in Solid Bodies” 1812 Grand Prize of Paris Institute “Théorie analytique de la chaleur” ‘. . . the manner in which the author arrives at these equations is not exempt of difficulties and that his analysis to integrate them still leaves something to be desired on the score of generality and even rigor. ’ 1817 Elected to Académie des Sciences 1822 Appointed as Secretary of Math Section 1823 paper published Fourier’s work is a great mathematical poem. Lord Kelvin

Comparison between FFT and HHT
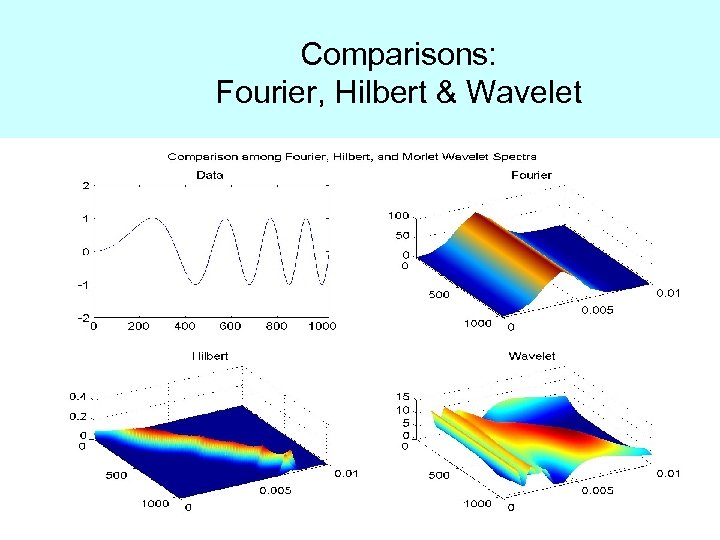
Comparisons: Fourier, Hilbert & Wavelet
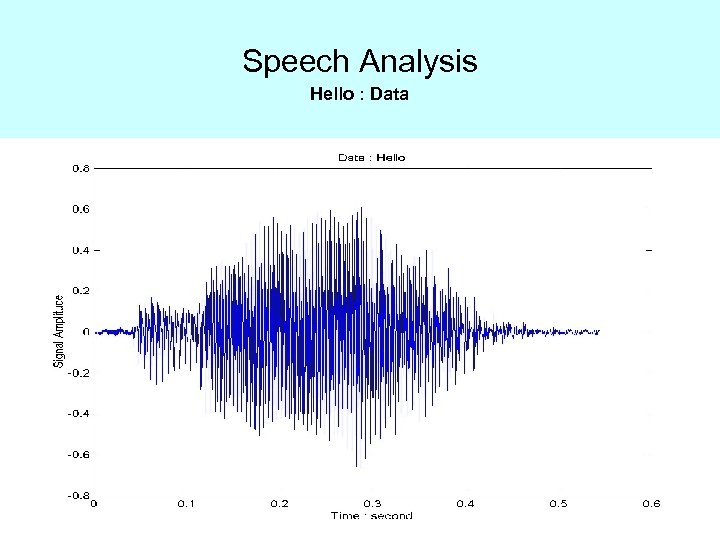
Speech Analysis Hello : Data
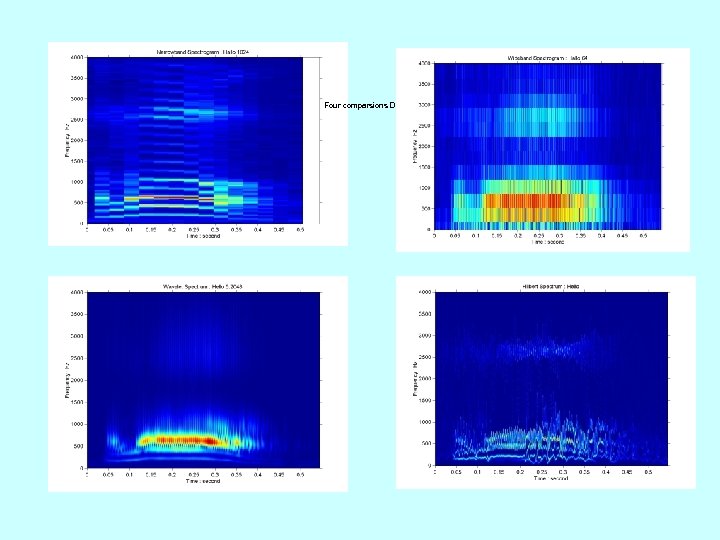
Four comparsions D

An Example of Sifting
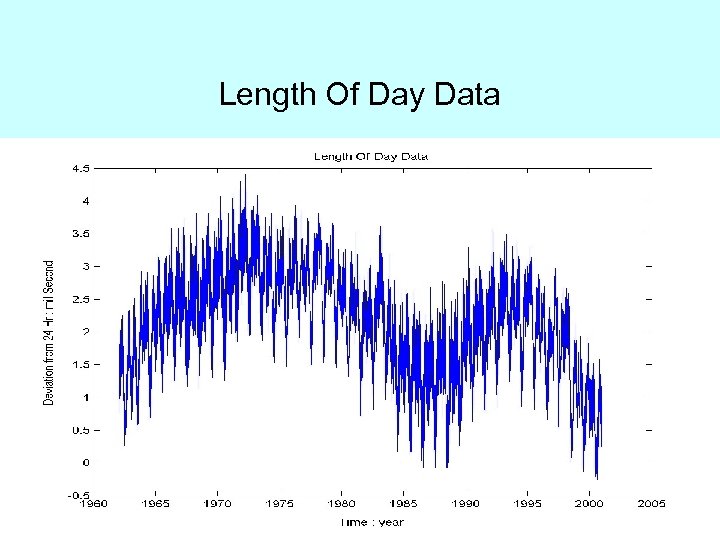
Length Of Day Data
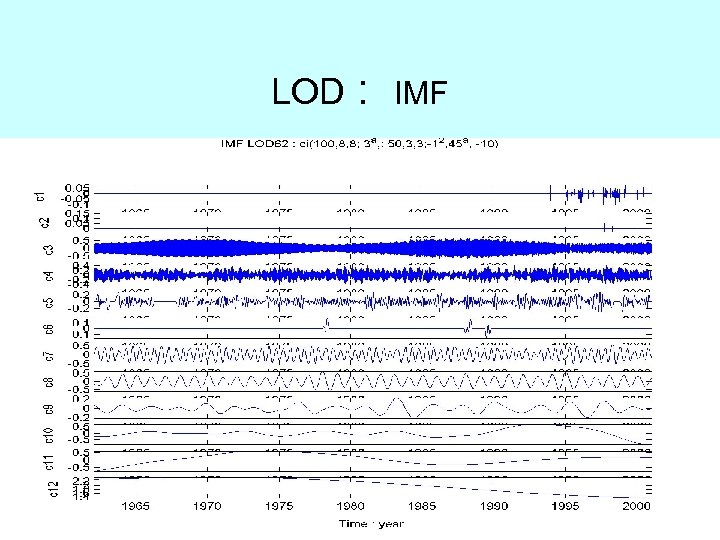
LOD : IMF

Orthogonality Check • Pair-wise % • Overall % • • • 0. 0003 0. 0001 0. 0215 0. 0117 0. 0022 0. 0031 0. 0026 0. 0083 0. 0042 0. 0369 0. 0400 • 0. 0452
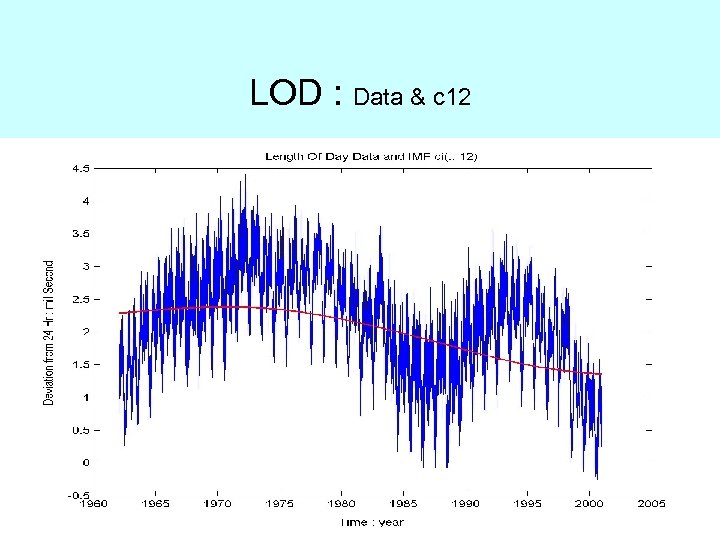
LOD : Data & c 12
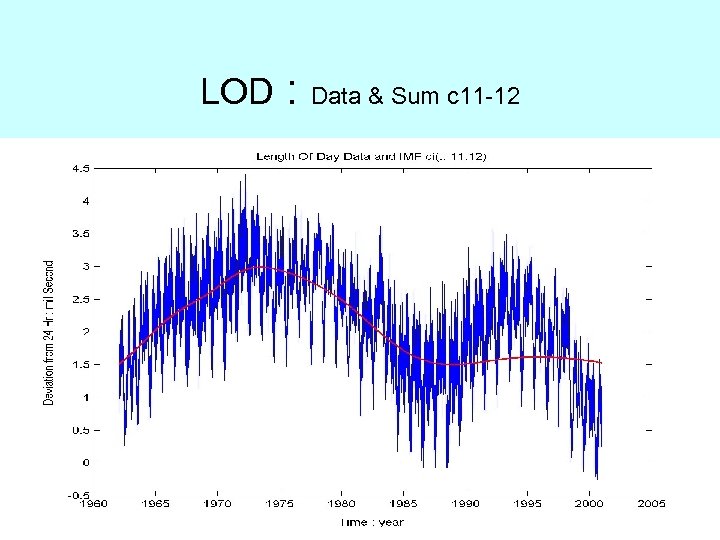
LOD : Data & Sum c 11 -12
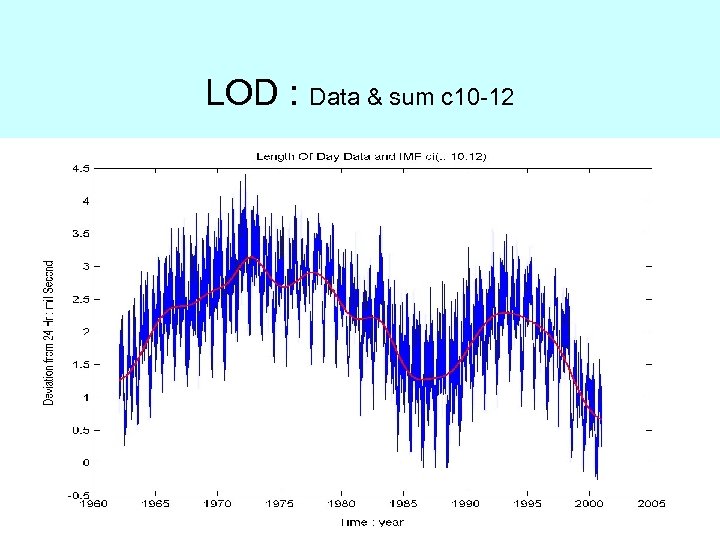
LOD : Data & sum c 10 -12
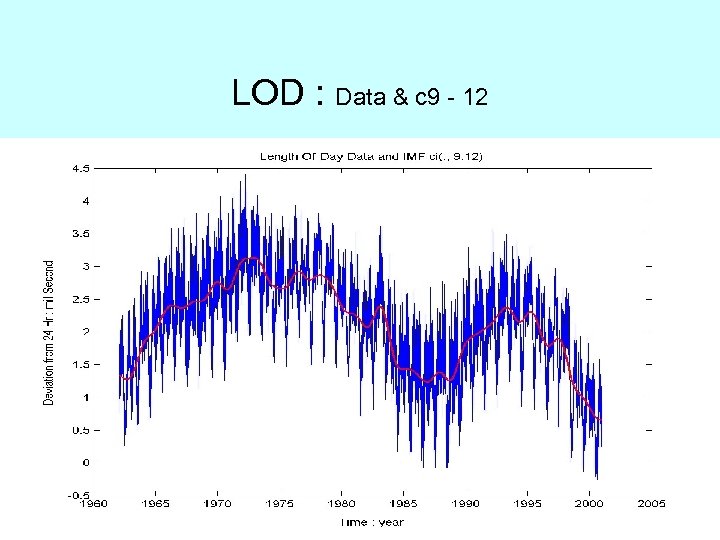
LOD : Data & c 9 - 12
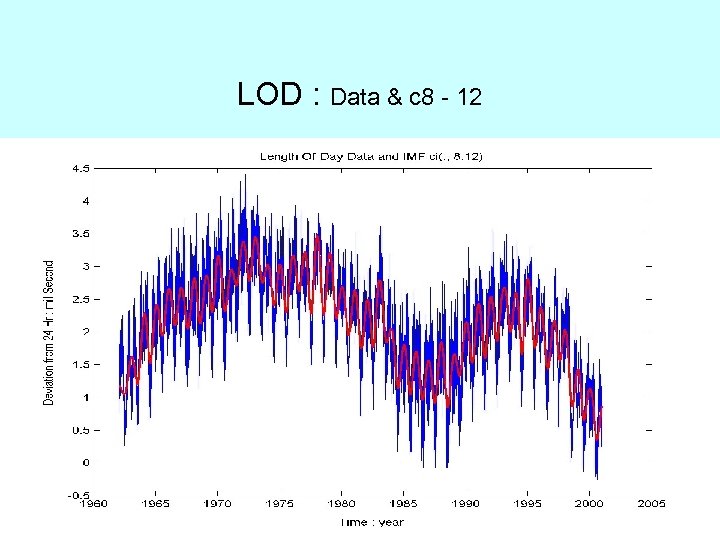
LOD : Data & c 8 - 12
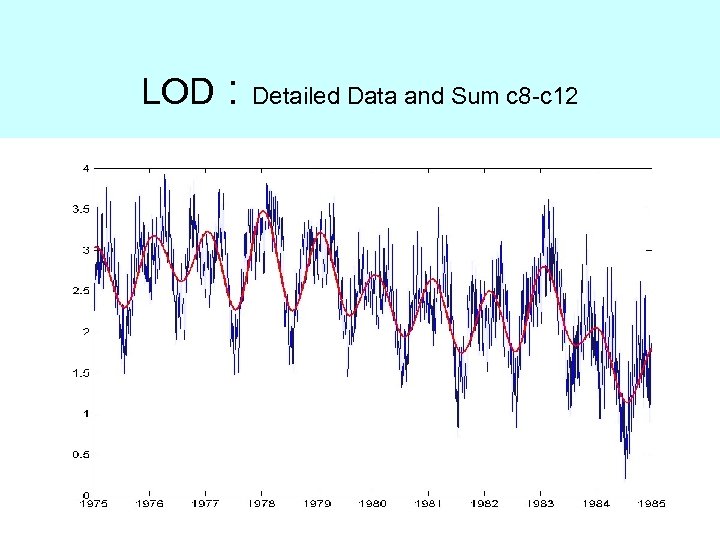
LOD : Detailed Data and Sum c 8 -c 12
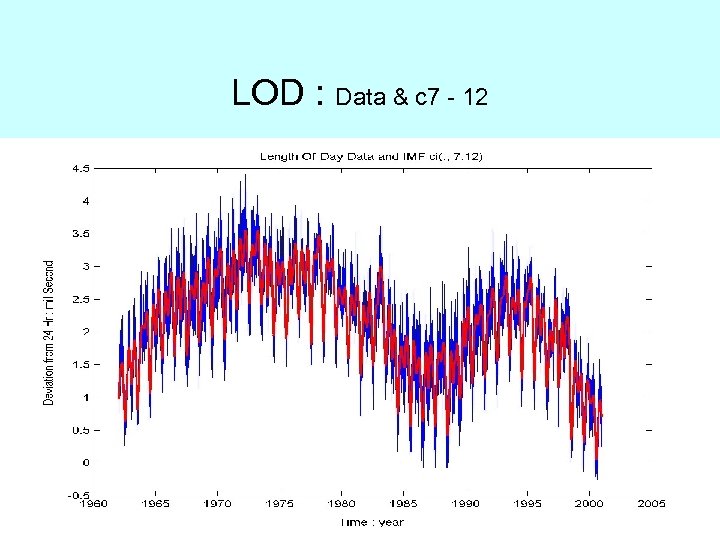
LOD : Data & c 7 - 12
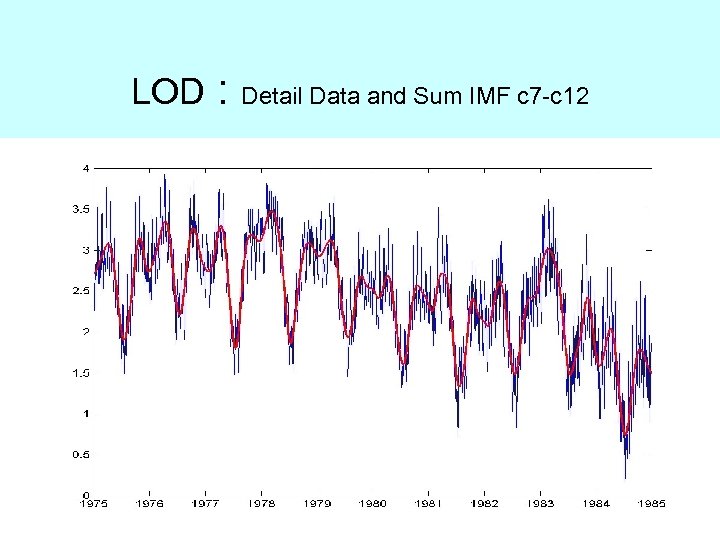
LOD : Detail Data and Sum IMF c 7 -c 12
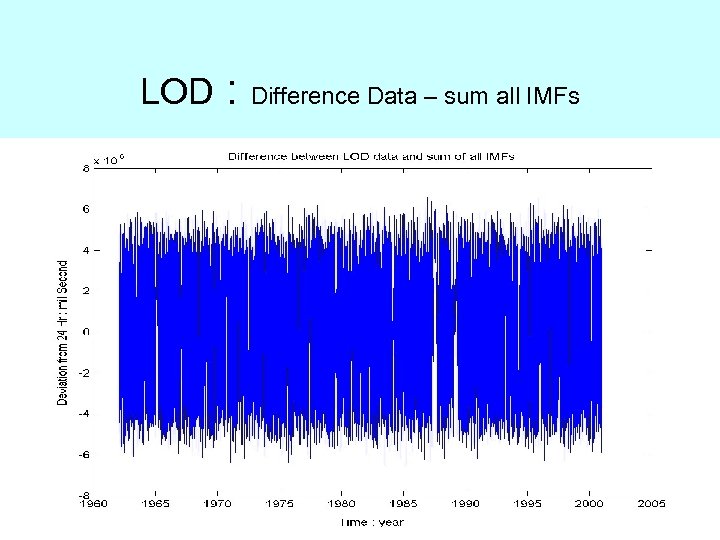
LOD : Difference Data – sum all IMFs
Traditional View a la Hahn (1995) : Hilbert
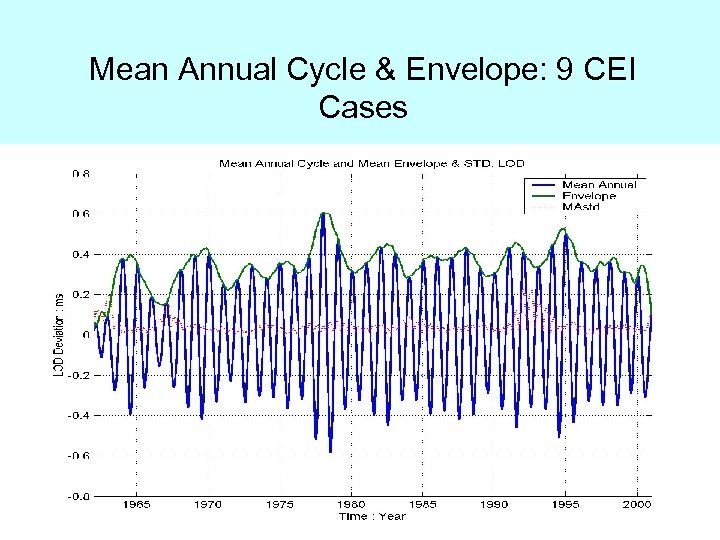
Mean Annual Cycle & Envelope: 9 CEI Cases

Properties of EMD Basis The Adaptive Basis based on and derived from the data by the empirical method satisfy nearly all the traditional requirements for basis a posteriori: Complete Convergent Orthogonal Unique

Hilbert’s View on Nonlinear Data

Duffing Equation
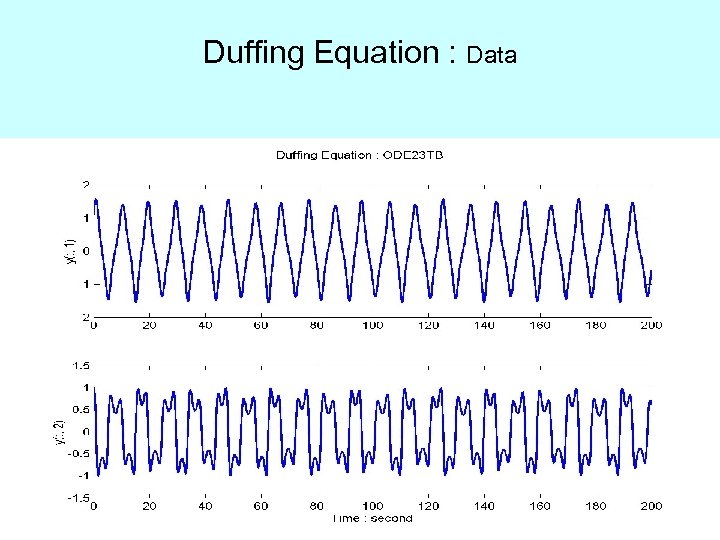
Duffing Equation : Data
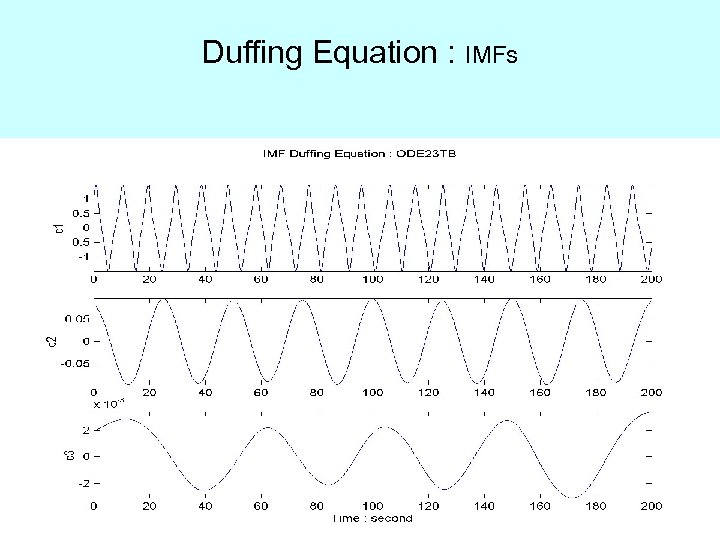
Duffing Equation : IMFs
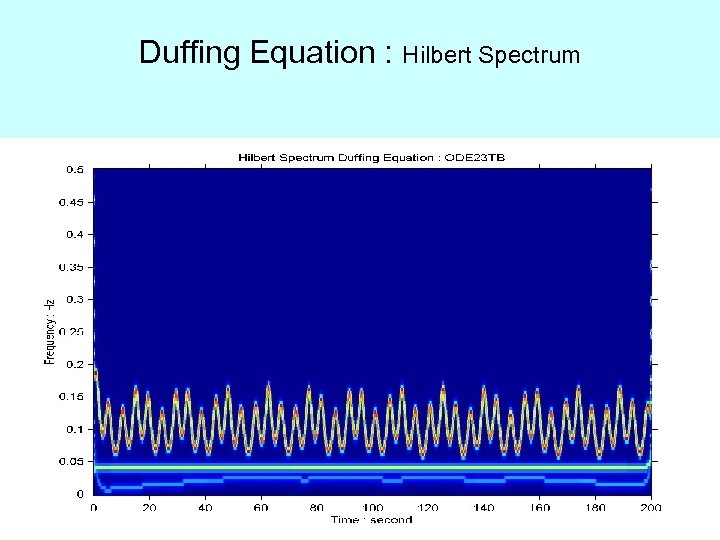
Duffing Equation : Hilbert Spectrum
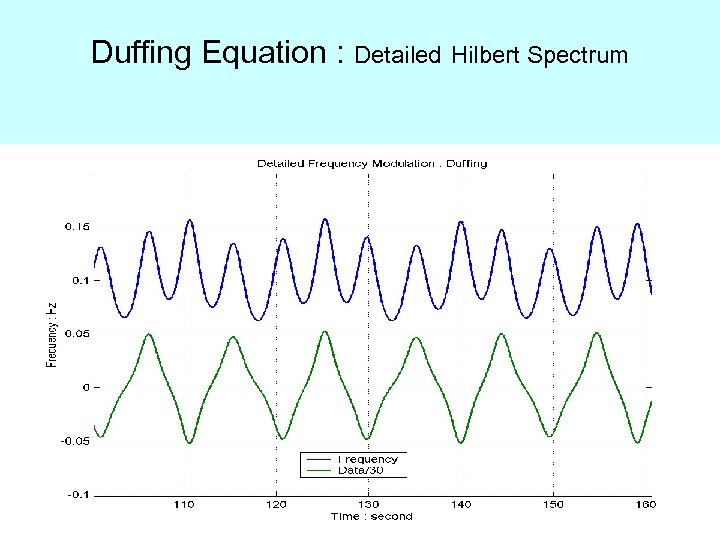
Duffing Equation : Detailed Hilbert Spectrum
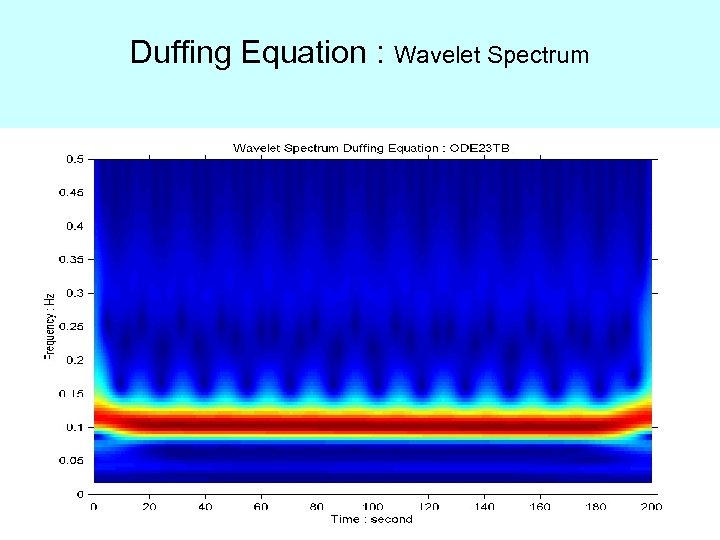
Duffing Equation : Wavelet Spectrum
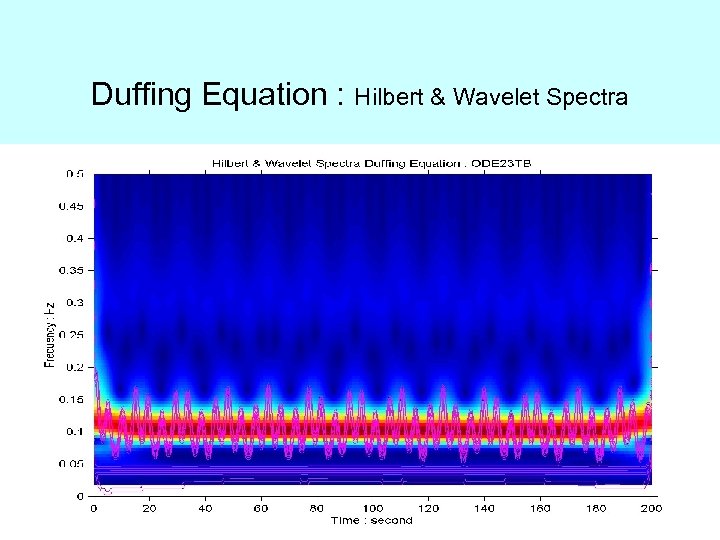
Duffing Equation : Hilbert & Wavelet Spectra

What This Means • Instantaneous Frequency offers a total different view for nonlinear data: instantaneous frequency with no need for harmonics and unlimited by uncertainty. • Adaptive basis is indispensable for nonstationary and nonlinear data analysis • HHT establishes a new paradigm of data analysis
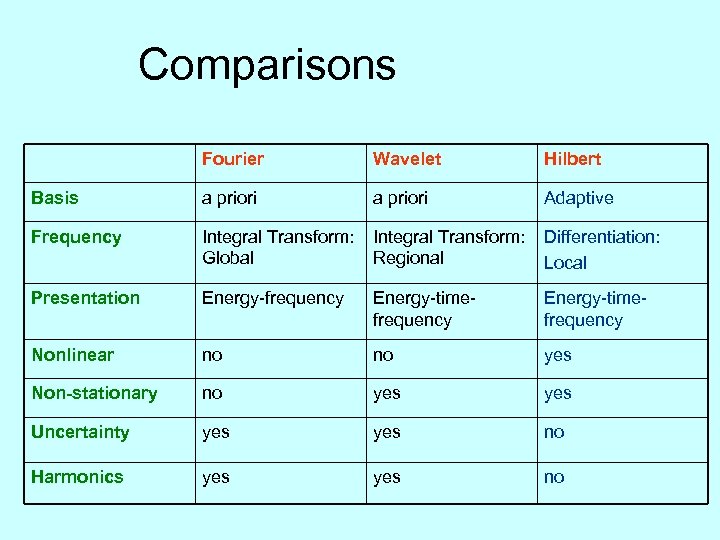
Comparisons Fourier Wavelet Hilbert Basis a priori Adaptive Frequency Integral Transform: Global Integral Transform: Regional Differentiation: Local Presentation Energy-frequency Energy-timefrequency Nonlinear no no yes Non-stationary no yes Uncertainty yes no Harmonics yes no

Application of Hilbert Huang Transform in Cerebral Blood Flow Regulation Multimodal pressure-flow method to assess dynamics of cerebral auto-regulation By Dr. Lo Meng-Yzung of RCADA, NCU and the Harvard Medical School, Division of Inter-disciplinary Medicine.
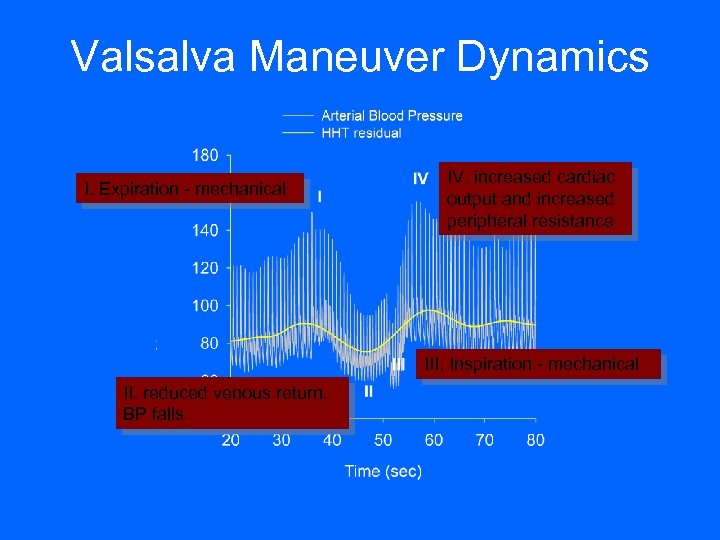
Valsalva Maneuver Dynamics I. Expiration - mechanical IV. increased cardiac output and increased peripheral resistance III. Inspiration - mechanical II. reduced venous return, BP falls
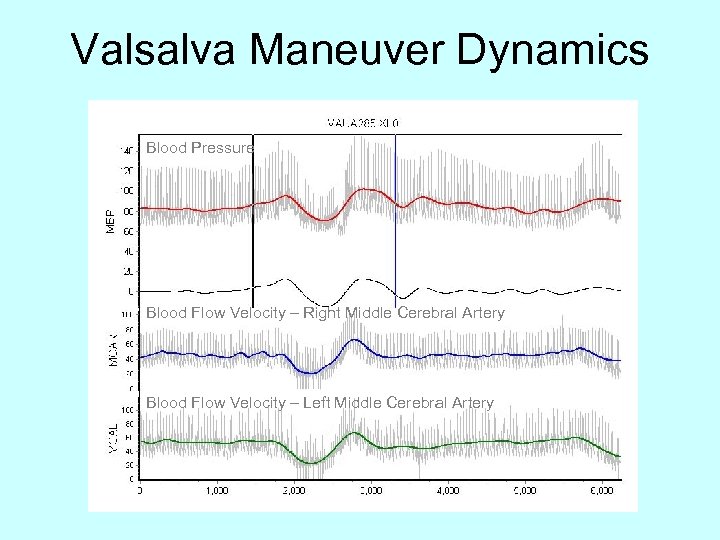
Valsalva Maneuver Dynamics Blood Pressure Blood Flow Velocity – Right Middle Cerebral Artery Blood Flow Velocity – Left Middle Cerebral Artery
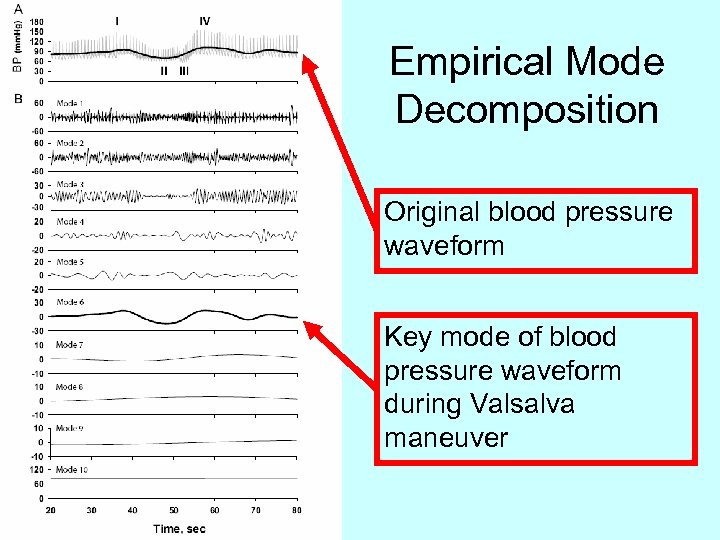
Empirical Mode Decomposition Original blood pressure waveform Key mode of blood pressure waveform during Valsalva maneuver
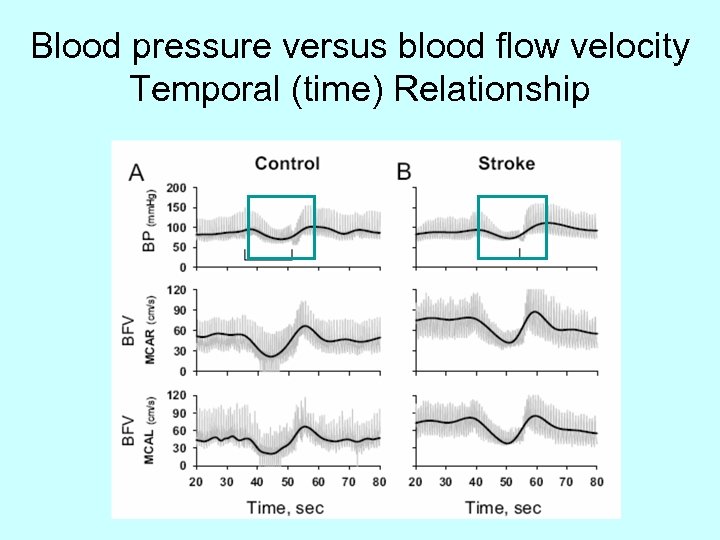
Blood pressure versus blood flow velocity Temporal (time) Relationship
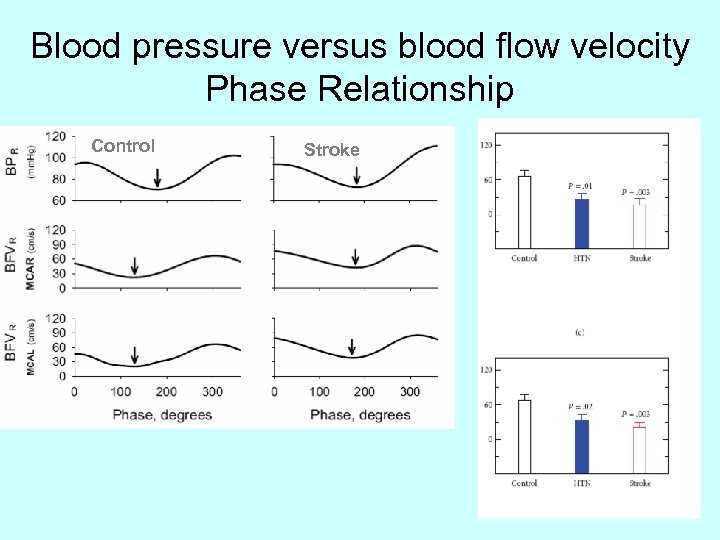
Blood pressure versus blood flow velocity Phase Relationship Control Stroke
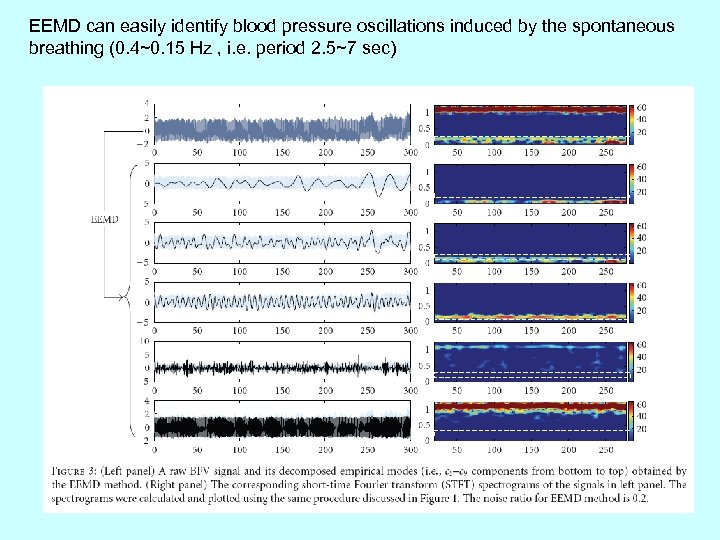
EEMD can easily identify blood pressure oscillations induced by the spontaneous breathing (0. 4~0. 15 Hz , i. e. period 2. 5~7 sec)
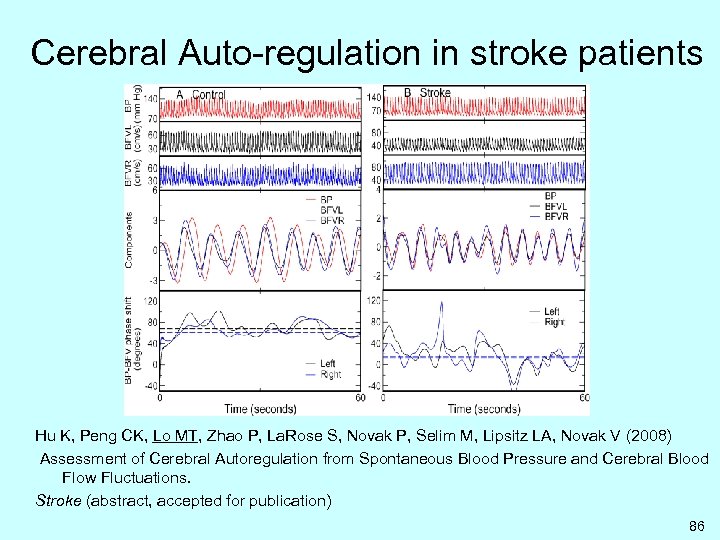
Cerebral Auto-regulation in stroke patients Hu K, Peng CK, Lo MT, Zhao P, La. Rose S, Novak P, Selim M, Lipsitz LA, Novak V (2008) Assessment of Cerebral Autoregulation from Spontaneous Blood Pressure and Cerebral Blood Flow Fluctuations. Stroke (abstract, accepted for publication) 86
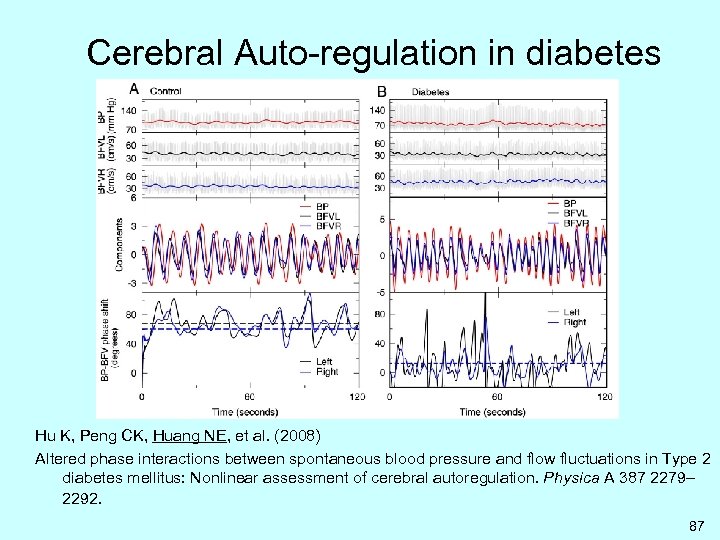
Cerebral Auto-regulation in diabetes Hu K, Peng CK, Huang NE, et al. (2008) Altered phase interactions between spontaneous blood pressure and flow fluctuations in Type 2 diabetes mellitus: Nonlinear assessment of cerebral autoregulation. Physica A 387 2279– 2292. 87
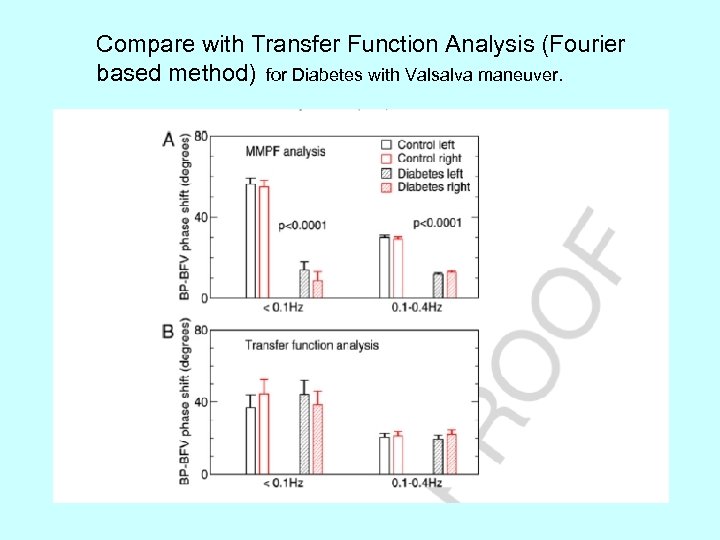
Compare with Transfer Function Analysis (Fourier based method) for Diabetes with Valsalva maneuver.
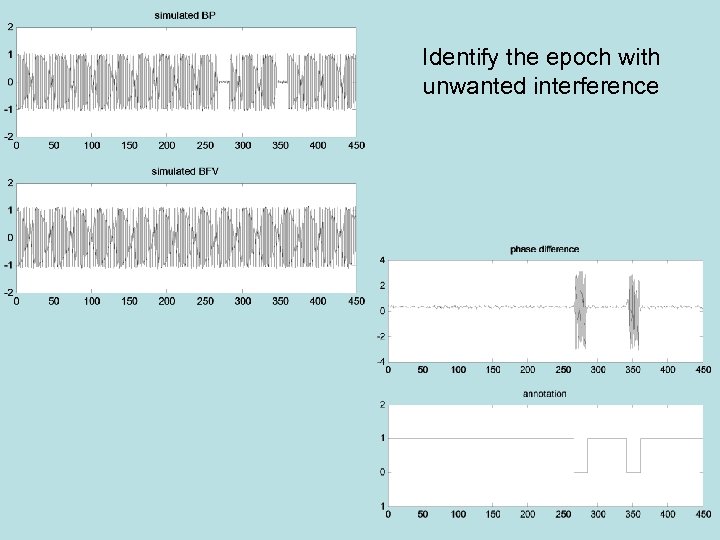
Identify the epoch with unwanted interference
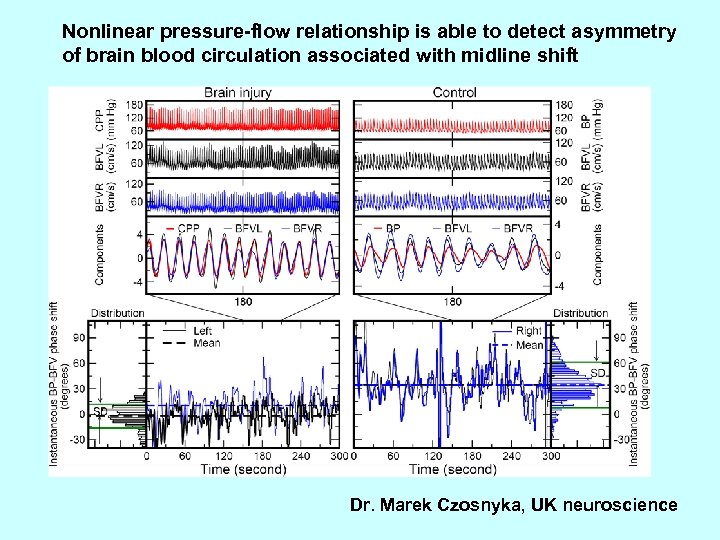
Nonlinear pressure-flow relationship is able to detect asymmetry of brain blood circulation associated with midline shift Dr. Marek Czosnyka, UK neuroscience
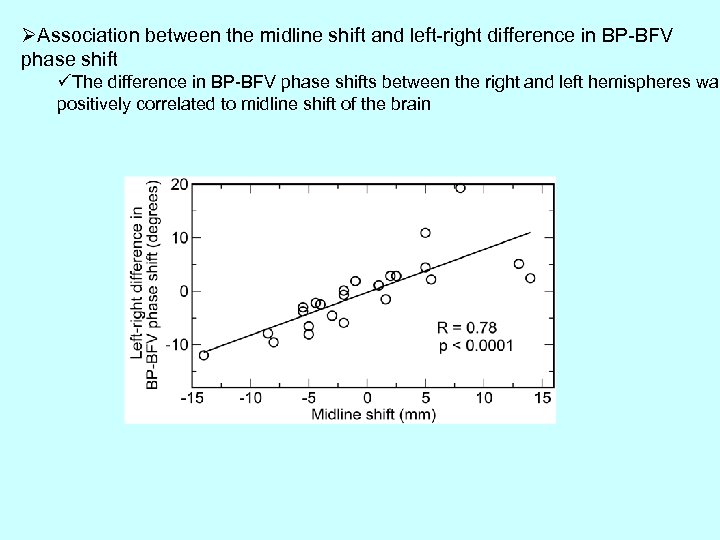
ØAssociation between the midline shift and left-right difference in BP-BFV phase shift üThe difference in BP-BFV phase shifts between the right and left hemispheres was positively correlated to midline shift of the brain

Image Analysis We have extended HHT to multi-dimensional data; A patent is being filed.
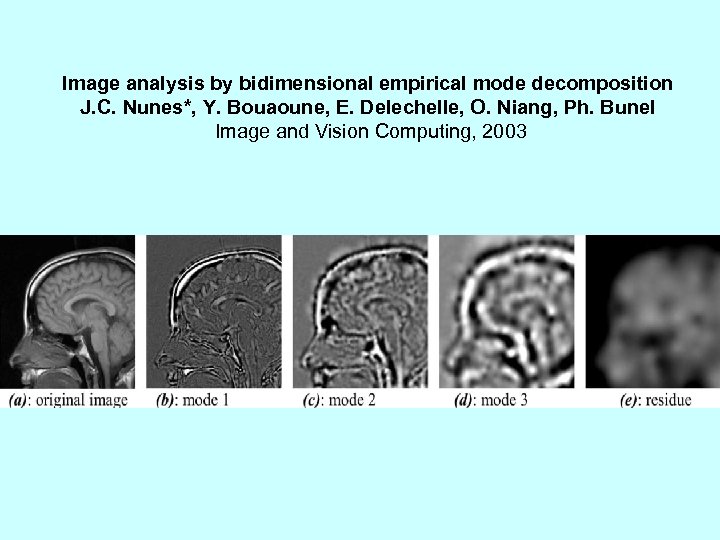
Image analysis by bidimensional empirical mode decomposition J. C. Nunes*, Y. Bouaoune, E. Delechelle, O. Niang, Ph. Bunel Image and Vision Computing, 2003


Conclusion Adaptive method is the only scientifically meaningful way to analyze data. It is the only way to find out the underlying physical processes; therefore, it is indispensable in scientific research. It is physical, direct, and simple. But, we have only started and what we have done is only a scratch of the surface.

Many of the most significant and interesting challenges of the modern world require boundary-crossing collaborations among scientists and scholars with widely different fields of expertise. Allison Richard Vice Chancellor, Cambridge University

Current Applications • • Non-destructive Evaluation for Structural Health Monitoring – (DOT, NSWC, and DFRC/NASA, KSC/NASA Shuttle) Vibration, speech, and acoustic signal analyses – (FBI, MIT, and DARPA) Earthquake Engineering – (DOT) Bio-medical applications – (Harvard, UCSD, Johns Hopkins) Global Primary Productivity Evolution map from Land. Sat data – (NASA Goddard, NOAA) Cosmological Gravity Wave – (NASA Goddard) Financial market data analysis – (NCU)

History of HHT 1998: The Empirical Mode Decomposition Method and the Hilbert Spectrum for Non -stationary Time Series Analysis, Proc. Roy. Soc. London, A 454, 903 -995. The invention of the basic method of EMD, and Hilbert transform for determining the Instantaneous Frequency and energy. 1999: A New View of Nonlinear Water Waves – The Hilbert Spectrum, Ann. Rev. Fluid Mech. 31, 417 -457. Introduction of the intermittence in decomposition. 2003: A confidence Limit for the Empirical mode decomposition and the Hilbert spectral analysis, Proc. of Roy. Soc. London, A 459, 2317 -2345. Establishment of a confidence limit without the ergodic assumption. 2004: A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method, Proc. Roy. Soc. London, A 460, 1597 -1611 Defined statistical significance and predictability. 2007: On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. , 104, 14, 889 -14, 894. The correct adaptive trend determination method 2009: On Ensemble Empirical Mode Decomposition. Advances in Adaptive Data Analysis 1, 1 -41. 2009: On instantaneous Frequency. Advances in Adaptive Data Analysis (Accepted)

Advances in Adaptive data Analysis: Theory and Applications A new journal to be published by the World Scientific Under the joint Co-Editor-in-Chief Norden E. Huang, RCADA NCU Thomas Yizhao Hou, CALTECH To be launched in the March 2008
f3fc52baff698605542a76e8268b8c36.ppt